统计力学视域下的量子理论发展
——从玻尔兹曼到普朗克
黄架栋
(上海交通大学科学史与科学文化研究院 上海 201100)
1 引言
路德维希·爱德华·玻尔兹曼(Ludwig Edward Boltzman)和马克斯·普朗克(Max Planck)同为19世纪至20世纪两大物理学家,在热力学、统计物理学、量子假说等领域作出了卓越贡献.玻尔兹曼提出的统计力学理论为热力学第二定律以及量子力学等理论的发展奠定基础.统计力学的简单描述,即可以通过构成宏观物质的微观原子的属性来预测和判断宏观物质的物理性质.玻尔兹曼统计是全同粒子的经典统计法,其描述了热平衡中不相互作用的材料颗粒在各能态下的平均分布,适用于当满足温度足够高或颗粒密度足够低时量子效应可忽略的情况[1].此外,玻尔兹曼建立了玻尔兹曼方程用以描述气体从非平衡态到平衡态的变化过程,在这之后他提出了著名的玻尔兹曼熵公式[2].普朗克早期主要从事物质的聚集态变化、气体等范围内的热力学研究,之后也参与到热辐射的研究中,一些物理学家试图用合适的公式来解释黑体辐射实验时,他们发现瑞利—金斯公式和维恩位移定律均不符合实验结果,在已有研究上,普朗克于1900年提出了最符合实验结果的公式,即普朗克辐射公式,并在德国物理学年会上作了汇报,他认为要获取同实验数据匹配的能量公式,必须假定能量的吸收或辐射不是连续进行的,而是分段进行,且只能取其中某个最小能量值的整数倍,而这个最小值被称之为能量子[3].如果将辐射频率设为ν,可得到最小数值ε=hν,其中h被称为普朗克常数.在黑体辐射的基础之上,普朗克总结了能量量子化概念,如果一个物体中的宏观物理量可以最小单位(能量子)作非连续的跳跃式增减,那么就可称此宏观物理量是符合量子化的.
2 玻尔兹曼及其统计力学
玻尔兹曼是奥地利著名物理学家,同时也是热力学和统计力学的主要奠基人之一,1863年开始在维也纳大学学习物理学,1866年获得理学博士学位之后在多所大学担任过教授,后于1899年评选为英国皇家学会会员.1866年,英国物理学家麦克斯韦(James Clerk Maxwell)提出了麦克斯韦分布律用以测算分子的运动速率,玻尔兹曼将分布律延伸至分子在任一力场中的运动情况,由此得出了在有势力场中,如果分子处于热平衡状态之下,分子之间能够按照能量大小的标准来排布的规律,这一规律被称之为玻尔兹曼分布律,并进一步得出若分子为气体分子,且处于重力场的条件之下,那么其中的气体分子能够按照高度进行分布的规律[4].玻尔兹曼在气体分子从非平衡态到平衡态进行过度这一研究基础上建立起玻尔兹曼积分微分方程,即由分子速度分布函数f定义一个泛函数H,需要证明当分子速度分布函数f发生变化时,定义的泛函数H会随着时间的增加而单调地减少,当泛函数H减少到最小值时,系统刚好到达一个平衡状态,这就是著名的H定理[5].H定理代表了系统中的一种平衡状态的变化,也就是说在热力学过程中,气体从非平衡态向平衡态转变过程的不可逆性.玻尔兹曼的统计概念由此开始逐渐成熟起来.
在给出了H定理的证明之后,玻尔兹曼引入了熵和热力学定律的关系式用以系统解释热力学第二定律,熵函数S可以跟logW成正比.但这一非平衡态向平衡态转变过程中的不可逆性出现了矛盾,当系统中分子数量较多时,大量的分子在相互作用中表现出来的宏观热力学过程确实符合上述所讲的H定理系统中的平衡状态,在这一平衡过程中H函数表现为单调减少而熵函数S表现为单调增加,但如果从微观层面看单个分子的运动却是可逆的,因此宏观和微观上两种完全矛盾的结果为当时的物理学家们感到困惑,但这一矛盾为玻尔兹曼完善统计概念提供了契机.1877年玻尔兹曼发表了题为《论热力学第二定律与几率的关系,或平衡定律》的论文.在这一篇论文中,玻尔兹曼通过概率推算,将熵S和整个热力学系统中产生此矛盾的概率联系在一起,得出了S∝logW这一结论,随后1900年普朗克将这一结论继续演变,最终得出公式S=klnW,这一公式更清楚表示在一定概率情况下两者之间的正比关系,公式中的k被称之为玻尔兹曼常数[6].这也是历史上第一次提出整个系统中的宏观态和其本身的微观态的对数形成正比这一结论,这一正比规律完美解决了宏观态和微观态之间的矛盾问题,也解释了热力学第二定律中的统计概念的含义.在热力学系统中,确实有可能存在与非平衡态向平衡态转变相反的矛盾情况,也就是H函数在自发增大或熵S在自发减小,但这种可能性从上述公式来看,几率非常小.这种统计概念将热力学过程的不可逆性和力学过程的可逆性完美结合在一起,它揭示了热力学的过程实际是物质内部各个分子运动的结果,其结果所反映的统计规律性是由数量相当庞大的分子作统一运动产生的,气体运动理论和统计力学之间存在密切的联系.此外,为进一步完善热力学理论中的统计概念,玻尔兹曼将其与麦克斯韦电磁场理论相结合,具体应用于黑体辐射理论的研究中.
3 普朗克及其量子假说
普朗克1858年出生于德国,1874年进入慕尼黑大学学习数学和物理专业,后又转入柏林大学专攻物理学,1879年获得博士学位以后随即提出了热力学第二定律的普朗克说法.普朗克在其他物理学家的理论基础之上,对于量子和能量问题进行了更深入的系统研究,而后在1900年的德国柏林物理学年会上,他提出了一个具有革命意义的假说,即现在非常著名的普朗克量子假说——每一个自然频率为ν的线性谐振子,只能够不连续地吸收或释放能量,其能量值必须是某一最小能量子的整数倍[7].普朗克认为,即使此假说可能存在正确性,但是在对待像能量、量子等这些基础但又新颖的概念时,必须要谨慎起见,尽量采取谨慎保守的研究态度.普朗克编写的《热力学讲义》是他的热力学成果汇总,他在仔细研究了热力学的不可逆过程之后提出自己对热力学第二定律的看法,其著作很快就成为热力学理论的权威,其中的理论假说和公式与不少物理学家的热力学思想不谋而合,虽然这时普朗克对热力学理论中的能量传递连续性观念丝毫不存怀疑,但他的看法很快就会被自己提出的量子假说改变[8].
普朗克的量子假说源于对热辐射问题中的黑体模型研究,指黑体将射入自身的辐射全部吸收,不存在反射也不存在透射,黑体自身辐射出的能谱与黑体自身外形无关,只与自身温度相关,但物理学家们在研究中发现,先前得到的各种辐射公式,都会推导出波长越短,热辐射强度越大,并且随着波长越来越短,热辐射强度会无限制增大的结论,这个巨大的理论错误被称为“紫外灾难”[9].普朗克在此基础上提出了能量量子化假说,亦可称之为能量分立思想,才能消除“紫外灾难”.普朗克提出的能量分立理论在当时的物理学界引起了较大的轰动,也招来了大量的反对.由于经典物理学在牛顿力学之后的思想烘托下,自然过程连续观念已经在科学家心中根深蒂固,无论是力量传递亦或是能量流动,在物理学家眼中都是连续进行的,因此普朗克提出的这一分立假设无异于从根深蒂固的观点上反对经典物理学,以普朗克为代表的量子力学拥护者受到了一系列经典物理学家一阵阵的反对浪潮,虽然在面对“紫外灾难”时普朗克的量子假说更能解决实际问题,但由于观点的格格不入导致当时的物理学家只接受这一假说对问题解决的实效性,但不接受这一理论假说本身,因此普朗克的理论在一段时间内遭到冷落.此外矛盾的是,对普朗克自身而言,他接受了一套系统性完整的经典物理学的培养模式,因此在争端产生以后,普朗克一度想让自己的假说进入到经典物理学的范畴,通过经典物理学来证明假说的合理性,但最终无果.普朗克甚至想放弃量子假说,重新利用经典物理学的理论来解决黑体实验中出现的“紫外灾难”问题,然而事实证明经典物理学已具有其一定的局限性,因此普朗克的努力遭遇了一系列的失败,最终以无果收尾.在这一阶段中,普朗克对自己的理论存在一种矛盾心态,他不得不承认量子理论似乎正在逐渐占据上风,但是由于他依然坚信经典物理学的权威,所以在假说之后,普朗克其实并没有在量子力学领域作出更进一步的研究以及更大的贡献,但随着理论的不断更新,量子力学迅猛发展,拥护者人数逐渐庞大,普朗克才慢慢接受自己提出的量子理论.
4 黑体辐射及量子理论
玻尔兹曼统计力学来源于对麦克斯韦速率分布律的推导.麦克斯韦速率分布律为
将公式变形,也能写成
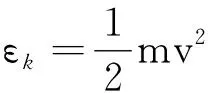
关于黑体辐射现象的研究,1859年德国物理学家基尔霍夫(Gustav Robert Kirchhoff)首次发现在热平衡状态下的封闭空腔内,物体能量的辐射和吸收之比只取决于温度和波长,与制造这个封闭空腔本身的材料无关,由此得到基尔霍夫辐射定律.1879年玻尔兹曼同斯特藩(Stefan Josef)合作,得到黑体总辐射能与绝对温度的4次方成正比的结论,该结论被称为斯特藩-玻尔兹曼定律[11].1896年,维恩(Wilhelm Wien)根据辐射能量的分布和分子运动的速率,结合麦克斯韦速率分布律得到他的辐射公式,但此公式实际是缺乏实验根据的,因此当卢默尔(Otto Lummer)和德国数学家普林斯海姆(Ernst Pringsheim)在1899年验证维恩辐射公式时发现当红外线测量范围扩大到18 μm辐射值的范围,只有满足波长较短,温度较低的情况,维恩辐射定律才能与实验结果相符合,而在长波区域公式计算的数值要小于实验获得的实际数值[12].不过维恩的黑体辐射定律在没有进一步研究前一直被看作是大致符合实验数据的标准.英国物理学家瑞利(Rayleigh)也推导出一个黑体辐射定律,随后由英国数学家金斯(James Hopwood Jeans)修正公式中错误因子,因此这个公式又称瑞利-金斯辐射定律,但这个公式造成了“紫外灾难”,即随着辐射频率的单调增加,高频部分的能量辐射会趋于无限大,并在紫外端发散.普朗克在维恩的基础上,认为应该将熵的概念运用到公式推导中,如果将振子的熵和整个空腔内的其他平均辐射能量联系起来,就可以推出黑体辐射的公式,从而得到黑体辐射的能量规律.1899年,普朗克进一步定义振子熵和平均能量间的关系并结合玻尔兹曼的统计思想最终得到普朗克黑体辐射公式.
普朗克发现一旦物体的辐射温度逐渐升高,单色辐射的强度与温度成正比,这说明振子的平均能量和温度之间成正比关系[13].普朗克在此基础上根据热力学第二定律推导出一个关系式,再将此公式和维恩位移定律相结合,得到两者之间的正比关系,最终普朗克推导出新的黑体辐射公式
从普朗克黑体辐射公式可知,在高频条件下辐射波长变短时,可以转化为维恩公式,而在低频条件下辐射波长变长时,转化为瑞利-金斯公式,因此这个公式完全符合在任一条件下的实验结果[14].但是普朗克也意识到,这个公式的成功并非偶然,其中还有必然的因果联系,因此他决定向这一难题发起挑战,除保护热力学的基本定理以及新推导的公式外,还可能会对经典物理学的权威发起质疑,因此普朗克面临着巨大的压力.
普朗克在诺贝尔物理学奖颁奖演说中提到,从这个公式出现起,他就开始承担寻找其中必然性的任务,由于受到玻尔兹曼的统计力学和概率思路的影响,他开始研究熵和概率之间的关系.普朗克根据玻尔兹曼提出的一个适用于任一物理形态的具有普遍意义的表达式,即S=klnW,表达式中的W是对应状态下的热力学概率,普朗克假设一个辐射空腔内有一定数目的赫兹振子,这些赫兹振子相对应于一定的频率,同时这些赫兹振子还拥有总的能量值,现在需要确定的是这些振子的总能量一共有多少种可能的分配方式,也就是公式中的W,热力学的概率的数值是多少,这就要求不能将振子总能量看作是一个可以被无限分割的量,而是要将其作为一个有限数量的多个相同部分的共同组成,例如将总的能量划分为一定份数的P,这几份总能量P能够在一定数量的振子中按照不同比例分配给每个振子,这几种不同分配比例代表的不同分配方法就是公式中W的量,因此就可以得到P在一定数目振子中可以形成的容配比,最终普朗克根据玻尔兹曼的统计规律得到上述黑体辐射公式.
普朗克在1900年12月14日的德国物理学年会上以《正常光谱辐射能的分布理论》为题作了论文汇报,同时他在解释新的黑体辐射公式时认为,能量在传递过程中并不是连续的,而是通过量子的形式不断释放出来,是分立化的,并且量子携带的能量只取决于频率大小,这就是后来量子物理中所说的能量子,其能量值为普朗克常量与频率的乘积,即ε=hν.
普朗克将正确的黑体辐射公式带到大众面前,也使得能量理论从经典物理学中的连续性向量子化时代转变,因此1900年12月14日这天被认为是“量子力学诞生日”.
5 结束语
普朗克能够利用玻尔兹曼的统计方法推导出黑体辐射公式,这与玻尔兹曼的统计力学规律具有的普遍适用性是分不开的.S=klnW这一公式使得物理学理论第一次用概率的形式表达出来,以此相对的似乎只有牛顿的运动定律和爱因斯坦的质能关系[15].
在玻尔兹曼的统计公式中,常数k具有自然原则,遵循自然界的统计规律,将宏观物体和微观量子通过概率联系在一起.玻尔兹曼的统计规律是具有广义性的,不管是微观意义上的分子运动规律,亦或是宏观物体的运动规律,还是人类社会以及动物族群等运动规律,无一不受其支配,它囊括了自然运动的规律和社会科学的规律甚至宇宙运动的规律,同时也关乎于热力学领域和非热力学领域.要注意的是,这个规律不适用于单一物体,只有当大量物体在同一容器内运动的情况下,此时研究单一物体的运动才能显现出规律,通过微观运动来解释宏观现象.当一个宏观系统内部出现差异量时,这种差异量可以用公式中的W来表示,他代表系统内部存在一定差异性.正是因为玻尔兹曼统计力学具有的普适性,才使熵这一概念持续扩大化,S=klnW这一公式成为大部分熵公式的基础,衍生至各个领域.因此当普朗克进一步完善黑体辐射定律时,他考虑到了玻尔兹曼的统计公式,并将其应用到整个宏观空腔中的辐射能量产生的微观粒子运动层面,通过分析概率得到能量是以量子形态进行放射吸收这一全新结论,开创了物理学量子化的新时代.

