基于统计抽样原理的典型室温分布比例确定方法研究

马立新 李 彪 李少武 齐吉星 齐承英 顾吉浩

(1.天津华电福源热电有限公司,天津;2.工大科雅(天津)能源科技有限公司,天津;3.河北工业大学,天津)

0 引言

集中供热行业存在较大的节碳空间,能源转型和节能降耗是实现集中供热行业“双碳”目标的有效途径。截止到2020年底,全国集中供热面积为123亿m2,较2019年增长了7.8亿m2,增长率为6.8%[1]。庞大的能源消耗给我国的能源供给与节能减排带来了艰巨的挑战,国家能源局发布的《能源生产和消费革命战略(2016—2030)》中明确指出应建设互联网+智慧能源,促进能源与现代信息技术深度融合,推动能源生产管理和营销模式变革。城镇供热行业作为重要的能源消耗行业,应响应国家号召,做出重要革新[2]。在各项科学技术的加持下,全面实现智慧供热已成为供热行业发展的趋势。在智慧供热系统建设中,用户室温是实现按需供热、精准供热的一个关键参数。建设典型用户的室温采集系统,实时了解用户室内供热状态,对合理分配供热资源、满足用户日益精细化的供热需求具有重要意义。

近年来,不少学者对室温采集系统的设计与应用等进行了深度研究。王亚楠等人研发的智慧供热平台将热用户室温数据在线同步上传,可以直观查看热用户室温变化,评判供热效果[3]。于春来等人研发了适合我国集中供热的楼宇室温监测装置及系统软件,实现了楼宇室温的自动监测[4]。刘志新等人对当前主流室温采集设备进行了对比分析,并选用适合的设备应用到企业智慧供热平台中,为智慧供热技术的成功应用提供了数据支撑[5]。程雪进行了实地室内热环境测量并分析了影响因素,对比了基于不同的机器学习方法建立的室温测量模型,给出了合理的室温测量模型[6]。Essien等人对数据记录仪在建筑室内外温度监测中的应用进行了分析[7]。Wilby等人通过观测低收入城市社区极端室内温度,使用多个温度指标和分层分析评估了各影响因素下的室内温度变化[8]。Chen等人提出了一种利用无线网络传感器进行室内温度监测的方法[9]。

综上,目前国内缺乏与典型室温分布比例确定方法相关的文献。本文以河南濮阳某小区的室温采集系统为研究对象,基于统计抽样原理,进行室温抽样推断,对比分析不同抽样方法及不同抽样比例的统计结果,为典型室温分布比例的确定提供理论依据。

1 项目概况

1.1 研究对象

以河南濮阳某小区为例,该小区一共5 194户,其中4 076户安装了室温采集装置,安装比例为78%。累计设置3 825个室温采集点,通过上位机软件平台获取了2022年2月18日11:00的室温即时数据。理论上当样本量足够大时,室温抽样分布符合大数定理和中心极限定理。该小区停热用户较多且存在水力不均衡现象,剔除非供暖用户及[16 ℃,26 ℃]区间以外异常室温数据后,剩余2 426 个有效室温数据。经过K-S检验,2 426个有效室温样本的显著性差异值P=0.208,大于0.05,说明样本服从正态分布的假设成立。图1显示了室温分布统计结果。

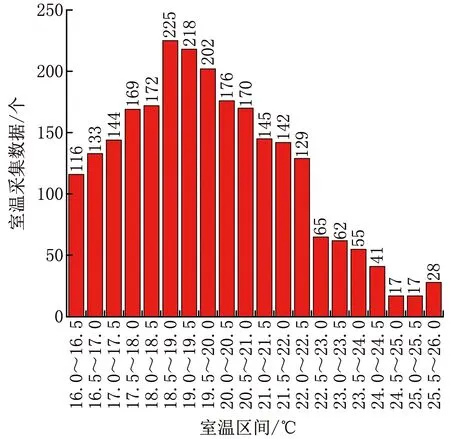
图1 小区室温分布统计结果

1.2 样本分类

小区分3期建设,共107栋建筑,1期21栋,2期65栋,3期21栋。根据建筑距离热力站的远近进行划分,位于供热系统前端、中端和末端建筑的比例为1∶3∶1。根据热用户在建筑中所处位置的不同,可以分为边角、边户、顶中、中间与底中用户,见图2。根据图2中的分类原则,6层建筑的边角、边户、顶中、中间、底中的用户比例为1∶2∶1∶4∶1,11层建筑的边角、边户、顶中、中间、底中的用户比例为2∶9∶1∶9∶1。

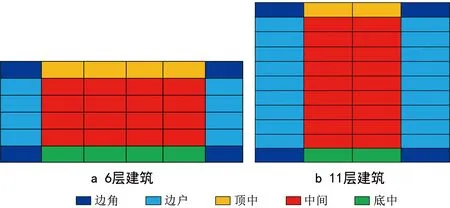
图2 热用户分类

根据上述分类原则,小区热用户的分类结果统计如表1所示。

2 方法原理

2.1 抽样方法

常用抽样方法包括随机抽样、分层抽样、整群抽样、系统抽样。在抽样统计中,很少单独采用随机抽样方法,常将2种或几种抽样方法结合使用。

1) 整群抽样:将总体划分为若干群,然后以群为抽样单元,从总体中随机抽取一部分群,对入选群内的所有单元进行统计分析[10]。以该小区为例,以每10栋楼为1群,则99栋有效楼栋(实际安装了室温测点的楼栋)可划分成9个群,再随机抽取1个群进行整体抽样。楼栋划分方法:1#、11#、21#、…、91#为第1个群;2#、22#、32#、…、92#为第2个群;…;9#、19#、29#、…、99#为第9个群。本文以第9个群的全部室温数据作为抽样样本进行分析。

2) 系统抽样:又称等距抽样或机械抽样。即先将总体中的全部个体按与研究现象无关的特征排序编号;然后根据样本含量大小,规定抽样间隔k,随机选定第i(i

3) 分层抽样:又称类型抽样法。即将总体样本按其属性特征分成若干类型或层,然后在类型或层中随机抽取样本单位[12]。

2.2 参数估计

假设不知道小区总体室温情况,总体标准差σ未知,用样本标准差s代替,则总体均值μ的置信区间R为[13]

(1)

抽样平均误差:

(2)

在估计室温分布比例Pt时,用抽样比例p代替Pt计算估计量的标准误差,在1-α的置信度下,Pt的置信区间Rt为[14]

(3)

根据式(3)可推断整体室温区间所占比例。

不重复抽样下的抽样比例平均误差μp[15]:

(4)

不重复抽样下的抽样比例极限误差Δμp[15]:

(5)

3 室温抽样推断

3.1 抽样方法确定

对小区室温进行整群抽样、分层随机抽样、分层系统抽样,统计结果对比如表2所示。为方便抽样方式对比,分层随机抽样和分层系统抽样比例均取10%。在95%的置信度下,上述3种方法的区间比重统计结果Z值都小于临界值1.96,故认为3种抽样方法的区间比重统计结果均与总体区间比重没有显著差异。

表2 不同抽样方法的统计结果

表3给出了抽样结果与总体比重的差异,可知分层随机抽样效果最佳,以下将采用分层随机抽样法进行分析。

表3 不同抽样方法的统计分析对比

3.2 室温比例推断

为检验推断效果,采用分层随机抽样获取样本比例为10%的小区室温;然后通过比例估计推断小区总体比例区间,计算平均误差及极限误差;最后利用假设检验原理,计算Z检验下的统计结果Z值,判断抽样比例与总体比例是否具有显著性差异。

如表4所示,在95%的置信度下,Z统计结果均小于临界值1.96,故认为此时各温度区间中抽样比例与总体比例没有显著差异,推断效果较好。

表4 室温区间比例推断及误差分析(置信度95%)

3.3 不同抽样比例推断结果

采用分层随机抽样方法,对小区总体样本分别进行抽样率为5%、6%、7%、8%、9%的统计分析,结果见表5。由表5可知,在总体均值的推断中,所有抽样比例的假设检验Z统计结果均小于1.96,即认为样本均值与总体均值不存在显著差异。

表5 不同抽样比例的统计结果(置信度95%)

表6显示了不同抽样比例的统计结果分析对比。由表6可知,在抽样比例小于等于7%的情况下,在不同的温度区间内,存在假设检验的Z统计结果大于1.96的情况,即抽样比例与总体比例存在显著性差异。故认为抽样比例小于等于7%不能满足该小区抽样推断的要求;当抽样比例大于等于8%时,可满足各项统计指标的要求。

表6 不同抽样比例的统计结果分析对比(置信度95%)

4 结论

1) 与分层系统抽样和整群抽样相比,分层随机抽样更适用于本文中的室温统计。

2) 根据中心极限定理,可通过比例抽样推断方法给出室温区间比重。

3) 当室温数据的分层随机抽样比例大于等于8%时,满足各项统计指标的要求,可为确定典型室温的分布比例提供参考。