复杂地质条件下隧道施工塌方风险评估

【摘    要】：为了实现对地铁隧道施工塌方风险的有效评估，设计一种针对地铁隧道工程施工的塌方风险评估方法，提取可能对施工造成影响的风险因素，设定风险因素的等级，建立评价指标等级矩阵，计算风险指标的权重，构建地铁隧道施工塌方风险评估指标体系，引进当量法计算塌方风险并通过实例验证设计的评估方法可行。

【关键词】：复杂地质；地铁；隧道；风险评估

【中图分类号】：U455.1【文献标志码】：C【文章编号】：1008-3197（2023）01-04-03

【DOI编码】：10.3969/j.issn.1008-3197.2023.01.002

Risk Assessment of Subway Tunnel Collapse under Complex Geological Conditions

MA Zhilei

（China Railway 16th Bureau Group Corporation Limited， Beijing 100000， China）

【Abstract】：In order to evaluate effectively the collapse risk of subway tunnel construction， a collapse risk assessment method for subway tunnel construction is designed， which extracts the risk factors that may affect the construction， sets the level of risk factors， establishes the evaluation index level matrix， calculates the weight of risk indicators， and constructs the subway tunnel construction collapse risk assessment index system， The equivalent method is introduced to calculate the collapse risk， and the feasibility of the evaluation method is verified by an example.

【Key words】：complex geology； metro；tunnel； risk assessment

隧道工程一般都處于复杂地质条件下，由于施工风险过于隐蔽，具有不确定性、随机性、复杂性等特点，导致施工人员无法及时感知或识别 [1]。为了及时掌握并有效感知施工中的风险，本文将施工中的复杂地质条件作为研究背景，从风险评估指标体系构建、评价指标等级矩阵与权重计算、基于当量法的塌方风险计算与评估结果量化3方面，设计一种针对地铁隧道工程施工的塌方风险评估方法。

1 复杂地质条件下地铁隧道施工塌方风险评估

1.1 评估指标体系构建

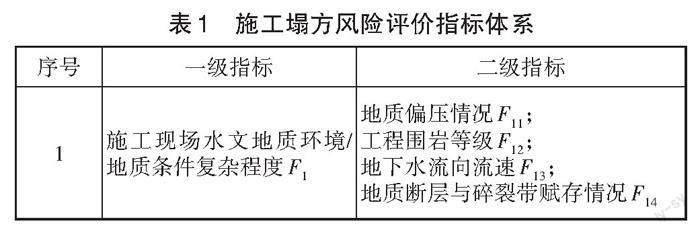
为了及时感知地铁隧道施工中的塌方风险，在开展相关研究前，需要进行塌方风险评估指标体系的构建。虽然不同工程项目施工特点不同，但各类型工程都具有施工风险的共性特征[2]；对指标进行细化与筛选，优选指标集合中影响力较大、重要性更高的指标，将评价指标控制在5～10个范围内[3]。见表1。

1.2 建立评价指标等级矩阵与权重计算

提取每个可能对施工造成影响的风险因素，设定每一个风险因素的等级均为m，不同等级的风险因素，对施工现场的坍塌事故所造成的影响是不同的[4]。将等级为m的风险因素对施工现场安全的影响程度表示为一个隶属度函数，参照标准的评价矩阵，进行影响程度的描述。

[Ri=ril1   L   rilk      Orinl   L   rink] （1）

式中：[Ri]为针对塌方风险评估指标[i]构建的评价矩阵；[ril1]为指标[i]在维度[l]下的风险；[L]为风险指数；[rilk]为指标[i]在维度[k]下的风险；[O]为无风险施工行为。

应注意的是，不是评价指标体系中所有指标都可以用评价矩阵表示。例如，指标体系中的定量化指标（隧道整体结构跨度F51、施工循环进尺方式F22等），需要使用梯形隶属度函数对其进行描述。指标体系中的地质偏压情况F11、工程围岩等级F12、地下水流向流速F13等无法定量描述，需要在建立评价矩阵时，基于定性角度对其进行模糊表示[5]。

在完成评价指标等级矩阵的建立后，建立不同指标的权重集合，计算指标权重值，进行指标重要度的分析[6]。在此过程中，可设定[a]、[b]两个参数，[a]表示指标因素、[b]表示等级，将[a]的取值定义在1～n之间，[b]的取值定义在1～m之间；则[iab]可以表示为指标[i]中第[a]个因素的第[b]个等级。

对[iab]进行归一化处理

[nmiab=1] （2）

在完成对[iab]的处理后，引进层次分析法（AHP），确定不同评价指标的权重值。为避免复杂的评价过程对评价结果造成影响，采用一级模糊计算的方式，进行单个指标中独立因素的权重计算[7]。

[Bi=abRi]  （3）

式中：[Bi]为指标[i]在风险评价过程中的权重值。

根据式（3）计算评价指标体系中不同指标的权重值，掌握并及时感知不同指标在评价中的优先级与重要程度。

1.3 基于当量法的塌方风险计算与评估结果量化

施工中塌方事故往往是由多方面因素造成的，综合当前隧道施工塌方风险评估方式并考虑经济损失、人员伤亡、工期延误等因素，確定塌方风险的严重程度，在这一过程中，引入当量法对风险进行计算。将塌方发生后不同后果按照相关规定一级标准进行量化，使其与一个当量的严重程度相互抵消，进而实现对结果的量化归一。

[DC=z300+d1+K10]  （4）

式中：[DC]为塌方风险评估结果量化值；[z]为发生塌方后造成的直接经济损失；[d]为伤亡人数；[K]为工期延误时间。

式（4）计算得出的结果可作为塌方风险发生后量化评估结果。

评估过程中，为了确保风险计算准确性，还需要确定最终塌方风险的可能性等级。见图1。

在确定塌方风险可能性等级的基础上，对塌方出现后造成的损失进行量化，确定塌方风险具体出现的可能性。具体而言，由于地铁隧道施工过程中风险事件造成的具体后果是未知的，因此采用专家评判的方式确定塌方风险发生后事件的严重性等级；将塌方风险划分为5个不同等级，其严重程度从高到低依次为十分严重、严重、中等严重、一般严重、轻微严重。5个等级对应的延误时间依次为超过24月、6～24月、2～6月、0.5～2月、少于0.5月；上述风险等级在环境和社会影响程度上也均为从高到低。

2 应用实例

为了探究上述风险评估方法的理论设计在实际应用中是否能够解决复杂地质环境中各类因素的干扰问题，以某地区正在开展的施工项目为例，对该项目出现塌方风险情况进行具体评估。

该隧道为特长、分离式结构，左线与右线的长度相差102 m，右线略长，属于典型的特长公路隧道。为了方便施工，在隧道周围设立了2个斜井：1号斜井位于隧道南侧，与隧道左线之间的距离为123 m，综合坡度12%；2号斜井同样位于隧道南侧，与隧道左线的距离为162 m，综合坡度10%。

首先确定塌方风险评估指标体系，综合该项目实际情况，选择体系当中的地质偏压情况、工程围岩等级、赋存情况、支护成果质量、爆破管材的运输方式与抽检结果共5个二级指标，对其编号为F01、F02、F03、F04、F05；对评价指标等级矩阵进行建立，分别设定5个评价指标的权重为0.1、0.3、0.2、0.2、0.2；引入当量法对塌方风险进行计算并针对评估结果量化；结合各评估指标的结果，确定1号斜井与2号斜井的塌方风险等级。见表2。

隧道施工中，应当重点针对1号斜井给出明确的防塌方决策方案。

3 结语

通过工程实例可以看出，本文提出的塌方风险评估方法应用到真实的工程项目当中，可实现对其斜井塌方风险的等级的判定，为工程安全施工提供重要依据。

参考文献：

[1]孟继慧，夏万求，彭泽豹，等. SBM施工风险分析及管控措施——以宁海抽水蓄能电站竖井工程为例[J]. 建井技术，2021，42（6）：1-6+11.

[2]孙会良，胡盛斌，肖鹏飞，等. 地铁曲线接收段盾构近距离斜穿既有车站施工风险控制——以南宁轨道交通5号线下穿既有1号线广西大学站为例[J]. 隧道建设（中英文），2021， 41（7）：1206-1217.

[3]裴元江，史彦伟，李亚非，等. 基于FAHP-云模型的PC箱梁桥转体施工风险分析与控制[J]. 公路交通科技，2021，38（8）：101-109.

[4]金起波，刘    源. 基于AHP-模糊综合评价法的城际轨道交通工程施工风险研究[J]. 湖南交通科技，2021，47（3）：141-143+192.

[5]阮    超，张延军，李胡爽，等. 基于改进熵权-未确知测度模型的城市污水深隧下穿既有铁路施工风险评价[J]. 安全与环境工程，2021，28（6）：84-90.

[6]蒙国往，丘洪彬，吴    波，等. 基于改进层次分析法、熵权法的深基坑施工风险评估[J]. 数学的实践与认识，2021，51（21）：167-176.

[7]王景春，吴雨航，王利军，等. 基于改进属性区间识别模型的跨线公路桥施工风险评估[J]. 石家庄铁道大学学报（自然科学版），2021，34（4）：1-7.

收稿日期：2022-02-25

作者简介：马志镭（1991 - ）， 男， 河南南阳人， 工程师， 从事市政工程施工管理工作。