正态分布定数和定时截尾数据可靠性评估方法
傅惠民, 郭建超, 付越帅, 李子昂
(北京航空航天大学 小样本技术研究中心, 北京 100191)
0 引言
随着产品质量和可靠性越来越高, 产品寿命越来越长,导致寿命试验所需时间长、费用高,工程上难以承受。因此, 定数和定时截尾寿命试验目前已成为工程上一类常用的寿命试验[1]。定数截尾寿命试验是试验达到事先规定的失效数时停止试验,此时试验停止时间是随机变量;定时截尾寿命试验则是试验达到事先规定的时间停止试验,此时得到的失效数为随机变量。 定数和定时截尾寿命试验数据都不是传统的完全寿命数据, 在统计分析上比较复杂。
由于指数分布具有简单的数学形式和性质, 其推导和计算都相对容易,所以人们对于产品寿命遵循指数分布情况, 已经建立了能够根据定数和定时截尾寿命试验数据进行可靠性评估的方法, 并广泛应用于工程实践中[2]。但是, 对于工程上常见的产品对数寿命遵循正态分布的情况, 还难以根据定数和定时截尾寿命试验数据进行可靠性评估。 鉴于工程上许多情况产品对数寿命标准差均为已知[3],因此本文在文献[4-5]给出的不完全寿命数据可靠性评估方法的基础上, 进一步建立了一种正态分布定数和定时截尾数据可靠性评估方法, 能够根据定数或定时截尾寿命试验数据给出产品高置信水平、 高可靠度的可靠寿命单侧置信限或可靠度单侧置信下限, 从而使工程上许多原先无法处理的定数或定时截尾寿命试验数据得以统计分析,实现小样本可靠性评估。
1 正态分布定数截尾数据可靠性评估
定数截尾试验是工程上一类常见的重要试验, 它要求试验达到事先规定的失效数时停止试验。 下面给出产品对数寿命遵循正态分布情况下的定数截尾数据可靠性评估方法。
1.1 定数截尾数据可靠寿命评估方法
设某产品对数寿命X=lgN 遵循标准差为σ0(已知)的正态分布,其概率密度函数为
可靠度函数为
式中: μ 为对数寿命均值;Φ(·)为标准正态分布函数。
现进行了一组n 个该产品的定数截尾试验, 前r 个为失效数据xi=lgNi,i=1,2,…,r,后n-r 个为未失效数据,且xi=xr=lgNr,i=r+1,r+2,…,n。则可以证明,该产品置信度为γ、可靠度为R 的对数可靠寿命xR单侧置信下限xRL,γ可由下式给出
其置信度为γ、可靠度为R 的可靠寿命NR单侧置信下限NRL,γ则为
式中:M 根据数值计算精度要求进行取值(如104,105,106等),并且应使Mγ 为整数。然后,调整式(8)中的γ 至某一值γ**,使得式(5)中γ*等于γ,此时γ**即为所求值。
对于工程上需要计算置信度为γ、 可靠度为R 的可靠寿命NR单侧置信上限NRU,γ的情况,则将上面公式中的γ 用1-γ 代替即可。
现证明如下: 首先, 根据前r 个失效数据xi,i=1,2,…,r, 可以按照完全数据处理方法求得该产品置信度为γ、可靠度为R 的对数可靠寿命xR单侧置信下限为
满足
然后, 利用其余n-r 个未失效数据xi=lgNr,i=r+1,r+2,…,n,对的置信度进行Bayes 更新。 即将前r 个失效数据求得的式(10)作为先验分布,并将后n-r 个未失效数据作为样本数据,通过Bayes 公式求得后验分布。 由于先验分布直接根据试验数据求得, 所以确保了后验分布的客观真实。 更新后的置信度γ*可以表示为
式中:g(xR)为xR的置信分布[5]。
因此,可将式(12)和式(13)变换为
而式(16)和式(17)可以通过下面两式进行数值计算:
代入式(11),可以得到
式中:
最后,调整式(23)中的置信度γ 至γ**,使得式(20)中的γ*=γ,此时即可求得该产品置信度为γ、可靠度为R 的对数可靠寿命单侧置信下限为
将上述证明过程中的置信度换成置信水平, 仍然成立。 证毕!
1.2 定数截尾数据可靠度评估方法
由置信限曲线的等同性可知, 该产品在给定时间x=lgN 处置信度为γ 的可靠度单侧置信下限RL,γ为
2 正态分布定时截尾试验可靠性评估
同样, 定时截尾试验也是工程上一类常见的重要试验,它要求试验达到事先规定的试验时间停止试验。下面给出产品对数寿命遵循正态分布情况下的定时截尾数据可靠性评估方法。
2.1 定时截尾数据可靠寿命评估方法
设某产品对数寿命X=lgN 遵循标准差为σ0(已知)的正态分布,如式(1)所示。 现进行了一组n 个该产品的定时截尾试验,前r 个为失效数据xi=lgNi,i=1,2,…,r,后n-r个为未失效数据,且xi=x0=lgN0,i=r+1,r+2,…,n,其中N0为试验截尾时间。 针对定时截尾试验情况,可将一个未失效数据xr+1=x0看作失效数据,进而将其转化为定数截尾试验情况进行处理, 得到的结果将偏于保守。 即在式(3)中用r+1 代替r,就可以根据定时截尾试验数据求得置信水平为γ、可靠度为R 的对数可靠寿命xR单侧置信下限为
其置信水平为γ、 可靠度为R 的可靠寿命NR单侧置信下限NRL,γ仍由式(4)计算。
对于工程上要计算置信水平为γ, 可靠度为R 的可靠寿命NR单侧置信上限NRU,γ的情况,只需将式(6)中的xr换成x0,式(8)中的γ 换成1-γ 即可。
特别地,当定时截尾寿命数据均为未失效数据时,该产品置信水平为γ、 可靠度为R 的对数可靠寿命单侧置信下限为
2.2 定时截尾数据可靠度评估方法
由置信限曲线的等同性可知,该产品在给定时间x=lgN处置信水平为γ 的可靠度单侧置信下限RL,γ由下式给出
3 仿真验证
本文方法除了严格的理论推导外, 还进行了大量的Monte Carlo 模拟仿真验证,其结果表明:正态分布定数截尾数据可靠性评估方法严格满足置信度要求; 而正态分布定时截尾数据可靠性评估方法则通常高于置信度,偏于安全,满足置信水平要求。下面给出仿真方法和几组仿真结果。
仿真验证方法: 设某产品的对数寿命遵循正态分布N(μ,σ02),首先通过Monte Carlo 方法从其对数寿命母体中进行随机抽样, 分别产生该产品定数或定时截尾寿命数据。 然后根据本文方法求得其置信水平为γ、可靠度为R 的对数可靠寿命单侧置信下限xRL,γ,并使之与对数可靠寿命真值xR=μ-uRσ0进行比较。重复仿真m 次,统计xRL,γ小于等于xR的频率作为仿真置信度γ′,比较仿真置信度γ′与设定的置信度γ,即可验证本文方法的正确性。
定数截尾仿真验证:在每次仿真试验中,产生一组定数截尾寿命数据,重复仿真次数m=50000 次,表1 列出了不同条件下可靠度R=0.999 的定数截尾仿真验证结果。可以看到,仿真置信度γ′均非常接近于设定的置信度γ。倘若增加重复仿真次数m, 则仿真置信度γ′将与设定的置信度γ 完全相等。 表明本文提出的正态分布定数截尾数据可靠寿命单侧置信下限评估方法满足置信度要求。
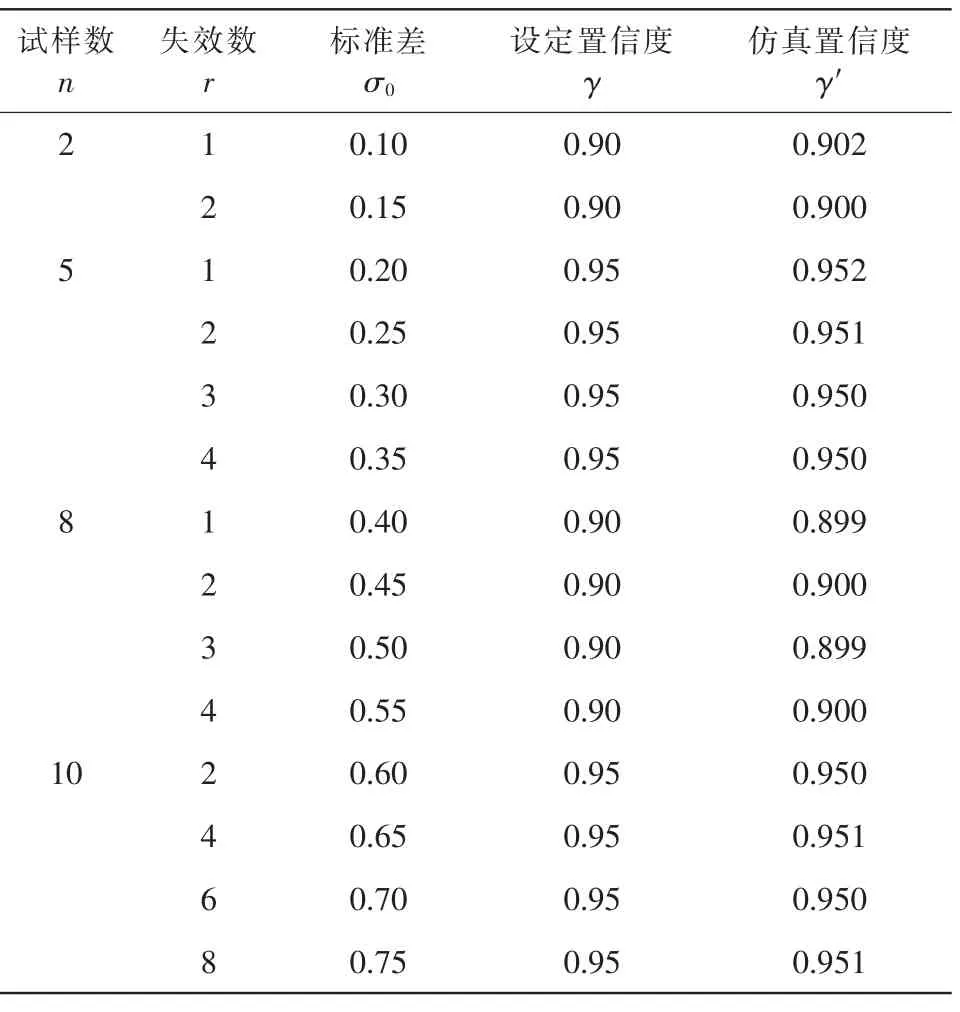
表1 定数截尾仿真验证结果
定时截尾仿真验证:在每次仿真试验中,产生一组定时截尾寿命数据,重复仿真次数m=50000 次,表2 列出了不同条件下可靠度R=0.999 的定时截尾仿真验证结果。 可以看到,仿真置信度γ′均高于设定置信度γ,表明本文提出的正态分布定时截尾数据可靠寿命单侧置信下限评估方法满足置信水平要求,略偏于保守。 此外,可以发现随着截尾时间的增加, 仿真置信度越加接近于设定置信度。倘若无限延长截尾时间,该方法将会退化为完全数据处理方法。

表2 定时截尾仿真验证结果
4 算例
已知某型航空发动机涡轮叶片对数寿命遵循标准差为σ0=0.15 的正态分布。现从一批该产品中随机抽取5 个进行振动疲劳试验, 规定循环次数达到2×107时停止试验,试验数据如表3 所示。下面采用本文方法对该产品的可靠性进行评估。

表3 某型航空发动机涡轮叶片定时截尾试验数据
首先,根据本文2.1 节方法,将一个未失效数据N2视为失效。 由式(9),利用失效数据Ni(i=1,2)计算该产品置信水平γ=0.95、 可靠度R=0.9987 的可靠寿命单侧置信下限为
最后,调整式(23)中的置信水平γ=0.95 至γ**=0.36,使得γ*=γ。 根据式(26)和式(4)可计算该产品置信水平γ=0.95,可靠度R=0.9987 的可靠寿命单侧置信下限NRL,γ为
5 结论
提出一种正态分布定数截尾数据可靠性评估方法,能够根据定数截尾寿命试验数据评估产品高置信度、高可靠度的可靠寿命单侧置信限, 以及给定时刻下高置信度的可靠度单侧置信下限, 解决了长期以来正态分布定数截尾数据难以进行可靠性评估的问题。
针对工程上常见的正态分布定时截尾寿命试验,进一步建立一种正态分布定时截尾数据可靠性评估方法,使工程上许多原先无法处理的定时截尾寿命试验数据得以统计分析,实现小样本可靠性评估。
严格的理论推导和大量的Monte Carlo 模拟仿真,证明了本文方法的正确性。

