基于动态主题模型的往复机械故障早期预警方法

张铭光 骆学理 贾 登 张 易 马 波*

(1.北京化工大学机电工程学院, 北京 100029;2.北京化工大学高端机械装备健康监控及自愈化北京市重点实验室,北京 100029;3.中国石油集团工程技术研究院有限公司, 北京 102206)

引 言

往复式压缩机、柴油机等复杂往复机械作为流程工业中的关键设备,其运行可靠性直接影响企业的安全生产,建立可靠的故障预警系统是保证设备安全运行的必要举措。 由于往复机械结构复杂,其运行信号具有非平稳性的特点,致使实现故障的早期预警较为困难[1]。

如何综合利用多特征参数实现对往复机械运行状态的有效监测,已成为设备故障预警领域研究的热点。 李一青等[2]提出基于自组织神经网络的多特征融合方法,构建准确反映轧机自激振动趋势的特征指标,通过判断特征指标是否超过阈值来实现故障预警。 马波等[3]基于主题模型技术建立相空间的主题分布,根据往复压缩机不同工况相空间主题分布的差异性,实现设备的异常检测预警及故障诊断。 吴定海等[4]提出基于双树复小波变换的振动特征提取方法,利用特征向量训练得到的后向传播神经网络对柴油机进行故障预警。 马波等[5]提出基于变分自编码器的机械故障智能预警方法,自学习机械振动信号的高维特征统计分布模型,通过分析模型的变化实现智能预警;他们还提出基于降噪自编码器的机械故障智能预警方法[6],将高维监测数据编码成低维特征,通过度量待测样本编码特征与基准的距离实现故障预警;之后他们又构建了高维特征相空间并采用无线t 混合模型对其进行拟合[7],依据模型的变化实现智能预警。 郭鹏飞等[8]将特征变量和标签数据导入随机森林算法,随后建立了一种监测变桨轴承磨损的预警模型。

基于神经网络的故障预警方法需要大量的故障样本用于训练神经网络,然而工业现场难以获取故障数据,导致该类型方法较难实际应用。 基于统计学习的故障预警方法利用设备正常数据训练模型,但目前该类型方法每次生成混合模型都需要重新估计先验参数,未建立设备不同时刻运行状态之间的有效联系,同时增加了生成混合模型耗时,对故障预警的准确性和时效性均造成影响。

主题模型是文本主题归纳中常用的方法,动态主题模型(dynamic topic model, DTM)则是在传统静态主题模型基础上引入时间维度,使得模型能够显示主题在特定时间间隔之间的变化。 赵美玲等[9]利用基于动态主题模型的舆情本体概念抽取方法,成功发掘出依时间变动的互联网舆情主题。 蒋卓人等[10]采用一种结合有监督学习的动态主题模型(该模型可准确反映文档的主题结构),精确捕捉到了主题-词汇概率分布的动态演化。 鉴于其优异的动态建模能力,DTM 在文本主题挖掘和图像分析等领域取得了非常优异的应用效果,然而在机械故障预警领域尚未有所应用。 本文首次将DTM 引入机械故障预警领域,对基于统计学习的故障预警方法进行改进,提出一种DTM 结合学生t 分布的往复机械预警模型建模方法(DtMM)。 该方法固定混合模型内子成分的顺序结构,依据DTM 建模原理建立混合模型与基准混合模型之间的参数演化关系,新的混合模型由基准混合模型结合输入数据演化而来,通过计算混合模型与基准混合模型的差异来表征设备实时工况状态与正常状态的差异,以此实现对设备的状态监测。 最后分别采用往复压缩机工程案例数据和故障试验数据对提出方法的有效性进行验证。

1 动态主题模型与变分推断

1.1 动态主题模型

DTM 在传统隐含狄利克雷分布(latent Dirichlet allocation,LDA) 方法的基础上进行了延伸,在底层主题多项式的自然参数空间上使用状态空间模型,使得主题可以在时间序列下演变。 对于样本-主题概率分布,采用均值为α的逻辑正态分布来表示概率分布的不确定性,使用简单的动态模型建立模型之间的顺序演化关系[11]。 如式(1)所示,将主题和主题概率分布相关联,得到一组主题模型。 一组有序样本在时间切片t上的生成过程表述如下。

1)生成狄利克雷分布βk,t

式中,βk,t表示时间切片t所对应主题k的数据分布,N代表高斯分布,σ2I表示高斯噪声过程。

2)描述主题随时间的变化

式中,α表示每个样本可能的主题分布,σα表示逻辑正态分布的标准差,I表示参数传递过程。

3)对每个输入样本

(a)生成样本-主题分布参数η

(b)对于样本中的每个数据点

i.生成样本-主题分布Z

ii.生成各主题下数据Wt,d,n

式中,Mult表示映射过程,π(x)将多项自然参数映射为平均参数,可表示为

式中,w表示生成数据点的数量。

1.2 变分推断

对于混合模型参数推断,传统的静态主题模型采用Gibbs 采样进行参数估计[12],但由于DTM 中高斯模型和多项式模型存在非共轭性,导致Gibbs 采样收敛性差,因此采用收敛较快的变分推断对混合模型参数进行估计。 通过不断更新变分变量,来不断减小变分分布与真实后验分布之间的距离,当距离值小于预先设置的阈值后,即可将变分分布作为真实后验分布的近似替代[13-14]。 为了求取统计变量Φ={Z,μ,Λ,u,V,α}的真实后验分布p(Φ|X),引入一个变分分布q(Φ),其分解形式表示为

数据样本X与全部统计变量Φ= {Z,μ,Λ,u,V,α}的联合分布表示为

为了实现推断目标,引入一个对数边缘似然的等式,如式(9)所示。

式中,F表示lnp(X)的变分下界;KL(q‖p)为q(Φ)与p(Φ|X)之间的Kullback-Leibler 散度。 由于KL(q‖p)越小,q(Φ)与p(Φ|X)越相近,根据式(9),可通过最大化变分下界F来达到优化q(Φ)的目的。

2 往复机械故障早期预警方法

2.1 方法流程

往复机械作为一种复杂机械,其振动响应信号往往由多个激励源信号叠加而成,因此呈现出较强的非平稳性。 若设备发生故障,往往会引起单个或多个激励源信号分布发生变化,最终引起振动响应信号分布发生变化[15-16],其振动响应信号如式(10)所示。

式中,ri表示振源到传感器的传递距离;Vk表示w(ri,t)间相互独立的冲击强度;w(ri,t)表示t时刻的振动冲击波形;N(ri,t)即泊松过程,表示脉冲冲击计数变量。 当考虑时变传递路径h(ri,t)的影响时,非平稳振动响应信号如式(11)所示。

式中,f(ri,τ)表示激励源响应函数,i=1,2,…,m,j=1,2,…,n;N(r,t)表示高斯噪声。

在设备故障早期,损伤部件与其他部件相互作用会使响应信号的分布产生变化。 DtMM 方法可自学习其统计分布,在基准模型基础上不断演化生成新的混合模型,通过计算设备实时运行工况下混合模型和基准混合模型的差异来判断设备状态是否出现异常,以此实现设备运行状态的监测。 响应信号的分布的变化可能由单个或多个部件故障引起[17],该变化可由某些特征反映,若设备运行状态发生改变,其特征值必然发生变化。 因此,选取往复机械监测参数的敏感特征构造特征矩阵,将特征矩阵作为DtMM 方法模型训练和测试的输入,可准确识别设备状态的异常变化。

所提方法的预警流程如图1 所示,主要分为特征矩阵构建、基准混合模型和实时混合模型训练、报警阈值自学习与故障预警应用3 个部分。

图1 DtMM 故障预警流程图Fig.1 Fault early warning process of DtMM

2.2 DtMM 模型

DtMM 模型由多个t-分布线性叠加而成,t-分布具有一个控制拖尾长度的自由参数v,可以很好地拟合往复机械拖尾性振动信号u(ri,t),具备较强的鲁棒性[7]。 混合模型概率密度函数表示为

式中,Θ= {πj,μj,Λj,vj}表示混合模型参数集,其中j为子模型序号,μ为均值矩阵,Λ为协方差矩阵,v为自由度;π=(π1,π2,…,πk)T为子模型权重向量;K为子模型的数量。 DtMM 概率图模型如图2 所示。

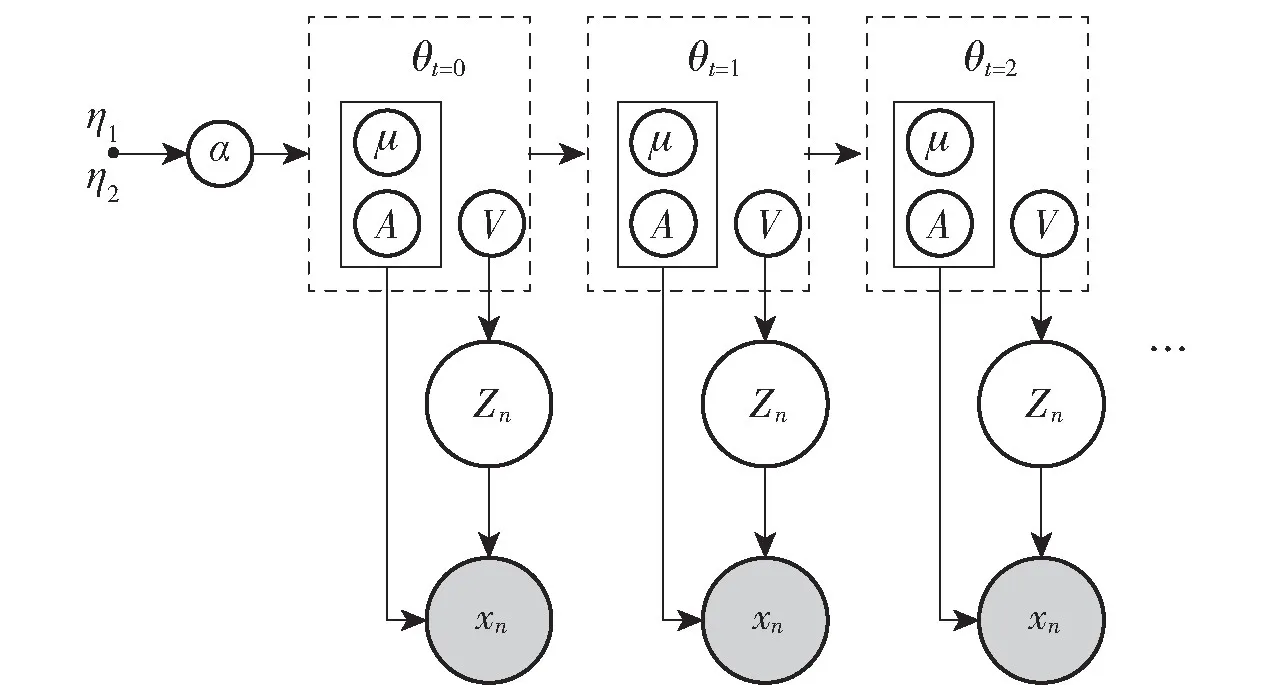
图2 DtMM 模型生成示意图Fig.2 DtMM model generation schematic diagram

对于数据集Di,t=(d1,n,d2,n,…,dm,n)T,di,n是由n个特征构成的特征向量的表示,DtMM 基于Di,t生成混合模型的步骤分为两部分。

1)在初始时刻(t=0),初始化混合模型参数集Θ,依据振动数据自学习响应信号中激励源的数量以及各激励源信号的统计分布。 混合模型中子模型参数的先验服从狄利克雷过程,在xn的生成过程中,引入一个隐统计变量zn,用于确定xn所属的子模型, 生成过程如下。

式中,π(V) ={πj(V)},zn服从多项分布。2)设备故障的发生往往伴随着缓慢的劣化过程,当前时间片的激励源分布与前一时间片的激励源分布存在着紧密的联系。 为了准确描述这种关系,在新的混合模型生成过程中,将激励源信号所服从的统计分布作为节点映射时序混合模型,通过逻辑正态分布链接前一时间片混合模型的样本-激励源分布,根据当前时间新增的数据样本更新激励源-数据分布,生成过程如下。

式中,N(Θt-1,σ2I)为正态分布。

2.3 构造特征矩阵

获取往复压缩机K组正常工况振动数据作为训练集,M组不同类型故障的振动数据作为测试集,经特征提取后构建特征向量矩阵,记为Di,t。

式中,Di,t表示第i个样本,t表示该样本对应时刻,di,j表示第i组数据中第j个特征的特征值,i∈1,2,…,m,j∈1,2,…,n,m表示数据集的长度,n表示故障特征的数量。

2.4 训练模型

训练样本Di,t0用于训练基准混合模型,训练样本Di,ti,i∈[1,k]用于训练正常状态混合模型。 具体实施步骤如下。

1)输入特征矩阵Di,t0,初始化基准混合模型,利用狄利克雷过程生成混合模型先验参数,即基准混合模型中的子模型数量及权重参数。

2)基于步骤1)计算结果,结合变分推断计算基准混合模型后验参数,即子模型分布参数,得到基准混合模型mstandard并将其保存。

3) DtMM 基于mstandard分布参数演化生成正常工况混合模型先验参数,结合训练样本D1,t1,采用变分推断计算混合模型后验参数,得到第一个正常状态混合模型m1,并计算m1与mstandard的模型差异值。

4)依次输入训练样本Di,t,i∈2,…,k,重复步骤3),得到正常状态混合模型与基准混合模型差异集,用于自学习报警阈值。

2.5 自学习预警阈值

统计模型距离评价方法包括KL 散度、余弦距离、JS 距离和杰卡德相似系数等,其中KL 散度通过计算两个模型的相对应成分间的差异来综合表征两个模型间的距离[18]。 DtMM 生成的模型由多个t-分布组成,KL 散度逼近方法通过计算t-分布的差异来表征不同模型之间的距离,故结果更加精确,因此本文采用KL 散度逼近方法计算混合模型mi与基准混合模型mstandard的距离,计算过程如式(23)所示。

其中,

式中,KL(mi(j)‖mstandard(j))表示混合模型中第j个子模型与基准混合模型中第j个子模型的KL 散度,即两个t-分布的KL 散度。

预警阈值依据设备正常状态数据自学习获得,具有较强的自适应性和高的可靠性。 训练k个正常状态混合模型mi,统计mi与mstandard的距离,并计算其均值μkd和方差σkl。 设备处于正常运行状态时,正常状态混合模型mi与基准混合模型mstandard差异较小,可认为两者距离近似服从正态分布。 因此,将报警阈值T设定为μkd±3σkl。 获得报警阈值T后,当实时工况混合模型monline与基准混合模型间mstandard的KL 散度超过T时,认为设备发生故障,触发报警。

3 试验验证与结果分析

为全面、准确地评估提出方法的有效性,分别利用往复压缩机故障模拟试验数据(数据集A)和工程案例数据(数据集B)对方法进行验证。 为验证提出方法的准确性,结合数据分析和测试结果,统计报警结果中存在的误报、 漏报次数并计算预警准确率。 误报、漏报均认定为错误报警,预警准确率以单个测试集为最小计算单位,每个测试集包含244 个测试样本。 预警准确率A计算公式表示为

式中,DL表示单测试集包含的样本容量,本文中DL均为244,FP表示误报次数,UP表示漏报次数。 分别统计数据集A 和数据集B 中测试集的预警准确率,计算其平均预警准确率,以此对提出方法的准确性进行定量评估。 为验证提出方法的时效性,从提前预警时间和生成混合模型耗时两方面进行评估,预警时刻与故障时刻时间差越大,生成混合模型耗时越短,表明预警方法的预警时效性越好。 为验证提出方法的可靠性,从预警指标变化趋势方面进行评估,通过预警指标的平均标准差来表征其平稳性。为反映提出方法的先进性,将变分自编码器(variational auto-encoder,VAE)方法[5]、无限学生t 混合模型(infinite student's t-mixture model,iSMM)方法[7]和基于数据驱动随机森林(random forest,RF)的风电机组变桨轴承磨损预警建模方法[8]作为对照试验进行方法对比。

3.1 数据描述

(1)数据集A

数据集A 来自往复压缩机试验台,包含8 种故障类型数据,即吸气阀阀片断裂、吸气阀弹簧失效、排气阀阀片断裂、排气阀弹簧失效、十字头销磨损、活塞环断裂、活塞销松动和基座松动,共计21 个测试集;设备正常状态数据作为训练集,数量为2,具体介绍如表1 所示。 为避免设备连续状态数据对方法验证造成误差,训练集与测试集的正常状态数据分别来源于故障模拟试验前后。 往复压缩机试验台的监测传感器测点布置如图3 所示,分别在缸头、十字头上方安装加速度传感器,曲轴箱壳体两侧安装速度传感器,传感器采样频率为10 240 Hz,采样点数为6 144,往复压缩机转速为500 r/min,采样长度为往复压缩机两个运转周期。

表1 数据集A 情况Table 1 Information for data set A

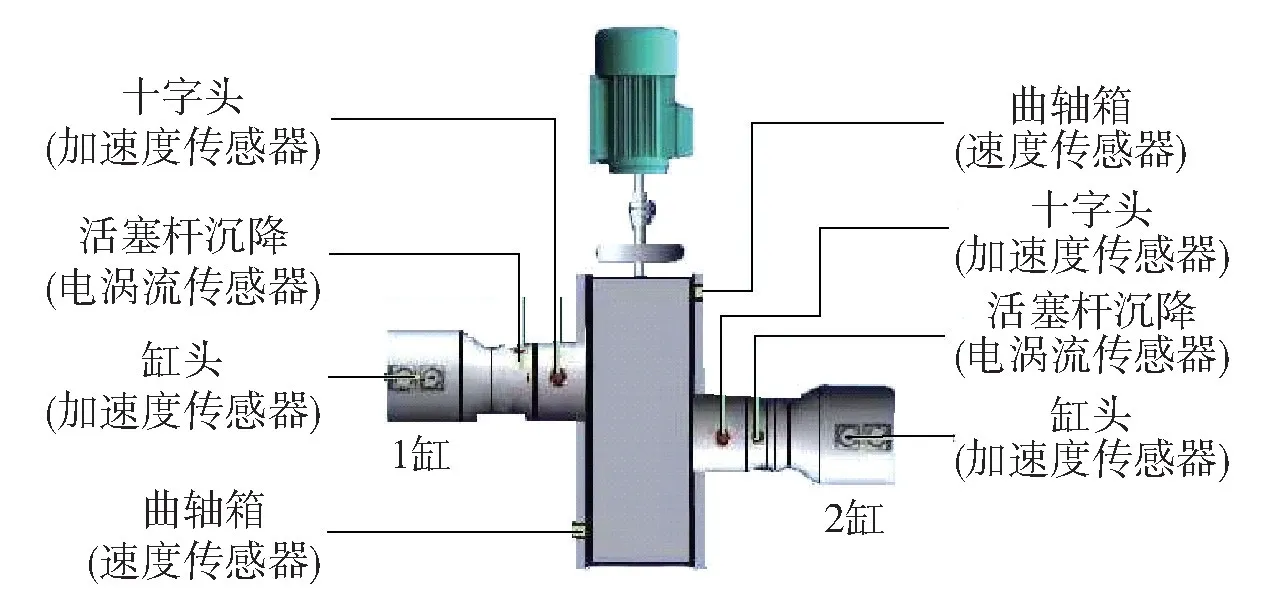
图3 测点布局及传感器类型Fig.3 Layout of the measuring point and sensor types

(2)数据集B

数据集B 来自某石化企业生产现场的往复压缩机,故障案例数据包括活塞组件磨损、气阀泄露和液击3 种类型故障,每种机组类型分别选取1 组正常状态数据作为训练集,具体介绍如表2 所示。 数据采样频率为10 kHz,采样点数为5 000,不同型号往复压缩机转速不同,转速在300 ～350 r/min 范围内,采样间隔为往复压缩机的两个运转周期。

相关测试表明,样本容量的大小对于预警方法的报警准确率具有重要影响[7]。 随着样本容量的增大,预警方法的准确率随之升高,但模型训练耗时也随之增加;当样本容量超过100 时,预警方法的报警准确率受样本容量影响较小。 因此,综合考虑预警准确率和模型的训练效率,样本容量设定为100。

3.2 特征描述

为全面、准确地反映往复压缩机的运行状态,通过分析往复压缩机旋转和往复两种运动的形式特点,依据往复压缩机不同类型故障所关联的振动信号敏感特征,分别从时频域和角度域选取了20 种特征构成模型训练和测试的特征集,如表3 所示。

表3 特征集说明Table 3 Details of the feature set

3.3 结果与分析

分别采用试验数据和工程案例数据对提出方法和对比方法进行测试,测试结果如表4 所示。

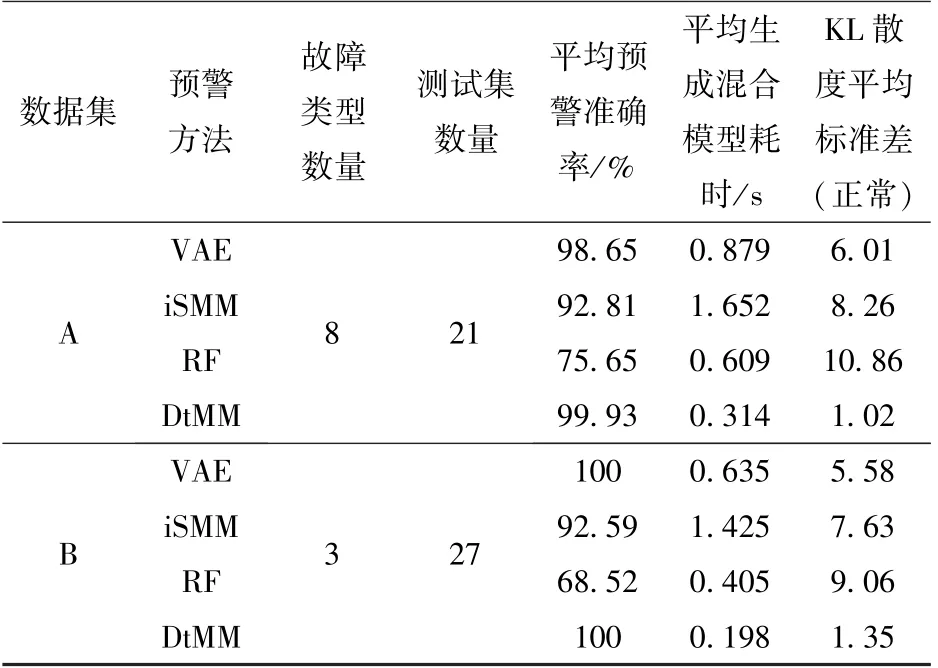
表4 方法测试结果统计Table 4 Method test result statistics

(1)数据集A 验证结果

由表4 可见,对于试验模拟的8 种故障,所提方法的平均预警准确率达到99%以上,相较于VAE方法高出1.28%,相较于iSMM 方法高出7.12%,相较于RF 方法高出24.28%,说明提出方法的预警准确率显著优于3 种对比方法。 在生成混合模型耗时方面,提出方法的平均生成混合模型耗时最短,仅为0.314 s, iSMM 方法耗时为提出方法的5 倍左右,VAE 方法耗时为提出方法的3 倍左右,RF 方法耗时为提出方法的2 倍左右,说明所提方法的时效性显著提高。 当设备处于正常状态时,提出方法的KL 散度即模型差异的平均标准差为1.02,较3 种对比方法显著降低。

(2)数据集B 验证结果

由表4 可见,对于27 组案例数据所包含的3 种故障,提出方法对27 组不同故障案例的平均识别准确率为100%,与VAE 方法相当,相比之下,RF 方法的预警准确率最低。 提出方法平均生成混合模型耗时仅为0.198 s,iSMM 方法耗时约为提出方法的7倍,VAE 方法耗时约为提出方法的3 倍,RF 方法约为提出方法的2 倍。 当设备处于正常状态时,提出方法的KL 散度的平均标准差为1.35,较VAE 方法下降75%,较iSMM 方法下降83.3%,较RF 方法下降88.9%。 数据集B 中27 组案例数据来自不同的往复压缩机机组设备,包含多种机组结构形式,提出方法均能有效实现预警,说明提出方法对于往复压缩机具有良好的适应能力。

验证结果表明:对于多种往复压缩机故障,提出方法的预警准确率优于VAE 方法、iSMM 方法和RF方法,生成混合模型的耗时显著减少,预警时效性显著提高。 在设备处于正常状态时,提出方法的KL散度平均标准差最小,预警指标随时间变化趋势的平稳性最强,说明该方法对正常运行状态产生的非平稳信号具备较强的鲁棒性。 分析发现,iSMM 方法未能对4 缸-M 型机组活塞组件磨损故障的2 组故障样本实现报警,这是由于当活塞组件磨损程度较轻时,因故障产生的数据离群点数量较少,致使iSMM 方法无法识别设备活塞组件磨损故障。 VAE方法和iSMM 方法生成的混合模型之间无有效关联信息,在每次生成混合模型时都需要对混合模型先验参数进行重新计算,该过程不仅导致生成混合模型耗时增加,同时在计算模型差异时,需要匹配混合模型之间子模型的对应关系,该过程存在不可避免的计算误差,造成预警指标变化趋势的平稳性较差。RF 方法采用随机森林算法,擅长处理高维数据和特征遗失数据,对于低维数据(特征较少的数据)的分类表现较差。 因此,对于往复机械活塞环磨损、拉缸等故障特征较少的机械故障,RF 方法的识别准确率较低。

以工程案例中2 缸D 型机组气阀泄漏故障为例,通过将预警指标可视化,以图像的形式直观地将提出方法和3 种对比方法的验证结果进行展示说明。 设备正常状态和气阀泄漏故障振动响应信号波形图如图4 所示,由图4(a)可看出,往复压缩机处于正常状态时,特定相位的冲击信号符合往复压缩机在运转过程中气阀落座、弹簧释放等部件的动作状态。 由图4(b)可看出,发生气阀泄漏故障时,气阀开闭相位附近出现多种频率信号成分,信号幅值整体减小,表明气阀泄漏故障造成振动激励。

图4 气阀不同状态的角域振动信号对比Fig.4 Comparison of valve vibration signals in different states

提出方法和3 种对比方法对于气阀泄漏故障的测试结果如图5 所示。 在气阀泄漏故障案例测试集中,气阀泄漏故障发生时刻为第148 h。 如图5(a)所示,VAE 方法在第58 h 开始报警,相较故障发生时刻提前90 h;从预警指标(KL 散度)变化趋势看,当设备处于正常运行状态时,VAE 方法报警指标趋于平稳,但波动较为明显,存在穿越报警线现象;在报警起始时刻至故障发生阶段,报警指标呈缓慢上升趋势,但仍在报警线上下波动,部分时刻预警指标低于报警线。 如图5(b)所示,iSMM 方法在第67 h开始报警,相较故障发生时刻提前81 h;当设备处于正常运行状态时,iSMM 方法报警指标波动范围较大,可明显观测到穿越报警线现象。 如图5(c)所示,RF 方法在第57 h 时开始报警,相较故障发生时刻提前91 h,从图中可看到在报警时刻后,预警指标表现十分不稳定,且在故障发生时刻之后预警指标回落到报警线下,存在较为明显的漏报问题。 如图5(d)所示,DtMM 方法在第43 h 开始报警,相较故障发生时刻提前105 h,预警时间比iSMM 方法提前24 h,比VAE 方法提前15 h,比RF 方法提前14 h;设备处于正常运行状态时,DtMM 方法报警指标变化趋于平稳,且未发现较明显波动;在设备故障早期阶段和故障发生阶段报警指标均高于报警线。 通过以上对比可以看出,提出方法可准确识别往复压缩机此类复杂机械的异常状态,设备故障早期阶段预警时间明显增加,同时预警指标变化趋势的平稳性显著优于上述3 种方法。

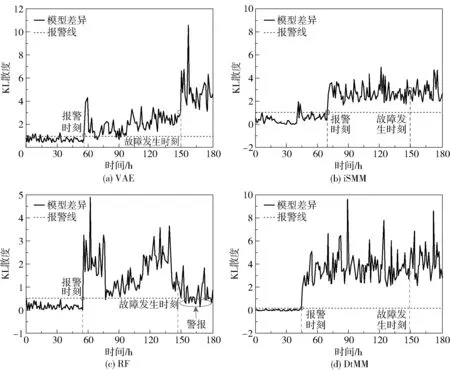
图5 4 种方法KL 散度测试结果Fig.5 KL dispersion test results of the four methods

验证结果表明:在往复压缩机运行状态监测过程中,当设备处于正常运行阶段时,提出方法能够有效克服非平稳信号对预警指标造成的干扰,预警指标变化趋势的平稳性显著增强,有效降低了误报率;在设备故障早期阶段,提出方法预警时间明显增加,能够在故障早期阶段准确识别往复压缩机的故障信号,预警时效性显著提高。 提出方法的预警准确率和时效性明显优于3 种对比方法。 VAE 方法深入振动响应信号组成成分,对激励源信号进行分析,但未考虑前一时间段的激励源信号分布对后续信号变化的影响,每次生成混合模型都需要对混合模型先验参数重新估计,生成的混合模型之间无关联信息,因此计算实时工况混合模型与基准混合模型的差异时,需事先匹配子模型的对应关系,这一过程不仅增加了计算耗时,同时造成模型鲁棒性较差,在设备正常状态下易发生误报。 iSMM 方法准确拟合了机械振动响应信号中的激励源信号统计分布,但其生成混合模型机制同VAE 方法一致,造成在设备正常状态时,报警指标易受非平稳信号影响而产生大幅波动,导致预警模型可靠性较差。 RF 方法对低维数据的分类效果较差,对于往复机械部分敏感关联特征较少的故障,该方法无法有效识别,导致预警模型的往复压缩机监测能力均存在一定的局限性。

4 结论

(1)本文提出一种基于动态主题模型的往复机械故障早期预警方法。 该方法在基准混合模型基础上生成新的混合模型,而非完全基于数据,利用状态空间转移链接混合模型间的参数,利用输入数据更新模型部分参数。 这一过程确立了混合模型中的子成分位置,依据输入数据确定子成分分布,在计算混合模型与基准混合模型差异时省去了子成分匹配计算过程。 因此,提出方法预警模型的鲁棒性更强,对于非平稳性信号的适应性更好。

(2)分别利用往复压缩机工程案例数据和试验台故障数据对提出方法的有效性进行了验证。 结果表明,对于往复压缩机故障早期预警,所提方法生成混合模型耗时减少、预警时间提前、预警误报率低,取得了很好的效果。