改进DQN算法在WSNs资源分配中的应用

郑 岚,徐丽萍

(安徽三联学院 电子电气工程学院,合肥 230601)

无线传感器网络(Wireless Sensor Networks, WSNs)资源有限,当节点资源消耗殆尽,WSNs就会失效或死亡,从而引发服务中断、假警报等各种不良后果,因此提高WSNs资源利用率是目前最有效的网络能耗解决方法之一[1]。通过合理分配,能够让各种资源之间相互配合,降低能源损耗,从而达到提高WSNs资源利用率目的[2]。

在上述的背景下,关于网络资源分配的研究有很多,不同的专家和学者提出了不同解决方法。张玉琴等[3]将最大-最小保密率作为目标函数,然后利用改进启发式优化算法对目标函数进行寻优求解,得到的最优解就是网络资源分配方案。王海峰等[4]以WSNs中的节点资源为对象,在考虑节点间距的基础上,以吞吐量为优化目标,在数据传送路径、节点通信容量、节点布局3个约束条件下,通过贪婪算法进行求解,得到WSNs节点资源的分配方案。虽然前人研究取得了一定的研究成果,但是存在2个缺陷:1)多数都是针对单一资源分配设置目标函数;2)最后的求取算法本身存在一定的缺陷。在双重问题作用下,得到的分配方案失衡,综合效益不高。本文将改进的深度Q网络(Deep Q-Network,DQN)算法应用在WSNs资源分配中,通过进一步完善网络拓扑结构,设计网络资源优化模型,提升网络资源的均衡负载水平,研究分为WSNs拓扑结构、多目标函数及分配方案求取3个部分。通过本研究以期提高WSNs资源的利用率,延长WSNs使用寿命。

1 设计与分配方案

1.1 网络拓扑结构设计

WSNs具有体积小、成本低、易于部署等优点,因此在很多领域都发挥重要作用。例如,在环境监测领域可以通过在监测区域内布设传感器,实时感知该区域内的环境信息,采集空气质量、温度、湿度、风速等信息;WSNs还可以被应用到医疗卫生领域,通过让患者佩戴传感器,实时感知患者的体征信息,如脉搏、呼吸以及体温等[5]。此外,WSNs还可以应用到军事领域、建筑领域、交通领域。WSNs结构设计如图1所示。

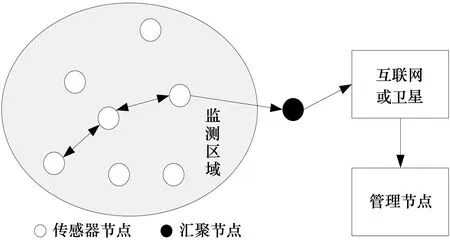
图1 WSNs结构

传感器节点包括数据采集单元、数据传输单元、数据处理单元和能量支持单元[6]。节点位置可以随时改变,通过无线通信形成的多跳自组织网络可以无线连接到物联网[7]。为方便描述,将WSNs拓扑结构通过有向无环图表示,即A={B,C,D},其中:B={b1,b2,…,bn}为无线传感器节点;C={c1,c2,…,cm}为无线传感器节点之间的链路;D={d1,d2,…,dk}为WSNs中节点之间链路的初始资源信息。

假设WSNs具有以下属性:

1)WSNs拓扑结构已知;

2)WSNs节点数量和位置已知;

3)在WSNs中不考虑节点冲突问题;

4)WSNs节点都具有相同的感应数据生成速率;

5)WSNs初始资源信息已知。

1.2 多目标优化模型构建

本文选择多个目标构建优化模型,与单一目标优化模型相比,多目标模型下求取的WSNs资源分配方案更具有全局性,综合效益更高。WSNs资源分配的理想状态是误码率最小化、网络链路容量最大化、资源分配负载均衡度最大化、网络节点能耗最小化[8]。从上述可知,优化目标不一致,为保证多目标优化中目标函数的一致性,均将最大化问题转化为最小化问题,即取最大化的负值[9]。另外,由于每个目标的重要程度不一样,因此需要对每个目标进行赋权,最终构建的多目标优化函数如下:

Ymin=w1y1min+w2(-y2max)+w3(-y3max)+w4y4min。

(1)

式中:Ymin为多目标优化最小值;y1为误码率;y2为网络链路容量;y3为资源分配负载均衡度;y4为网络节点能耗;w1、w2、w3、w4为4个优化目标的权重,w1+w2+w3+w4=1。

1)误码率。

(2)

式中:aij为数据在链路cij上传输时,链路接收端j的信噪比;E为噪声带宽;eij为数据传输速率。

2)网络链路容量。

(3)

式中:G为可用信道的带宽;gij为信道频谱宽度;dij为链路cij的频谱宽度;Dij为链路cij的通信距离。

3)资源分配负载均衡度。

(4)

式中:P为时隙集合;Q为信道集合;Jpq为第p个时隙第q个信道的链路容量之和;o为时隙的个数;u为信道的个数。

4)最大化网络生命期。

(5)

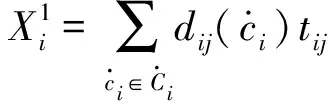
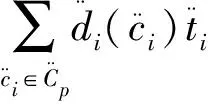
针对式(1)设置以下约束条件:

(6)

式中:Gmin、Gmax分别为信道带宽下限和上限;D总为链通信总距离;emin、emax分别为数据传输速率下限和上限;d总为链路频谱总资源量。

式(1)与式(6)共同构成多目标优化模型。

1.3 改进DQN算法求解分配方案

在完成多目标优化模型构建后,需要求取最优分配方案[10],即解出最优解。求取最优解的最佳方法就是通过寻优算法不断迭代,优胜劣汰,一步一步排除非优解,最终剩下的1个解就是最优解[11]。在这里选取的寻优方法为DQN算法。DQN算法是深度强化学习中的一种,该算法中主要有2个网络:1)当前值网络;2)目标网络。其中前者通过从经验池中获取训练样本,进行训练,目的是调整网络参数并将该参数全部赋值给目标网络;后者是利用训练好的目标网络,通过输入测试样本,得出最优结果。然而,该算法在实际应用中很容易出现过估计问题,也就是某个状态下次优动作的值将超过最优动作的值。该问题的出现不仅会影响算法整体稳定性,更为重要的是很可能导致最优解永远找不到[12]。此外,在上述基础DQN算法中,经验池的参数更新采用随机经验回放机制来实现。这种方法不仅效率低,而且奖励很小。面对上述2种问题,本节从2个方面对DQN算法进行更新。

针对过估计问题,在DQN算法的基础上进行改进,改进后DQN算法为:

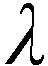
(7)

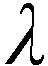
针对基础DQN算法的随机经验回放机制进行改进,设计一种自适应多采样经验回放机制,具体过程如下:

步骤1:经验样本输入。

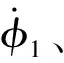
步骤4:根据权值概率随机选取采样模式。

步骤5:判断更新模式是否为随机采样?若是,执行简单随机采样原则;若否,进入下一步。

步骤6:判断更新模式是否为就近采样?若是,执行就近采样原则;若否,进入下一步。

步骤7:执行优先经验回放。

基于改进后的DQN算法,具体求解过程如图2所示。

上述过程求取的最优解就是WSNs资源分配方案。

2 实验测试

2.1 WSNs拓扑结构

为测试改进DQN算法在WSNs资源分配中的应用效果,在Matlab环境下构建1个500 m×500 m的研究区域。随机在研究区域内部署30个无线传感器节点,如图3所示。

图3 初始化传感器节点的分布

仿真参数设置如表1所示。

2.2 改进DQN算法参数设置

改进DQN算法求解WSNs资源分配方案时,所设置的初始化参数如表2所示。

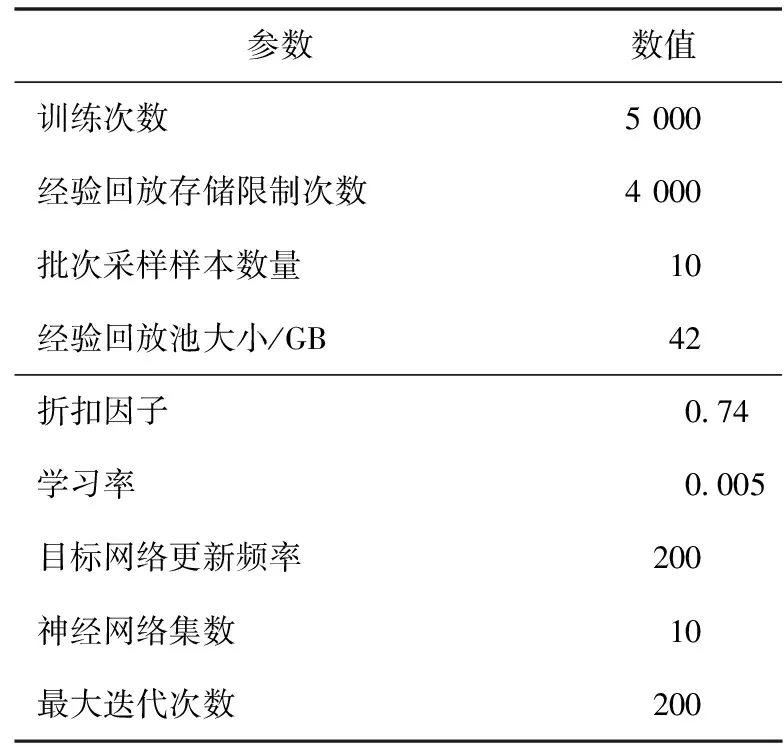
表2 改进DQN算法参数

2.3 应用效果对比分析

设置任务量100～1 000,分别使用改进DQN算法、改进启发式优化算法(算法1)、贪婪算法(算法2)进行求解,得出WSNs资源分配方案,然后运行WSNs资源分配方案,统计每个方案的传输延迟以及节点总能耗。传输延迟越小,节点能耗越少,证明WSNs资源分配方案越合理,即所研究算法的应用效果越好。结果如图4和表3所示。

从图4和表3中可以看出,与算法1、算法2得出的WSNs资源分配方案相比,随着任务量的增多,本文算法求取的WSNs资源分配方案的传输延迟更低、节点总能耗更小,方案综合效益更好,由此证明了本文算法在WSNs资源分配中的应用效果。

图4 传输延迟对比

3 结束语

本文针对WSNs资源有效分配,提出一种改进DQN算法,以提高网络资源利用率,将算法模型误码率最小化,随之将网络链路容量最大化和资源分配负载均衡度最大化综合了多个单一目标函数并利用改进DQN算法进行求解,得出了WSNs资源分配方案。最后通过WSNs资源分配方案应用下的传输延迟和节点总能耗对改进DQN算法应用效果进行对比,证明了其有效性。本文基于网络资源分配的视角提升了WSNs的均衡度,在未来应进一步完善网络拓扑结构,优化网络链路的性能。