面向通信信号调制识别的半监督生成对抗网络框架

周华吉,徐 杰,郑仕链,沈伟国,王 巍,楼财义

(1. 电磁空间安全全国重点实验室, 浙江 嘉兴 314033; 2. 西安电子科技大学 人工智能学院, 陕西 西安 710071)

通俗来说,通信信号调制识别,就是挖掘通信信号特征,以最大可能区分信号的调制类型。其在认知无线电[1-4]、频谱监测[5-6]、网络安全[7-8]等领域都有广泛的应用。通信信号调制识别主要采用模式识别方法。支持向量机对于调制识别有较好的效果,但是,核函数的选择直接影响着最终的识别结果,且算法不具有自适应能力[9]。人工神经网络自适应能力较强,但是在信噪比较低的条件下,调制识别效果不好,同时因为需要对信号的特征进行训练,计算复杂度较高[10]。近年来,深度学习技术迅猛发展,卷积神经网络(convolutional neural network, CNN)是将人工神经网络和深度学习技术相结合而产生的深度神经网络,因其强大的特征提取能力,且具备稀疏连接、权重共享等特性,有较好的调制识别效果[11-15]。然而,利用卷积神经网络进行调制识别的一个特点是需要大量带标签数据进行全监督学习。而在实际作战场景下,很多重要信号转瞬即逝,要大量获取十分困难;再则,由于电磁环境日益复杂,各种信号互相干扰,要给信号数据打上正确的标签更是难上加难,这就意味着当前几乎最优的卷积神经网络面对只有少量标签数据的弱监督条件下的调制信号识别问题,显得有些束手无策。而如何解决弱监督条件下的调制信号识别问题,也成为当前研究的一个热点和难点。

生成对抗网络[16-17](generative adversarial network,GAN)自2014年由Goodfellow提出以来,向人们展示了从无到有的神奇能力,并且已经在工业界有着广泛的应用。生成对抗网络是一种基于博弈论的学习模型,它包含两个主要成分:生成器和判别器,生成器通过接收噪声产生尽可能真实的伪数据,判别器则去分辨输入的是真实数据还是生成器产生的伪数据。双方在训练中相互博弈,训练的终点是达到纳什均衡,产生以假乱真的信号样本。虽然生成对抗网络具有强大的特征映射及逼真样本生成能力,而且在图像领域,如图像生成、分类、风格迁移等方面已经有了极广泛的应用,但由于电磁信号和图像之间存在天然的差异,因此其在调制信号识别领域的应用还极少。Tu等[18]设计了一种半监督生成对抗网络,并将调制信号以星座图的形式输入到网络中,获得了较好的调制识别效果。但是他们并没有真正实现调制信号的端到端识别,本质上还是对图像进行处理;同时半监督生成对抗网络中使用的是原始GAN, 网络训练稳定性较差。

在本文中,首先提出了一种将调制信号数据进行冗余空域变换的方法,之后利用冗余空域变换之后的数据训练出一个基于梯度惩罚Wasserstein生成对抗网络[19](Wasserstein generative adversarial network-gradient penalty,WGAN-GP)的无监督训练模型,利用其稳定的训练能力对生成器和判别器进行预训练。在获得预训练参数的基础上,设计并训练出一种二维信号半监督生成对抗网络(semi-supervised generative adversarial network for 2-dimensional signal, SSGAN-2D)模型,能将少量有标签数据和大量无标签数据都很好地利用起来。

1 信号冗余空域变换

生成对抗网络近年来取得了多方向的突破,例如从损失函数上改进使其训练更加平稳可控,从训练方式上改进使其可以从低分辨率的图像平滑过渡到高分辨率图像,从功能上拓展使其可以进行图像分类任务。这些改进方法大多集中于图像处理领域,电磁信号作为一种区别于图像的数据,如果直接套用上述的方法、模型或框架,很难取得一个令人满意的结果。因此,为了使电磁信号数据可以更有效地对应生成对抗模型,同时保持丰富的信号相邻特征,提出了一种信号冗余空域变换的方法。

假设一段电磁信号序列为A(n)={x1,x2,x3,…,xn},本文对信号序列做出如图1所示的空域变换。即,将长度为n的一维电磁信号转换成k·k的二维信号,其中k=⎣n/2」。

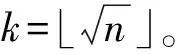
图2 传统信号空域变换Fig.2 Traditional signal spatial transformation

可以清晰地看出,当对冗余空域变换之后的信号进行卷积操作时,能充分提取信号相邻特征。而如果对通信信号序列直接进行粗暴地二维转换,则会损失很多相邻特征。

2 基于WGAN-GP的半监督分类模型

本文中,设计了一个基于WGAN-GP的无监督预训练模型,利用其稳定的训练能力对生成器和判别器参数进行预训练。之后在WGAN-GP的基础上,构建了一个SSGAN-2D模型,不仅保留了WGAN-GP利用无类别标签数据学习提取特征的能力,又使其获得信号分类能力。

2.1 WGAN-GP 结构

WGAN-GP是一个无监督模型,和原始GAN相比,WGAN-GP主要在损失函数上进行了改进,使得训练更加稳定有效。原始GAN中生成器和判别器的对抗关系为:

Ez～pz(z)(lg{1-D[G(z)]})

(1)

式中,pdata是真实数据分布,pz是噪声数据分布。D(x)表示判别器D判断真实数据是否真实的概率,而D[G(z)]则是D判断生成器G生成的数据是否真实的概率。

因此判别器的损失函数为:

JD=-Ex～pdata(x)[lgD(x)]-

Ez～pz(z)(lg{1-D[G(z)]})

(2)

实际应用中生成器的损失函数常为:

JG=-Ez～pz(z)(lg{1-D[G(z)]})

(3)

标准生成式对抗网络定义的损失函数会导致如下两个主要问题:①训练GAN需要达到纳什均衡,有时候可以用梯度下降法做到,但有时候做不到。所以训练GAN相比变分自编码器(variational auto-encoder,VAE)或者像素递归神经网络(pixel recurrent neural networks, PixelRNN)是不稳定的[20]; ②生成器和判别器的loss无法指示训练进程,而且生成式对抗网络存在模式崩溃(model collapse)的问题,具体表现为训练阶段的梯度消失使得生成的样本非常差,即使长时间训练也无法得到很好的改善。

针对上述问题,Wasserstein生成对抗网络[20]首先提出原始GAN用来衡量两个分布距离和差异的延森-香农(Jensen-Shannon, JS)散度所存在的问题。当两个分布不存在重叠时,JS散度不能为生成器提供连续有效的梯度而导致模型失效。因此采用Wassertein距离去衡量生成数据分布和真实数据分布之间的距离,以解决训练不稳定的问题。此时损失函数变为:

(4)

其中,L是1-Lipschitz函数。则判别器损失函数改写为:

JD=-Ex～pdata(x)[D(x)]+Ez～pz(z){D[G(z)]}

(5)

生成器的损失函数改为:

JG=-Ez～pz(z){D[G(z)]}λ

(6)

WGAN极大地优化了GAN中出现的问题,但是为了使用Wassertein距离,WGAN需要对判别器权重WD进行裁剪,使它在一定的范围(-c,c)内。其对权重进行裁剪的做法过于粗暴,这一操作间接限制了其梯度信息发生,并且对训练的稳定性造成伤害。针对这一问题,WGAN-GP提出用梯度惩罚机制代替权重裁剪,将判别器的损失函数更改为:

JD=Ez～pz(z){D[G(z)]}-Ex～pdata(x)[D(x)]+

(7)

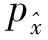
WGAN-GP进一步稳定了GAN的训练过程,而且保证了结果质量,因此本文采用WGAN-GP的损失函数设计预训练网络。

WGAN-GP的结构如图3所示。其中fc是全连接层,将200维的噪音输入映射为256维。

本文采用所有的无标签样本用来训练WGAN-GP网络,得到训练好的生成器和判别器参数模型。

2.2 半监督调制信号识别模型

WGAN-GP网络具有良好的训练稳定性,但它是无监督模型,其判别器部分是一个二分类器,只判断输入数据的真假,并不能直接用于多种信号的调制识别。为此需要对网络结构进行改进,使其既保留WGAN-GP利用无类别标签数据学习提取特征的能力,又能获得信号分类能力。

在WGAN-GP的基础上,本文设计了一种半监督模型架构,即SSGAN-2D,如图4所示。SSGAN-2D的分类器将接收三种数据,分别是由WGAN-GP中生成器接收噪声生成的伪数据、有类别标签的真实数据和无类别标签的真实数据。

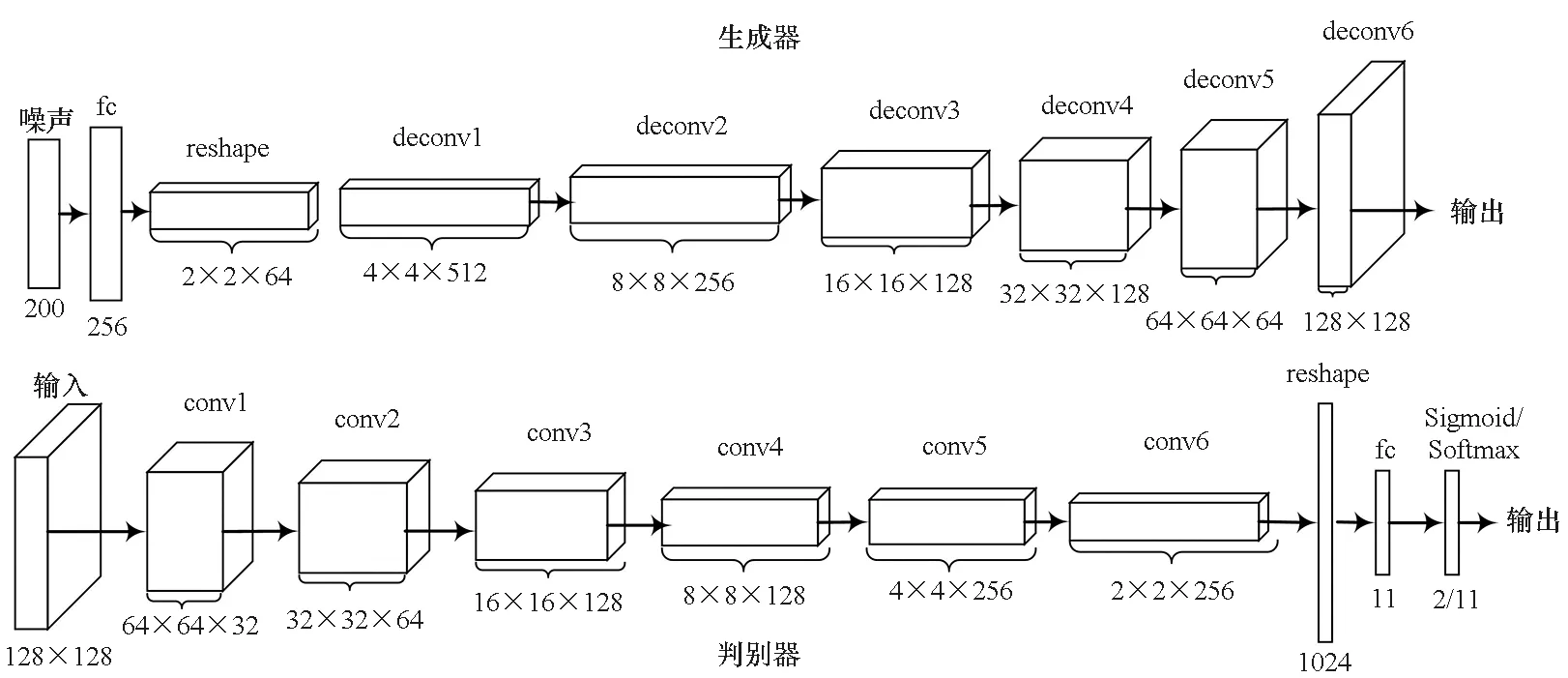
图3 WGAN-GP网络结构Fig.3 WGAN-GP network structure

图4 半监督调制信号识别模型: SSGAN-2D Fig.4 Semi-supervised modulation signal recognition model: SSGAN-2D

假设数据共k类,将输入判别器数据的真伪看成第k+1类,是为1,不是则为0。这样,将Generator生成的伪数据的标签设置为unlabel_f={0,0,0,…,1}(前k项为0,k+1项为1),无标记的真实数据的标签设置为unlabel_r={1,1,1,…,0},有标记的真实数据的标签为label_r={y1,y2,y3,…,0}(前k项表示真实的类别标签)。这样,所有数据的标签都变成k+1维。在Softmax分类器判别时,由生成器产生的伪数据unlabel_f={0,0,0,…,1}和无标记真实数据unlabel_r={1,1,1,…,0}仍是一个二分类问题(标签前k维看作一部分,第k+1维看作一部分,就是简单的0,1二分类标签),从而得以实现原始GAN无监督提取特征的能力。而对有标记的真实数据来说,其标签第k+1维添加的0并不影响其分类。这样则统一了无监督模式和监督模式的分类器输出。

SSGAN-2D中,生成器损失函数和WGAN-GP是一样的,即:

LG=-Ez～pz(z)(lg{D[G(z)]})

(8)

而SSGAN-2D中的判别器的损失函数既包括有监督损失又包括无监督损失。在接收有标记样本时,优化有监督损失Lsupervised,在接收无标记真实样本时,优化无监督损失Lunsupervised,总损失函数LD=Lsupervised·(1-flag)·10+Lunsupervised,flag是一个表征输入数据是有类别标注(取0)或无类别标注(取1)的标志符。取0时,LD=Lsupervised×10+Lunsupervised,其中Lsupervised乘以10后远大于Lunsupervised,从而主要优化的就是有监督损失部分;取1时,LD=Lunsupervised,优化无监督损失部分。这两部分的具体函数分别为:

Lsupervised=-Ex,y～pdata(x,y)lg[px(y=ix,y

(9)

Lunsupervised=-{Ex～pdata(x)lg[1-px(y=k+1x)]+

Ex～Glg[px(y=k+1x)]}

(10)

其中,px(y=ix,y

3 实验和分析

为了验证提出的基于SSGAN-2D模型的调制信号识别方法,在公开数据集RADIOML 2016.04C.上进行实验验证,并和卷积神经网络方法进行比较。该数据集包含11类调制样式:8PSK, AM-DSB, AM-SSB, BPSK, CPFSK, GFSK, PAM4, QAM16, QAM64, QPSK, WBFM。信噪比范围为[-20,18]dB,间隔为2 dB,信号为双通道2×128维度,每种信噪比包含8 103个样本。

3.1 实验1:不同带标签样本个数对半监督识别结果的影响

针对不同带标签样本个数的数据集分别进行算法验证:

选择信噪比为12 dB的信号进行试验,随机选择50%的数据作为训练样本,另外50%的数据作为测试样本。为了挑战所提算法的能力,本文从训练样本中随机挑选数量从110～1 100(11类信号,每类信号数目相同)的多组数据作为有标签数据,剩余数据作为无标签数据,来开展试验。

利用有标签数据进行识别模型训练的卷积神经网络方法作为对比。为了保证对比效果的客观性,卷积神经网络结构和SSGAN-2D中的判别器基本一致,不同的是,输出为11类。具体识别准确率实验结果如表1所示。

表1 不同带标签样本数量条件下的识别准确率实验结果

实验结果表明:在不同带标签样本个数条件下,本文所提的SSGAN-2D方法能很好地利用无标签数据,辅助特征提取,从而获得比CNN方法更好的识别效果。进一步地,当带标签数据较少时,SSGAN-2D方法的优势较大,而随着带标签数据的增多,SSGAN-2D方法的优势会逐渐减少,这个现象是可以理解的。当带标签数据较少时,CNN不能很好地训练,无法得到较好的信号特征,而半监督模型可以利用大量无标签数据辅助完成信号特征的提取;当带标签相对较多时,CNN方法本身就能提取较好的、用于准确识别的信号特征,半监督模型能利用无标签数据的优势反而不明显。

3.2 实验2:不同信噪比对半监督识别结果的影响

针对不同信噪比的数据集分别进行算法验证:

选取了0 dB, 8 dB, 10 dB, 12 dB, 14 dB, 16 dB, 18 dB共7种信噪比的信号数据分别进行实验。每种信噪比的信号数据中随机选择50%的数据作为训练样本,另外50%的数据作为测试样本,半监督算法的主要兴趣是针对小样本数据进行处理,所以本文把有标签数据样本的数量设定为440(每类样本数量均为40),剩余数据作为无标签数据,开展实验。

具体识别准确率实验结果如表2所示。从表2

表2 不同信噪比条件下的识别准确率实验结果

中可以看出,在有标签样本数量极端少,每类只有40个时,SSGAN-2D方法同样表现出了强大的性能。在信噪比为12 dB时,SSGAN-2D方法达到最高的识别准确度为90.7%,在不同信噪比条件下,SSGAN-2D方法和CNN方法相比,都有明显的优势。

在实验过程中发现,当有标签样本数量较少时,信号识别率和样本选择强相关,如果选择的样本较好地反映了样本集分布,则识别率较高,反之,识别率较低。而这也是符合常理的。所以,为了反映算法效果的客观性,上述两个实验中,针对同一标签数量,均随机选择样本进行10次识别实验,并取识别率均值,作为最终识别结果。

4 结论

GAN因为其强大的逼真样本生成能力已被成功应用到众多领域,本文将其应用在调制信号识别问题上。对通信信号进行了一种冗余空域变换,使其在适应生成对抗网络模型的同时保留丰富的信号相邻特征;设计了一种基于生成对抗网络且适宜电磁信号处理的半监督学习框架,实现了弱监督条件下调制信号的端到端调制识别。结果表明,所提方法在有标签数据较少的情况下,能很好地利用无标签数据辅助特征提取,获得比当前几乎最优的卷积神经网络方法更好的识别效果。

后期,还将对SSGAN-2D中生成器及判别器结构设计、计算复杂度降低、训练稳定性增强、损失函数优化等方面进行进一步探索,以期获得更好的表现。