集成平台空域辅助阵列共址干扰抑制技术
李 彤,潘文生,邵士海,杜林松,时成哲
(电子科技大学 通信抗干扰技术国家级重点实验室, 四川 成都 611731)
集成平台搭载多个用频设备,以机载、车载、舰载平台为例,在有限空间中,用频设备之间由于频段重叠,同时工作时,本地发射设备会对接收设备产生严重的共址干扰,造成接收设备空口饱和,无法正常工作。目前,共址干扰空域抑制方法主要分为两类:被动无源和主动有源空域共址干扰抑制[1-4]。
被动无源空域共址干扰抑制,使用器件或天线的固有特征,包括自然隔离或障碍物阻挡、电磁波传输的空间损耗、天线极化方式等[5]。主动有源空域共址干扰抑制方法主要利用波束成形等技术,通过对多根天线接收或发送的信号进行幅度和相位调整,形成规定指向上的波束样式[6]。
在多发多收场景中,通常采用主动有源空域共址干扰抑制方法。文献[7-8]采用发射机和接收机联合波束成形的方法,在接收机处形成零陷区域进行干扰抑制。文献[9]利用零空间投影和左零空间投影的方法,在正交的子空间上实现空分同时同频全双工。文献[10]提出了一种基于角度的多级混合预编码方法,通过在发射机和接收机处进行多级预编码提升干扰抑制性能,最大化目标信号功率,减小信道估计开销和硬件实现难度。
在上述研究中,发射机和接收机波束成形方法需要收发设备距离相对较远,而在集成平台环境下,收发设备之间距离较近,旁瓣干扰明显。除此之外,接收机波束成形需要将各个天线接收信号在射频或数字域进行叠加抵消,集成平台环境下,强大的共址干扰会使得接收设备处天线空口饱和,造成接收设备无法正常接收信号,不能有效抵消干扰。零空间向量等方法需要干扰源处发射阵列使用特定的预编码方式,该方法对信道条件有所要求且会影响到发射设备的传输效率[11]。
针对集成平台中共址干扰导致空口饱和的问题,在不限制本地收发设备发射和接收方式的情况下,提出了一种利用辅助阵列抵消共址干扰的方法。首先,建立了增加辅助阵列后的接收信号模型,对辅助阵列权值向量进行优化,推导了最小残余干扰功率表达式。其次,提出了共址干扰空域完美抵消需要满足的信道条件,建立远、近场信道模型,分析了主发射阵列非合作情况下,辅助阵列摆放位置,以及主发射阵列合作情况下,二者位置的相对关系。最后,推导了非完美抵消信道条件下的干扰抑制比(self-interference cancellation ratio, SICR),并分析了干扰抑制比的影响因素。
1 系统模型
为了解决接收设备天线空口饱和问题,考虑通过在接收设备端增加辅助阵列,利用其发射信号在接收设备阵列空口处抵消共址干扰,使接收设备能够正常工作。
平台中发射阵列分为两部分:主发射阵列和辅助阵列。主发射阵列用于向远端接收机发射信号,辅助阵列用于空域抵消主发射阵列发射信号对本地接收设备的影响。
此时,接收阵列天线空口处接收信号可以表示为
(1)
式中,L1和L2分别表示主发射阵列与辅助阵列到本地接收阵列的信道矩阵,H为远端发射机到本地接收机的信道矩阵,w1、w2和wt分别为主发射阵列、辅助阵列与远端发射阵列的调节幅相的权值向量,x和y分别表示本地发射机与远端发射机的发射信号,n为加性噪声。
接收信号的功率为
(2)
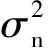
通过调节辅助阵列发射权值向量w2,使得残余干扰信号功率最小,该优化问题可以表示为
(3)
该优化问题最小范数条件下的最优解为
(4)
式中,(·)+表示广义逆矩阵。
假设L2的奇异分解为L2=UDV,则残余干扰功率最优值可以表示为

(5)
式中,r为L2的秩,Nr为接收天线个数,(·)H表示共轭转置矩阵,IN表示N维单位矩阵,0M×N表示M×N维零矩阵。
由式(5)可以看出,每增加一个辅助阵列到接收阵列的信道自由度,就能减少一个主发射天线到接收天线阵列的自由度,当辅助阵列到接收阵列的信道自由度达到最大时,无论本地发射阵列到接收阵列的信道如何,权值向量如何,均能在接收阵列处抵消共址干扰。
2 共址干扰空域完美抵消的信道条件

2.1 主发射阵列位置非合作
条件1∀L1∈Nr×Nt,1,∀w1∈Nt,1×1,∃w2∈Nt,2×1,使则L2需满足rank(L2)=Nr。
证明:
∀L1∈Nr×Nt,1,∀w1∈Nt,1×1
⟺∀a∈Nr×1
⟺rank(L2)=Nr
(6)
其中,rank(·)表示矩阵的秩。
□
辅助阵列到接收阵列的信道矩阵可以表示为
L2=A2∘E2
(7)
式中,A2表示辅助阵列到接收阵列的路径衰减,E2表示辅助阵列到接收阵列的相位偏差,“∘ ”表示Hadamard积。
定理对于矩阵A∈m×n,E∈m×n,其Hadamard积为L=A∘E,则在概率意义上
rank(E)=m⟹rank(L)=m
(8)

(9)
当m=2时,
(10)
式中,|·=det(·)表示矩阵的行列式。
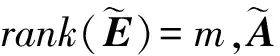
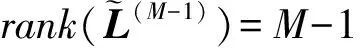
当m=M时,
(11)
(12)
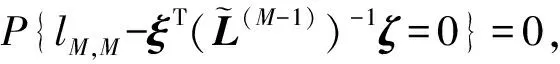
同理可证以下推论。
□
推论对于矩阵A∈m×n,E∈m×n,其Hadamard积为L=A∘E。
rank(A)=m⟹rank(L)=m
(13)
由定理和推论可以看出,只需rank(E2)=Nr或rank(A2)=Nr,即可使得rank(L2)=Nr。此时,无论主发射阵列到接收阵列信道如何,权值向量如何,均可将共址干扰完美抵消。
2.1.1 远场场景
考虑辅助阵列与接收阵列均为均匀线阵,远场场景下,采用平面波模型,辅助阵列到接收阵列的信道由辅助阵列出射波束和接收阵列入射波束的方向角决定。
此时,辅助阵列到接收阵列的相位矩阵可以表示为
E2=er,2(Ωr,2)[et,2(Ωt,2)]T
(14)
(15)
(16)
其中:er,2(Ωr,2)为沿Ωr,2方向的接收单位空间特征图,er,2(Ωr,2)∈Nr×1;et,2(Ωt,2)为沿Ωt,2方向的发射单位空间特征图,为向量er,2(Ωr,2)中第nr个元素;为向量et,2(Ωt,2)中第nt,2个元素;Ωr,2=cosφr,2,Ωt,2=cosφt,2;Δ为归一化发射接收天线间隔;φt,2和φr,2分别为辅助阵列与接收阵列处视距路径的出射和入射角;(·)T表示转置矩阵。
由于辅助阵列位于接收阵列远场位置,在平面波模型下,每一个辅助发射阵元到接收阵元的路径衰减均相等,记为a,那么,辅助阵列到接收阵列的信道矩阵可以表示为
L2=A2∘E2=aE2=aer,2(Ωr,2)[et,2(Ωt,2)]T
(17)
由式(17)可以看出,信道矩阵为秩1矩阵,当且仅当接收阵列天线数为1时,满足条件1。
2.1.2 近场场景
考虑辅助阵列与接收阵列均为均匀线阵,近场场景下,采用球面波模型,辅助阵列到接收阵列的信道由阵元间距离决定。考虑辅助阵列与接收阵列近场摆放位置如图1所示。

图1 辅助阵列与接收阵列近场摆放位置Fig.1 Near field location of auxiliary array and receive array

(18)
(19)
(20)
其中,θ2为辅助阵列与接收阵列之间的夹角,D2为辅助阵列与接收阵列之间的距离。
假设D2≫D,D为阵列尺寸,使用与文献[12-13]相同的近似,阵元间距离可以表示为
d(2)(nr,nt,2)≈[(nt,2-1)Δλcosθ2+D2+(Nr-nr)Δλ]·
(21)
下面考察满足条件1,即rank(L2)=Nr时,各变量之间需满足的关系。
由定理可知,只需使rank(E2)=Nr,即可满足条件1。
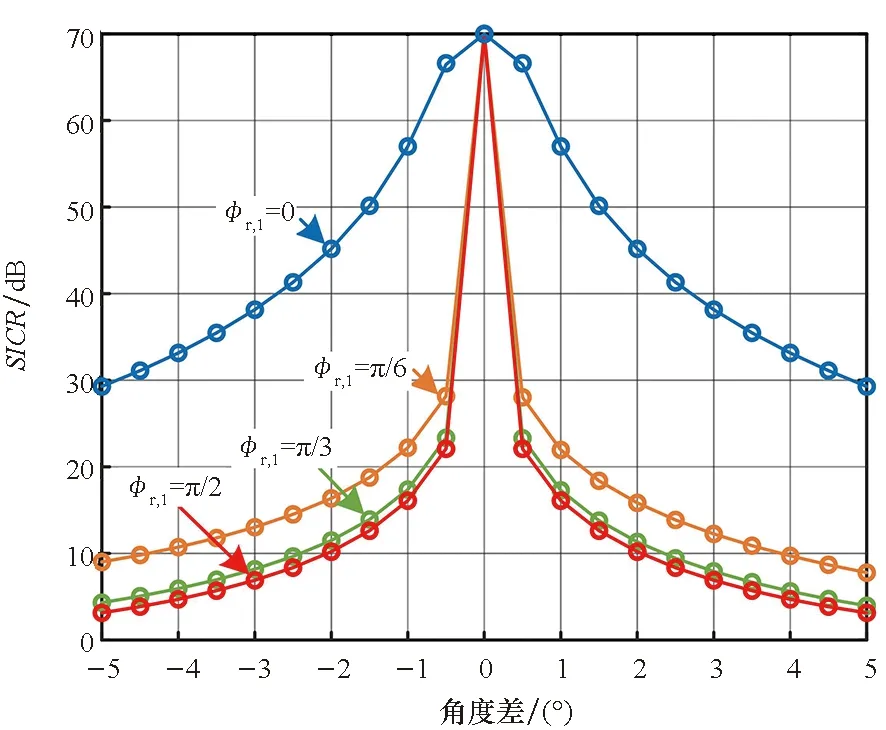
1)当Nt,2 rank(E2)≤min(Nt,2,Nr)=Nt,2 2)当Nt,2=Nr时: ①当Nt,2=Nr=1时,rank(E2)=1=Nr成立。 ②当Nt,2=Nr≥2时 (22) 式中, (23) (24) ≠2kπ,k∈,1≤nt,2 (25) 由于D2≫D,因此只要sinθ2≠0,即能满足条件1。 3)当Nt,2>Nr时: 辅助阵列到接收阵列的信道相位矩阵可以表示为 (26) ①当sinθ2=0时, (27) 式中,βnt,2=exp{-j2π[D2+(Nr+nt,2-2)Δ]},lnr=exp(j2πΔ)。 可以看出,E2是一个秩为1的矩阵,当且仅当Nr=1时,满足条件1。 综上所述,可以得到以下结论: 1)当辅助阵列位于远场: 当且仅当Nr=1时,可以满足条件1。 2)当辅助阵列位于近场: ①Nr=1、Nt,2≥1时,满足条件1。 ②Nt,2≥Nr且sinθ2≠0时,满足条件1。 条件2∀w1∈Nt,1×1,∃w2∈Nt,2×1,使则需满足L1=L2T。 证明:由于U为Nr维酉矩阵,可以将L1表示为L1=UP,其中P∈Nr×Nt,1。 ∀w1∈Nt,1×1 =L2T (28) □ 当辅助阵列位于近场时,可以通过位置摆放达到共址干扰完美抑制。因此,仅在辅助阵列位于远场位置时,考虑主发射阵列位置合作方式。此时,主发射阵列到接收阵列的信道矩阵需要满足条件2,即 L1=L2T=aer,2(Ωr,2)[et,2(Ωt,2)]TT =aer,2(Ωr,2)ηT (29) 式中,η=TTet,2(Ωt,2)∈Nt,1×1可为任意向量。 由矩阵L1构造可知,主发射阵列应位于接收阵列远场区域,且辅助阵列与主发射阵列发射信号到达接收阵列的入射角应相等。 (30) 最大干扰抑制比可以表示为 (31) 由式(31)可以看出,在主发射阵列位置非合作情况下,干扰抑制比随接收阵元数的增加而减小,随辅助阵列到接收阵列信道矩阵的秩增大而增大。当辅助阵列位于接收阵列近场且辅助阵元数小于接收阵元数时,辅助阵列到接收阵列信道矩阵的秩等于辅助阵元数,因此,干扰抑制比随辅助阵元数增加而增大;当辅助阵元数大于等于接收阵元数时,干扰抑制比达到最大值,不随辅助阵元数的变化而变化。 (32) 最大干扰抑制比可以表示为 (33) 式中, (34) 由式(33)可以看出,在主发射阵列位置合作情况下,考虑主发射和辅助阵列均位于接收阵列远场场景,干扰抑制比随主发射阵列和辅助阵列发射信号在接收阵列处的入射角度差的增大而增大。 图2给出了近场场景不同摆放角度下,辅助阵列天线数量与干扰抑制比的关系。可以发现,仿真曲线与理论推导曲线相一致,当辅助阵列天线数大于接收阵列天线数且摆放角度不为0时,共址干扰可以被完美抵消,验证了第2节中的结论。当摆放角度不为0时,干扰抑制比随着辅助阵列天线数的增加而增大,当摆放角度为0时,干扰抑制比不变。这是因为摆放角度不为0时,辅助阵列天线数即为信道矩阵的秩,当辅助阵列天线数增加时,辅助阵列到接收阵列的信道空间自由度增加,能够更大程度地减少主发射阵列的分集,从而更好地抵消干扰。然而,当摆放角度为0时,辅助阵列天线数增加,信道自由度不发生变化,因此干扰抑制比不变。 图2 辅助阵列天线数量与干扰抑制比的关系Fig.2 Relationship between number of auxiliary array and SICR 图3给出了远场场景主发射阵列合作情况下,辅助阵列和主发射阵列发射信号在接收阵列处入射角度差值与干扰抵制比的关系,其中,“○”表示仿真结果,“—”表示理论结果。可以发现,仿真曲线与理论推导曲线相一致,当辅助阵列与主发射阵列发射信号在接收阵列处具有相同入射角时,共址干扰可以被完美抵消,验证了第2节中的结论。当入射角度差不为0°时,干扰抑制比随着角度差的增大而减小,随着主发射阵列入射角度的增大而减小。 图3 入射角度差与干扰抑制比的关系Fig.3 Relationship between incident angle difference and SICR 本文提出了一种利用辅助阵列抵消共址干扰的方法,利用辅助阵列发射信号在接收阵列空口处对共址干扰进行抵消。首先,建立了共址干扰抵消后的接收信号模型,推导了最小残余干扰功率表达式。其次,提出了共址干扰空域完美抵消需要满足的信道条件,分析了主发射阵列非合作情况下,辅助阵列摆放位置,以及主发射阵列合作情况下,二者位置的相对关系。当辅助阵列位于接收阵列近场时,无须主发射阵列合作即可有效抵消共址干扰;当辅助阵列位于远场时,需要主发射阵列合作,当二者发射信号到达接收阵列的入射角度相同时,可以完美抵消共址干扰。最后,推导了不完美抵消信道条件下的干扰抑制比,并分析了干扰抑制比的影响因素。理论与仿真结果表明,采用辅助阵列空域共址干扰抑制的方法可以在空口处有效抑制共址干扰,且不影响本地发射机的传输效率。

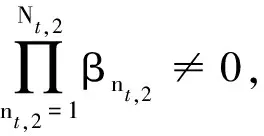
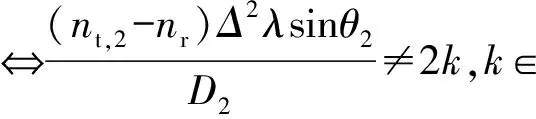
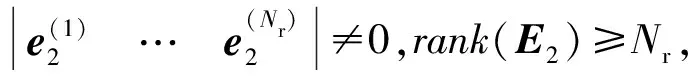
2.2 主发射阵列位置合作
3 不完美信道条件下的干扰抑制比
3.1 主发射阵列位置非合作

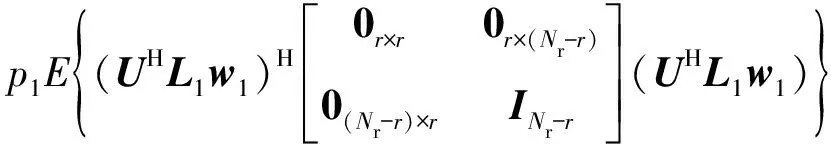

3.2 主发射阵列位置合作
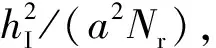

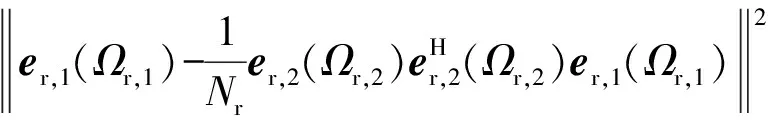

4 系统仿真与性能分析
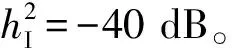

5 结论

