基于遗传算法的装备小修维修人力资源配置优化

曹军海,刘 振†,胡亚俊,丁思源

(1. 陆军装甲兵学院,北京 100071;2. 中国人民解放军92057部队,广东 湛江 524000)

在新体制下,陆军合成部队主要承担以换件修理为主、原件修理为辅的装甲装备小修任务[1-2]。装甲装备结构复杂,小修工序数量较多,涉及诸多专业,且工序难易程度差异较大,整个维修作业流程是包含多条并行作业线的维修网络形态[3-6],在这一过程中如何科学地调配维修人力资源,提高小修工作效率,以满足因装备训练增多而日益增长的装备维修任务需求,提高装备可用度和完好率,是基层部队装备保障领域的研究热点之一[7-9]。

在研究部队装备维修车间维修作业中人力资源配置问题时,随着工序数量的增加,维修工序的资源配置方案数量呈指数级增长,很难在短时间内穷举所有的配置方案。一些学者通过应用或改进元启发式优化算法对装备维修保障资源的配置策略优化进行研究,如遗传算法、蚁群算法和粒子群算法等[10-12]。刘文宝等[13]在装备维修工序顺序固定的基础上,利用遗传算法来求解装备维修任务的规划问题,而在实际维修保障作业中,部分工序在无资源冲突的情况下也可以采取并行方式开展维修作业,即在维修工分配策略不同时,实际产生的工序流程也会有所不同。张宏远等[14]采用免疫算法对装备大修的维修人员配置问题进行了研究,问题假设中只考虑了单道工序仅由一名维修工负责的简单情况,由于工序作业的难易程度有差异,单道工序也可能由多名维修工共同作业完成。基于以上考虑,本文以维修人员配置均衡度最高且装备维修总工期尽可能短为优化目标,研究在部队装备维修车间中带有工序顺序关系的并行流水线条件下进行装备小修时,维修人力资源的最优调配方案。

1 装备小修作业流程分析

装甲装备小修属于预防性维修,主要以装备发动机摩托小时消耗或行驶里程数为标准,对装备进行定期维修。陆军合成部队装备小修作业平时主要依托队属装备维修车间展开,维修一台装甲装备,通常由一个维修班组负责,且以装备底盘修理为主,上装分系统视情况进行检修。自装备接车清洗到修竣交车,要经历拆卸、检测、修理、组装、测试等数百道可更换单元(LRU)级维修工序,并且修理过程中各工序有明确的顺序关系。同时,对于不同型号的武器装备,其维修工序流程也存在差异。

维修人力资源的专业与维修工序的专业要求相对应(见图1),维修人力资源根据专业的不同,可以划分为底盘、武器、火控、通信、电子、防护等修理专业。另外,维修人员依据技术等级的不同,划分为初级、中级、高级等,不同技术等级的维修工的维修技能熟练程度不同,在实际维修作业中表现为参与维修相同工序耗费时间的不同。

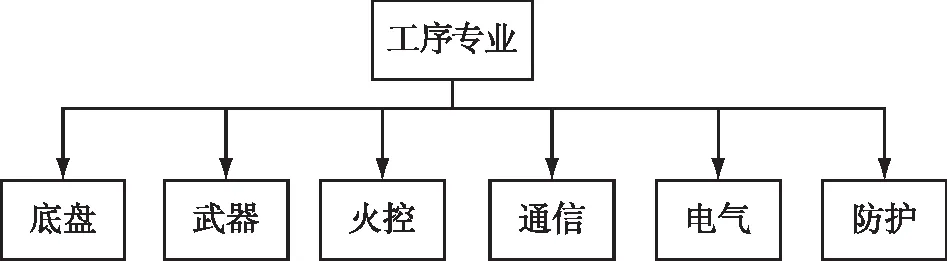
图1 装备小修工序专业划分示意Fig.1 Schematic diagram of major division of equipment minor repair process

2 装备小修作业人力资源配置问题建模

2.1 问题描述

考虑实际装备小修作业过程中,维修车间内有多条修理作业流水线,具备开展并行维修作业的空间条件。同时,装备小修中底盘修理专业是占用维修工最多的,而武器、火控、通信等上装专业需要的维修工往往数量较少,对其资源配置进行优化的必要性不大,因此本文重点研究单台装甲装备进行小修作业时,底盘维修工如何配置,使得维修工配置均衡合理且装备维修总工期尽可能短。

2.2 问题假设

1)维修车间内设备和维修可更换备件资源充足,不存在资源分配冲突;

2)待小修的装备,经修前检测后,可以确定预防性维修具体项目,即标准的工序顺序已知;

3)单台装备由一组维修工负责,记录的维修工作业时间是连续的(除维修作业外,训练、学习、休息的时间不计入),当天未完成的工序在下一天继续进行;

4)在维修作业未完成上一工序任务前,保障资源一直被占用,待完成当前工序任务后,资源被释放;同一资源不能同时完成两项或以上的工序任务;前后工序衔接时间很短,忽略不计。

2.3 符号表示

为方便模型表示,明确如下符号含义。如表1所示。

表1 符号表示Tab.1 symbolic representation

2.4 维修人力资源配置问题建模

维修工配置的总评价指标由装备维修总工期和维修工配置工作强度均衡度(以下简称配置均衡度)构成,其中,装备维修总工期为装备第一道维修工序开始到最后一道工序结束所经历的时间,维修工配置均衡度指标用维修工工作负荷的标准差表示。分别将m道维修工序和n名维修人员进行编号,W={1,2,…,i,…,m},R={1,2,…,i,…,n},建立优化目标函数和约束条件如下:

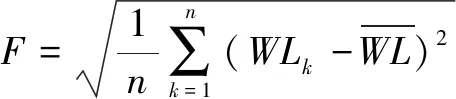
(1)

s.t.
∑∑Rij=n

(2)

∑Wi=m

(3)

Pj≥Nj

(4)

Ts,j=Te,i,WPij=1

(5)

其中,式(1)为优化目标函数,ω为权重超参数,取值范围在0～1。工作负荷WLk,用当前维修工进行装备维修各工序所花费时间与相应工序劳动强度乘积之和来表示,通过计算工作负荷的标准差来找到各维修工工作强度差异较小的资源配置方案。

3 维修人力资源配置优化算法设计

遗传算法借用了进化论中“适者生存”的观点,本质是一种并行、高效、全局搜索的算法,从某一初始种群开始,通过选择、交叉和变异操作,使种群不断进化到搜索空间更优的区域,最终收敛到更适应环境的个体,得到问题最优解。按照“生成初始维修资源配置方案种群-更新维修网络流程-适应度计算-遗传进化”的步骤,对维修人力资源配置优化的遗传算法进行设计,如图2所示。

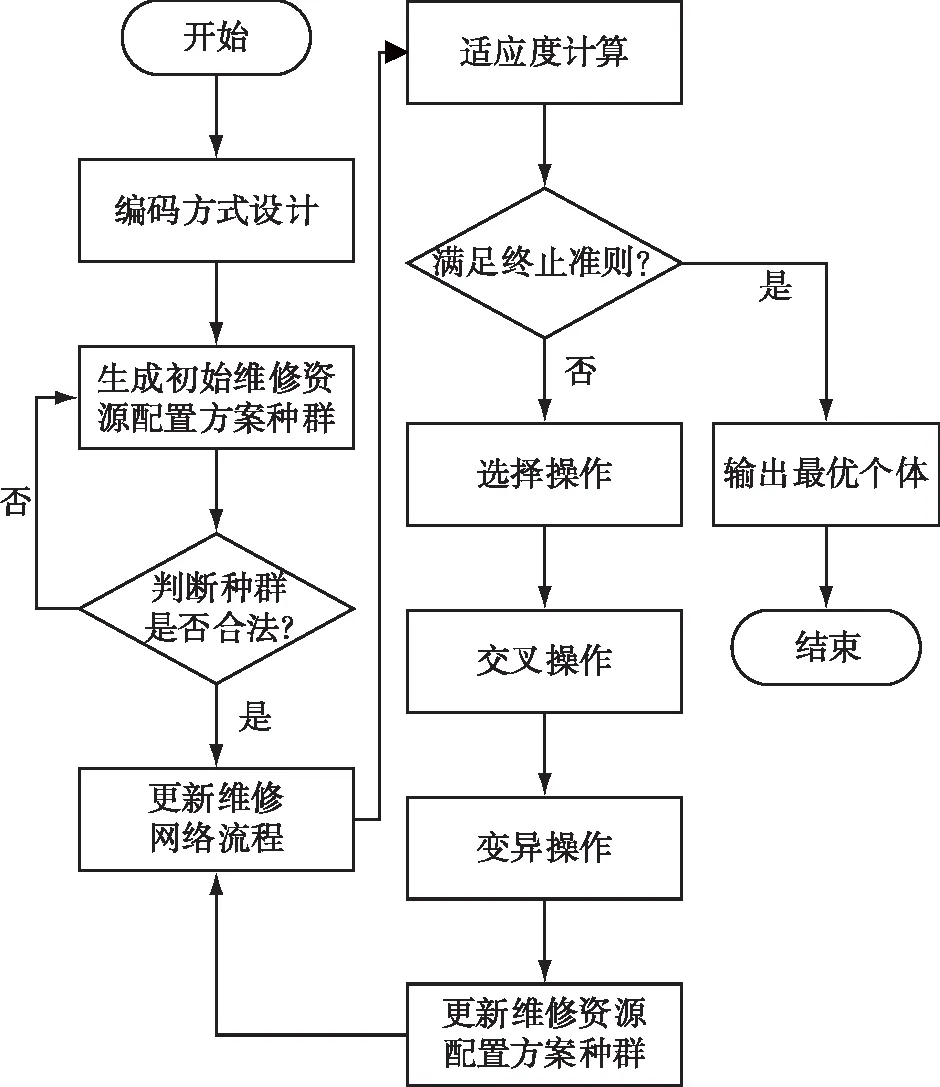
图2 遗传算法步骤Fig.2 Genetic algorithm steps

3.1 编码方式与适应度函数设计

本文遗传算法的适应度函数与数学模型目标函数保持一致,算法中个体表示某一维修保障资源配置方案,众多个体组成种群,个体中染色体编码采用二进制矩阵形式,如表2所示,一串染色体序列表示有m个维修工序、n个维修工,编为m*n的矩阵,每行代表一道维修工序,每列代表该维修工的分配情况。其中位置元素1表示将该名维修工分配给该工序,0表示不予分配。

表2 维修工分配编码矩阵Tab.2 Maintenance worker assignment coding matrix

3.2 初始信息设置与初始种群生成

构建维修工序与维修工映射矩阵,如表3所示,可以描述工序需要的维修工专业、需求人数、历史维修完成时间及工序劳动强度等信息,其中用1-n的整数表示维修工专业类别。根据GJB 1336-92对军事体力劳动强度的分级,将维修工序的劳动强度分为轻、中、重、很重、极重,用整数1-5分别表示,并赋予一定权重,如表4所示。

表3 工序-维修工对应矩阵Tab.3 Process-Maintenance worker correspondence matrix

表4 劳动强度权重Tab.4 Labour intensity weight

另外,不同技术等级的维修人员对应着同一道维修工序的维修工时不同,根据维修工技术等级情况确定权重系数,从而计算各工序维修过程占用的时间,如表5所示。

表5 技术等级权重Tab.5 Technical grade weight

根据上述初始信息,随机生成维修工配置方案初始种群,判断资源分配方案是否符合工序工种和需求人数要求,若符合要求,即为合法种群;否则,重新生成种群。

3.3 维修网络流程更新

装备小修的标准作业流程是针对理想条件且不存在人力资源限制情况下的维修作业流程,而在实际工作中,由于实际配置的人力资源有限且会变化,考虑小修作业流程中并行工序流程会受到工序前后顺序和维修人力资源实际配置方案的多重影响,实际维修流程会与标准工序流程有所不同,本文提出了一种基于禁忌表的维修网络流程更新算法,可以根据工序顺序关系和资源配置方案,自动确定实际的维修网络流程。以下步骤中,以当前正在进行的所有工序完成时间的最小值为仿真时钟下一步的推进位置,算法的基本步骤如图3所示。

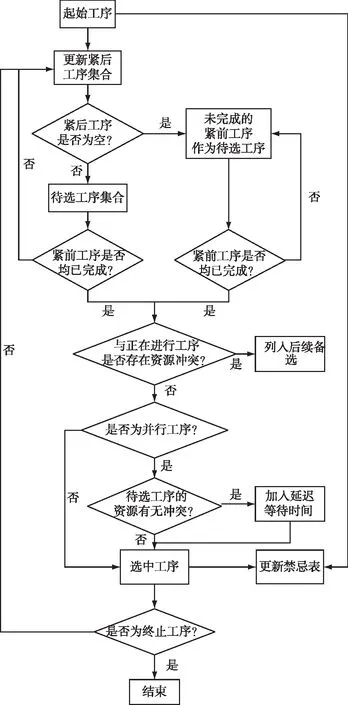
图3 维修网络流程更新算法Fig.3 Maintenance network process update algorithm

3.4 遗传进化操作

1)基于轮盘赌的选择操作[15]。首先,对种群中的个体适应度值进行去中心化计算,再利用每个个体适应度所占比例进行轮盘赌选择,从而复制选择出的个体作为父代个体。fitvalue=fitness/∑fitness,其中fitness=(max(f)-fi)/(max(f)-min(f)),f为当前迭代次数下种群的适应度值集合,fi为第i项个体的适应度。

2)基于概率的交叉操作。如图4所示,随机选择染色体矩阵中的若干行,以交叉概率选中两个父代,对染色体矩阵相对应的行位置与另一个父代进行相应行位置交换,以产生新的个体。

图4 染色体矩阵交叉过程Fig.4 Chromosome matrix crossing process

3)基于概率的变异操作。如图5所示,以变异概率选中的单个父代,随机选择一个工序工种,把该工序工种的所有对应行位置按照工序专业及需求人数要求进行重新编码,确保产生新的合法子代个体。

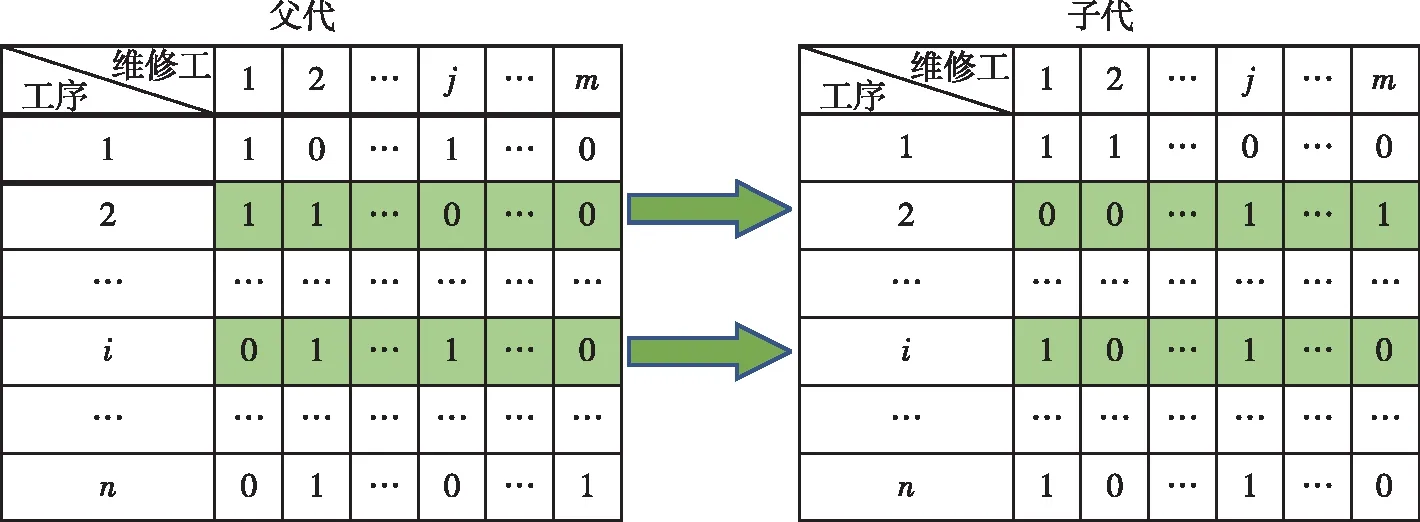
图5 染色体矩阵变异过程Fig.5 Chromosome matrix variation process

4 算例分析

4.1 算例描述

某部修理连现有一组底盘专业(A)维修工8名在位,另有10名上装维修工,专业分别为B、C、D、E、F,相应专业的维修工数量分别为2、2、2、2、2(名),具体维修工技术等级情况见表6。现需对单台某型号装甲装备进行小修,基于已知工序对8名底盘维修工进行配置,使维修工配置均衡度最高且装备维修总工期尽可能短。

表6 维修工基本情况Tab.6 Basic information of maintenance workers

该装备小修标准流程有85道工序,工序顺序关系如图6。

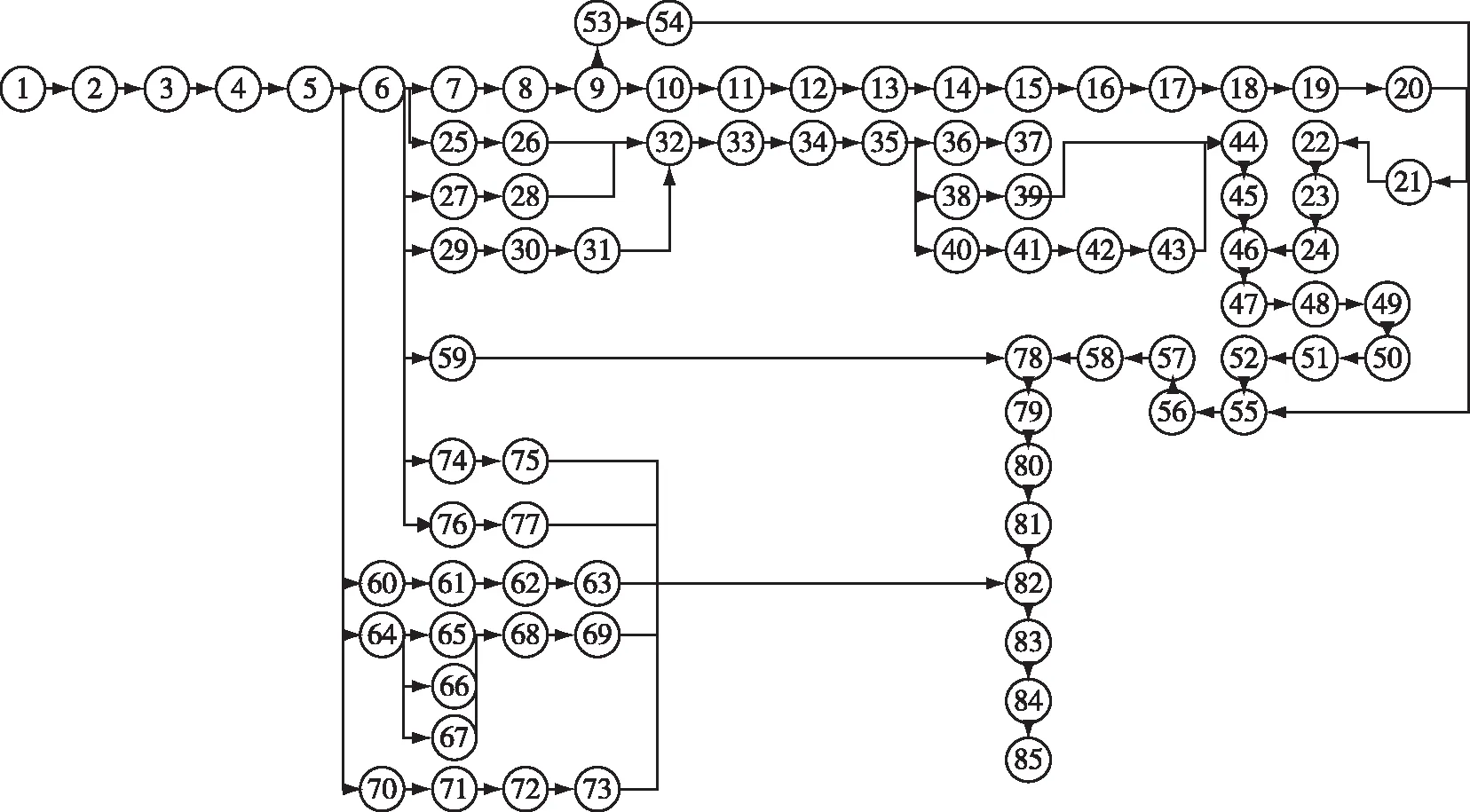
图6 装备小修工序流程Fig.6 Equipment minor repair process flow

为方便计算结果分析,现将某合成部队中拥有初级技术等级的维修人员对应工序的历年维修完成时间的统计均值,作为相应工序平均完成时间,各工序相关信息如表7所示。

表7 工序相关数据Tab.7 Process related data

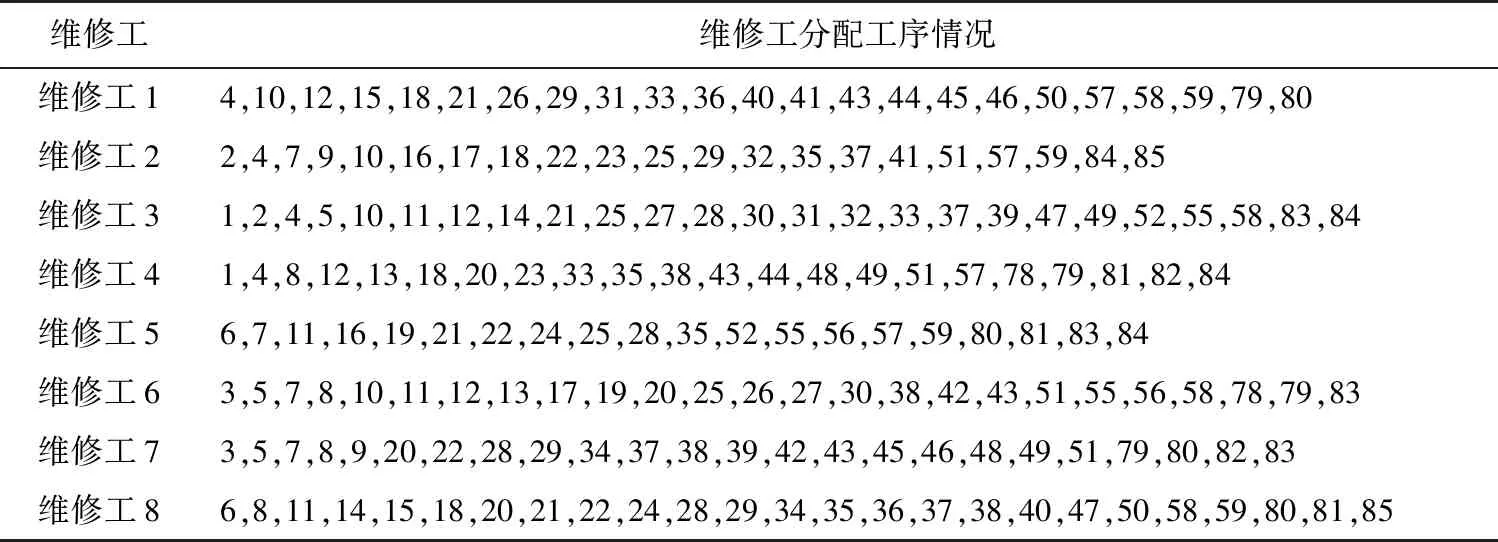
表8 维修工最优分配方案

4.2 仿真分析

仿真实验使用Matlab软件进行遗传算法编程,染色体采用二进制矩阵编码方式,用85*18的矩阵表示维修人力资源在工序作业中的配置方案。种群大小NP=50,遗传迭代次数G=500,交叉概率Pc=0.9,变异概率Pm=0.1,ω=0.4。考虑单条流水线(串行工序)和多条流水线(并行工序)两种作业方式分别进行仿真实验。通过运行计算发现,随着迭代次数增加,最优适应度随之减少,最终收敛性稳定。采用该遗传算法在串行工序和并行工序作业条件下均能得到底盘专业最优维修工配置方案,如图7所示。

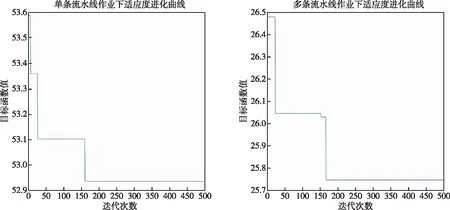
图7 遗传算法迭代曲线Fig.7 Iterative curve of genetic algorithm

在多条流水线作业下,求得的最优维修工配置方案,维修工配置均衡度为2.216 3,装备维修总工期为61.041 7 h。通过维修工-维修时间甘特图(见图8)可以看出,维修工工作强度分配均衡合理。根据该装备小修历史数据,单台该装备的维修工期为半个月,排除掉进行维修工作之外的训练、休息等时间,历史维修工期约80 h,优化后的维修时间缩短了23.7%,取得较显著的优化效果。

5 结束语

装备维修作业流程中人力资源的优化问题是部队装备保障能力建设的重要研究领域,如何提高维修作业效率同时均衡人力资源工作强度,是该优化问题的基本目标。本文针对陆军部队装备维修车间内装甲装备小修作业活动,在考虑多条流水线并行作业及单道工序由多名维修工共同作业的条件下,提出一种基于维修网络流程更新的二进制矩阵编码的遗传算法。实验结果表明,通过迭代寻优计算,可以得到以维修工配置均衡度最高和维修总工期尽可能短为优化目标的维修人力资源配置最优方案,验证了算法的可行性,可以为部队装备维修人力资源配置方案的制定及优化提供理论与方法的支持。