基于测量误差的Fay-Herriot模型在小域估计中的应用研究
罗 薇,贺建风,谢贤芬
(1.广东工业大学 管理学院,广东 广州 510520;2.华南理工大学 经济与金融学院,广东 广州 510006;3.暨南大学 经济学院,广东 广州 510632)
一、引言
随着对多层次数据需求的日益增加,越来越多的调查数据不仅要提供总体目标变量的有效估计,还需要对总体的各级子域进行估计。一旦域样本量较小(通常称为小域),传统的抽样估计方法就很难直接得出有效的域估计量。于是,利用辅助信息建立小域与相关域(通常指与小域有关联的其他区域)的关联来增加有效样本量的间接估计方法成为小域估计研究的热点。从Rao、Longford、Datta等研究小域估计方法的经典文献来看,小域估计方法大体可分为基于设计的方法和基于模型的方法两类[1-3]。基于设计的方法,如广义回归估计和校准估计,只利用研究域内的信息来估计该域的目标变量。相比之下,充分利用域内以及其他相关域的信息,采用模型推断和条件推断相结合的基于模型的方法能够得出精度较高的估计量。依据所获得辅助信息的层次,基于模型的小域估计方法所使用的模型主要包括单元层次模型和区域层次模型两类。单元层次模型假定能够获取单元级别的观测数据和辅助信息[4],但这类辅助信息在现实中较难获得。如果缺乏单元层次的辅助信息,则使用小域层次汇总数据的区域层次模型[5]。区域层次模型使用较多的是Fay等提出的将直接估计和利用辅助变量建立模型所得的合成估计进行加权平均的一类随机效应模型。
Fay等提出的Fay-Herriot模型被视为小域估计模型推断方法应用的一个里程碑[6],Prasad等研究了Fay-Herriot模型参数估计问题[7],Diao等研究了Fay-Herriot模型的置信区间估计[8],于力超研究了多变量情形下的Fay-Herriot模型参数估计问题[9],李腾等研究了基于空间误差分量的Fay-Herriot模型在小域估计中的应用[10]。Fay-Herriot模型下目标估计量的偏差、均方误差的计算都依赖于辅助信息的完备性和准确性。目前关于Fay-Herriot模型的研究和使用上也大都假定了所有区域的辅助变量都可获得且不存在测量误差。然而,模型中的辅助信息通常来自于其他调查、行政记录和相关的普查资料等,亦可能存在抽样误差和非抽样误差,这些辅助变量作为Fay-Herriot估计量的协变量会给小域估计带来误差。Ybarra等将辅助变量的测量误差引入到Fay-Herriot模型中,发现忽略辅助变量的测量误差时,Fay-Herriot估计量的效果有时甚至比目标变量的直接估计更差,其均方误差也被低估[11]。
Fuller尝试将测量误差模型用于小域估计来解决上述问题[12]。小域样本中利用小域估计方法提升估计精度[13]。由于Fay-Herriot模型中的模型误差是随机的,他们直接假设回归模型的预测值加模型误差项就是带测量误差的协变量,但是这种处理仍然没有解决辅助变量本身存在测量误差的问题。另一些学者则考虑到辅助变量的测量误差,用辅助变量的估计值代替Fay-Herriot模型中辅助信息,这就需要对辅助变量的测量误差方差进行估计。为了解决测量误差方差估计问题,Ghosh等在结构型测量误差模型的假定下,引入嵌套误差模型,采用经验贝叶斯方法,利用矩估计得到模型参数的估计;作为对比,还采用分层贝叶斯方法,通过Gibbs抽样得到模型参数后验分布[14]。Ybarra等在函数型测量误差模型的假定下,假设辅助变量未知且非随机,但其估计值有固定的均值,并采用加权最小平均方法得到模型的回归参数和随机误差项的一致估计量[11]。Arima等则在随机型测量误差模型的假定下,假设辅助变量是随机的,其估计值均值等于辅助变量真值,并采用分层贝叶斯方法,利用矩估计得到模型参数联合后验分布,参数的边际后验分布具有有限方差[15]。Burgard等在Ybarra-Lohr模型的基础上,假设测量误差服从正态分布,利用极大似然方法和残差极大似然方法估计模型参数[16];并进一步将单变量模型扩展到测量误差二元Fay-Herriot模型[17]。Masoferi等在响应变量分布有偏的情形下,对响应变量采用区域层次对数测量误差模型,并对协变量采用对数测量误差模型,获得经验贝叶斯估计量及其均方预测误差[18]。上述方法仍存在着目标估计量依赖于误差模型参数假设的缺陷,或是存在计算测量误差方差困难、目标估计量均方误差不稳定等问题。
参考Ybarra-Lohr模型,在Fay-Herriot模型中引入测量误差,对多种数据来源进行整合的基础上进行小域估计,具体思路为:将直接估计量作为协变量对辅助估计量(因变量)进行回归,进而将直接估计量的抽样误差视为测量误差,解决测量误差方差估计难的问题。利用结构误差模型将直接估计量和辅助估计量关联起来后,Fay-Herriot模型转化为测量误差模型,可以用广义最小二乘估计法求出目标变量的最优线性无偏估计,以及对模型进行参数估计。相比于同类研究,本研究贡献在于:一是模型的适用性较好。模型引入了测量误差,却不需要限定测量误差类型,目标估计量不依赖于结构误差模型参数假设。二是模型的可扩展性强。模型适用于目标估计量和辅助信息来自于独立或非独立数据的情形,模型还容易拓展到有多个辅助信息来源的情形,且不会增加后续估计的难度。三是估计方法较简便。本文对小域目标估计量的估计方法较为简便,对模型参数的估计步骤也较为简单。四是估计方法的稳定性较好。一般来说,本文提出估计量的均方误差较小,也更为稳定。五是模型具有重要的现实意义和应用价值。在基于模型的小域估计方法研究中,模型中的辅助信息通常不可避免存在测量误差,利用带测量误差的辅助信息的小域估计模型来获得域层次变量的准确信息,将有利于小域估计方法的发展,应用在社会经济统计、农业统计的小域估计中。
二、传统的Fay-Herriot模型
Fay-Herriot模型的一般表达式为[6]:
(1)

(2)

Fay-Herriot估计的均方误差表示为:
(3)
(4)

三、基于测量误差的Fay-Herriot模型
Ybarra和Lohr在Fay-Herriot模型中引入测量误差后,在各参数已知的情况下,得出域i的总体均值一致估计为[11]:
(5)
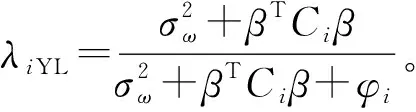
显然Ybarra-Lohr估计量的权数λiYL与辅助变量的测量误差有关,估计量的均方误差也受测量误差方差的影响。但是Ybarra-Lohr估计量仍存在一定的缺陷。与Prasad和Rao假设辅助信息不存在测量误差时相应的矩估计量相比[7],Ybarra-Lohr估计量下的模型误差方差估计量的方差较大,导致Ybarra-Lohr估计量的均方误差相对较高,且不稳定。
(一)模型改进

(6)
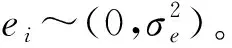

(7)
(8)
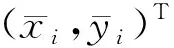
(9)

连接模型式(6)结合抽样模型式(8)以及线性混合模型得:
(10)

目前,将多层次模型整合到结构方程模型的框架中得到多层结构方程模型,是测量非抽样误差的主流方法。本文将Fay-Herriot连接模型式(6)和抽样误差模型式(9)相结合得到一个结构误差模型:
(11)
进一步转换为:
(12)

(13)

(14)
其中:

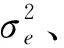
模型(11)还可以转换为:
(15)

(16)
及抽样模型:
(17)

(18)
目标变量的广义最小二乘估计为:
(19)

(二)模型参数估计
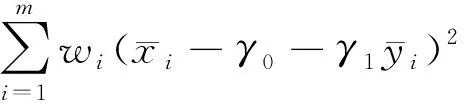
(20)
(21)
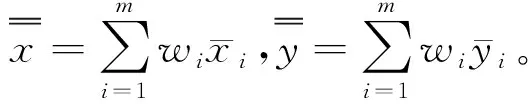
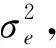
(22)
其中:
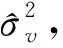
(三)均方误差估计

=M1i+M2i
(23)
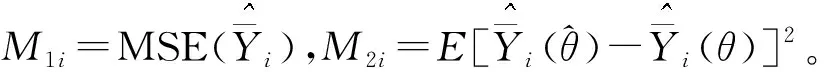
通过刀切法来求M1i和M2i的估计量,步骤如下:
第二步,计算M2i的估计量,由Jiang等的一般结论[25],
(24)
第三步,计算Mi1的估计量,当θ的参数已知时,结合式(14)得,
(25)

(26)
其中:
得到:
(27)
四、数值模拟和实例分析
(一)数值模拟
为了探究本文所提小域估计量的估计效果,本节设计了不同情形下的模拟实验,主要考虑全部小域辅助信息不存在测量误差、部分小域辅助信息存在测量误差和全部小域辅助信息存在测量误差三种情形,并对比本文所提估计量与其他常用小域估计量的效果。

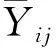
模拟1:全部小域的辅助信息不存在测量误差


表1 数值模拟结果比较
模拟2:部分小域的辅助信息存在测量误差


模拟3:全部小域的辅助信息存在测量误差
令k=100,V(bi)=3。此时,六种小域估计量的经验均方误差均值、刀切法估计的均方误差均值和均方误差方差与k=80,V(bi)=3时的情形类似。
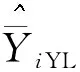
(二)实例分析
基于一个实际案例验证基于测量误差的Fay-Herriot模型下小域估计量的估计精度。Ybarra和Lohr采用2003—2004 US.National Health and Nutrition Examination Survey和2004 US.National Health Interview Survey进行实例分析发现,与小域的直接估计量相比,Ybarra-Lohr一致估计量的方差更小。本文则选取2015—2016 US.National Health and Nutrition Examination Survey(下文简称2015—2016 NHANES)和2016 US.National Health Interview Survey(下文简称2016 NHIS)的数据作为实例分析对象,研究辅助信息存在测量误差时几种小域估计方法的估计效果。
遵循Ybarra和Lohr的研究案例,将按照种族(墨西哥裔美国人、其他西班牙语系拉美裔、白人非西班牙语系拉美裔、黑人西班牙语系拉美裔和其他),年龄(20~29岁、30~39岁、40~49岁、50~59岁和60~84岁)以及性别(男、女)划分50个小域。2015—2016年NHANES对被调查者的医学检查包括了身高和体重,并计算出体重指数(下文简称BMI),BMI=weight/hight2。2016 NHIS也计算体重指数,不过其使用的体重与身高数据由被调查者自报,因此可能存在测量误差,用RBMI来表示NHIS体重指数。2015—2016 NHANES收集了9 544个被调查者的BMI数据,相应的小域样本量大小从20到360。2016 NHIS收集了33 028个被调查者的RBMI数据,相应的小域样本量大小从45到4 969。
由于2016年NHIS的RBMI数据与2015—2016年NHANES的BMI数据高度相关,我们用2016年NHIS的RBMI作为辅助信息,来改进2015—2016年NHANES的BMI小域估计量精度。利用上述调查数据,计算NHANES每个小域BMI均值的直接估计量、Fay-Herriot最优线性无偏估计量、Ybarra-Lohr一致估计量、广义最小二乘估计量及其均方误差。50个小域的四种小域估计量均方误差如图1所示,对四种小域估计量均方误差的分位数进行比较,如表2所示。显然,直接估计量的均方误差最大,Ybarra-Lohr一致估计量的均方误差较小,而广义最小二乘估计量的均方误差最小,与上文数据模拟的结论一致。在样本量较少的第16、21、33个域中,直接估计量、Fay-Herriot最优线性无偏估计量、Ybarra-Lohr一致估计量的均方误差较大,广义最小二乘估计量的均方误差相对较小,显示出较好的稳定性。

图1 50个小域BMI均值的四种小域估计量均方误差比较
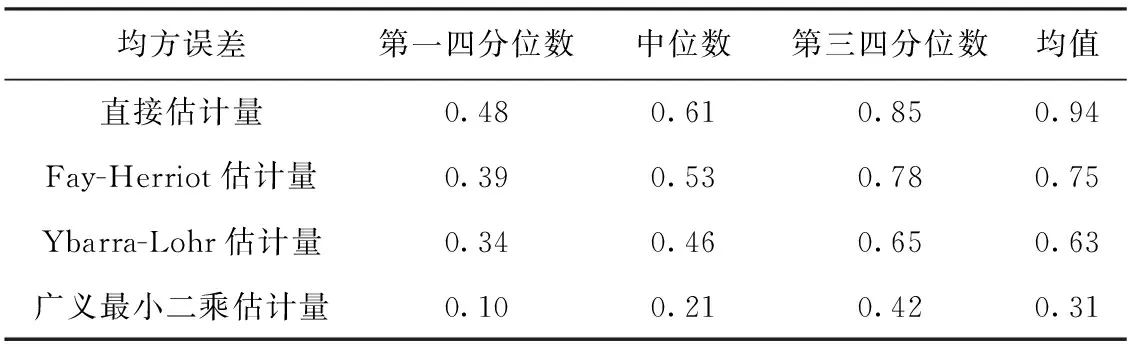
表2 50个小域BMI均值的四种小域估计量均方误差分位数比较
五、基于测量误差的Fay-Herriot模型在中国政府统计中的应用
随着社会经济对信息多层次、精细化需求的增加,以总体目标变量为估计目标的政府统计面临着新的挑战,即如何在得到有效的总体目标变量估计量的基础上,利用辅助信息,获得子群或小区域的目标变量估计量。小域估计是解决上述问题的有效方法,已经逐渐地应用于各种政府统计调查项目,如加拿大统计局在劳动力调查失业率和就业人数估计、健康特征估计及人口普查覆盖率不足估计中应用了小域估计方法;美国普查局在收入和贫困状况调查和现时人口调查中开展了小域估计项目。中国政府机构的管理层次分为国家级、省级、地市级、县级、乡级五级制,在社会经济管理中按上述层级实行分级管理和多层次决策。因此,中国政府统计应该相应地满足各级政府部门对各层次估计的需要。本章以中国的劳动力调查为例,阐述基于测量误差的Fay-Herriot模型在小域估计的应用思路和实施过程。
2005年11月,中国首次开展劳动力调查。2006年劳动力调查增加到一年两次,分别于5月和11月进行。从2007年起,劳动力调查每季度进行一次,分别于2月、5月、8月和11月进行。2009年,为更及时准确反映劳动力市场变化情况,中国组织实施大城市月度劳动力调查,当时的调查范围为全国4个直辖市和27个省会城市;从2013年4月开始扩大到65个城市。2016年1月,全国月度劳动力调查正式在全国范围内开展,调查范围覆盖全国所有地级市。中国劳动力调查的抽样目标是满足国家和分省(区、市)层面失业率等主要劳动力指标数据的要求,如果希望用估计总体的样本量去估计下级行政层级(如县、乡)的失业率、不同教育程度人群或各年龄段人群的失业状况,并达到一定的精度要求,其样本量往往就不够。因为按照现行的全国月度劳动力调查方案,仅在抽中的居(村)委会内,随机等距抽取连续4户组成的住户组,对抽中住户组内的所有人员进行调查,每个居(村)委会每月调查16户。在中国现行的住户类调查中,除了劳动力调查能够提供调查失业率的数据外,住户收支与生活状况调查也能够提供劳动从业情况的数据,不过由于住户收支与生活状况调查的主要调查目标是获取居民收入、消费及其他生活状况方面的信息,只简单地收集了调查户的从业人数和就业状况信息,可以认为由其提供的从业信息(失业信息)存在一定程度的测量误差。我们的目标是获得县层级失业率信息,假设劳动力调查没有测量误差,但是在县域中,失业率的直接估计量存在抽样误差。这样,我们就可以从劳动力调查和住户收支与生活状况调查分别获得失业率的直接估计量,通过结构误差模型来建立劳动力调查所得估计量和住户收支与生活状况调查所得估计量的关联,进而估计目标县域的失业率。

第一步,建立Fay-Herriot连接模型。当劳动力调查和住户收支与生活状况调查的失业率数据存在显著的线性相关时,以劳动力调查的失业率作为小域直接估计量,住户收支与生活状况调查的失业率数据作为辅助信息,利用Fay-Herriot连接模型式(6)来关联目标变量的直接估计量和辅助信息。考虑到中国的城乡二元经济结构,可以分城市和农村,分别建立两个Fay-Herriot连接模型。
第二步,建立抽样误差模型。由劳动力调查和住户收支与生活状况调查分别得到失业率的抽样误差模型,合并两个模型得到式(9)表示的抽样误差模型,对于第一步建立的两个Fay-Herriot连接模型,它们的抽样误差模型一致。
第三步,建立结构误差模型。将Fay-Herriot连接模型式(6)和抽样误差模型式(9)相结合,得到反映失业辅助信息和失业率关系的结构误差模型式(11)。

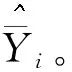
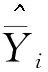
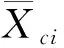
估计出模型参数和模型误差方差后,则可以计算其广义最小二乘估计量和相应的估计量均方误差。
在实践中,小域估计在农业统计和贫困率估计等领域也有着广泛的应用,借助于辅助信息对小域参数进行有效的估计。在实际数据收集时,一旦出现无法获得辅助信息精确数据的情况,即碰到测量误差数据的情形时,本文所提的小域估计方法可以有效利用辅助信息更稳健地估计域信息。
六、结论
Fay-Herriot模型是小域估计最常用的一类模型,其关键在于充分利用高质量的辅助信息建立目标小域与相关域之间的关联来提高小域估计量的精度。然而在现实中,无法保证辅助信息都是完整、正确的,即辅助信息可能存在测量误差。忽略模型中辅助变量的测量误差将影响目标变量估计的精度,低估其均方误差。因此,在Fay-Herriot模型中引入了测量误差,与抽样误差模型相结合后,构建了目标估计量和辅助信息的结构误差模型。该模型的广义最小二乘估计量是一个最优线性无偏估计量,具有Fay-Herriot估计量形式的同时,还能通过权数来调整测量误差对该估计量精度的影响。从模型形式看,结构误差模型容易将其他辅助信息纳入到模型中,方便通过多种数据来源的融合来提高小域估计的精度。由于该方法将直接估计量的抽样误差作为测量误差,通过结构误差模型来关联直接估计量和辅助估计量,所以无须对测量误差类型做出假定。相比已有的研究,本文方法的适用性更好,估计方法较为简便,估计效果也更为稳健。
数值模拟和实证分析结果表明,当辅助信息存在测量误差时,引入测量误差的Fay-Herriot模型效果较好。在没有测量误差的区域中,本文提出估计量的均方误差与同样引入测量误差的Ybarra-Lohr估计量的均方误差均值结果近似。在有测量误差的区域中,本文提出估计量比Ybarra-Lohr估计量均方误差均值要小。而且,从刀切法下的均方误差方差对比来看,Ybarra-Lohr估计量的均方误差方差变化较大,本文提出估计量的均方误差更为稳健。
为了模型设计和参数估计的简洁性,将模型和方法建立在以线性回归模型作为连接模型的基础上。为了提高模型估计量的精度、拓展模型的应用,还可以将线性回归模型拓展到广义线性回归模型,结合非线性测量误差模型来处理更复杂的情形。在大数据背景下,应用各类大数据作为辅助变量信息来提高小域估计的精度成为近年来一个活跃的研究方向,针对大数据公认的数据质量缺陷、高维缺失特点,后续研究可进一步探索大数据作为辅助变量的小域估计方法、参数估计方法,并进一步思考相关估计方法在统计调查中的具体应用。

