电加热鞋帮二维瞬态传热模型及其实验验证

刘广菊, 苏 云,2, 田 苗,2, 李 俊,2

(1.东华大学 服装与艺术设计学院, 上海 200051;2.东华大学 现代服装设计与技术教育部重点实验室, 上海 200051)

冬季恶劣的气候条件以及近年频发的极端气候对人体安全与健康提出了严峻挑战,足部作为人体远心端存在热平衡失调问题[1],易受到冷伤害,因此足部防寒在个体冷防护系统中至关重要。电加热技术的应用为足部防寒提供了有效途径[2-3]。然而,相关产品设计参数的设置依据不充分,使用者难免有过热或加热不足的体验。与此同时,人体实验往往存在成本高、极端环境实验安全性低以及个体差异性大的问题,且难以分析电加热鞋靴的传热机制,因此,亟需发展一种高效、适于极端冷环境的足-鞋传热模拟方法。

回顾以往的足-鞋数值传热研究,从最初评价鞋靴的隔热性能[4-5]开始,目前足、鞋的温度预测成为了最主要的研究,如Covill等[6]初步建立了足-鞋有限元模型以预测鞋内的温度分布。随着人体运动因素的引入,接触载荷下足-鞋界面的温度分布[7-8]愈受关注。然而,这些研究仅考虑了鞋帮、鞋底和空气的热特性,却很少考虑人体热调节过程,如人体血液流动和人体代谢产热对鞋靴热传递过程的影响。

基于足-鞋数值传热研究中的不足,以及足背-鞋帮的热损失大于足底-鞋底散热[6]这一现状,本文研究团队前期建立并验证了一维电加热鞋帮传热模型[9],模拟了织物多孔介质热传递、皮肤生物传热过程,预测了皮肤温度变化,一维模型的预测结果与实验结果吻合良好。然而,以往的织物模型对加热元件的热传递模拟研究不足,其中的发热体大都为均匀的热源[10]。事实上,加热片中的发热体并非全部覆盖基底,而是呈现排布形式,存在加热区与非加热区的差异。

为此,在一维电加热鞋帮数值模拟的基础上,本文通过有限体积法建立二维热传递模型,模拟发热体在加热片中的排布,分析模型的预测值与实验值之间的差异,探究二维模型与一维模型在电加热鞋帮传热问题中的科学性,为开发满足市场需求的电加热保暖鞋提供理论参考。

1 电加热鞋帮二维传热模型

电加热鞋帮的物理模型如图1所示。可以看到,自外环境至皮肤分别为织物层、加热片和皮肤层。对于4层织物系统,织物层包括外层、保暖层、内层和袜子;皮肤层则由表皮层、真皮层和皮下组织构成,血流灌注和代谢产热只发生在真皮层和皮下组织。

图1 电加热鞋帮的物理模型示意图Fig.1 Physical model of electrically heated upper of footwear

电加热鞋帮系统中,除质密的加热片以外,构成鞋帮部件的织物均视为多孔介质,数值模型的建立基于以下假设。

1)根据发热体的几何排布(见图2),结合加热片的温度分布特点,将加热片层的网格划分为加热区与非加热区。

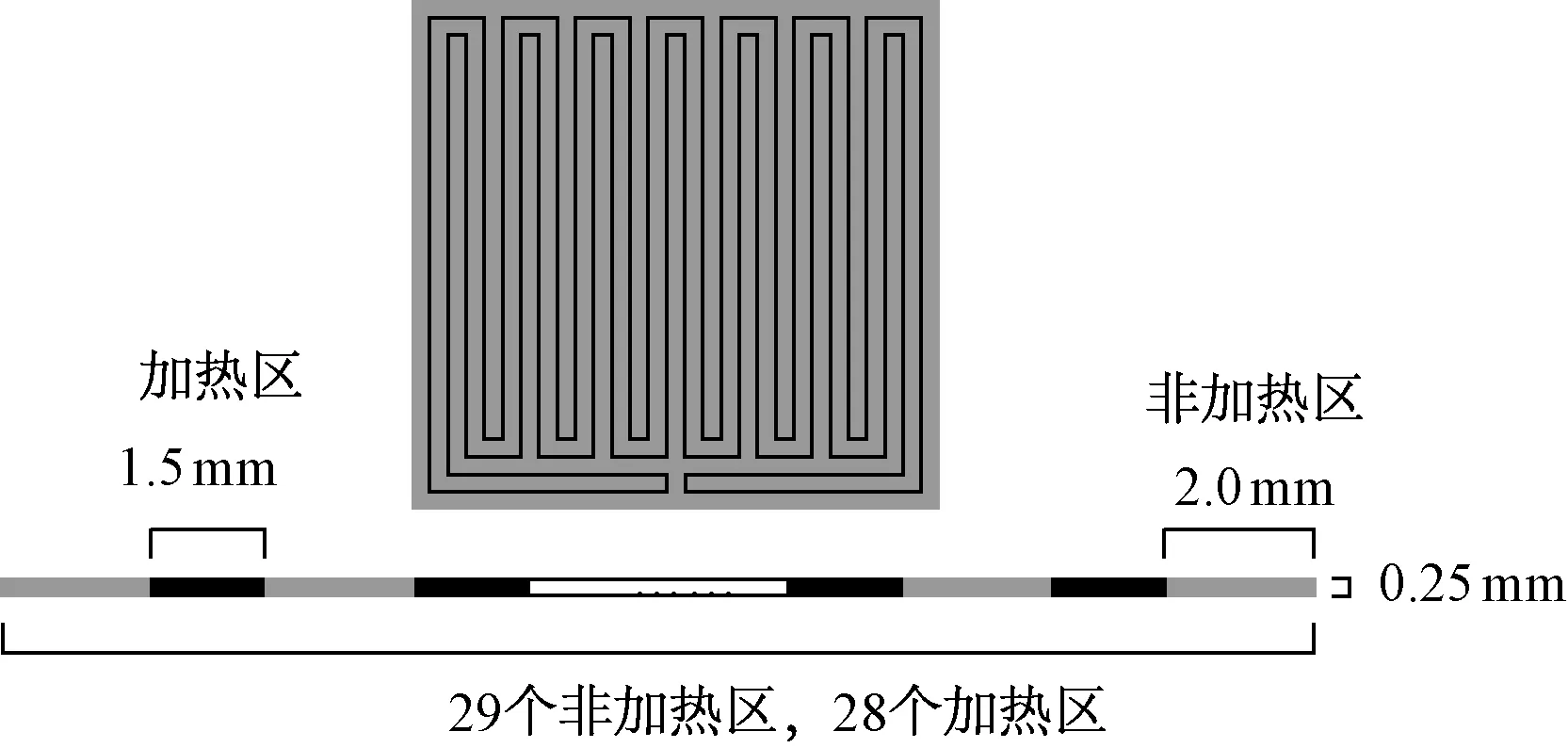
图2 加热片的几何特征示意图Fig.2 Geometric characteristics of heating pad

2)考虑鞋帮系统内部存在二维空间热传导,由于加热片在加热区和非加热区的平铺方向存在温度差异,因此假设二维传热沿厚度及其水平方向。

3)由于鞋靴内在的合脚性要求以及相对封闭的结构,不考虑鞋腔空间的热传递与鞋帮织物内部的辐射和对流传热,但考虑织物内空气对其导热系数的影响。

4)设定织物初始温度和皮肤舒适温度区间分别为22 ℃和34 ～ 36 ℃[11]。由于织物温度波动较小,因此将鞋帮织物的热物理性质参数视为常数[5,12]。

1.1 电加热鞋帮的传热控制方程

在二维控制体中,定义w、e分别为水平方向X的负方向、正方向,s、n分别为厚度方向Y的负方向、正方向,根据傅里叶定律,在时间、空间连续的温度场内,控制体P从0时刻到1时刻的瞬态宏观导热方程为

(1)

式中:x、y分别为X、Y的空间变量;T为温度,℃;ρ为物理层的密度,kg/m3;c为比热,J/(kg·℃);k为导热系数,W/(m·℃);等号右边的最后1项为加热源项;S为热源强度,W/m3。各物理层热传递的主要区别是其热物理性质参数和热源强度,因此下文将对二者进行说明。

1.1.1 鞋帮织物热传递模拟

为探究电加热系统的热传递与热调节机制,本文将一维模型中的鞋帮织物作为参数依据,具体信息如表1所示。由于织物无内热源,其热源强度为0,即式(1)中的S为 0。

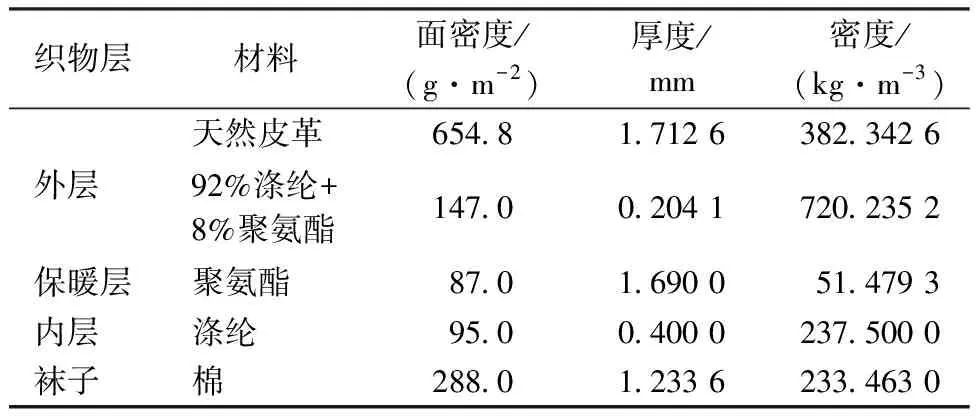
表1 鞋帮织物的基本性能Tab.1 Properties of upper of footwear

1.1.2 加热片热传递模拟

电加热元件的微型化以及柔性加热片的研发,为电加热元件置于鞋帮中提供了重要基础。本文选择目前发热性能较为稳定的合金加热片作为参数来源。合金加热片的发热体为铁铬铝合金材料,基底为聚酰亚胺材料,分别对应模型中加热片的加热区和非加热区。

当加热片不工作时,加热片的热源强度为0,其传热控制方程的形式与鞋帮织物一致;当加热片工作时,发热体的源项被激活,此时加热片中加热区的热源强度为功率系数k′与功率密度之积,即

S=k′P/V

(2)

式中:P为功率,W;V为发热体的体积,m3。

1.1.3 皮肤热传递模拟

由于血流灌注和代谢产热只存在于真皮层和皮下组织,因此表皮层的传热控制方程与织物层的形式一致。对于真皮层和皮下组织,其热源来自于血流灌注与代谢产热,故热源强度S为

(3)

1.2 模型求解

本文使用有限体积法对物理层的二维传热控制方程进行离散[16],具体步骤如下。

1)采用控制体的中心温度,令

(4)

2)采用温度的线性插值格式,设控制体P的右侧控制体为E,二者之间的距离为δxe,在控制体P与E之间,令

(5)

3)采用时间隐式格式,设控制体P的左侧控制体为W,二者之间的距离为δxw,在控制体P与W之间,令

(6)

通过以上近似替换,可将式(1)离散并进一步改写为系数方程形式,从而获得二维瞬态常系数矩阵,使用迭代法进行近似求解。

为使二维计算过程更快收敛,选择隐式线迭代方法,同时为平衡X、Y方向隐式线迭代的计算量,选择通用性较强的交替方向隐式线迭代[17]。根据物理层的规格尺寸,同时为使二维方向的网格呈现明显划分,规定X、Y方向的网格步长分别为5×10-4m和5×10-5m;时间步长为3 s,加热片的初始响应时间为18 s。由于实验测试中测量温度的精度为0.01 ℃,因此设定最大残差为0.001 ℃。

2 实验设计

模型验证实验中选用了防寒鞋材料中常用的双层(外层+袜子)和四层(外层+保暖层+内层+袜子)织物,以及市售典型合金加热片(100 mm×100 mm×0.25 mm),所用材料的基本性能[9,18]见表2。利用冷接触防护仪器[19],针对加热片的2类控温模式,即加热片控温模式(简称HPTC)和皮肤控温模式(简称STC)进行热传递实验,具体包括:加热片35 ℃ 控温、加热片45 ℃控温以及皮肤35 ℃控温,分别记为HPTC35、HPTC45和STC35。实验初始环境温度为22 ℃,初始皮肤温度为32.5 ℃,在冷板温度为-10 ℃ 的条件下进行时长为1 500 s的测试,从而得到不同控温模式下的皮肤温度与加热片温度。

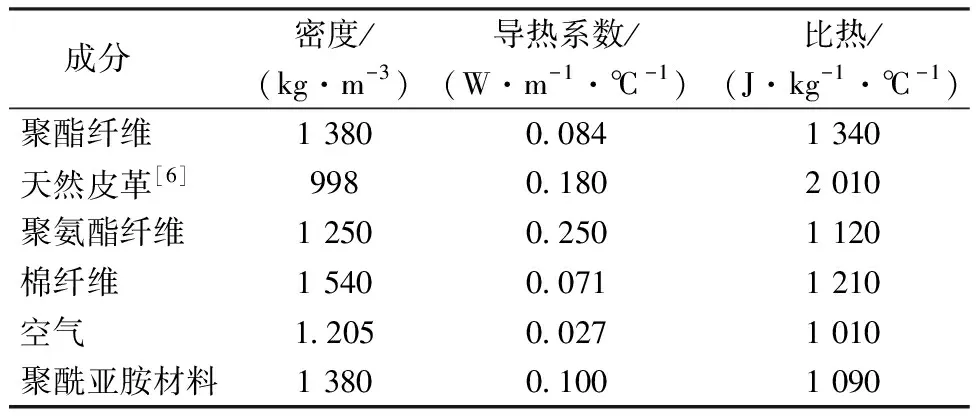
表2 材料与空气的基本性能Tab.2 Properties of materials and air

3 结果与讨论

3.1 皮肤温度

根据各实验组合的结果[9],皮肤温度的平均变异系数不超过1.5%,表明实验结果可靠。在发展二维模型的过程中,对一维模型同步更新了加热片参数、皮肤参数、网格参数以及迭代残差。

皮肤温度的一维、二维预测值以及实验值如图3所示。在加热片未响应阶段,实验测量的温度变化比模型慢,二维模型的散热相比一维更快。各实验组合中,二维模型的皮肤稳定温度(34.57～36.19 ℃)与一维模型基本一致,相差最大的情况为1.52 ℃(见图3(b))。以上现象源于热源模拟差异:二维模型下的加热片是由按一定间距、宽度排布而成的发热体所表征的,此时处于工作状态的加热区域并非一维模型中的整个加热片,因此,尽管一维和二维中热源强度一致,二维模型的初始皮肤升温较慢。

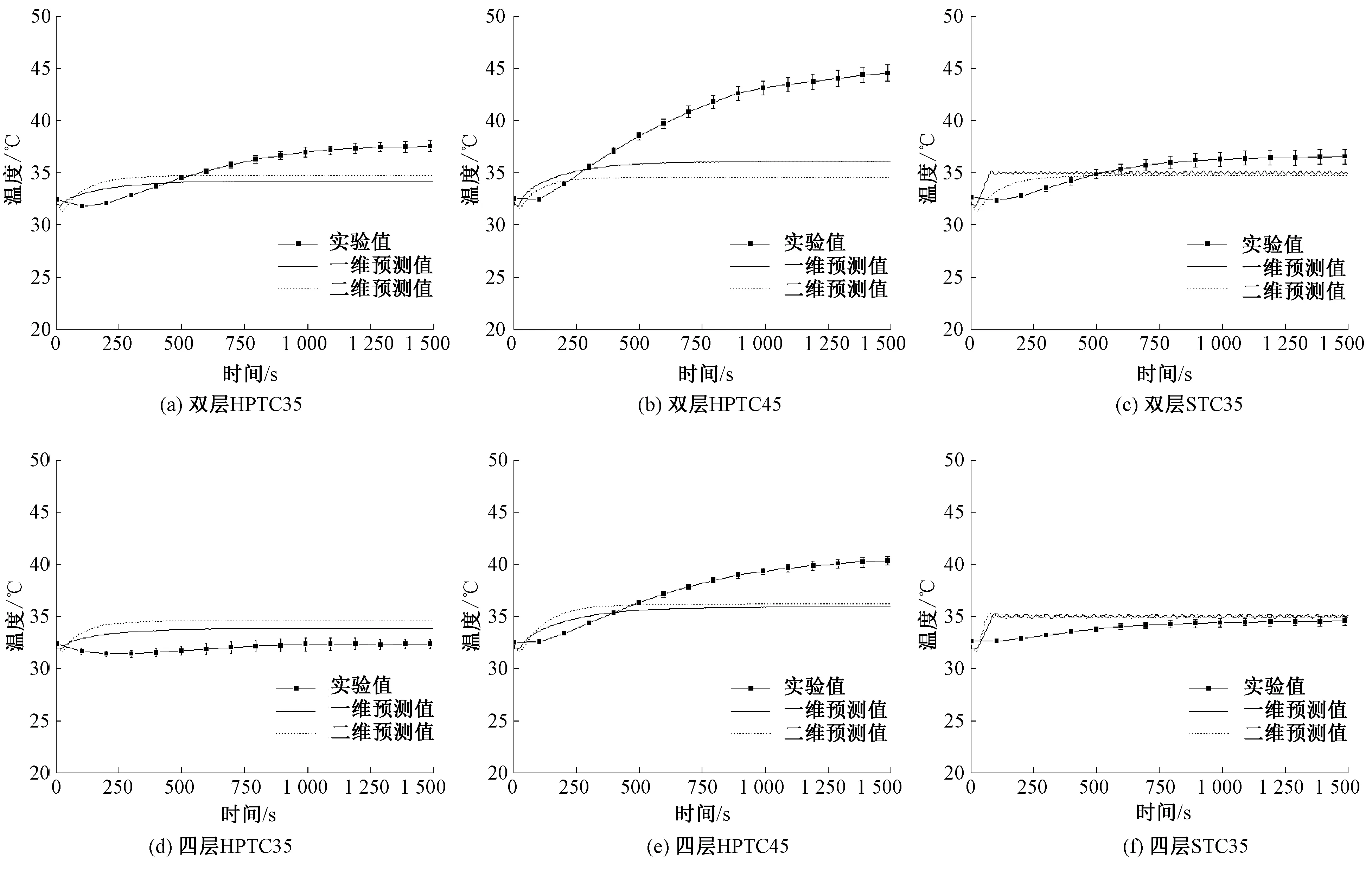
图3 数值模型与实验测试的皮肤温度变化Fig.3 Changes in skin temperature of numerical model and experiment.(a) HPTC35 mode of double-layer fabric; (b) HPTC45 mode of double-layer fabric; (c) STC35 mode of double-layer fabric; (d) HPTC35 mode of quadruple-layer fabric; (e) HPTC45 mode of quadruple-layer fabric; (f) STC35 of quadruple-layer fabric

一维、二维模型预测值与实验值的预测偏差如表3所示。首先对于二维模型的皮肤温度预测偏差(平均值为2.59%～13.74%),除双层织物在HPTC45模式下的平均值为13.74%外,其它情况下的均值皆小于7.50%。进一步地,2种模型的最大预测偏差均值皆出现在双层织物的HPTC45模式下,直观表现为图3(b)中实验值大于预测值,这主要受织物层的影响:一方面,双层织物的保暖性较差,没有四层织物中的保暖层,此时控温模式下的加热片需要更高的加热温度来达到设定温度;另一方面,加热片与皮肤之间的隔热较小,没有四层织物中的内层,皮肤温度也就更易受到高温加热片的影响。而模型中的皮肤内层边界温度恒定,对皮肤温度预测值进行了约束,因此模型预测结果小于实验值。另外,实验结果表明,当控温温度过高时,作为自由端的控温传感器具有更低的鲁棒性,因此加热片本身的集成化也是影响预测偏差的因素之一。

表3 一维、二维模型中皮肤温度的预测偏差Tab.3 Predicted deviations of skin temperature between one-dimensional model, two-dimensional model and experiment %

总体而言,在主要参数设定一致的前提下,一维和二维模型均能有效预测皮肤温度,且织物整体保暖性越好,一维和二维模拟结果的差距越小。具体而言,当织物的保暖性和加热片的设定温度相匹配时,HPTC模式下的二维模型优于一维模型,主要表现为一维、二维平均预测偏差的差值:-2.55%(双层HPTC45)<0.53%(双层HPTC35)。而在控温效果更佳的STC模式[9]下,二维预测精度高于一维,最大预测偏差降低了1.49%～3.93%。

3.2 加热片温度

图4示出加热片温度的实验值与一维、二维预测值的对比结果。根据实验中加热片的升温表现可将其温度变化主要分为初始升温阶段和温度波动阶段,其中在初始升温阶段往往出现峰值趋势。从模型预测结果可以发现,HPTC模式并未呈现明显的峰值趋势。这是因为此时的控温位置被设定在热源处,模型中的加热片响应及时。而当控温位置为皮肤表面时,热源首先需要延长加热时间将热量传递至皮肤,故出现了明显的峰值趋势。在温度波动阶段可以发现,二维模型的加热片温度仅在四层HPTC35、四层STC35呈现波动状态,这主要与模拟热源的性能有关。在实验中观察到,HPTC模式的加热片波动温度大于设定温度,这是由控温传感器的位置因素所致,二维模型能够体现位置分布,因此模型中已考虑这一现象,这就导致加热片被期望实现更高的控温温度,然而双层织物保暖性较差且加热片的热源受功率系数限制,因此加热片一直保持工作状态。

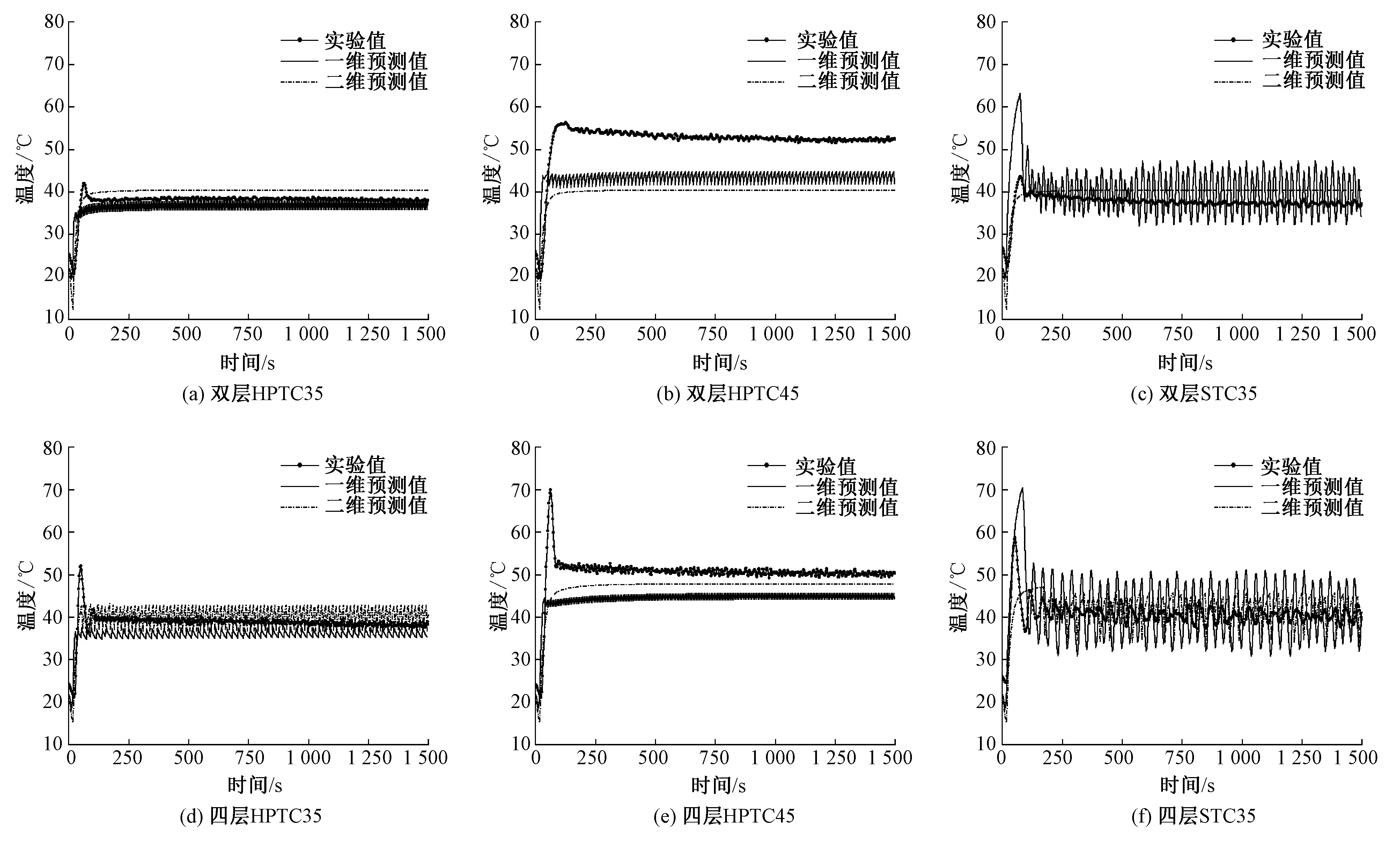
图4 数值模型与实验测试的加热片温度Fig.4 Changes in heating pad temperature of numerical model and experiment.(a) HPTC35 mode of double-layer fabric; (b) HPTC45 mode of double-layer fabric; (c) STC35 mode of double-layer fabric; (d) HPTC35 mode of quadruple-layer fabric; (e) HPTC45 mode of quadruple-layer fabric; (f) STC35 of quadruple-layer fabric

对于一维模型和二维模型,初始升温阶段的平均预测偏差、温度波动阶段的平均预测偏差如表4所示。其中:二维模型在初始升温阶段的预测偏差为11.28%～24.19%;在温度波动阶段,除双层织物在HPTC45模式下的预测偏差为23.55%,其余情况下的值均不大于7.06%。

表4 一维与二维模型中加热片温度的预测偏差Tab.4 Predicted deviations of heating pad temperature between one-dimensional model, two-dimensional model and experiment %

从表4看出,相比一维模型,二维模型降低了初始升温阶段的预测偏差,差值为2.99%～25.09%,其中对STC模式的预测精度提升最大。而在温度波动阶段,除四层织物在HPTC35、HPTC45模式下的预测偏差分别减小了3.36%、5.95%,其余情况均有所增加,增值基本在1.57%～2.45%之间,最大增值为双层织物在HPTC45模式下的情况,增加了5.89%,表现为图4(b)中二维预测值不仅低于实验值且低于一维预测值,这一现象依然源于二维模型中加热模拟的变化。

4 结 论

在一维电加热鞋帮模型的基础上,本文进一步提出了可模拟发热体排布特点的二维热传导模型,以改进电加热鞋帮热调节的预测效果。在电加热鞋帮的验证实验中,使用了2种隔热能力相差较大的织物组合,在模拟冷环境、模拟皮肤条件下得到了 2种控温模式的皮肤温度和加热片温度。通过一维、二维预测值与实验值的比较,得出以下结论。

1)电加热鞋帮的二维模型可模拟加热片的调温、传热过程并预测皮肤温度,鞋帮织物的保暖性越好,一维和二维预测值之间的差距越小。

2)一维和二维模型的皮肤温度预测值较为接近,皮肤稳定温度的差值不超过1.52 ℃。当鞋帮的防寒性与加热设定温度更为匹配时,如双层织物的HPTC35(加热片35 ℃控温)模式相比HPTC45(加热片45 ℃控温)模式,二维模型的皮肤温度预测能力比一维模型有所提高;尤其是在STC(皮肤控温)模式下,二维模型的皮肤温度最大预测偏差减小了1.49%～3.93%。

3)对于初始升温阶段的加热片温度,二维模型的预测偏差比一维减小了2.99%～25.09%;而对于温度波动阶段,加热片温度的预测偏差大都不超过7.06%。

4)相比一维模型,二维模型能够体现发热体与加热片的关系,在加热片的升温模拟方面更具优势。未来,通过进一步研究热源的功率系数并提高电加热服饰的集成化,二维模型将会更精准地预测电加热元件的调温表现。