基于惯量“削弱-补偿”责任分担的风电场虚拟惯量控制方法

李世春，王丽君，薛臻瑶，苏凌杰，王小雨，李振兴

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.梯级水电站运行与控制湖北省重点实验室（三峡大学），湖北宜昌 443002）

0 引言

在习近平总书记提出“碳达峰、碳中和”能源环境战略的指引下，构建大规模风电、光伏新能源主导的新型电力系统成为我国电网未来发展的主要方向。在此背景下，风电并网渗透率将会持续增加，将导致电网等效惯量不断削弱[1]、频率事故下的系统频率动态特性恶化[2]，电网面临的频率安全风险正日益增大[3]。

风电虚拟惯量控制方法从2003 年诞生以来[4]，被认为是解决上述问题的有效手段之一，其实现的基本原理为：当发生频率扰动时，通过触发附加惯量控制模块来改变风电机组电磁转矩和有功功率输出，从而抑制系统频率变化[5]。近年来，大量学者围绕如何更好地实现风电虚拟惯量响应的问题，研究了不同的虚拟惯量控制方法，主要有附加频率微分（Supplementary Frequency Differentiation，SFD）惯量控制[6-8]、基于功率跟踪优化的虚拟惯量控制[9]、转差率反馈惯量控制[10]、基于储能-风电协调的惯量控制[11]、基于功率跌落和机械载荷优化的虚拟惯量控制[12]等典型方法，研究者主要从如何优化风电机组惯量响应功率跟踪过程、提高惯量响应强度、优化惯量响应结束后功率跌落程度和机械载荷冲击问题等方面切入提出改进策略，以上5 种方法主要从机组自身控制角度推广到系统频率影响[13]，缺乏从风电并网责任及应提供的惯量支持要求来研究针对性的控制方法。

事实上，是否实施虚拟惯量控制[14]对于风电场具有“对自身不利”与“存在责任”的双重博弈性。一方面，技术实施会对风电场产生几方面不利影响：（1）风机偏离最佳转速和最大功率跟踪状态，降低发电经济性[15]；（2）所提供的惯量支持越大、动能释放越多，会伴随更长的转速恢复及扰动过程[16]；（3）风机转子转速频繁变化，引起轴系扭矩作用力，缩短机组寿命[17-18]。风电场提供的惯量支撑强度越大、持续过程越长，这些不利影响就越突出。在另一方面，风电场并网引起电网等效惯量不断削弱，应该通过实施虚拟惯量控制来承担补偿电网惯量的责任。因此，科学认定惯量削弱责任与相匹配惯量支撑强度的控制方法将有助于在风电场推广应用。

本文研究基于惯量“削弱-补偿”责任分担的风电场虚拟惯量控制方法。首先提出基于惯量“削弱-补偿”分担的思想计算风电场/风电机组虚拟惯量补偿目标，再重点求解惯量补偿目标与惯量控制参数的时域函数关系，最后通过动态调整关键控制参数来执行具体控制策略。

1 基于“削弱-补偿”分担思想的风电场惯量补偿目标计算

当不考虑风电、光伏等新能源接入时，电力系统等效惯量可表示为[19]：

式中：n为系统电源数；Sg,j，Hg,j分别为第j个电源的额定容量和惯量；xj为第j个电源的开停机状态（1 为开机，0 为关机）；S(0)Σ为系统中开机状态下电源的额定容量之和。

式（1）可表示日内不同时段的系统惯量H(0)，随着系统运行方式变化，可通过调度信息（包括机组xj，Sg，j，Hg，）j计算各时段的惯量值。在式（1）中，系统已开机的电源均能提供旋转惯量，能够共同支持系统频率稳定。

当风电并网时，电力系统等效惯量H(1)为：

式中：Sw,Σ，Hw,Σ分别为并网风电的额定容量和惯量；yw∈[0，1]，为风电总体开机状态，当存在部分风机停机时，yw＜1。

由于风电在常规控制下惯量为0，即式（2）中Hw,Σ=0，风电并网会使系统等效惯量降低，即H(1)＜H(0)，随着风电并网容量增加，二者差距越大。因此，无惯量贡献的风电并网，挤占了同步机组的容量占比，导致电网惯量削弱，这是大规模风电并网导致系统惯量显著削弱、频率动态特性恶化的根本原因。为避免上述问题。从公平分担并网责任的角度，风电并网前后应维持系统惯量保持不变，即满足：

当系统包含m个风电场时，式（3）可展开为：

式（3）与式（4）中：y1…yi…ym分别为风电场1…i…m开停机系数，yi为开机额定容量与风电场i额定容量的比值，且yi∈[0，1]；分别为全网风电总体、风电场1…i…m可提供的惯量补偿量；Swf，1…Swf，i…Swf，m为各风电场额定容量。

对于式（4），H(0)，S(0)∑，Swf，1…Swf，i…Swf，m，y1…yi…ym为已知量，易于获得，而存在无数组解。其中，有1 组特殊解为：

按该解集在各风电场补偿惯量时，能体现“按容量分担惯量削弱责任”的公平性。一方面，当时，式（4）中任一风电场i提供的动能为反映出各风电场提供的动能与并网额定容量呈正比。另一方面，式（5）解集的物理意义还在于：对任意本身不具备惯量的并网电源，例如光伏，都可以按照与系统原有惯量H（0）相等的原则补偿模拟惯量，按并网额定容量承担频率控制责任，具有良好的推广性。因此，本文将以式（5）分配风电场惯量补偿目标，再依据目标值确定具体控制策略。

2 风电场虚拟惯量补偿控制方法

基于电网惯量“削弱-分担”的思想，求解风电场的惯量补偿量，进一步将风电场惯量补偿目标分配到风电机组，执行各机组的虚拟惯量补偿控制策略。首先将式（5）中风电场惯量补偿量转换为风电机组惯量补偿目标，再建立惯量补偿目标与控制参数的时域函数关系，通过调节控制参数来跟踪响应补偿目标。

2.1 风电机组惯量补偿目标

对于系统中任一风电场i，假设场内包含L台风电机组，则根据式（5）确定的H′wf，i可表示为：

式中：zil为风电场i第l台风电机组的开停机状态（1 为开机，0 为关机）分别为风电场i第l台风电机组的额定容量和惯量补偿目标。

基于式（5）的分配思想，为体现风电场内按额定容量分担惯量削弱责任的原理，各风电机组也应满足：

2.2 惯量补偿目标与控制参数的时域函数关系

现有虚拟惯量控制方法均是通过设计不同的控制策略、参数等模拟出风机和风电场惯量。而本文是根据惯量补偿目标，反过来确定具体控制任务，属于新的问题，但需要基于某种惯量控制策略来执行。考虑SFD 惯量控制策略[6-8]是经典的风机虚拟惯量控制方法，本文基于该方法建立惯量补偿目标量与控制参数之间的函数关系。

根据文献[10]可知，双馈风电机组相对于系统同步角频率变化的虚拟转动惯量Jequ可表示为：

式中：JDFIG，ωr0，Δωr分别为双馈风电机组固有转动惯量、转子初始角频率和转子角频率增量；ωs0，Δωs分别为系统初始同步角频率和角频率增量。

根据式（8）和惯量的基本定义[20-21]，双馈风电机组等效虚拟惯量Hequ可表示为：

结合式（9）和文献[19]，可得Hequ的复频域表达式为：

式中：s为复参变量，称复频率；Kdf，Tf分别为虚拟惯量控制增益和滤波时间常数；KpT，KiT分别为速度控制器的比例系数和积分系数。

将式（10）整理为：

其中，

式中：α1，α2，α3为式（12）分母的三个单根；K1，K2，K3为式（12）部分分式的展开系数。

然而，对于不同的风机型号，KpT，KiT等参数存在差异，需要根据实际参数确定Hequ(t)属于式（13）—式（14）中哪种情况。

式（13）—式（14）为对应Kdf，ωs0，ωr0及相关物理/控制参数（HDFIG，ωnom，KpT，KiT，Tf）的双馈风电机组等效虚拟惯量时域值。根据式（13）和式（14），在影响Hequ(t)的众多参数中，HDFIG，ωnom，KpT，KiT，Tf为恒定值，ωs0在稳态时为额定值，Kdf和ωr0共同决定Hequ(t)。

因此，若要补偿风电场并网而削弱的电网惯量，模拟出式（7）对应的风电机组虚拟惯量利用式（13）—式（14）的Hequ(t)-Kdf、ωr0时域函数关系，根据风机惯量补偿目标H′wt,il反过来确定控制增益Kdf,il：

各台风机根据实时风速及对应角频率ωr0,il，通过设置式（15）的控制增益Kdf,il执行虚拟惯量补偿控制策略，即可响应惯量补偿目标，整个风电场即可响应补偿的虚拟惯量H′wf,i，最终所有风电场并网引起的电网惯量削弱得以补偿。

2.3 控制策略执行

2.2 节建立了风电机组虚拟惯量补偿目标与控制参数之间的函数关系，下面陈述风电机组虚拟惯量补偿控制策略的具体执行方案。

2.3.1 控制增益Kdf,il的动态设置方法

在式（15）中，关于Kdf,il的表达式是复杂的，并且需要根据判别式Δ和不同风速下的转子角频率ωr0,il来确定与的具体函数关系。为了直观地反映上述因素对Kdf,il取值的影响，图1 和图2 分别绘制了给定时不同判别式Δ值和风速下的Kdf,il曲线。

图1 不同风速下的Kdf,il 曲线（对应式（15）、Δ＜0）Fig.1 Kdf,il curves under different wind speeds（corresponding to equation（15），Δ＜0）

图2 不同风速下的Kdf,il 曲线（对应式（15）、Δ≥0）Fig.2 Kdf,il curves under different wind speeds（corresponding to equation（15），Δ≥0）

由图1 和图2 曲线可知，在t1时刻附近以及时间t趋近无穷时均出现了Kdf,il取极值情况，下面以风速为10 m/s 工况时对图1 出现极值现象进行说明。

首先，可将式（14）转化为以下形式：

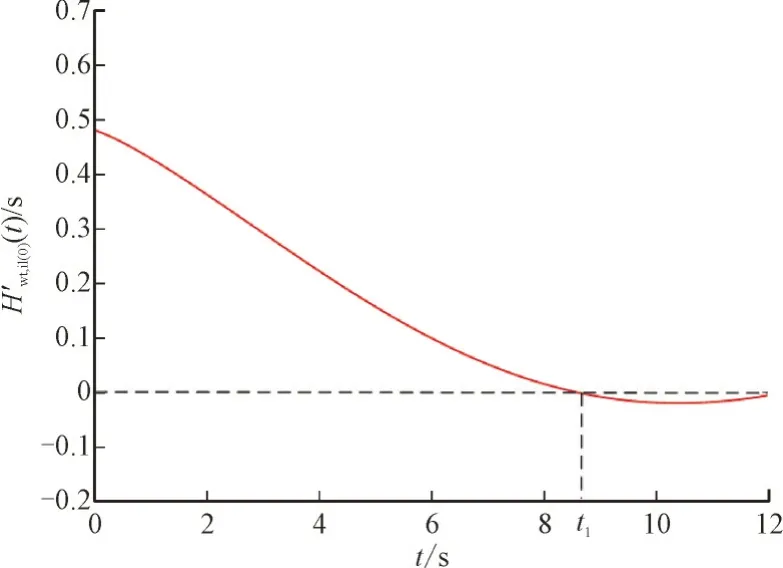
图3 风速=10 m/s下的曲线（Δ＜0）Fig.3 curve at wind speed of 10 m/s（Δ＜0）

在图3 中，t1时刻之后出现，这是由于风机转子角频率变化Δωr与系统角频率变化Δωs不同步，使Δωr和Δωs同时出现正、负值，根据式（9）可知，这会使Kdf,il出现负值。

综上分析结果，若直接根据式（15）对应的2 种情况（图1 和图2）设置Kdf,il，存在2 个问题：（1）Kdf,il设置过大会导致功率自激振荡，使控制系统失去稳定性[22]，因此Kdf,il为无穷大时应进行限制；（2）Kdf,il曲线连续时变，如果据此设置参数、频繁改变Kdf,il，会出现电磁转矩振荡、输出有功功率不稳定现象。为解决这2 个问题，可采取如下的Kdf,il动态设置方法：

1）在惯性响应动态过程中，Kdf,il每0.1 s 周期改变一次，每个设置值为周期内Kdf,il曲线的积分均值Kdf(av),il(t)为：

式中：积分下限u=[10×t]/10；积分上限w=（[10×t]/10）+0.1；符号[*]表示取整运算。

2）若Kdf,il在t1（-），t1（+）时刻趋于∞时，令该时刻所在周期的Kdf,il设置值为前1 个周期Kdf,il积分均值。

3）当连续检测到经Butterworth 低通滤波器（剔除高频噪声）滤波后[23]的系统频率变化率RoCoF≤ε（设定的精度误差）时，表明频率响应趋于稳态，设置Kdf,il=0，惯性响应截止。

2.3.2 控制策略执行的全流程

基于上述理论过程，整理所提出的风电场虚拟惯量补偿控制策略实施流程如图4 所示，并可按如下步骤执行：

图4 风电场虚拟惯量补偿控制策略执行流程图Fig.4 Implementation flow chart of virtual inertia compensation control strategy for wind farms

2）计算风电机组实时控制增益Kdf,il。将步骤1）中得到的风电场惯量补偿目标，代入式（7）求取各风电机组惯量补偿目标，再利用式（15）计算各风电机组实时控制增益Kdf,il。

3）动态设置控制增益Kdf,il。根据逻辑条件判断频率扰动大事故发生时，对Kdf(av),il(t)进行快速动态设置，执行虚拟惯量补偿控制策略；若频率事故未发生，设置Kdf,il=0。

3 算例验证

为验证本文所提控制方法和策略的有效性，利用Matlab/simulink 对如图5 算例系统进行验证。在该算例中接入了W1 和W2 2 个风电场。算例系统运行时涉及4 种风况，用于模拟实际运行中风电场和机组的不同风速状态。风况1 的风速为8 m/s；风况2 的风速为9 m/s；风况3 的风速为10 m/s；风况4的风速为11 m/s。

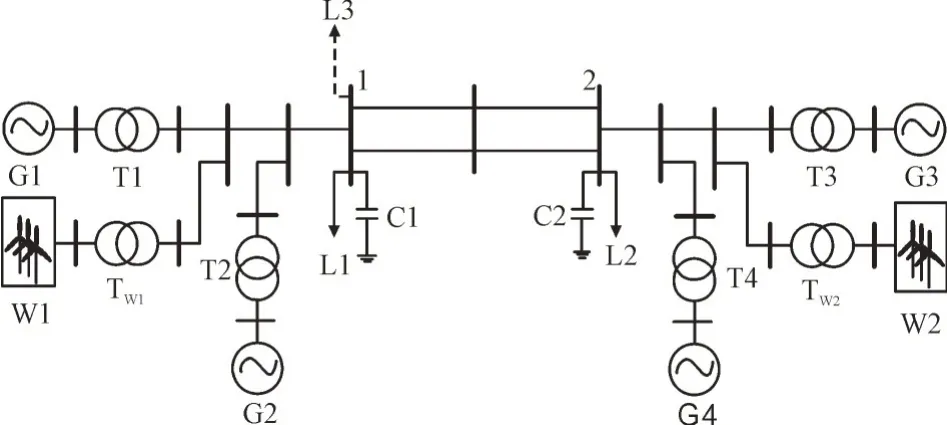
图5 算例系统Fig.5 Test system

图5 中，G 为发电机，Tw为变压器，L 为负荷，C 为电容。

3.1 风电场虚拟惯量补偿控制策略对电网惯量补偿效果验证

风电场W1 和W2 均处于风况3 下，设置t=100 s时，突增负荷L3=160 MW（占总负荷10%），模拟系统发生频率事故，按照图4 控制流程动态设置控制增益Kdf，il，执行风机虚拟惯量补偿控制策略。分别提取风电场离网、风电场虚拟惯量补偿控制、风电场并网无控制3 种情况下的系统频率响应曲线进行对比。

如图6 所示，（1）风电场并网（无控制）与离网状态相比，频率跌落速度要快得多、频率跌落最低点明显更深，频率动态特性显著恶化，而这正是由于电网惯量削弱引起；（2）风电场并网时，通过实施虚拟惯量补偿控制策略，可使其频率响应动态特性与离网时接近（频率跌落速度与频率最低点都较接近），频率动态特性维持较好。

图6 风电场虚拟惯量补偿控制影响的频率响应曲线Fig.6 Frequency response curves affected by virtual inertia compensation control of wind farms

系统频率变化率是反映频率动态特性的关键指标，也是决定频率跌落最低点的关键因素，可用最大频率变化率为-ΔPLf0（/2HeqS∑）（ΔPL为功率缺额，f0为系统初始频率，Heq为系统等效惯量，S∑为系统容量）来定量描述[24]。因此，为了更直观表现本文虚拟惯量补偿控制的准确性和效果，提取了对应图6 中3 种条件下、频率扰动发生后0.5 s 内的频率变化率曲线。

如图7 所示，在频率扰动发生后的0.5 s 内（该时段对频率跌落最低点影响最显著），在风电场并网（无控制）条件下RoCoF 明显更大，而通过虚拟惯量补偿控制可使其RoCoF 与风电场离网条件下接近，说明控制方法能准确地补偿电网惯量削弱，这也促使图6 中二者的频率动态响应过程较一致。

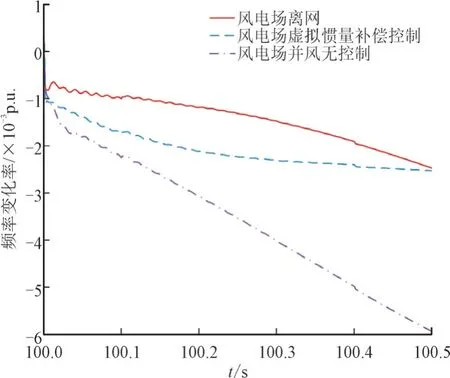
图7 风电场虚拟惯量补偿控制影响的RoCoF曲线Fig.7 RoCoF curves affected by virtual inertia compensation control of wind farms

3.2 不同风速下控制策略的效果验证

由式（15）可知，需要根据风电场实时风速（决定ωr0，i）l动态调节控制增益Kdf，il，才能准确补偿风电场并网引起的电网惯量削弱。鉴于此，为反映风电场、风电机组不同风速及控制的差异性，将2 个风电场中的风电机组各分为3 组：风电场W1 的3 组风机分别为风况1—风况3，风电场W2 的3 组风机为风况2—风况4；然后执行风电场惯量补偿控制策略，分别得到频率响应特性曲线、频率变化率曲线和风电场W1 中3 组不同风速的风电机组惯量补偿情况如图8、图9 和图10 所示。

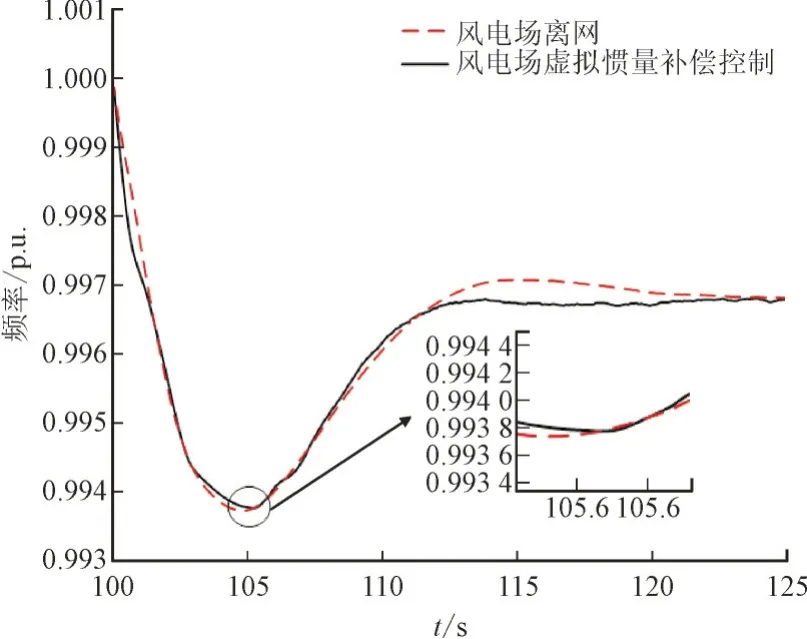
图8 不同风速下控制影响的频率响应曲线Fig.8 Frequency response curves affected by different control of wind speeds

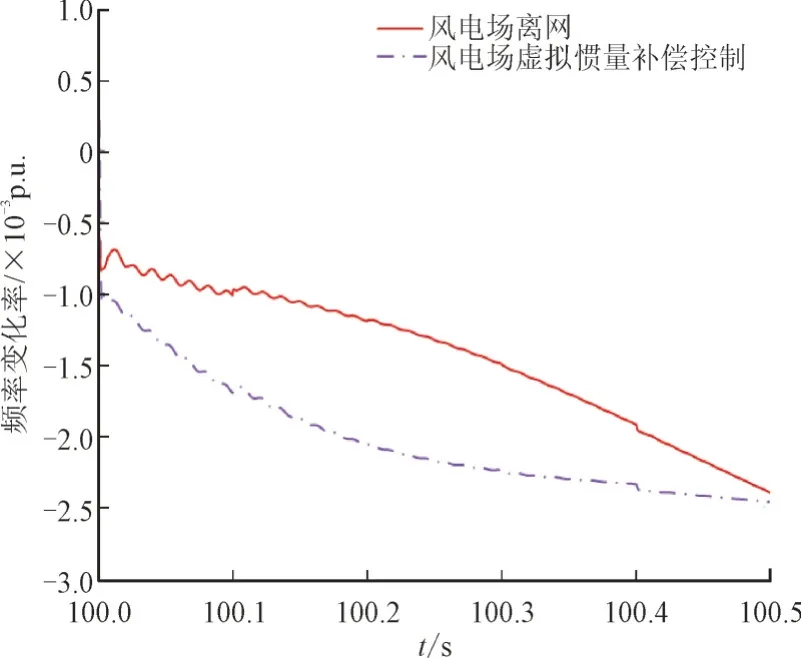
图9 不同风速下控制影响的RoCoF曲线Fig.9 RoCoF curves affected by different control of wind speeds

图10 风电场W1 3组风电机组惯量补偿跟踪曲线Fig.10 Three groups of inertia compensation tracking curves for wind turbines in wind farm W1

由图8—图10 可知：（1）在该状态下，通过风电机组虚拟惯量补偿控制的频率动态响应曲线、RoCoF 曲线均与离网状态时很接近，说明即使不同区域的风电场风速不同、同一风电场内风机切入风速存在差异，仍能通过动态调整控制增益Kdf，il去适应；（2）在不同风速下，风电场W1 中3 组风电机组补偿惯量响应值与惯量补偿目标（6.28 s）非常吻合，最大惯量偏差控制在2%以内，说明本文方法能适应风速变化下的惯量精确跟踪补偿。

3.3 不同风电渗透率下控制策略的效果验证

为验证不同风电渗率下惯量补偿控制策略的效果，在3.2 节所述不同风速的基础上，设置风电渗透率（pene.）分别为10%，25%和50%，频率事故发生时的频率响应特性曲线和频率变化率曲线如图11 和图12 所示。

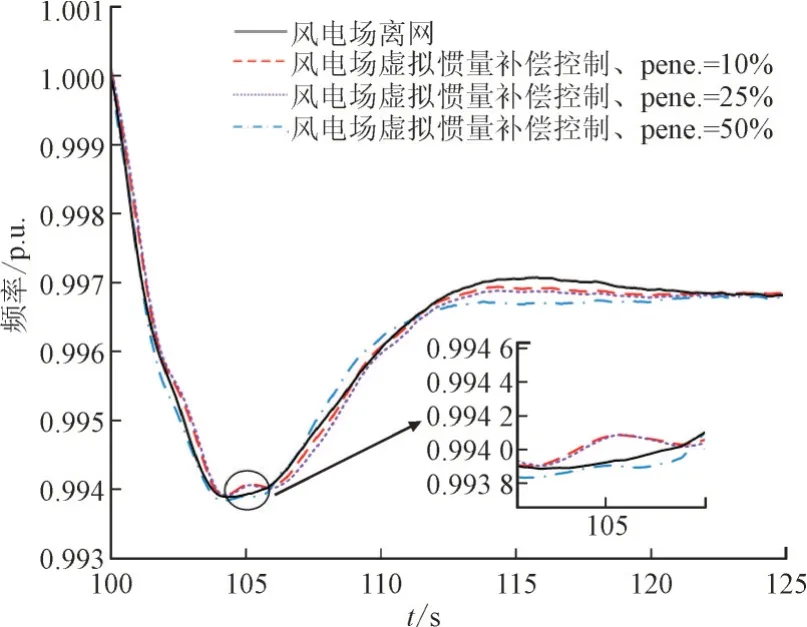
图11 不同风电渗透率下控制影响的频率响应曲线Fig.11 Frequency response curves affected by different control of wind power penetrations

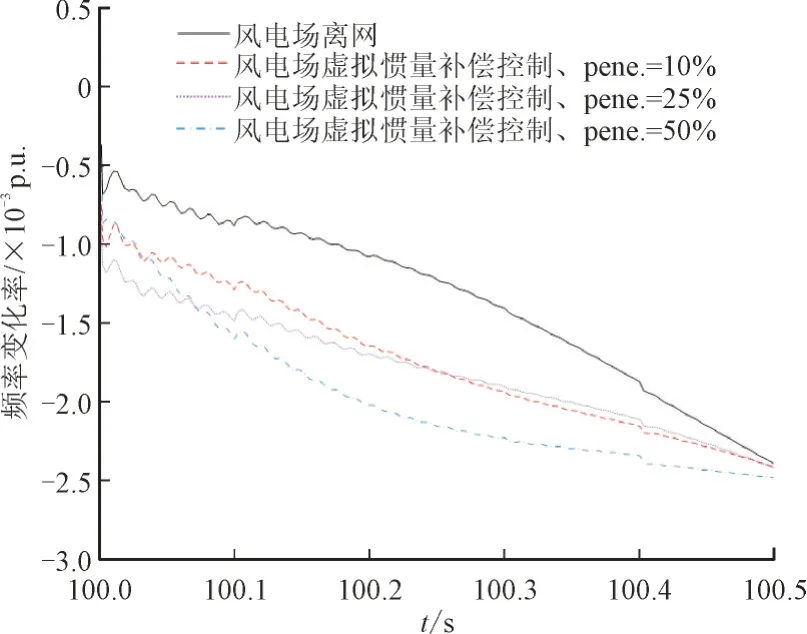
图12 不同风电渗透率下控制影响的RoCoF曲线Fig.12 RoCoF curves affected by different control of wind power penetrations

对比图11 和图12 可知：（1）不同风电渗透率水平下，通过实施风电机组虚拟惯量补偿控制策略，对应的频率动态响应曲线、RoCoF 曲线均与离网状态时较接近，均能较准确补偿电网惯量，控制效果良好；（2）随着风电并网渗透率增大，仍能应用本文所提方法来保障电网惯量水平、有效避免系统动态频率特性恶化。

4 结论

本文基于惯量“削弱-补偿”责任分担的思想，研究了风电场虚拟惯量控制方法，通过理论分析与算例验证得出如下结论：

1）风电场按照与系统原有惯量相等的原则补偿模拟惯量，提供的动能支持与其并网额定容量呈正比，体现了根据“削弱-补偿”分担并网责任的公平性。

2）风电场并网导致系统动态频率特性显著恶化，通过执行风电场虚拟惯量补偿控制策略，可使系统频率响应曲线与并网前情况接近，系统动态频率特性维持良好。

3）风电场虚拟惯量补偿控制策略可根据风速变化动态调整控制增益，准确补偿风电并网对电网惯量的削弱，保证频率事故下的频率支撑能力，控制策略具有良好适应性。

4）随着风电渗透率增大，仍能应用本文控制方法来保障电网惯量水平，有效避免系统动态频率特性恶化。