考虑渗流作用和围岩损伤的地铁隧道下穿古运河区段变形分析

李 杨 吴旭平 徐立明 杨新安

(1.云南省发展和改革委员会,650051,昆明; 2.浙江省交通投资集团有限公司,310016,杭州;3.浙江杭温铁路有限公司,311202,杭州; 4.同济大学交通运输工程学院,201804,上海∥第一作者,经济师)

青岛地铁13号线香江路站至井冈山路站(以下简称“香井区间”)需要下穿马濠运河。该运河开凿于元、明两代,历史悠久,属当地的市级重点文物保护单位。香井区间隧道的埋深较浅,距马濠运河的最小垂直距离仅为14.89 m,施工难度较大。香井区间所处地层为富水松散地层,具有含水量大、渗透性强、强度低、松散程度高等特点。

香井区间施工过程中,地下水渗流量较大,富水松散地层的渗流-应力耦合作用难以忽略。本文基于渗流-应力耦合理论展开的隧道稳定性的研究成果[1-5],对富水松散地层非饱和渗流特性进行试验,同时考虑围岩损伤后的强度变化情况,采用FLAC3D软件开发相应的渗流-应力耦合计算模块,以探究地铁隧道开挖对马濠运河的变形影响。

1 工程概况

马濠运河位于香井区间隧道东侧[6]。该运河暗渠由20 cm厚钢筋混凝土盖板、36 cm厚钢筋混凝土底板、50 cm厚小块石垫层及浆砌片石侧墙组成。马濠运河暗渠与地铁13号线隧道左线、右线的关系如图1所示。表1为马濠运河地层及运河材质的主要物理力学参数。

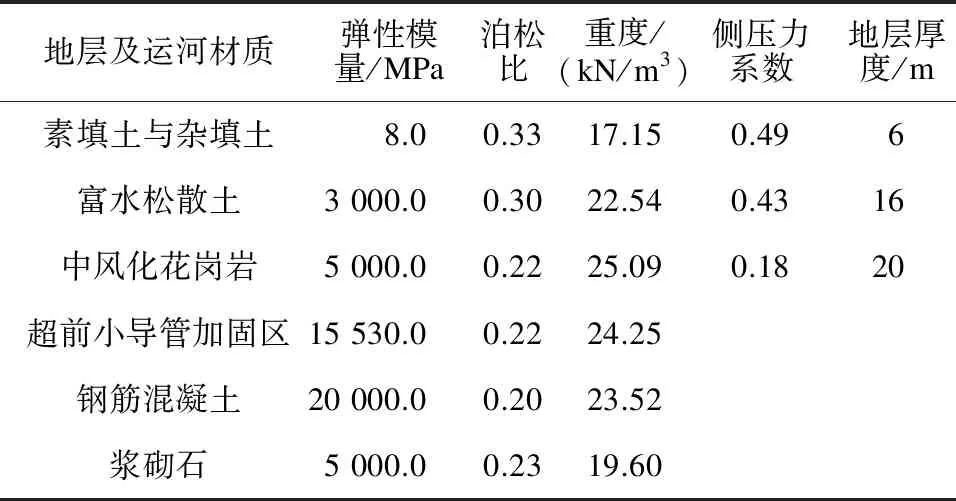
表1 马濠运河地层及运河材质的主要物理力学参数

图1 马濠运河暗渠与地铁13号线隧道左线、右线的关系

2 地层的非饱和渗流特性

香井区间穿越的地层为富水松散地层,该地层具有含水量较大、松散程度较高的特性。针对含水量较高的特点,需考虑该地层中的地下水渗流作用。针对松散程度高的特点,需考虑松散土体的粒径特征及地层持水能力对地下水渗流的影响。

2.1 初始含水率、土体粒径对渗流系数的影响

为探究不同粒径下土体的渗流系数变化情况,本文采用试验筛对香井区间场区内的土样进行筛分,分别选用了0.075 mm、0.250 mm、0.500 mm、1.000 mm等4种不同的筛分孔径,除1.000 mm孔径的筛分土样采用常水头渗流装置进行测量外,其余孔径筛分土样均采用变水头渗流装置进行测量。不同粒径下土体渗流系数与初始含水率的关系如图2所示。

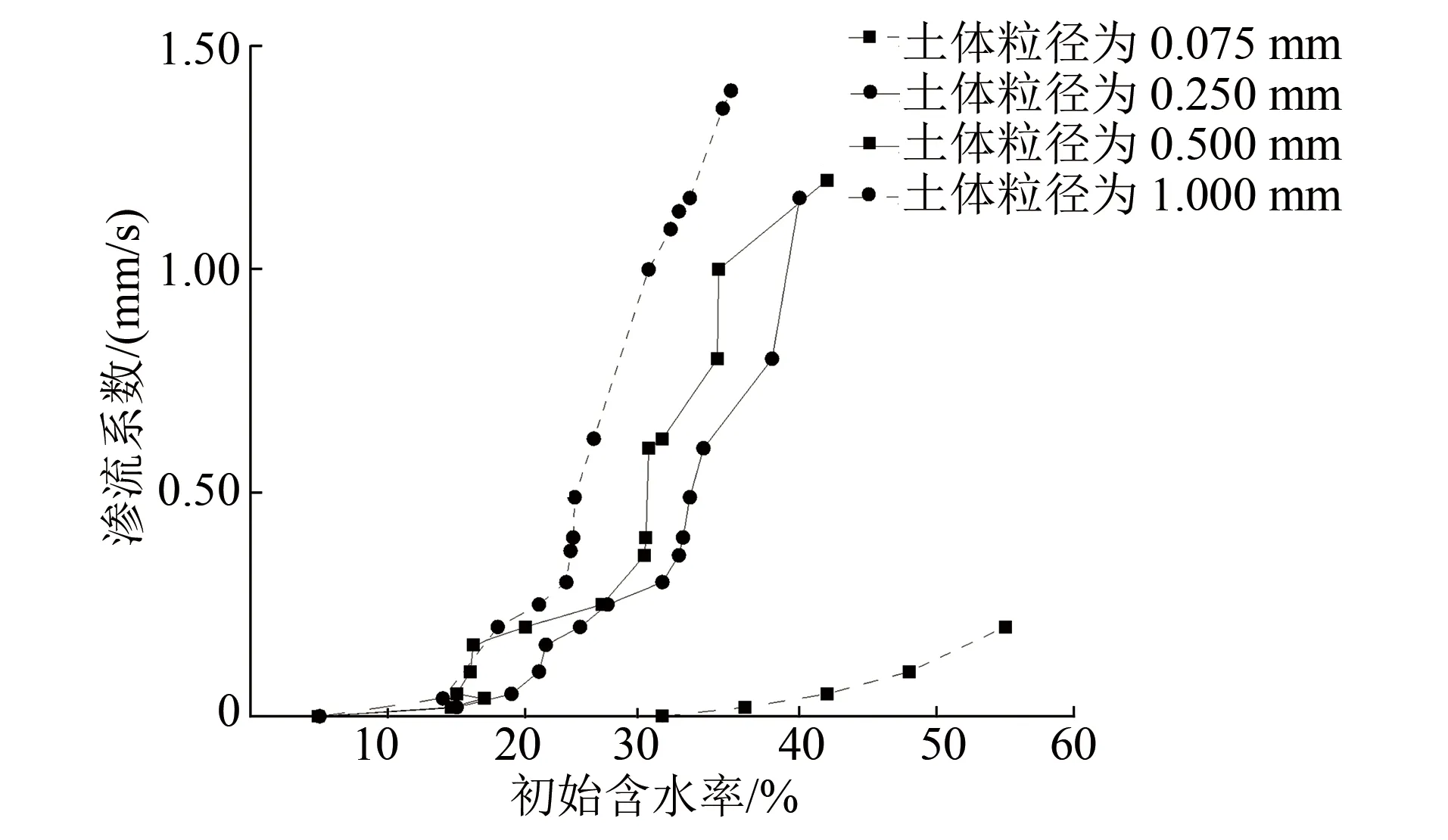
图2 不同粒径下土体渗流系数与初始含水率的关系

由图2可知:土体的粒径越大,渗流系数越大;土样的粒径为1.0 mm、初始含水率为34.8%时,其渗流系数最大,达1.40 mm/s;在同一粒径下,土样的渗流系数随初始含水率的增大而增大,当初始含水率达到一定程度后,初始含水率小幅增加,渗流系数有较大的增加,此时曲线的曲率随渗流系数的增大而减小。

为了更形象地呈现渗流系数随粒径变化的规律,绘制了初始含水率分别为15.1%、24.6%及32.6%时渗流系数随粒径的变化曲线,如图3所示。

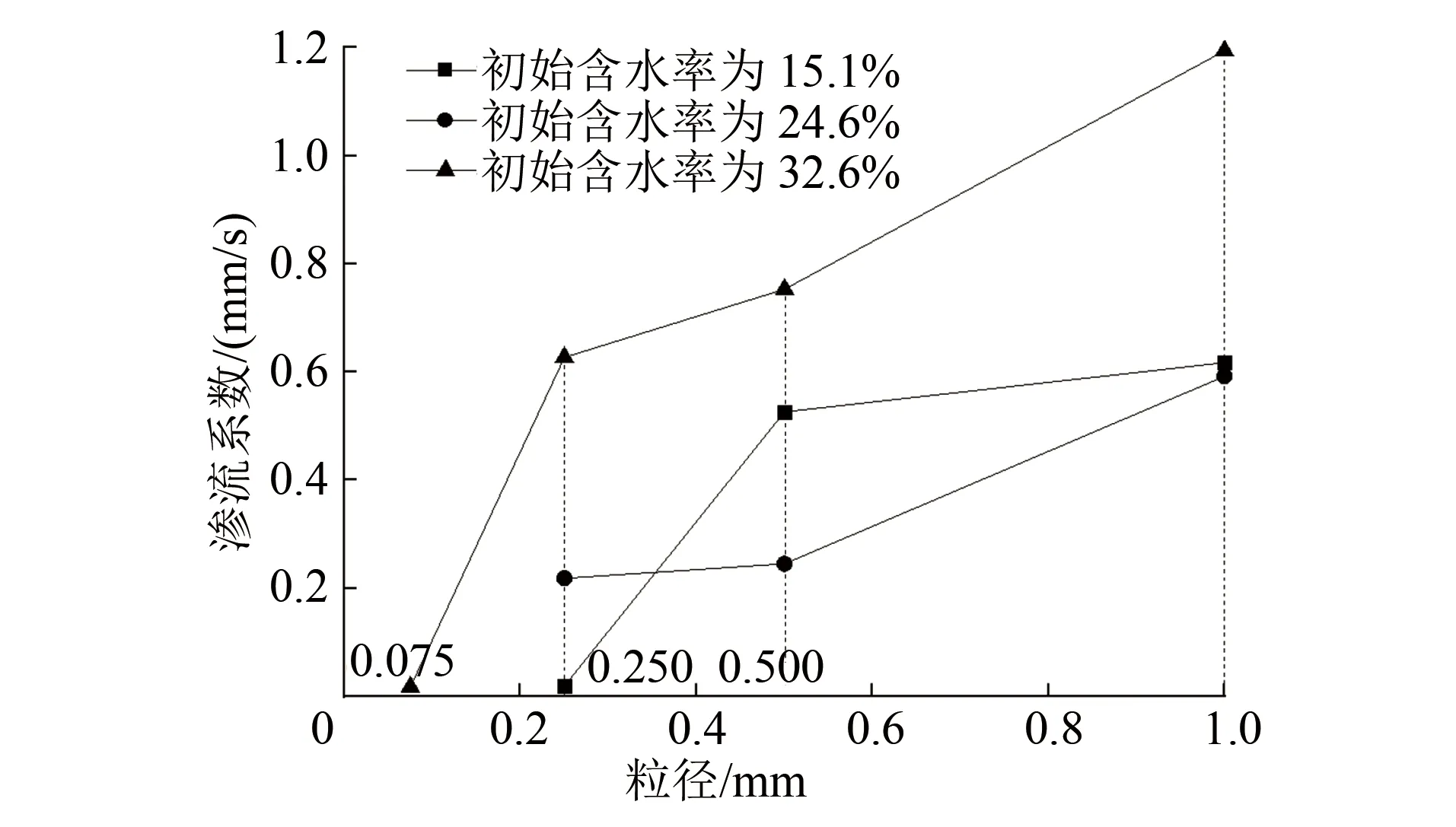
图3 不同初始含水率下渗流系数随粒径变化曲线

由图3可知:①初始含水率较大的土体其渗流系数也较大;②初始含水率较小的土体其渗流系数随初始粒径的变化并不明显;③相同的初始含水率下,粒径越大,渗流系数越大;④初始含水率为32.6%时,渗流系数达到最大值(1.194 mm/s);⑤粒径较大时,渗流系数随粒径的变化梯度较小,例如,初始含水率为15.1%的情况下,粒径由0.25 mm增加到0.50 mm时渗流系数增加了267.0%,而粒径由0.50 mm增加1.00 mm时渗流系数仅增加了17.3%。

2.2 土体饱和度对渗流系数的影响

土体饱和度S的计算式为:

S=γswGs/[Gs(1+w)γw-γs]

(1)

式中:

w——土体含水率;

γw——水的比重;

Gs——土体比重;

γs——土的重度。

通过改变含水量来实现不同饱和度土样的制备。式(1)中,Gs取2.75;用烘干法控制γw,以得到改变土体的γs,实现不同饱和度土样的制备。设uw为水的孔隙水压力,ua为土体内的气体作用力,则S对非饱和土中渗流的影响是通过液-气收缩膜平衡及基质吸力来实现的。本文选取3组不同S的土样(1#土样、2#土样及3#土样),测量各土样的uw。ua取标准大气压,即可得到这三组土样对应的基质吸力(1#土样基质吸力、2#土样基质吸力及3#土样基质吸力)。由此绘制出土体饱和度S与3种土样基质吸力的关系曲线,并与经典的饱和度与基质吸力Brooks &Corey曲线进行对比,如图4所示。

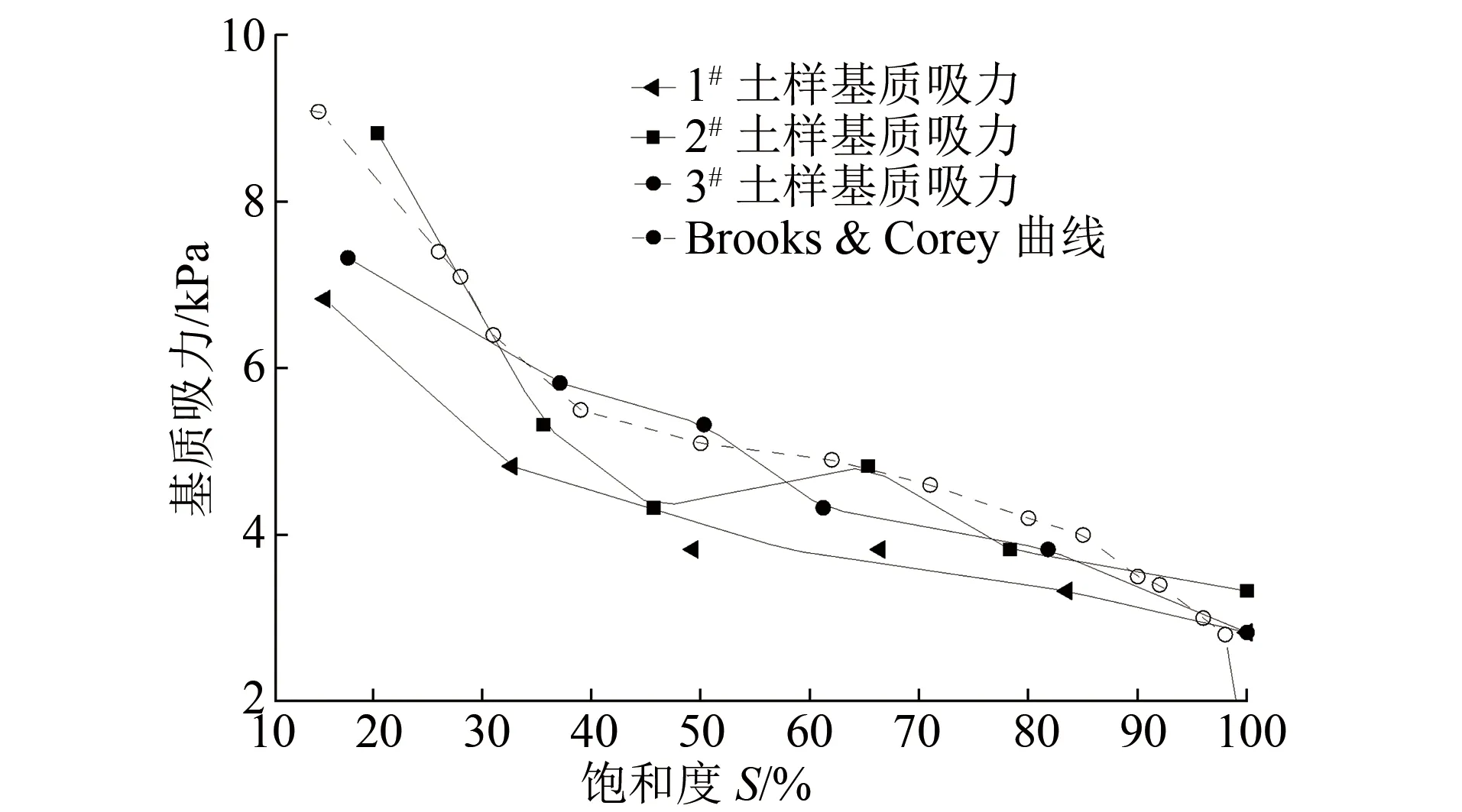
图4 香井区间3组测试土样的土体饱和度与基质吸力关系曲线

由图4可知:测试土样的关系曲线均呈递减形态,其形态与经典的Brooks &Corey曲线均较相似。当15%≤S≤45%时,基质吸力的变化速率均较大。当S≥60%时,基质吸力的变化趋势均变缓。

基质吸力与渗流系数之间的关系常用土水特征曲线来描述,典型的土水特征曲线呈“反S型”。将实测的三组土样数据采用以下数学模型进行拟合:

S=A1+(A2-A1)/[1+10[lg x0-(ua-uw)]ρ]

(2)

式中:

A1、A2、x0、ρ——拟合参数。

三组土样数据拟合后的决定系数R2分别为0.967,0.880,0.990,由此可认为拟合程度较好。数据拟合后绘制出三组土样对应的土水特征曲线,并与Brooks &Corey水土特征曲线进行对比,其结果如图5所示。由图5可知:当基质吸力达到一定程度后S的变化趋缓,将此时的饱和度定义为残余饱和度Sr,经计算,三组土样的平均残余饱和度为18.7%。

图5 三组土样的土水特征曲线

将剔除了残余饱和度后的饱和度定义为有效饱和度Se,设λ为拟合参数。只有当基质吸力达到一定程度,Se才有所变化,此时的基质吸力称为土体的进气值ub。Se与ub的关系为:

(3)

式(3)中,λ等于Se与基质吸力关系曲线的负斜率,可求得λ=0.205。设ks为饱和状态下土体的渗流系数,δ为土体孔隙特征系数,且δ=(2+3λ)/λ,则非饱和状态下土体的渗流系数kw与Se的关系为:

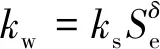
(4)

由此,绘制得到三组土样的基质吸力与有效饱和度Se的关系曲线,并与Brooks &Corey有效饱和度曲线进行对比,其结果如图6所示。由图6可知:只有在基质吸力足够大的情况下,气体才有足够的势能进入土体内,因此各分图上均出现了1个平台段。将平台段最右端处对应的基质吸力即为土体的进气值,3组土体的进气值分别为3.4 kPa、3.6 kPa及3.7 kPa。

2.3 渗流作用下土体强度变化情况

为测定非饱和土在水的作用下的强度变化情况,进一步对初始含水率分别为42.5%、24.5%、14.5%的土样实施直接快剪试验,计算得到其对应的内摩擦角分别为7.12°、9.25°及18.10°,黏聚力分别为15.5 kPa、22.5 kPa及24.5 kPa。由此可知:非饱和土体中的渗流作用使得不同含水率下土体的强度有所差异,含水率越大,土体强度越低。

3 渗流-应力耦合作用模块开发

3.1 渗流系数与饱和度的修正

3.1.1 渗流系数修正模块

由上文可知,取三组土体进气值的平均值为3.47 kPa,残余饱和度为18.7%,λ=0.205。基于式(3)及式(4),可得:

(5)

FLAC3D软件中,若土体中出现了负孔隙水压的单元,则认为该土体处于非饱和状态,此时的渗流系数应根据式(5)进行修正。其具体步骤为:①使用zone.next()命令遍历单元,使用zone.pp()命令读取上一个计算步骤结果中的孔隙水压力。孔隙水压力若为负值,则进入下一个步骤,否则结束本轮计算。②根据式(5),使用zone.fluid.prop(pnt,′permeability′)命令更改渗流系数,并开始新一轮的计算。

3.1.2 饱和度修正模块

随着孔隙水压力的变化,饱和度S会发生变化,应在计算中动态地修正饱和度,其计算式为:

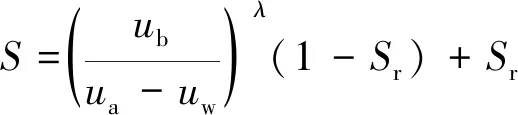
(6)

对S进行修正的具体步骤为:①用gp.next()命令遍历节点,再使用gp.pp()命令读取节点上一个计算步骤结果中的孔隙水压力。孔隙水压力若为负值,则进入下一个步骤,否则结束本轮计算。②根据式(6)计算饱和度,使用gp.sat(gnt)命令更改饱和度,并开始新一轮的计算。

3.2 围岩强度修正模块

根据文献[7]建立的二次弹性模量与等效塑性变形的数学模型进行围岩强度的修正,其具体步骤为:①使用zone.next()命令遍历模型所有单元,再使用zone.state()命令判断单元是否进入塑性状态。若进入塑性状态,则进入下一个步骤,否则结束本轮计算。②使用zone.strain.inc命令读取单元的应变张量,计算单元的塑性应变,再按照折减强度算出黏聚力和内摩擦角,使用zone.prop(pnt,′friction′)命令和zone.prop(pnt,′cohesion′)命令,对黏聚力和内摩擦角进行更改,并开始新一轮的计算。

3.3 有效性及合理性验证

本文利用FLAC3D软件建立了下穿马濠运河的模型,本构模型选取摩尔-库伦模型,其中:x轴为东西方向;y轴为开挖方向(向南取正);z轴为竖向方向(向上取正)。为消除边界效应,模型尺寸定为220 m(x向)×165 m(y向)×50 m(z向)。在模型上设置了3个监测断面及7个测点,如图7所示。

图7 模型中地面沉降监测断面及测点布置图

3.3.1 有效性验证

为了验证饱和度修正模块是否有效,模块应能识别出孔隙水压力为负值的单元和节点。为此,设置了未激活修正模块的模型。计算得到了该组土体的初始孔隙水压力分布状态,如图8 a)所示。由图8 a)可知,在香井区间的开挖过程中,掌子面与隧道下底板处的孔隙水压力明显为负值,这与实际施工情况是相符的。

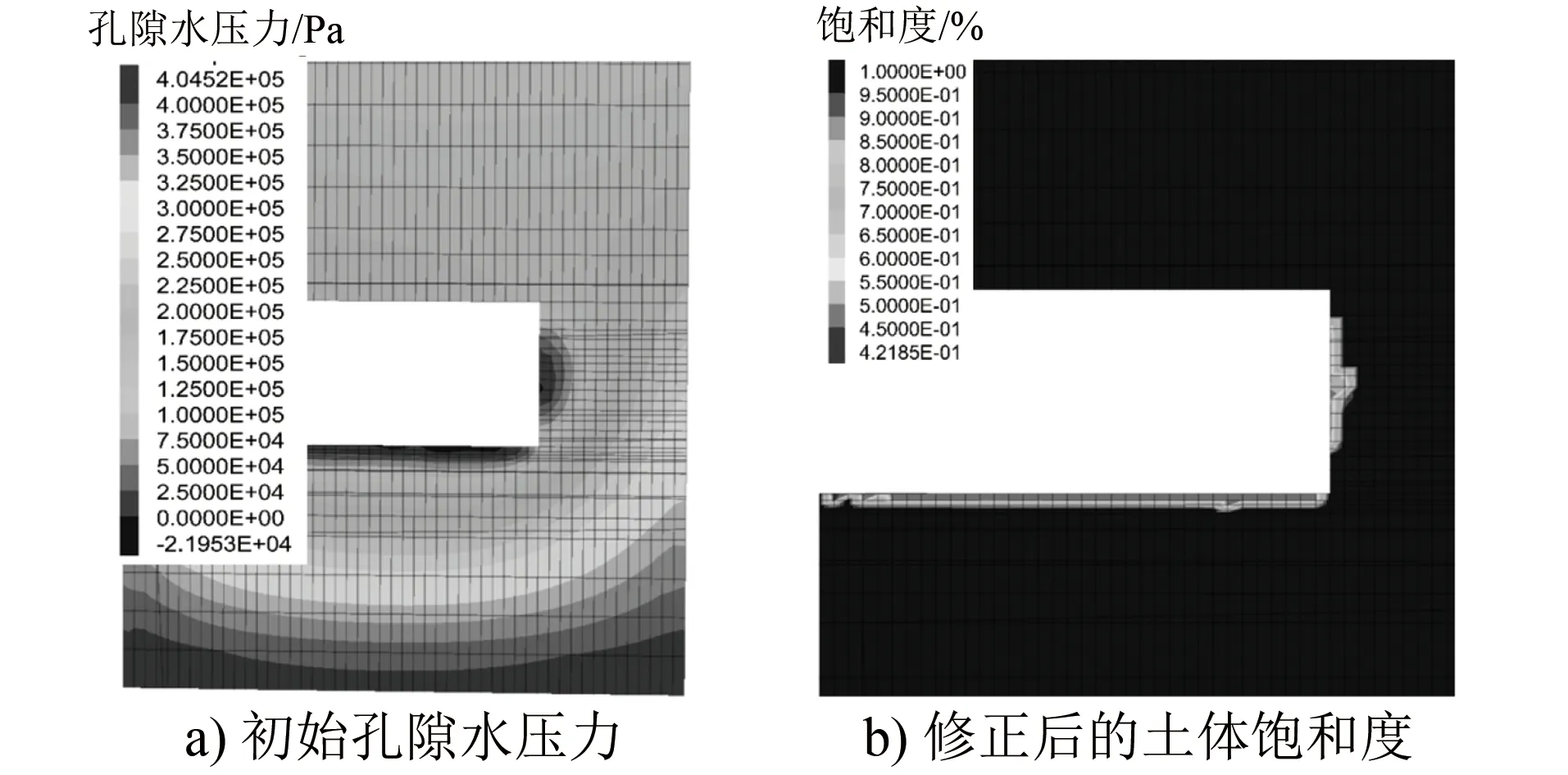
图8 饱和度修正模块的有效性验证截图

将修正模块激活,进一步模拟计算香井区间开挖过程中土体饱和度及渗流系数情况,其中,饱和度的分布情况图8 b)所示。由图8 b)可知,在隧道掌子面与底板位置处出现了明显的饱和度修正情况,这与图8 a)识别得到的土体情况结论一致。

3.3.2 合理性验证

选取3个监测横断面(见图7),其中:断面1为y=2.0 m处横断面;断面2为y=12.0 m处横断面,断面3为y=22.0 m处横断面。每个断面沿隧道中线对称设置7个间距均为10 m的地面沉降监测点。三个断面沉降曲线的实测值和计算值的对比如图9所示,横轴数据取往右线方向为正值。由图9可知,断面1、断面2及断面3计算值与实测值之间差值分别为8.2 mm、2.2 mm及1.9 mm。

图9 三个断面沉降的实测值与计算值对比

进一步对开挖过程中的孔隙水压力进行对比分析。施工过程中每开挖掘进4 m,测量一次掌子面中心处的孔隙水压力。每开挖掘进0.5 m,计算一次掌子面中心处的孔隙水压力。绘制这2个数据随开挖进尺(y向)变化的曲线如图10所示。由图10可知,孔隙水压力的计算值与实测值基本一致。

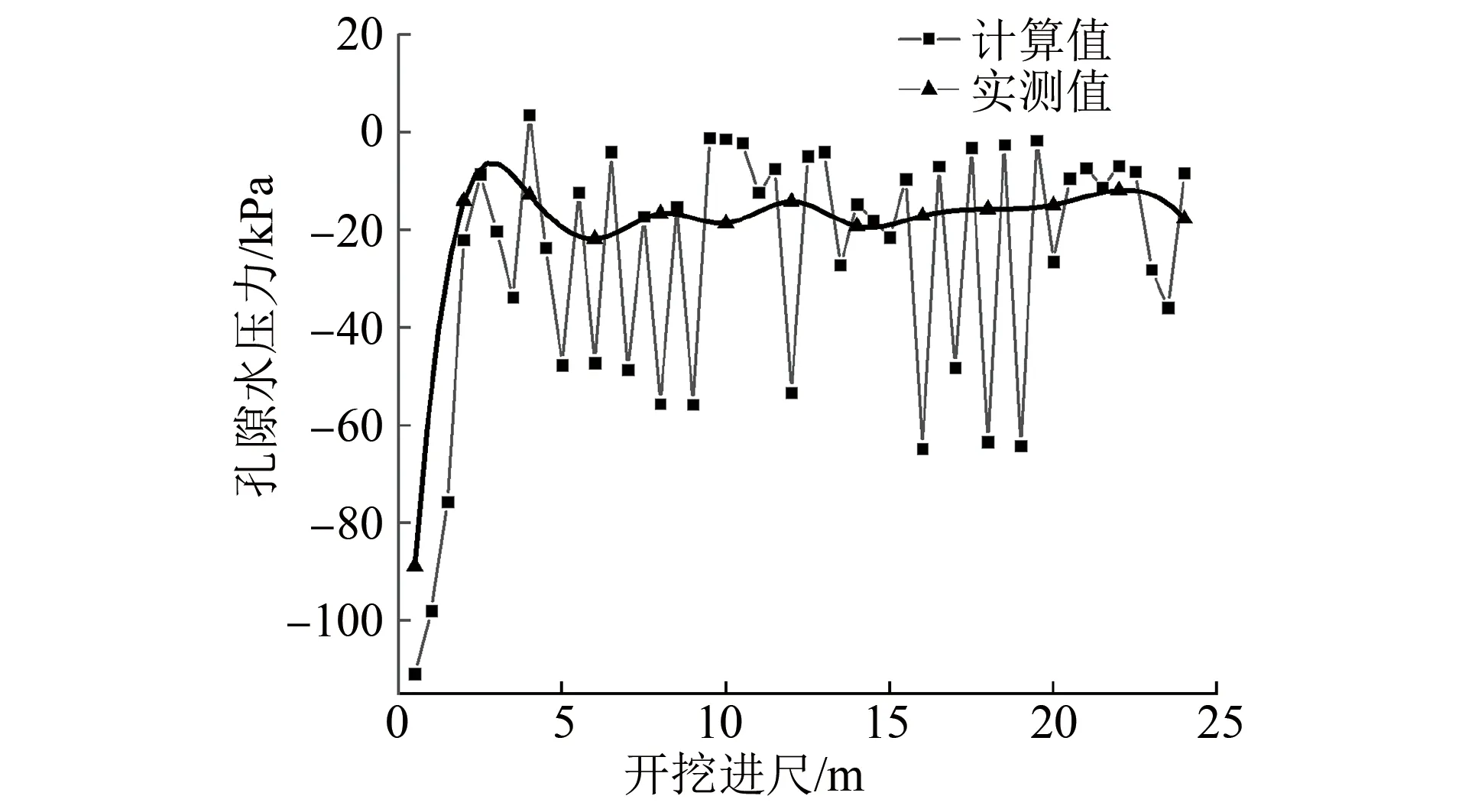
图10 孔隙水压力的计算值与实测值对比

4 计算值与实测值的对比分析

4.1 变形分析

图11为y=5.0 m、y=13.0 m及y=21.0 m处横断面在z向的变形云图。

图11 y=5.0 m、y=13.0 m及y=21.0 m处横断面在z向的变形云图

由图11可知:随着开挖进尺的逐渐增大,隧道整体垂直变形明显呈现不对称性;开挖初期,其最大变形出现在运河的西南方,从y=5.0 m处横断面看,最大变形也出现在运河的西侧;随着开挖进尺的推进,其最大变形逐渐向运河的东侧发展,从y=21.0 m处横断面看,最大变形值(2.520 mm)出现在运河东侧。

图12为y=12.5 m横断面处运河底板西侧、东侧的沉降曲线。由图12可知:随着开挖推进,底板东西侧变形先增大后逐渐减小,东侧的最大实测沉降值为2.68 mm,西侧的最大实测沉降值为2.59 mm;与计算值相比,实测值较为离散且数值稍大,这表明马濠运河实际的倾斜或扭转变形较模拟计算更明显。

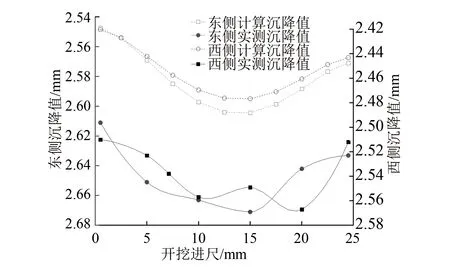
图12 y=12.5 m横断面处运河底板东西侧沉降变形

选取y=5.0 m、y=10.0 m、y=15.0 m及y=20.0 m处横断面的运河底板东侧、西侧的沉降数据,图13展示了不同开挖进尺下运河各横断面处西端沉降值和东端沉降值之差的发展趋势。由图13可知:4个断面中,运河底板东西侧沉降差均在开挖进尺大于5.0 m后变为负值,这说明开挖进尺大于5.0 m后东侧的沉降值开始大于西侧的沉降值;4个断面的曲线没有重合,而是上下错开,这说明不同断面处底板的东西侧沉降变形不一致,据此可推断马濠运河发生了一定的扭转变形。

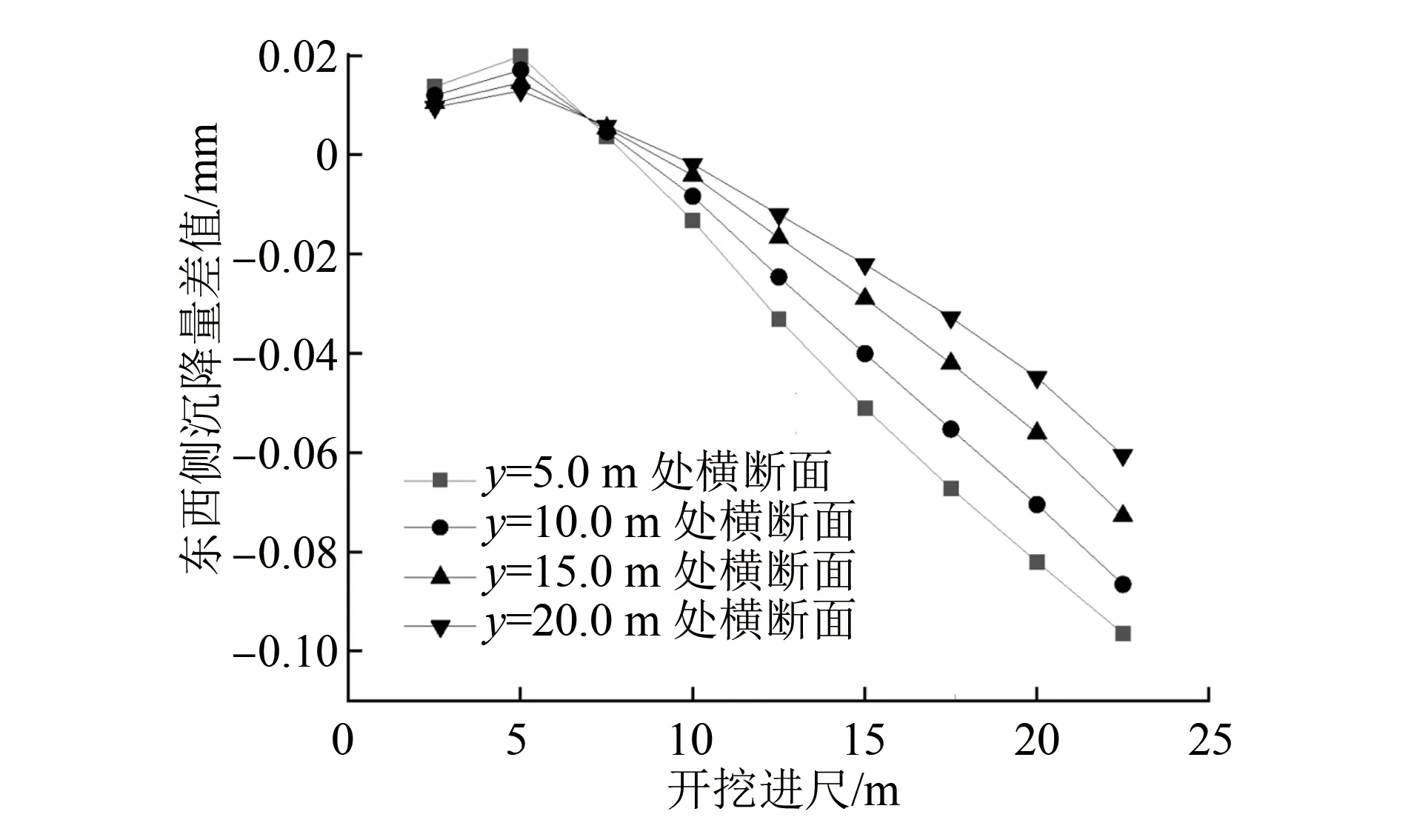
图13 运河底板不同断面处东西侧沉降量差值随开挖进尺的变化情况

4.2 渗流作用对运河变形的影响

在y=12.5 m处的横断面上,考虑与不考虑渗流-应力耦合作用下的盖板与底板处变形值计算结果如表2所示。由表2可知:不考虑耦合作用计算得到的变形绝对值明显比考虑耦合作用的变形绝对值小,其最大增幅为108%,这说明渗流作用对于古运河的变形影响甚大,无法忽略。

5 结论

1) 富水松散地层透水能力较强,且随着初始含水率的增大,渗透系数变大。当初始含水率达到25%时,含水率对渗透系数的影响更为明显,即含水率小幅增加将导致渗流系数大幅增加。同一初始含水率下,粒径越大,渗流系数越大。粒径较大时,渗流系数随粒径的变化梯度较小。

2) 通过对实测数据进行对比验证,以及实测数据在理论上的有效性验证,结果表明基于FLAC3D软件进行二次开发的渗流-应力耦合模块是合理、有效的。

3) 隧道下穿使得古运河结构发生了整体下沉,且运河底板东西侧还存在差异沉降,即结构承受了一定的因扭转引起的剪切力。考虑到运河年代久远,浆砌石在遭受侵蚀后,其强度有所折减,施工时应采取相应的保护措施。