地铁保护区内爆破施工对既有地铁隧道结构的振动影响

徐庆辉 吴 军 李 耀 闫 兵

(1.青岛地铁集团有限公司,266011,青岛; 2.上海勘察设计研究院(集团)有限公司青岛分公司,266199,青岛;3.中国海洋大学环境科学与工程学院,266101,青岛∥第一作者,高级工程师)

在青岛、大连等地质条件较好的地区,地铁保护区内进行基坑爆破开挖的情况逐年增多[1-3]。爆破会不可避免地对邻近的地铁隧道衬砌结构产生影响[4-5]。探究爆破振动对邻近地铁隧道结构的影响规律,是保障地铁运营安全的首要问题。

目前,隧道结构爆破振动响应规律的研究在工程监测、数值模拟和理论研究三方面均有一定成果[6-8]。在工程监测方面,文献[9]通过分析现场实测数据,指导现场装药施工,降低了掏槽孔爆破产生的地面振动效应。在数值模拟方面,文献[10]采用LS-DYNA有限元软件研究了球状药包爆破振动的特征,并给出了爆破振动助阵频率和平均频率的衰减规律;文献[11]通过数值模拟,探究了既有隧道扩建爆破过程中特征点的振动速度(下文简称“振速”)和衰减规律。在理论研究方面,文献[12]推导了爆破地震波作用下圆形地下洞室围岩的应力和位移表达式,求出了不同条件下围岩周围的应力和振速分布规律。

本文以青岛地铁保护区内基坑爆破施工具体案例为背景,采用数值模拟方法,研究基坑爆破开挖时既有地铁隧道衬砌结构对爆破地震波的动态响应规律,探索空间位置对该隧道衬砌结构振动响应的影响规律,以期在工程实践中对地铁隧道衬砌结构爆破振动响应规律有更为深入的了解,对爆破振动监测在监测点布设位置、监测范围等方面有所指导。

1 工程背景

拟建的青岛市某地下工程项目二期在建基坑(以下简称“二期基坑”)与既有地铁隧道(以下简称“隧道”)结构外边线的最小水平距离约为10 m,如图1所示。

结合青岛市特殊地质状况,该基坑拟采用爆破开挖方式。本工程所处场区内基岩以花岗岩为主,煌斑岩、细粒花岗岩呈脉状穿插其间,局部地段发育碎裂岩等构造岩。

2 数值模拟

2.1 建立数值计算模型

基于项目工程资料,运用ANSYS/LS-DYNA软件建立了显动力数值计算模型。如表1所示,拟设置四种工况,分别计算不同的爆源与隧道结构的距离(以下简称“爆距”),以及隧道与爆破中心(以下简称“爆心”)的夹角(以下简称“爆破角度”)下,爆破振动对隧道结构的影响。其中:工况一为实际施工工况;其余工况为虚拟假定工况。

表1 四种工况的设定

四种工况对应的数值计算模型如图2所示。模型尺寸为40 m(长)×5 m(宽)×30 m(高),隧道轴向长度为5 m。将模型上、下表面的右侧边界设为无反射边界,并在前后面施加法向约束。

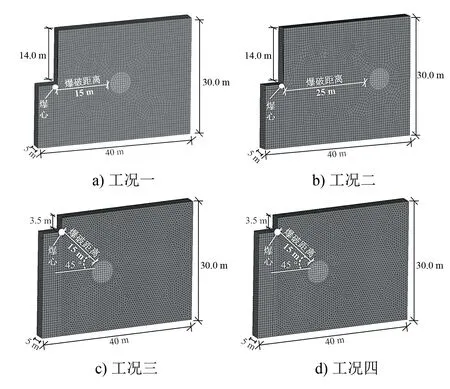
图2 四种工况对应的数值计算模型

2.2 参数选取

为简化计算,不考虑炮孔的布设方式,假定炸药为球状炸药。计算模型采用八节点实体单元,岩石材料和隧道衬砌结构使用*MAT_PLASTIC_KINEMATIC材料模型。模型的计算参数如表2所示。

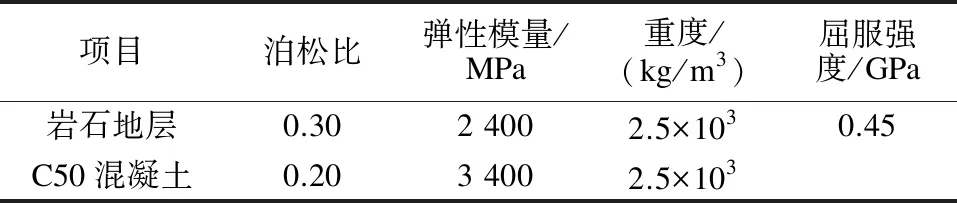
表2 模型的计算参数

炸药采用ANSYS/LS-DYNA软件中内置的高性能炸药,关键字为MAT_HIGH_EXPLOSIVE_BURN,炸药状态方程使用JWL状态方程。模型的炸药参数取值分别为:重度取1.63×103kg/m3;爆速取5 500 m/s;爆破压力取1×1010Pa。

工况一采用的爆破药量(以下简称“药量”)为工程实际药量(0.36 kg)。由于工况二、工况三及工况四为虚拟假定工况,本文基于实际爆破监测数据修正后的萨道夫斯基公式,以及运营期地铁爆破振速允许值控制在1.0 cm/s的要求,综合考虑地铁线路运营期间乘客的心理承受度,计算得到工况二、工况三及工况四下所需的药量分别为1.68 kg 、0.36 kg及1.68 kg。

2.3 隧道监测点选取

分别选取隧道环向的8个特征点(A1—A8)、纵向的8个特征点(B1—B8)进行振速及应力分析,各特征点的位置分布如图3所示。

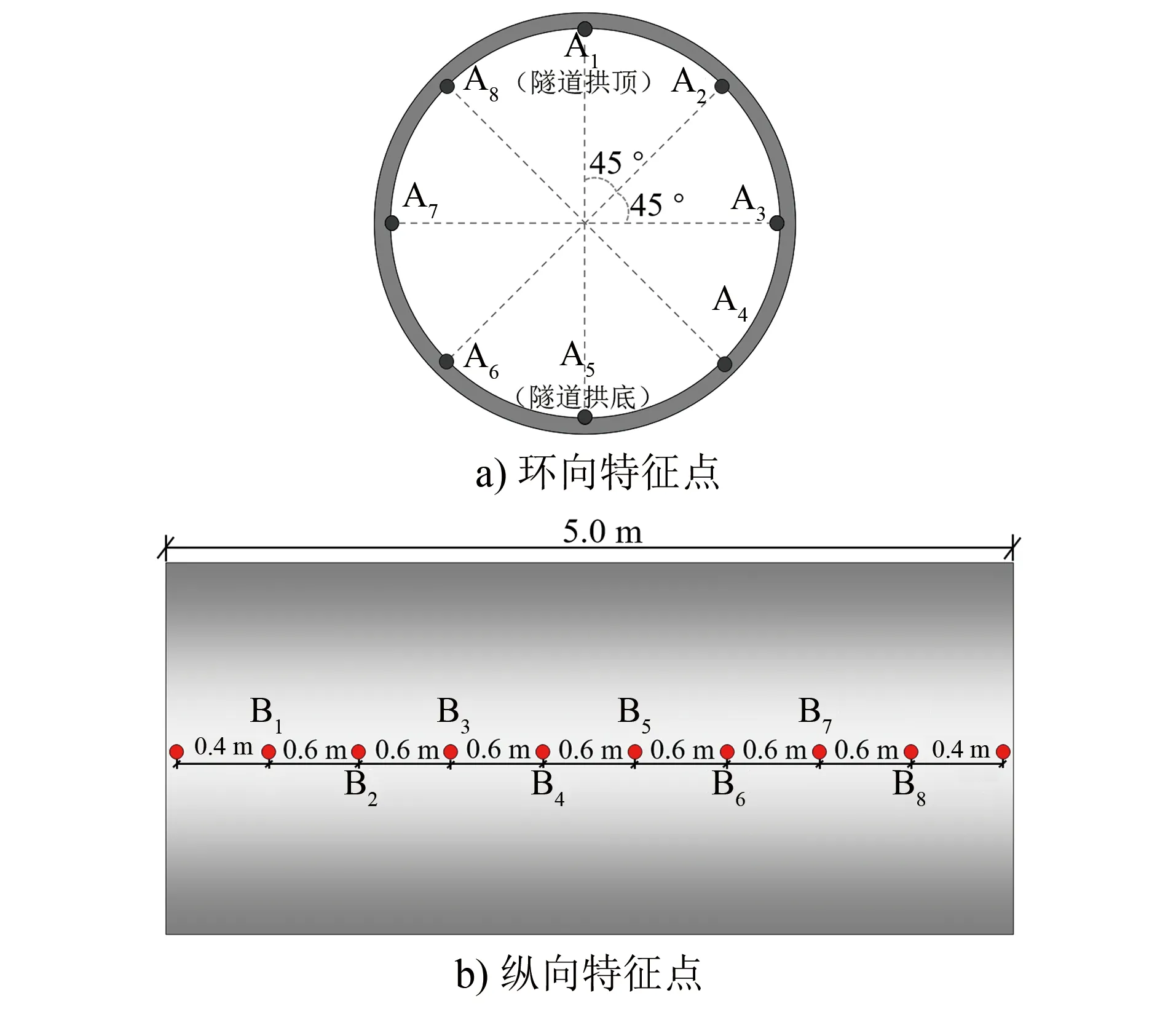
图3 隧道监测点的位置分布

3 模拟结果分析

3.1 环向隧道衬砌结构振速与频率响应特征分析

爆破产生的振动波经非常短暂的传播时间后对隧道产生影响。本文以工况二下的A7特征点为例进行分析。与其他环向特征点相比,A7为距离爆心最近的特征点,其振速衰减和变化幅度最大。设ti为振动波的传播时间,vmax,i为第Ai个特征点的振动速度峰值。

工况二下A7的振速时程曲线如图4所示。由图4可知:由于爆破振动波的影响,A7会在极短时间内到达振动峰值vmax,7,然后迅速衰减。直至下次振动波到来时,才会再次重复此规律。但是随着炸药能量释放完毕,衬砌结构监测点振动波的峰值会逐渐衰减,直至爆炸完毕。

图4 工况二下A7的振速时程曲线

各工况下,环向各特征点Ai的ti及vmax,i存在一定差异。为展现隧道衬砌振速响应规律,将四种工况下各特征点的振速峰值绘制于隧道轮廓外侧,如图5所示。

图5 四种工况下环向各特征点的振速峰值

对图5的四种工况进行对比,可知:

1) 各工况下,因爆心与衬砌结构的相对方位不同,环向8个特征点的振速峰值有所差异,各特征点振速峰值的最大值出现在距离爆心最近的部位(即A7处)。

2) 环向8个特征点中,振速峰值的最大值和最小值呈对角线分布,即:振动对迎爆面影响最大,对背爆面影响最小。

3) 爆破药量不同,爆破振速从迎爆面到背爆面的衰减幅度有所不同,小爆破药量条件(工况一及工况三)下背爆面的振速峰值为迎爆面的20%～30%,大爆破药量条件(工况二及工况四)下背爆面的振速峰值约为迎爆面的50%。

3.2 环向隧道衬砌结构应力响应

爆破振动会使隧道结构受到动态的压缩和拉伸,不同位置对爆破振动的响应时间和响应程度也不尽相同。图6为工况二爆破过程中A1及A7处的拉应力变化情况。由图6可知:爆破振动最先对迎爆面产生影响;随着时间的推移,爆破振动逐渐影响拱顶和拱底, 最后影响背爆面; 受爆破振动的影响,隧道衬砌结构2个特征点处的拉应力均呈现迅速增大至峰值后逐渐衰减的规律。

图7描述了整个爆破过程中四种工况下隧道衬砌结构环向各特征点的拉应力分布变化情况。如图7所示,以工况二为例,分析如下:

1) 迎爆面的拉应力普遍高于背爆面的拉应力,背爆面的结构拉应力值约为迎爆面的40%～50%。

2) 隧道结构受到的最大拉应力为0.92 MPa。根据GB 50010—2010《混凝土结构设计规范》,C50混凝土抗拉设计强度值为1.89 MPa,隧道结构的拉应力未超过混凝土设计强度值,这说明爆破振速为1.0 cm/s时,隧道衬砌结构发生拉裂破损的可能性很小。

3.3 纵向隧道衬砌结构振速与应力响应分析

对隧道衬砌结构的纵向8个特征点(见图3 b))对应的8个断面进行分析。其中,B4—B5的中点处与爆源的距离最近。每个测点断面均选取四个环向特征点开展分析,其中:工况一及工况二选取A1、A3、A5、A7的四个环向特征点;工况三及工况四选取A2、A4、A6、A8四个环向特征点。各测点断面选取特征点的振速及应力数值计算结果如图8所示。

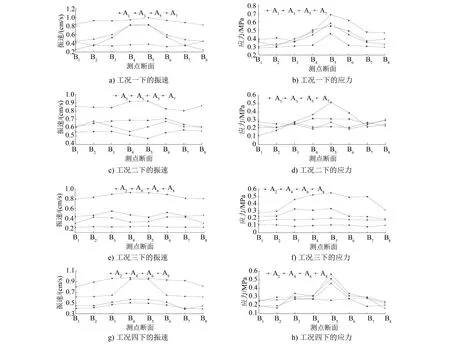
图8 各测点断面选取特征点的振速及应力数值计算结果

由图8可知:

1) 振速和应力总体呈现由爆距最小处向两侧衰减的规律,且二者分布规律呈现出一致性;工况一、工况二的振速峰值出现在B5断面A7处,分别为1.01 cm/s和0.92 cm/s,其应力最大值也出现在B5断面A7处,分别为0.69 MPa和0.52 MPa;工况三、工况四的振速峰值出现在B4断面A8处,分别为0.97 cm/s和0.93 cm/s,其应力最大值出现在B5断面A8处,分别为0.52 MPa和0.57 MPa。

2) 隧道两端个别特征点的振速和应力值出现了较小幅度的增加,这主要是因边界条件限制,振动波和应力波在模型边界处的正常传播受到了一定的影响。

3.4 现场实测与数值模拟结果拟合度分析

对工况一开展了现场监测,以获取爆破施工过程中隧道衬砌结构的振动数据,进而验证数值模拟计算结果的准确性。工况一下,取与爆心距离最近B5断面,在断面上设了两个监测点(测点1位于隧道右拱腰A3处,测点2位于隧道左拱腰A7处),这两个测点在B5断面的两拱腰处正对布设,得到的实测振速值如图9所示。

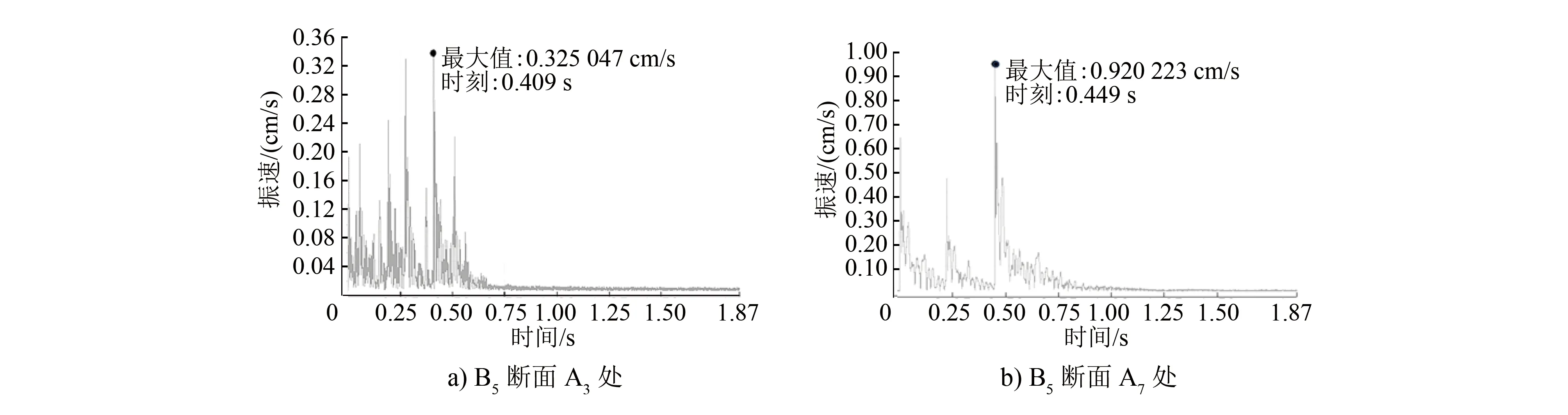
图9 工况一下B5断面A3及A7处的振速实测值

仍以工况一为例,取B3、B5、B7三个断面A3、A7处振速的模拟值与实测值进行对比,其结果如表3所示。

表3 工况一下B3、B5、B7断面监测点振速的模拟值与实测值对比

由表3可知:各测点的振速差值率均在8.77%～13.10%范围内,这说明模拟结果能够较好地反映实际施工爆破对隧道衬砌结构的影响。模拟值较实测值偏高,其主要原因为数值模拟时将地层设为均一、连续地层,而现实地层中可能存在破碎带、软弱面等不良地质体,因此爆破振动波在现实地层中传播时振速有所减弱。

4 结语

本文运用ANSYS/LS-DYNA软件,结合工程实践,模拟了基坑爆破开挖对邻近既有地铁隧道的动态影响,分析了爆破荷载条件下隧道结构的爆破振动响应规律,得到结论如下:

1) 受邻近爆破影响,隧道衬砌结构各点在极短时间内达到振速峰值,然后振速迅速衰减;振速峰值均出现在距离爆心最近的衬砌结构部位。

2) 振速最大值和最小值总体呈对角线分布,隧道衬砌结构迎爆面振速最大、背爆面振速最小;爆破药量越大,爆破振速从迎爆面向背爆面衰减幅度越大。

3) 在爆破荷载作用下,隧道衬砌混凝土应力场呈现动态变化,背爆面结构拉应力值约为迎爆面结构拉应力值40%～50%。

4) 振速曲线和应力曲线总体上均呈现从爆距最小处向两侧衰减的规律,且振速分布规律与应力分布规律具有一致性。

5) 开展保护区地铁隧道结构爆破振动监测时,监测点的位置宜选取在距爆心最近处,并随着爆心方位的变化及时更换监测点的布设位置;在爆破振速控制指标(1.0 cm/s)下,隧道衬砌结构产生的附加应力对衬砌结构带来损伤的可能性较低;对于已开通运营的地铁隧道,考虑到乘客的舒适度与心理接受度,建议采用更为严格的爆破振速控制指标。