滑坡监测中无线传感器网络节点部署的虚拟力算法

彭艳周, 高嘉呈, 程宙强, 吕俊达, 高德军

(1. 三峡大学 防灾减灾湖北省重点实验室,湖北 宜昌 443002; 2. 三峡大学 土木与建筑学院,湖北 宜昌 443002; 3. 国网湖北送变电工程有限公司,湖北 宜昌 443002)

关键字：滑坡监测; 区域覆盖; 无线传感器网络; 节点部署; 虚拟力算法

滑坡是一种广泛分布且破坏性强的地质灾害,给人类社会造成了巨大的人员伤亡和经济损失。其造成的损失并不是完全无法规避的,只要采取有效的监测手段,就有可能及时预测滑坡灾害并做出应对措施。传统的滑坡监测主要是利用滑坡区域内布置的各种传感器进行测量,并通过有线传输将测量数据传至现场的监控端[1]。但传统方法成本高、实时性差、易受空间等因素的制约,因此许多学者将无线传感器网络(wireless sensor network,WSN)技术应用到了滑坡监测工作中[2-5]。在应用过程中,需要将网络节点部署在滑坡地表,并且尽可能地覆盖更多的监测区域。合理的节点部署方案能够显著增加网络的覆盖率,提升网络的监测效果。目前,在滑坡监测中部署节点时仍然以手动部署为主,在面对复杂的部署任务时费时费力且效果不佳,合适的自动算法能够更为高效地解决节点部署的问题。

自WSN技术问世以来,许多学者就展开了其节点部署算法的研究,所提出的节点部署算法可分为四种类型:虚拟力方法[6]、几何方法[7-9]、智能算法[10-12]和多种方法的混合算法[13-15]。其中,虚拟力方法计算量小、优化效果明显、适用范围广,不仅能够用于WSN节点的部署,其分布式计算的特点还使其能用于移动无线传感器网络节点的自部署[6]。谭励等[16]针对空中传感器网络的能耗与环境问题,提出了加权虚拟力算法以及相应的扩散模型。Rout等[17]研究了复杂环境下的节点部署问题,提出了一种在关注区域内部存在障碍时使用的节点部署算法,该算法在原虚拟力算法的基础上细化了障碍物对节点的虚拟力,优化了节点对障碍物的规避。Sallam等[18]研究了各种节点数和节点覆盖半径情况下,如何为虚拟力算法设置合适的斥力和引力。Boufares等[19]基于虚拟力算法,提出了在三维倾斜平面上的移动传感器节点部署方法,该方法可实现网络在三维倾斜平面上的完全覆盖,并保证网络的连通性。Jiang等[20]针对水下移动传感器网络的节点部署问题,在虚拟力算法的基础上,提出了RBVF算法和VFRBEC算法。张俏薇等[21]对虚拟力算法的步长系数进行了研究,提出了基于sigmoid函数的步长系数。滕志军等[22]推导了虚拟力强度系数的计算方式,引入了节点密集度的概念,根据密集度来选择最优距离阙值。Sha等[23]提出了环形场的虚拟力算法,可以平衡各节点之间的工作负载,延长网络寿命。Liu等[24]将空气分子理论应用到虚拟力算法中,通过分子间的引力使节点集中在一定范围内,基于节点的正六边形分布设置了相邻、次相邻的零重力点,该方法能够快速有效地修复覆盖盲区,并提升网络覆盖率。

从上述的已有研究来看,现有研究多是在规则的二维理想平面或三维全空间中部署节点,可用于厂房、森林、水下等应用场景。但以上算法并不适用于在滑坡地表部署WSN节点。在滑坡监测工作中,节点只能被部署在滑坡区域的地表。这些地表通常是具有不规则起伏的三维曲面,且其边界的形状较为复杂。然而,已有的二维平面的部署算法难以适应复杂的边界形状,监测区域的地表坡度还会导致节点之间出现覆盖盲区,而三维全空间的部署方法显然不适用,因为WSN节点无法被部署在被监测区域的空中或是地底。

针对以上问题,本文以传统虚拟力算法为基础进行改进,提出一种适用于滑坡监测中节点部署的虚拟力算法(virtual force algorithm for the node deployment in landslide monitoring, LMVFA),在不同部署区域(多种形状的二维平面、三个三维曲面)进行了节点的模拟部署,验证了该算法在复杂的滑坡区域中部署WSN节点的有效性。

1 问题与假设

1.1 地形起伏与边界问题

在滑坡区域进行节点部署时,监测区域的地形起伏和边界问题是不容忽视的。如果忽视滑坡坡度,直接按照平面进行节点的部署,会导致节点之间出现覆盖盲区,见图1。

图1 覆盖盲区示意图Fig.1 Schematic diagram of uncovered area

在实际应用中,通常仅需要对指定的监测区域进行覆盖,如果不考虑边界问题,会导致大量节点被部署到监测区域之外,无法发挥作用。

1.2 系统模型

假设滑坡地表面是一个三维曲面,在单个节点的覆盖范围内,地表的变化幅度不明显。滑坡监测区域即为节点部署算法的关注区域(region of interest,ROI),其边界由若干边界点所确定,见图2。

图2 滑坡监测中节点部署的ROIFig.2 ROI of node deployment in landslide monitoring

节点覆盖区域的计算是一个困难的连续性问题,文献[19]证明了可以将其转换为离散性问题进行计算。将ROI离散化为若干个网格,以每个网格的中心点代表该网格区域,网格尺寸越小,计算精度越高。则ROI可以被表示为若干个网格中心点的集合{p1(x1,y1,z1),p2(x2,y2,z2) , ……},ROI上任意两点之间的欧式距离dij为:

(1)

本文采用二元感知模型(binary sensor model,BSM)进行节点覆盖的判定,并假设每个节点均具有球形的感知范围,当网格中心点p与节点ni的距离d(ni,p)小于等于节点的覆盖半径R时,该网格区域的事件被节点检测到的概率为1,否则检测到的概率为0,见式(2)。

(2)

若节点ni与节点nj之间的距离小于等于节点的通信半径C,则两节点之间视为连通,见式(3)。节点的通信半径C需满足C≥2R。

(3)

2 改进的虚拟力算法LMVFA

在虚拟力算法中,节点会受到各种虚拟力的作用,在虚拟力合力影响下,不断调整自身位置,使节点分布均匀,提升网络的覆盖率。

传统虚拟力算法中,多是以理想平面矩形为部署区域,以滑坡监测中的监测区域为部署区域时,由于地形起伏和边界形状,虚拟力平衡状态并不是网络覆盖率最高的状态。针对此问题,本文对虚拟力的计算方法进行了改良,进一步提升了网络的覆盖率。

2.1 节点间虚拟力

节点间虚拟力能够根据节点间的距离调节节点的移动方向与移动步长,使相邻节点不会过于接近造成覆盖区域的大量重叠。以两节点在三维空间中的欧式距离计算虚拟力,能够更好地根据滑坡区域的地形起伏来调整节点间距离。

由于节点只能部署在滑坡地表,在根据节点所受虚拟力更新节点位置时与三维全空间的虚拟力方法有所不同,需忽略节点在重力方向的移动,使得所有节点仅在水平方向上的X轴与Y轴方向进行移动,节点的Z轴坐标由其所处位置的地表高程所决定,因此,在计算节点受到的虚拟力时无需计算其在Z轴上的分量。

在传统虚拟力算法中,节点间虚拟力通常包含引力与斥力。本文仅考虑节点间的斥力与边界对节点的斥力,而不考虑引力。一方面,可以避免引力破坏最佳的平衡状态,降低网络的覆盖率。另一方面,滑坡监测中通常要求网络具有较高的覆盖率,投入的节点数量较多,即使没有节点间引力也不容易出现网络连通性问题,模拟结果也证实了这一点。

对于任意节点i和j,只要节点间距离dij小于距离阙值du,两节点间就会产生斥力。节点i的受到的来自其他节点的虚拟力的合力Fpi= (Fpix,Fpiy),见式(4)。

(4)

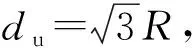
图3 距离阙值Fig.3 Distance threshold

2.2 边界对节点的虚拟力

在实际应用中,部署区域的边界问题通常是不容忽视的,因为仅需要覆盖指定的监测区域,区域外的覆盖是无效的。然而,许多已有研究中并没有充分考虑边界问题,对边界的讨论也多是针对简单的二维平面矩形。文献[25]所用的势力场方法可以适用于各种复杂形状边界,但不能最大化网络覆盖率,节点与边界之间存在较多的覆盖盲区。文献[17]提出的避障虚拟力算法在ROI为矩形时表现良好,在ROI为多边形时存在一些问题:单个节点覆盖范围内存在多段边界且内角较大时,其边界虚拟力合力的大小偏大,导致节点与边界之间存在较大的覆盖盲区;在内角较小处边界虚拟力过小,靠近边界的节点可能会被其他节点直接排斥到ROI以外;对于凹多边形,其直接计算节点至边界距离的方法也不适用。

针对滑坡监测中常见的ROI边界形状,本文提出的边界虚拟力计算方法为如下。

1) 搜索所有ROI边界外围的网格,将搜索得到的所有网格的中心点构成的集合称为E,见图4(a)。

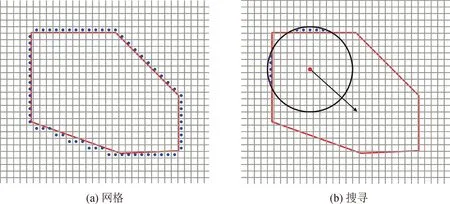
图4 边界对节点的虚拟力Fig.4 Virtual force of boundary to node

2) 对于节点i,搜寻E中所有与节点i的距离小于阙值db的点{e1,e2, …},根据式(5)计算其对节点的虚拟力Fei= (Feix,Feiy),见图4(b)。边界虚拟力的距离阙值db的取值是基于虚拟力平衡状态下,网络覆盖率最高来确定的,当du=2R时距离阙值db=R。

(5)

式中dei指ROI边界外围网格中心点到节点i的距离。

3) 边界对节点i的虚拟力的方向,即为{e1,e2, …}对节点i的虚拟力合力的方向。以{e1,e2, …}对节点i的虚拟力中的最大值max{|Fe|},作为边界对节点i的虚拟力大小。节点i受到的来自边界的虚拟力Fbi= (Fbix,Fbiy)为:

(6)

2.3 更新节点位置

节点i受到的虚拟力合力Fi在X轴和Y轴上的分量为:

(7)

随机生成的初始节点位置可能会出现节点间非常接近的情况,根据式(4),节点间的斥力会非常大。节点在每次迭代中的移动距离与其所受到的虚拟力有关,过大的斥力可能导致节点在一次移动中直接移动到边界之外,影响计算结果。因此将节点所受虚拟力的最大值限制为Flimit。对于节点i,其受到的虚拟力合力Fi为:

(8)

在虚拟力合力的作用下将节点i从原位置(xn-1,yn-1,zn-1)更新到新位置(xn,yn,zn),其中zn是由ROI的地形决定的:

(9)

式中α是步长系数,算法在逼近最优解后,不可避免地存在震荡现象,引入线性递减函数α作为步长系数可以显著改善这一点,使得节点随迭代次数的增加而逐步逼近最优解的位置,α的计算方式见式(10)。其中nmax为最大迭代次数,ns为开始递减时的迭代次数,本文取ns=nmax/2,使得节点在前期能够迅速扩散,加快收敛速度,后期逐渐减小移动步长,使节点向最优解位置不断逼近。

(10)

2.4 算法伪代码

综上所述,本文对传统虚拟力算法进行了改良,提出了应用于滑坡地形的改良虚拟力算法LMVFA,以滑坡区域进行节点部署时,该算法可以更好地提升网络的覆盖率。算法实现的伪代码如下。

输入:ROI,边界点集E,节点数量M,覆盖半径R,通讯半径C,距离阙值du与db,虚拟力强度系数cp,最大虚拟力Flimit,最大迭代次数nmax,节点初始位置Xs

输出:节点部署位置X,网络覆盖率,网络连通性,节点历史位置Xh

1: for n = 1 :nmax

2: //计算节点所受虚拟力

3: fori = 1 : M

4: 根据式(4)～(8)计算Fi

5: end

6: //更新节点位置

7: fori = 1 : M

8: 根据式(9)、(10)计算Xi

9: end

10: Xh[n] = X // 保存节点历史位置

11: end

12:根据式(2)、(3)计算网络的覆盖率与连通性

3 算例验证

本文在MATLAB环境下实现了上述算法,在多种监测区域下进行了节点部署,同时使用避障虚拟力算法(obstacle avoidance virtual force algorithm, OAVFA)[17]与虚拟分子力算法(virtual molecular force algorithm,VMFA)[24]作为对比,以验证本文提出的LMVFA的性能。

节点的初始位置是随机生成的,每次计算结果都有可能不同。因此,在计算时会重复计算100次并从中选出最优解,以尽可能地消除随机初始位置带来的不利影响。

3.1 二维形状

为了验证LMVFA在各种边界形状下的性能,考虑到ROI可能出现的各种内角情况,使用了正三角形(TRI)、矩形(REC)、正六边形(HEX)、正十字形(COS)、V形(V)、C形(C)等多种二维平面形状作为ROI进行节点部署,见图5,所有部署区域的面积近似相等。算法的参数见表1。

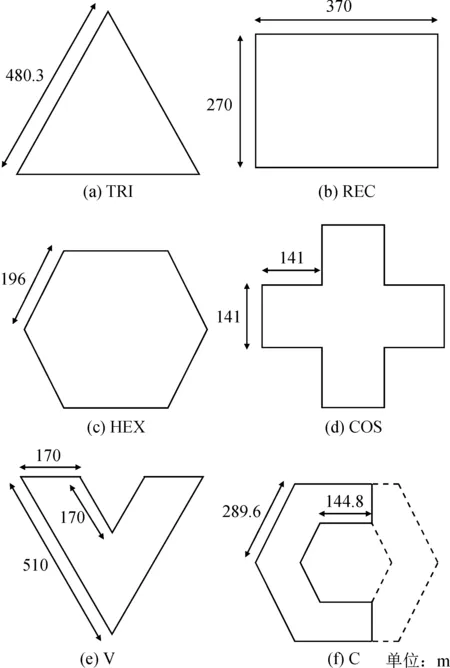
图5 作为ROI的二维形状Fig.5 2D shape as ROI

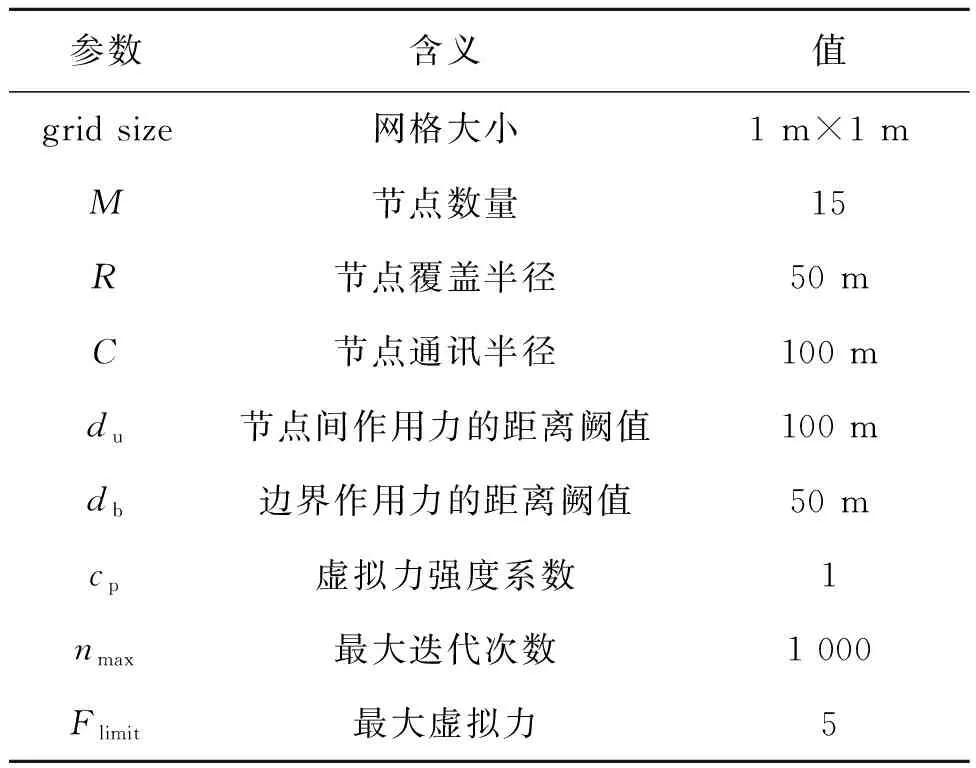
表1 算法的参数(二维形状)

图6显示了以多种二维形状作为ROI时,分别使用LMVFA、OAVFA和VMFA部署网络的覆盖率。在各种二维形状中部署节点时,LMVFA部署的网络在覆盖率上均优于其他2种算法,尤其是在十字形区域中,由于该区域的边界形状存在多个大于90°的内角,且内角处的边界作用力所影响的区域较为集中,在此情况下,LMVFA对边界虚拟力计算方法的改良表现出更为明显的优势,因此在网络的整体覆盖率上相差更大。

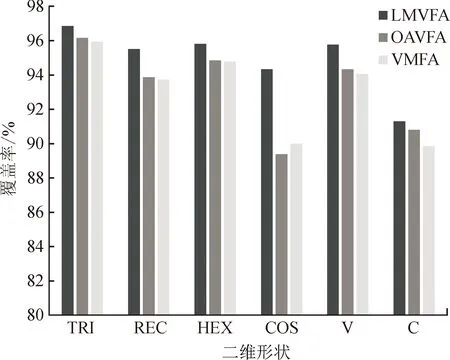
图6 二维形状中不同算法的网络覆盖率Fig.6 Network coverage of different algorithms in 2D shape

3.2 滑坡区域

为了验证LMVFA在各种滑坡区域中的性能,选取了3个滑坡区域[26-28]作为ROI进行了计算,滑坡区域的地形与边界见图7,算法的参数见表2。作为ROI的3个滑坡区域在边界形状、坡度、面积上都有一定差异,能更好地反映算法在各种滑坡区域中的性能。

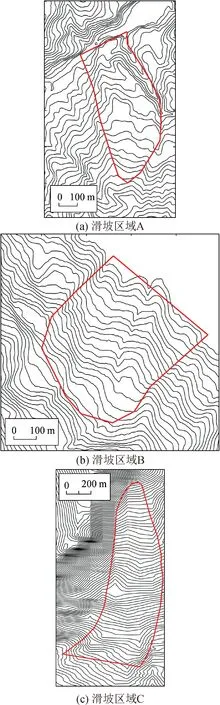
图7 滑坡区域的地形示意图Fig.7 Topographic map for landslide area

表2 算法的参数(滑坡区域)

3个滑坡区域的面积相差较大,而滑坡监测中通常要求网络具有较高的覆盖率,因此在3个滑坡区域中投放了不同数量的节点。其中,滑坡区域C由于面积较大,且整体形状较为狭长,在最大迭代次数为1 000无法完全达成虚拟力平衡状态,因此将其最大迭代次数增加到2 000。在实际应用中,可以通过调整虚拟力强度系数cp来加快虚拟力的平衡过程,此处为了便于将LMVFA与其他两种算法进行比较,仅增加了最大迭代次数nmax。

图8显示了以3个滑坡区域作为ROI时,分别使用LMVFA、OAVFA和VMFA所部署网络的覆盖率。可以看出,LMVFA部署的网络在覆盖率上均优于其他2种算法。

图9显示了分别使用3种算法时,网络的覆盖率随迭代次数的变化情况。初期OAVFA的网络覆盖率增长得更快,但很快就陷入节点震荡状态。LMVFA和VMFA的覆盖率则随着迭代次数的增加稳步增长。

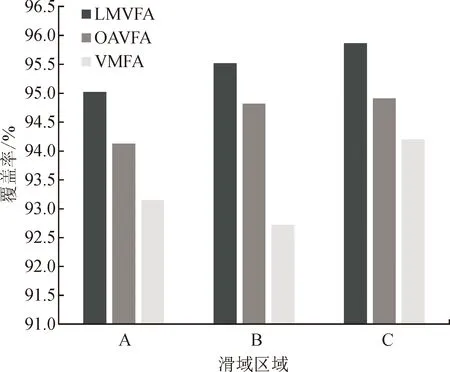
图8 滑坡区域中不同算法的网络覆盖率Fig.8 Network coverage of different algorithms in landslide region

图9 网络覆盖率随迭代次数的变化Fig.9 Change of network coverage with the number of iterations

滑坡区域的俯视图与LMVFA所部署网络中各节点间的连通路径见图10。从总体上来看,网络中没有孤立的节点,且大多数的节点均具有多条连接路径,在实际应用中能较好地应对单一节点的突发故障,而不至于造成大量节点的失联,可以说明LMVFA部署的网络具有较好的连通性。

4 结 语

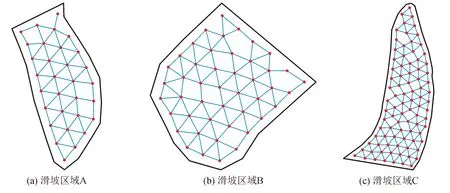
图10 网络的连通性Fig.10 Network connectivity

本文对滑坡区域中部署WSN节点的方法进行了研究,提出一种改良的虚拟力算法——LMVFA。该算法以网络覆盖率为优化目标,能够完成各种滑坡监测区域的节点部署任务。在多种形状的二维平面区域和三个不同的三维曲面区域(滑坡监测区域的地表)中进行WSN节点的模拟部署,计算结果表明,在网络覆盖率方面,LMVFA优于已有的虚拟力算法OAVFA与VMFA。

本文提出的算法仅适用于单个节点的覆盖范围内地形起伏相对平缓的情况,无法检测到局部陡峭地形对节点间信号传输的阻挡。因此,在后续研究中需要进一步探讨适用于陡峭地形的节点部署方法。