基于数据同化的气动压力稀疏重构方法

黄俊，郭雨欣，冀晶晶，黄永安

华中科技大学 机械科学与工程学院，武汉 430074

0 引言

风洞作为空气动力学研究的重要地面实验设备，在先进飞行器研制和基础空气动力学问题研究中发挥了不可替代的作用。实验流体力学（EFD）着眼于风洞实验数据的采集、分析和处理，是风洞系统工程中不可分割的部分。作为风洞技术测量目标之一，表面压力的测量直接关系到飞行器的升力系数与姿态控制，同时还可以通过压力分布判断飞行器表面的分离、转捩等信息。现有的压敏材料（PSP）利用非接触方式获得连续、大范围的模型表面压力分布[1]，是风洞实验中有效的测压方法，然而，基于光学原理的PSP 存在观测死角（如飞机短舱内表面）问题。传统的在模型表面布设测压孔的方法技术成熟度高、测量准确性好、可按需布置[2]，最新发展的柔性智能蒙皮可以粘贴于模型内外表面，实现多物理量同步测量[3-4]。但测压孔和柔性传感阵列往往数量有限，需发展基于稀疏测点的场重构技术，实现壁面绕流及空间流场的感知。

流场数据具有多维度且复杂的特点，而测量值来自壁面稀疏测点，如何构建有限数据与全空间流场的映射关系是流场重构的难点所在。国内外学者从流场物理模型与数据驱动的角度进行了理论尝试，Vamsi Krishna 等[5]基于快速畸变理论和Taylor假设建立双向加权模型，基于先验速度场对湍流演化进行重构。Callaham 等[6]探索了基于二维流场稀疏表示和数据库的流场重构法，尝试了数据驱动的流场重构技术，并讨论了需要的随机测点最小数量。Sun 等[7]结合Bayesian 神经网络与先验物理模型重构了二维钟形与T 形流场，并对结果不确定性进行估计。李静等[8]采用本征正交分解方法，以较少阶模态高精度再现非定常圆柱绕流的完整流场。这些重构方法大多局限在简单几何和稳态流场重构，与实际工程应用之间仍存在一定距离。得益于计算流体力学（CFD）的发展，通过数值方法求解Navier–Stokes 方程[9]，能够得到丰富的流场先验知识，为全流场重构提供良好的条件。然而，CFD 的计算过程通常不能充分考虑风洞实际流动过程中的不确定性[10]，导致确定性的计算机仿真难以复现风洞实验对物理参数的影响，从而无法实现与风洞实测数据的匹配和融合。因此，结合CFD 与实测稀疏数据对风洞的真实流场进行重构极富挑战。

数据同化（Data Assimilation，DA）方法能够结合估计值和测量值进行预测[11]，可以作为联系CFD理论先验信息和EFD 风洞实测数据的桥梁，其在流场重构中已有发展。Chandramouli 等[12]提出一种变分数据同化方法，通过圆柱绕流在过渡状态下的三维湍流尾流案例进行方案验证，与PIV 实验数据对比，验证了变分数据同化在不可压缩湍流重构中的有效性。Belligoli 等[13]通过数据同化方法实现了二维翼型的迎角及马赫数的修正，降低了实验测量值与RANS 模拟计算值之间的误差。集合变换卡尔曼滤波（Ensemble Transform Kalman Filter，ETKF）是卡尔曼滤波（Kalman Filter，KF）针对非线性系统模型的扩展方法[14]，在复杂系统中有良好的数据同化效果。ETKF 以蒙特卡洛方法为依托，以贝叶斯原理为核心，利用稀疏测量数据所包含的信息对物理场先验预报数据进行滤波，借此给出对不确定参数的连续后验估计[15]。该方法源自地球物理领域，是基于海面离散探测数据对海洋与大气的真实演化状态进行连续修正的重要工具[16]。近年来，国内外学者将该方法引入空气动力学领域，美国加州大学通过无限长薄板周围随机扰动无黏涡流模拟，印证了ETKF 在流场数据同化中的有效性[17]。日本宇航研究开发机构（JAXA）应用ETKF 对风洞中存在不确定性的马赫数、迎角、湍流黏度进行估计[18]，成功重构刚性机翼绕流场，证实了该方法对风洞中复杂流场的估计能力。国内上海交通大学在预测直升机转子三维流场特征时，采用了ETKF 优化剪切应力传输模型常数，为修正逆压梯度下边界层流动分离提供了参考[19]。

本文面向风洞实验的压力测量应用，使用集合变换卡尔曼滤波方法，以二维翼型RAE 2822 和二维对称翼型NACA 0012 为研究对象，进行机翼表面气动压力重构，以达到风洞实验对全域数据重构精度的要求。先通过CFD 计算得到全域先验分布，结合机翼表面有限数量的压力测量值，对机翼的迎角及马赫数进行修正，重构得到高精度的机翼周围全域压力场。再采用ETKF 进行流场数据同化：一方面，可以充分利用稀疏测量数据，将这些高精度数据泛化到整个流域，使得最终展示的流场更加接近真实的流场，为空间全域感知提供可能；另一方面，ETKF 可以作为一种流场风洞干扰的修正方法，基于真实测量数据，直接进行流场分布的修正，获取高精度的流场分布。

1 集合变换卡尔曼滤波方法

1.1 系统模型

在流场计算中，从边界条件到物理量的分布不是简单的线性系统，而是离散的非线性系统，其中状态变量估计可通过求解Navier–Stokes 方程得到。本文通过软件FLUENT 对流场进行数值计算，选用Spalart–Allmaras（S–A）湍流模型。采用Navier–Stokes 方程作为流动控制方程，并将此方程作为卡尔曼滤波中的系统模型：

式中：W 为守恒状态矢量，包含了密度、速度和能量；V 为控制体体积；Fc为对流通量；Fv为黏性通量；S 为控制体表面积；n 为控制体外法线方向的单位矢量；τ为时间。

1.2 状态空间矩阵

系统模型的估计与实验测量均存在误差，卡尔曼滤波的数据同化手段通过状态空间模型将误差代入系统当中：

式中：下标t 表示迭代次数，xt、yt向量分别表示系统模型和实验测量数据的状态向量，vt、ωt向量分别表示系统模型的噪声和观测噪声，假定其符合高斯分布。非线性算子F 是从第t-1次迭代到第t 次迭代的映射，在数据同化中，由系统模型计算得到。H矩阵是将系统估计的数据矩阵投影到实验观测数据的投影矩阵。

向量xt包含了迎角α、马赫数Ma 和所有（n 个）计算网格节点上的密度ρ、笛卡尔速度分量u、v 和压力p，其维数l=4n+2，向量xt的表达式为：

向量yt由实验测点对应位置的测量值构成。在稀疏压力重构中，选取实测压力p，向量yt维数与实验测点的数量（m 个）一致：

1.3 集合变换卡尔曼滤波方法及实现流程

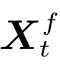
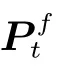
式中：H为式（3）中的投影矩阵，在翼型网格和实验模型的对应位置设置为1，其余位置设置为0。

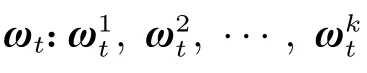
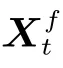
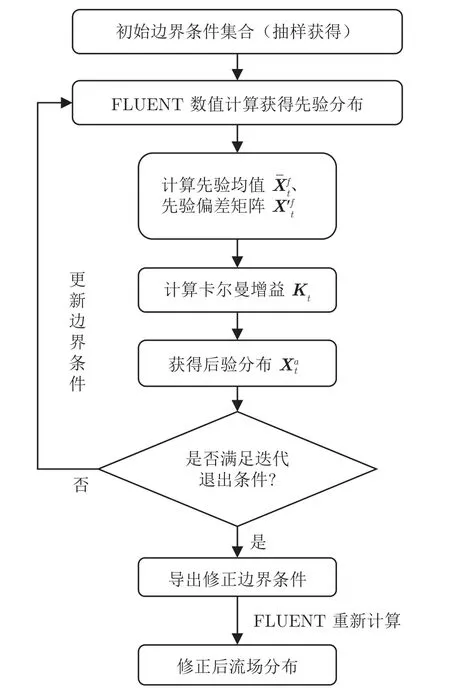
图1 ETKF 流程图Fig.1 The flowchart of ETKF

在各物理量符合收敛条件判定准则之后，将最后一次迭代的集合元素均值作为整个数据同化过程的来流条件修正值，代入FLUENT 进行重新计算，得到修正后的流场分布。

2 实验过程和结果

RAE 2822 是一个二维跨声速湍流流动的经典翼型，被许多国外的项目合作组（如EUROVAL）选作经典算例[21]；NACA 0012 作为经典的对称翼型，有实验数据可用来验证其数值模拟的准确性，故本文实验使用二维翼型RAE 2822 和NACA 0012 进行验证。RAE 2822 翼型实验主要用来展现重构的收敛过程，ETKF 对迎角、马赫数的影响，以及与其他方法在精度上的对比；NACA 0012 翼型实验则面向风洞测量中基于有限测点重构的需求，用以探究影响ETKF 重构精度的因素。

2.1 RAE 2822 翼型压力重构

2.1.1 网格和计算条件设置

使用ICEM 软件对RAE 2822 进行网格划分（图2），采用四边形结构化网格，机翼模型弦长c=1 m，计算域在弦长方向（即x 方向）为40 m，弦长垂直方向（即y 方向）为40 m，网格质量如表1所示。本文笛卡尔坐标系的原点位于机翼最前缘点。将FLUENT 软件的计算模型设置为S–A 湍流模型，此模型对跨声速流动的求解有较好的效果，且计算成本相对较低。自由流空气设置为可压缩空气，计算方式为稳态计算。实验数据来源为Cook 等[22]的案例6 中RAE 2822 跨声速实验压力数据，其实验工况为：Ma=0.725，α=2.92°，Re=6.2×106。共有103 个测量点，其中一部分测点与机翼网格点难以匹配，会给数据同化带来较大误差，将其去除后剩余的压力测点个数为75（即m=75）。

表1 RAE 2822 网格质量及节点数量Table 1 Quality and node number of RAE 2822 mesh

图2 RAE 2822 翼型网格Fig.2 Mesh of RAE 2822 airfoil

2.1.2 RAE 2822 翼型ETKF 数据同化结果

2.1.2.1 迎角及马赫数

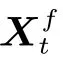
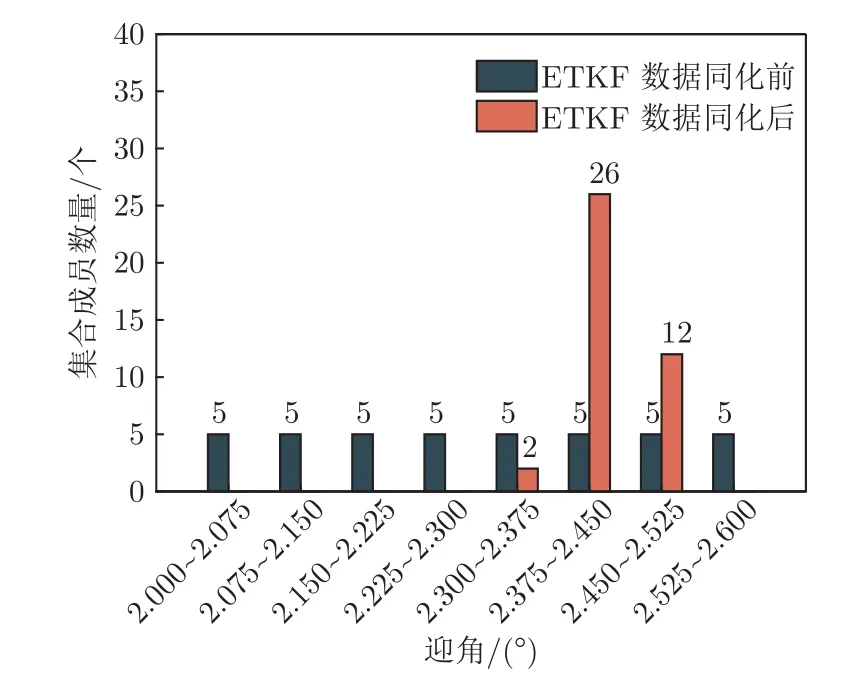
图3 集合成员迎角在ETKF 同化前后的分布Fig.3 Distribution of ensemble angel of attack before and after ETKF assimilation

图4 集合成员马赫数在ETKF 前后的分布Fig.4 Distribution of ensemble Mach number before and after ETKF assimilation

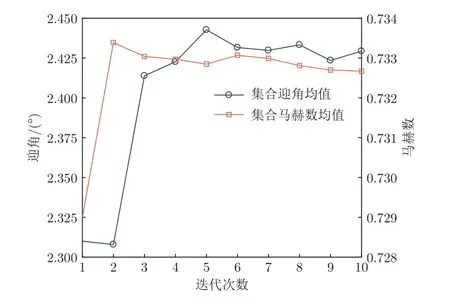
图5 集合的迎角及马赫数均值随迭代过程的变化Fig.5 Mean of angle of attack and Mach number changes with iterations

图6 为迭代过程中所有网格点的密度（ρ）、速度分量（u、v）和压力系数（Cp）的均方误差MSE 变化曲线。从图中可以看出，在进行了第3 次迭代之后，所有物理量的均方误差已经小于第一次迭代的1%，这表明在第3 次迭代时ETKF 就已经满足收敛要求，继续迭代发现均方误差可以进一步降低，于是迭代继续进行。

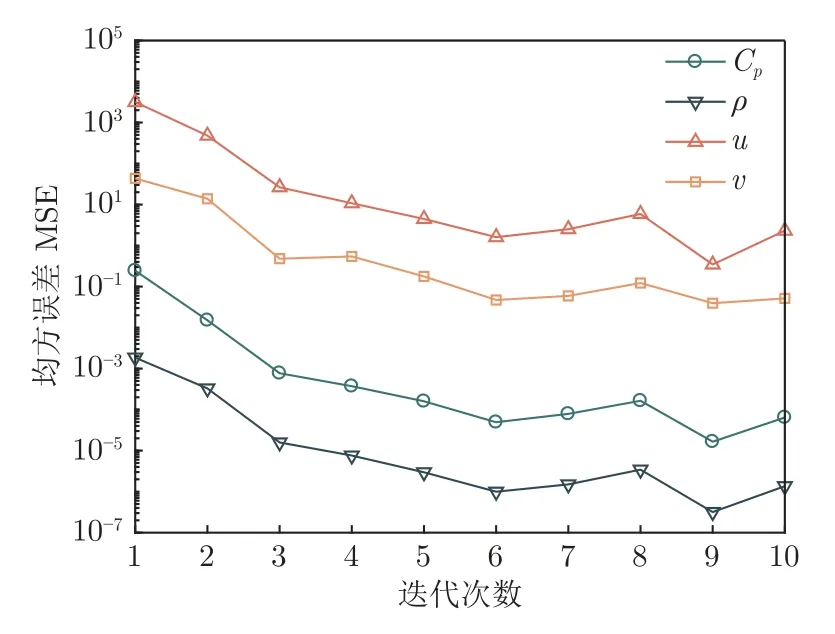
图6 ρ、u、v、Cp 的MSE 随迭代过程的变化Fig.6 MSE of ρ,u,v and Cp changes with iterations

随着迭代的进行，集合中所有成员的边界条件都在产生变化并且更加集中（图3 和4）。计算集合成员的方差如表2所示，可以看到在数据同化过程中，随机抽样产生的所有集合成员在向更为准确的修正值变化，且马赫数的集中效果要比迎角的集中效果更好。最终，集合成员迎角及马赫数均值在第10 次迭代之后分别收敛为2.434°和0.732 8（图5）。

表2 ETKF 前后集合成员迎角、马赫数的均值及方差Table 2 Mean and variance of ensemble angle of attack and Mach number before and after ETKF

2.1.2.2 压力系数、升力系数和力矩系数

基于图2 网格，将收敛后集合成员的迎角及马赫数均值（表3）作为边界条件代入FLUENT 进行重新计算，得到ETKF 同化后的压力系数Cp曲线分布，此结果即为ETKF 数据同化的最终结果。将ETKF 同化结果与线性理论修正值进行对比，结果如图7 和8所示。

表3 RAE 2822 case 6 边界条件Table 3 Boundary condition of RAE 2822 case 6

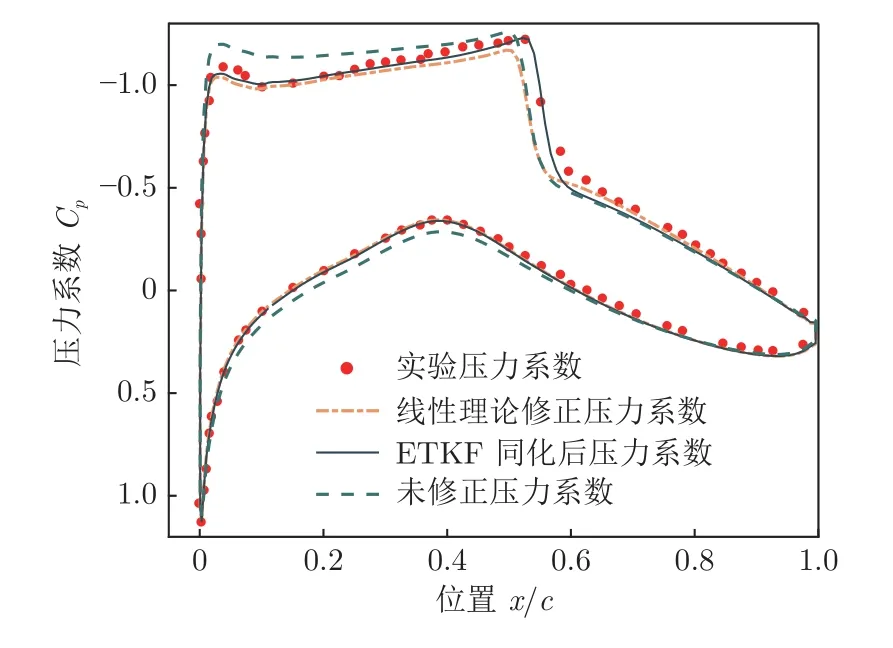
图7 ETKF 同化后的压力系数曲线与线性理论修正曲线对比Fig.7 Comparison of the pressure coefficient curve after assimilation of ETKF with the linear theory correction

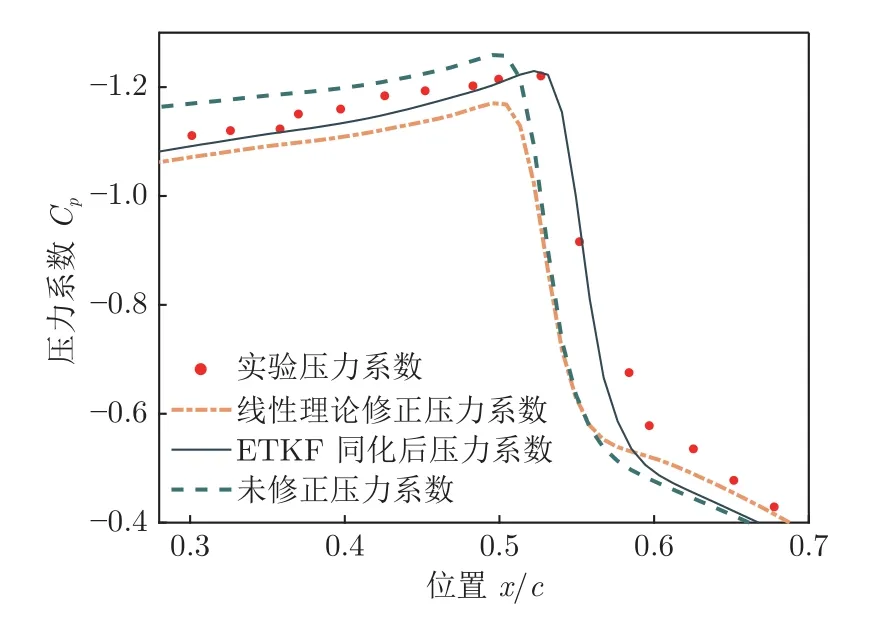
图8 激波位置的压力系数对比Fig.8 Comparison of pressure coefficient at shock position

从图7 和8 中可以看出：与线性理论修正后的计算结果相比，ETKF 同化后的压力系数曲线更加靠近实验数据；线性理论的迎角修正值过大，导致其计算误差与ETKF 相比更大，尤其是在激波位置。从数值上分析（式（25））可得，ETKF 同化的压力系数平均相对误差e 比线性理论修正后降低了约3%。e 的计算方法如下：

式中：j 为实验测点的数量，Cp,exp为实验测点的压力系数。

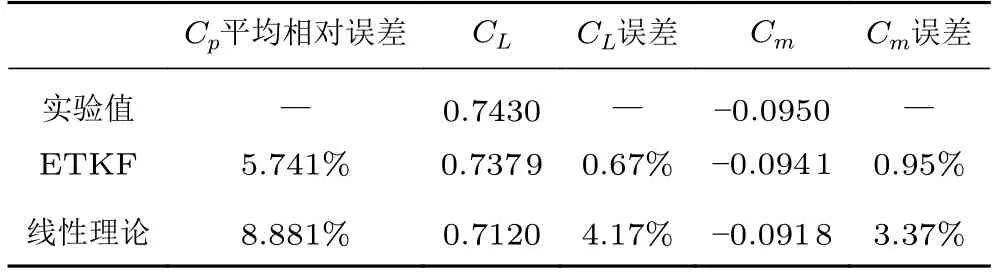
表4 ETKF 同化和线性理论修正后CL 和Cm、激波位置Cp 平均相对误差与实验值的对比Table 4 Comparison of CL,Cm and Cp average relative error near the shock wave position between ETKF,linear theory and experiment

2.2 NACA 0012 翼型压力重构

2.2.1 网格和计算条件设置

如图9 和表5所示，NACA 0012 翼型采用的计算网格为四边形结构化网格，机翼模型弦长c=0.152 4 m，计算域在弦长方向为4.5 m，在垂直弦长方向为5 m，网格质量高，FLUENT 计算时选用S–A湍流模型。实验数据来源于NASA 进行的NACA 0012 翼型风洞实验[23]，选取TEST 119 的压力数据进行数据同化的测试，其实验工况为：Ma=0.402 2，α=4.020 8°，Re=6.070 6×106。共有46 个压力测量点，由于靠近机翼前缘位置的数据在同化时难以与网格节点进行匹配，容易带来较大误差，故在同化时将其去除，仅使用其中44 个数据（即m≤44）。

表5 NACA0012 网格质量及节点数量Table 5 Quality and node number of NACA 0012 mesh

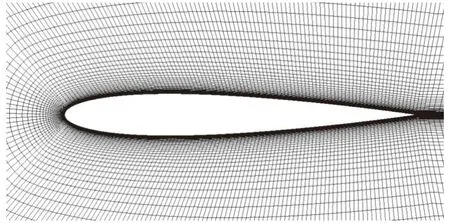
图9 NACA 0012 翼型网格Fig.9 Mesh of NACA 0012 airfoil

NACA 0012 翼型实验主要面向风洞测量中基于有限测点重构的应用需求，对比分析基于少数测点进行压力稀疏重构的可行性。图10 给出了实验压力测点的位置及序号。实验共进行4 组，其中3 组实验分别选用上翼面（序号1～22）的不同位置6 个实验测点进行数据同化，第4 组实验作为同化结果的对标，使用所有数据测点进行同化处理。

图10 NACA 0012 实验测点位置及序号Fig.10 Test point location and serial number of NACA 0012

2.2.2 NACA 0012 翼型ETKF 数据同化结果

在数据同化之前进行初始集合的抽样，因为此实验无具体参考修正值，故基于实验原始工况进行初始值的抽样，并设定较大的抽样范围。设置集合成员数量k=40，在3.52～4.52 范围进行迎角抽样，在0.372 2～0.432 2 范围进行马赫数抽样，得到初始集合的迎角均值为4.020 8°，马赫数均值为0.402 1。采用第1 节的理论与流程进行数据同化，同化实验1～4 均从此初始值开始分别进行迭代，以对比使用不同实验测量数据得到的迭代效果。4 组实验所用的压力测点及迭代至收敛所需的迭代次数见表6。

表6 4 组实验的压力测点序号及迭代次数Table 6 The number of pressure measuring points and iteration times of 4 groups of experiments

实验结果如表7 和图11所示，表7 中压力系数平均相对误差由式（25）计算得到，4 组同化实验均使用上翼面实验测量值进行误差的计算（即j=22）。如图11所示，相比于深绿色点划线表示的未同化实验数据，经过ETKF 同化的压力系数均有一定的优化效果。同化实验4 使用了所有实验测量点进行同化，其结果的误差最小，只有1.05%，说明ETKF 方法的同化精度与使用的数据量有关，测点数据越多，得到的同化效果越好；只采用6 个测点进行同化的实验1～3 也达到了小于6%的平均相对误差，证实了基于有限测点进行压力稀疏重构、实现全域感知的可行性。且对比同化实验1～3 的结果可以发现，重构精度与初始测点位置的选取密切相关，初始测点位置不同，相对误差从2.42%到5.74%不尽相同，这说明在风洞实验时可以基于重构算法进行传感测点位置的优化布置。

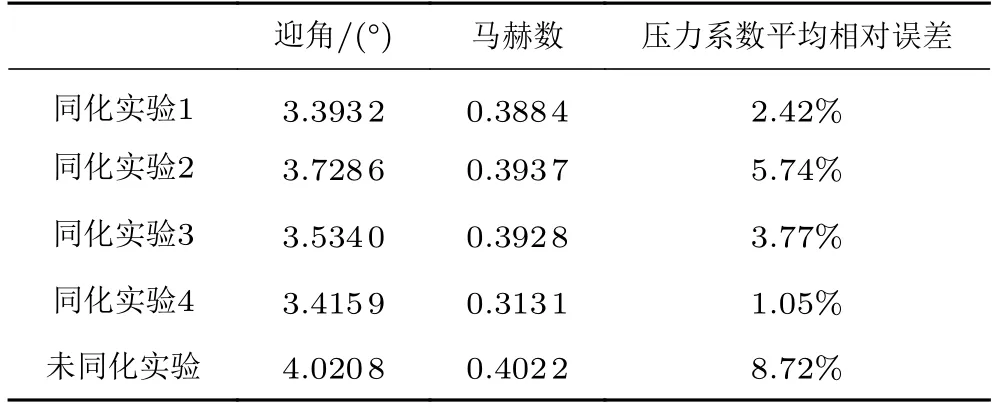
表7 4 组实验ETKF 后的迎角、马赫数及压力系数平均相对误差Table 7 Angle of attack,Mach number and pressure coefficient average relative error after ETKF in 4 groups of experiments

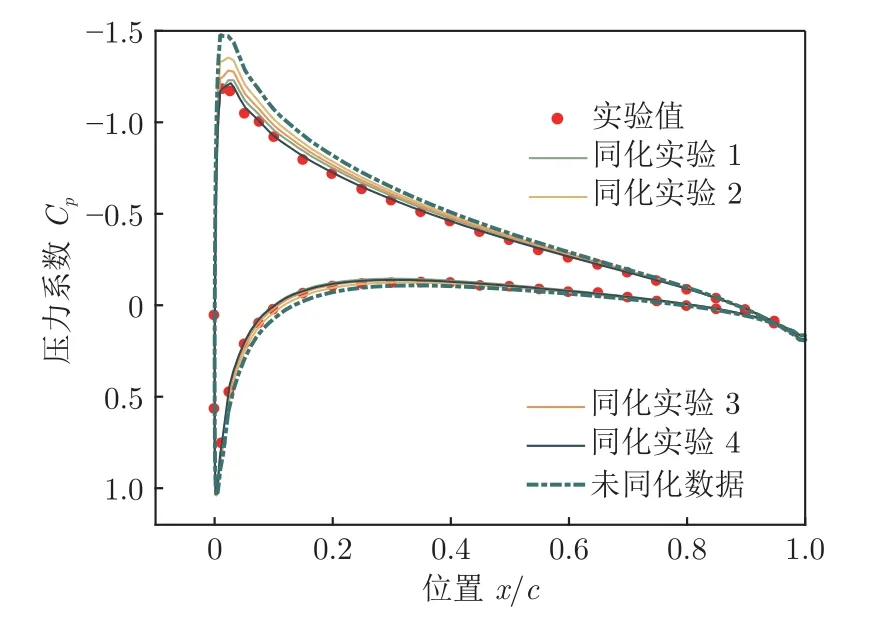
图11 NACA 0012 的ETKF 同化结果与实验值的对比Fig.11 Comparison of ETKF assimilation results with experimental values in NACA 0012

3 结论

本文针对风洞测量中有限测点进行气动压力重构开展研究，使用集合变换卡尔曼滤波方法对二维翼型RAE 2822 和NACA 0012 的湍流流场进行数据同化，结合稀疏的实验测量压力数据，对两种翼型的实验迎角及马赫数进行修正，通过修正后的边界条件进行重新计算得到了全域流场。将ETKF 同化后的机翼表面压力系数及机翼的升力系数、力矩系数与修正前数据和线性理论修正值作对比，得到以下结论：

1）ETKF 可以通过有限的测量信息进行流场的全域重构，其重构的精度与测量点的选取有直接关系，在实验测量位置进行压力系数的修正，其精度比经典线性理论更加靠近实验测量值。

2）使用ETKF 修正后的迎角及马赫数计算得到的机翼升力系数及力矩系数与实验测量值之间的误差很小，这表明了基于ETKF 数据同化的有效性。

3）由于ETKF 进行同化的数据基础是实验测量数据，其对于流场的估计精度取决于此测量值的准确性。

本文研究表明，作为一种用于湍流流场的数据同化方法，集合变换卡尔曼滤波能够有效利用CFD数值计算数据和EFD 高精度稀疏测量数据，重构得到更高精度的全域流场，适用于湍流场稳态计算的分布预测。本文在给定了实验迎角及马赫数的条件下进行了压力场稀疏重构，后续可以进一步进行其他分布条件下（如剪应力分布）的数据同化实验，进行多数据融合下的流场重构，推进风洞实验测量技术向高效化发展。