考虑需求侧响应的多能互补微电网优化调度研究
尚文强,丁月明,季金豹,谭亲跃,庞博文,康定毅
(1.西北农林科技大学 水利与建筑工程学院,陕西 咸阳 712100;2.国网山东省电力公司日照供电公司,山东 日照 276800)
随着“双碳”战略目标的实施,以高比例新能源渗透为特点的新型电力系统正在构建[1-2],目前风光等新能源的发电占比也在不断提高,具有能源梯级利用、多能耦合互补等优点的多能互补微电网是电力系统逐步转型向新的关键途径[3-4]。然而,由于电网自身协调性能有限而且国内电力市场机制尚待完善,导致新能源出力的随机性、间歇性带来的影响等问题随着其渗透率的不断提高而日益突出[5]。
关于多能互补微电网不确定性方面的研究,文献[6]假设电、气和热三种能源之间形式上的差异,以热力学第一定律为基础的综合能效利用率为指标对能源互联网的配置进行优化,同时注重了生产转换过程中能量的数量变化。文献[7]研究了含有电动汽车的需求侧其充电放电行为随电价激励水平改变的规律,对电动汽车充放电行为的不确定性进行建模。文献[8]考虑了传统新能源发电与负荷的不确定性,建立了多能互补微电网多目标日前调度优化模型。文献[9]考虑了精细化多能互补微电网中多能负荷的不确定性建模,提高了多能互补微电网调度的鲁棒性。文献[10]研究了电气能源互联网中新能源发电的高阶不确定性,通过分布鲁棒优化模型对调度成本进行优化。
针对需求响应在微电网中的研究,文献[11]研究了热电耦合系统,通过弹性需求侧响应引导客户用电,发现可以提高微电网的光电消纳能力和经济效益。文献[12]通过优化多种需求负荷的分时电价,提高园区新能源的消纳率。文献[13]对孤岛型微网新能源和储能的容量优化方法和分时电价进行了建模,对荷侧的电价进行优化以促进新能源消纳。文献[14]对用户侧的分时电价进行优化,以系统内电负荷与新能源发电量的差值最小为决策目标,考虑的影响因素较少。文献[15]建立了综合能源系统内负荷代理商与系统运营商的博弈模型对电价进行优化,对系统内多种能源进行定价从而提高风电消纳率。
基于上述研究基础,本文提出一种调度优化方法,构建能源管理模型。因此,能源管理模型采用本文提出的随机-鲁棒优化模型求解多重不确定条件下系统源网荷储的协同调度。最后,本文对多能互补微电网优化调度结果进行分析,验证了本文所建模型和求解算法的有效性。
1 微电网能源管理优化模型
考虑到多能互补微电网电力生产与负荷需求两侧所体现出的不确定性,采用随机优化中的场景分析方法先处理负荷的不确定性,进而采用两阶段鲁棒优化方法处理传统风光出力的不确定性,以实现系统的源网荷储协同调度。
能源管理模型中,首先,随机优化依据概率分布抽取场景,然后对每个负荷场景分别求解两阶段鲁棒优化调度问题,以最小化各负荷场景下成本的加权平均值为优化目标;决策变量为电、热、气网各设备运行状态及出力、弃风和弃光功率、由配电网和天然气网络输送的功率;约束条件为功率平衡约束、各设备运行约束、购电购气约束等。采用强对偶理论和列和约束生成算法(column-and-constraint generation, 简称C&CG)求解。
本文对集电、热、气负荷于一体的多能互补微电网进行了建模。系统中电负荷由热电联产机组(combined heat and power, 简称CHP)、燃料电池、风力发电机、光伏发电系统、锂电池储能设备和配电网供给,气负荷由电转气设备(power to gas, 简称P2G)、储气罐和天然气网络供给,热负荷由电热锅炉、燃气锅炉和余热回收装置供给。能源耦合设备主要包括 P2G、CHP、燃料电池、电热锅炉和燃气锅炉,其中 P2G 是电、气、热子系统的关键能源耦合设备。多能互补微电网从多种能源总体规划的角度实现了多种能源系统的耦合。具体能量耦合关系如图1所示。
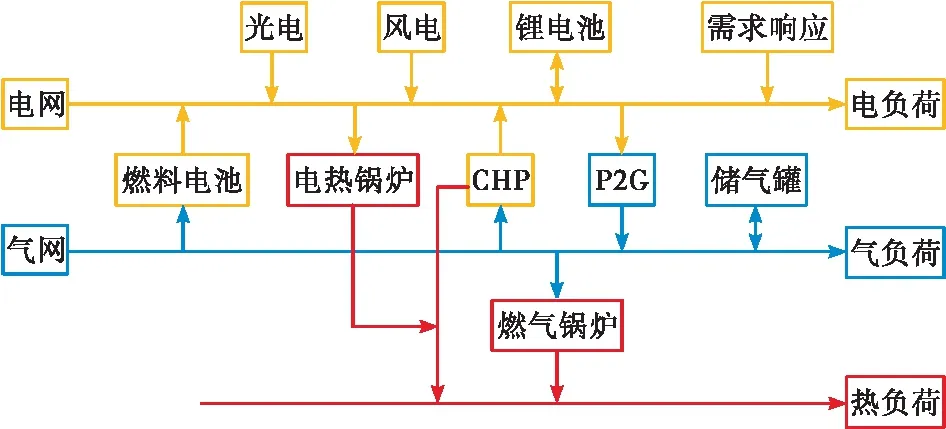
图1 多能互补微电网能流图
2 计及多重不确定性的能源管理模型
本文结合源荷两侧的不确定性,首先,采用随机优化中的场景分析方法来处理负荷的不确定性,进而,采用两阶段鲁棒优化方法处理传统风光出力的不确定性;最后,通过最小化各机组的启停成本与购电购气成本提升多能互补微电网的经济效益。
2.1 两阶段鲁棒优化模型
本文搭建的两阶段鲁棒优化模型的目的在于找到不确定变量u在不确定集U内朝着最恶劣场景变化时经济性最优的调度方案,模型的可行解是当模型参数在不确定集合中任意取值时,能够保证所有约束均满足的一组确定的数值解,本文搭建的模型具有如下形式:
(1)
其中:
(2)
不确定集U具有如下形式:
(3)
其中:
(4)
式中:Re,grid(t)和Rg,net(t)分别为t时段系统向天然气网络购气成本和向配电网购电成本,元;Ri,su(t)和Ri,sd(t)分别为t时段系统内各机组的开机成本和关机成本,元;ui(t)为t时段系统内第i台机组启停状态,为0/1变量;Pe,grid为t时段系统购电功率,kW;Gg,net为t时段系统购气功率,kW;ri,su和ri,sd分别为t时段系统内第i台机组的单次开机费用和单次关机费用,元;re,grid(t)和rg,net(t)分别为t时段系统向配电网购电价格和向天然气网络购气单价,元;PWT(t)、PPV(t)和PDR(t)分别为t时段风光出力实际功率和负荷实际响应量,kW;Pf,WT(t)、Pf,PV(t)和Pf,DR(t)分别为t时段风光出力预测功率和负荷预测响应量,kW;ΔPWT(t)、ΔPPV(t)和ΔPDR(t)分别为t时段风光出力预测误差和负荷响应预测误差,kW;z(t)为二进制变量,取值为1时相应时段的不确定变量即取到区间的边界。
在 min-max-min 函数中,max 函数是求解不确定集U的最恶劣场景,一、二阶段 min 函数是求解使多能互补微电网中机组启停成本和能源调度成本最小的调度方案,第一阶段 min 为最小化机组启动和关闭成本,第二阶段 min 是在最恶劣场景下最小化购买天然气和交流电的成本。此外,本文考虑了不确定变量的“不确定性调节参数”Γ,表示系统在调度周期内不确定变量取到不确定集U所描述的波动区间的最大值或者最小值的时段总数,用以调节调度方案的经济性和鲁棒性。
2.2 随机-鲁棒优化模型
随机优化的思想是为不确定的变量构建或采样可能出现的场景,求解每一个可能出现的场景的确定性问题,并以结果的加权组合来表示随机性问题的解。
(5)
式中:Ps为各场景发生的概率;S(xs,us,ys)为系统在s场景下的成本函数。
本文采用随机优化中的场景分析技术处理负荷预测不确定性,依据概率分布使用拉丁超立方抽样技术抽取负荷场景,对每个负荷场景分别求解两阶段鲁棒优化调度问题,以最小化各负荷场景下机组启停成本和能源调度成本之和的加权平均值为决策目标。本文提出的随机-鲁棒优化调度问题定义如下:
(6)
针对由负荷概率分布随机生成的诸多场景,场景数量过多会导致求解问题变得复杂,场景数量过少又会影响调度结果的精确性,因此本文采用场景缩减技术 K-means 聚类法将负荷场景缩减,得到其近似子集。
2.3 多能互补微电网各设备数学建模及约束条件
1)天然气子系统气量平衡约束
GP2G,s(t)+Gg,s(t)+GGS,dis,s(t)-GGS,ch,s(t)=
GCHP(t)+GFC(t)+GGB(t)+GL(t)
(7)
式中:GP2G,s(t)为t时段s场景下 P2G 设备产气功率,m3;GGS,ch,s(t)和GGS,dis,s(t)分别为t时段s场景下储气罐充放气功率,m3;GCHP(t)、GFC(t)和GGB(t)分别为t时段s场景下 CHP 设备、燃料电池和燃气锅炉耗气功率,m3;GL(t)为t时段s场景下气负荷,m3。
2)电力子系统交直流功率平衡约束
(8)
式中:PCHP,s(t)、PFC,s(t)、PFC,s(t)和PPV,s(t)分别为t时段s场景下 CHP 设备、燃料电池、风力发电机和光伏电池发电功率,kW;PES,ch,s和PES,dis,s分别为t时段s场景下锂电池充放电功率,kW;PP2G,s(t)和PEB,s(t)分别为t时段s场景下 P2G 设备和电热锅炉耗电功率,kW;PWT,cut,s(t)和PPV,cut,s(t)分别为t时段s场景下弃风弃光功率,kW。
3)热力子系统热量平衡约束
HCHP,s(t)+HEB,s(t)+HGB,s(t)=HL,s(t)
(9)
式中:HCHP,s(t)、HEB,s(t)和HGB,s(t)分别为t时段s场景下 CHP 设备、电热锅炉和燃气锅炉产热功率,kJ;HL,s(t)为t时段s场景下热负荷,kJ。
4)CHP 设备模型及约束
CHP 设备、余热回收装置的数学模型、运行约束、爬坡约束和开关机最小时间约束如下所示:
(10)
(11)
HHR,s(t)=HCHP,s(t)ηHR
(12)
uCHP,s(t)PCHP,min≤PCHP,s(t)≤uCHP,s(t)PCHP,max
(13)
-rCHP≤PCHP,s(t)-PCHP,s(t-1)≤rCHP
(14)
(15)
(16)
uCHP,s(t)∈{0,1}
(17)
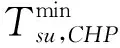
5)燃料电池模型及约束
燃料电池的数学模型、运行约束如下所示:
(18)
uFC,s(t)GFC,min≤GFC,s(t)≤uFC,s(t)GFC,max
(19)
uFC,s(t)∈{0,1}
(20)
式中:uFC,s(t)为t时段s场景下燃料电池启停状态;ηFC、GFC,max和GFC,min分别为燃料电池产电效率和运行功率上下限。
6)P2G 设备模型及约束
P2G 设备的数学模型、运行约束如下所示:
(21)
uP2G,s(t)PP2G,min≤PP2G,s(t)≤uP2G,s(t)PP2G,max
(22)
uP2G,s(t)∈{0,1}
(23)
式中:uP2G,s(t)为t时段s场景下 P2G 设备启停状态;ηP2G、PP2G,max和PP2G,min分别为P2G设备产气效率和运行功率上下限。
7)锂电池模型及约束
锂电池的数学模型、荷电状态约束和运行约束如下所示:
(24)
SOCs(t)=WES,s(t)/WES
(25)
SOCmin≤SOCs(t)≤SOCmax
(26)
SOC(0)=SOC(24)
(27)
(28)
(29)

8)储气罐模型及约束
储气罐的数学模型、容量约束和运行约束如下所示:
(30)
(31)
WGS(1)=WGS(24)
(32)
(33)
(34)
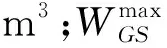
9)电热锅炉模型及约束
电热锅炉的数学模型和运行约束如下所示:
HEB,s(t)=PEB,s(t)ηEB
(35)
uEB,s(t)PEB,min≤PEB,s(t)≤uEB,s(t)PEB,max
(36)
uEB,s(t)∈{0,1}
(37)
式中:uEB,s(t)为t时段s场景下电热锅炉启停状态;ηEB、PEG,max和PEB,min分别为电热锅炉产热效率和运行功率上下限。
10)燃气锅炉模型及约束
燃气锅炉的数学模型和运行约束如下所示:
(38)
uGB,s(t)GGB,min≤GGB,s(t)≤uGB,s(t)GGB,max
(39)
uGB,s(t)∈{0,1}
(40)
式中:uGB,s(t)为t时段s场景下燃气锅炉启停状态;ηGB、GGB,max和GGB,min分别为燃气锅炉产热效率和运行功率上下限。
11)配电网与天然气网络功率约束
(41)
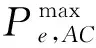
12)弃风弃光功率约束
(42)
3 多能互补微电网优化模型求解
针对模型中的两阶段鲁棒优化模型,本文采用列和约束生成算法(C&CG),将原问题式(1)分解为主问题式(43)和子问题式(44)进行交替求解,以此得到原问题的最优解。分解得到的主问题形式为
(43)
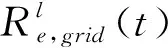
经分解后的子问题形式为
(44)
在给定的(x,u)下,式(51)的内层最小化是一个线性问题,根据线性优化中的强对偶理论,可将内层 min 转化为 max 形式,并与外层的 max 问题合并。
将主问题和子问题中存在的非线性项线性化,两阶段鲁棒优化模型最终解耦为混合整数线性规划问题,随后可用 C&CG 算法进行求解。
4 算例分析
4.1 参数设置
本文以山东某多能互补微电网为研究对象,原始电、气、热负荷曲线如图2所示,预测风电、光伏出力曲线如图3所示,可以看出,1d内光伏发电主要集中在中午11∶00—15∶00,风力发电凌晨04∶00达到最高峰,交流负荷高峰时段处于早08∶00—12∶00和晚16∶00—21∶00。设电、热、气负荷概率分布是以预测值为均值,0.05倍均值为标准差的正态分布,首先采用拉丁超立方抽样随机生成电、气、热负荷各1 000个场景,然后采用K-means聚类法对原负荷场景进行缩减。多能互补微电网设备参数如表1所示,向配电网购电的分时电价如图4所示,向天然气网络购气的价格为0.35元/(kW·h)。
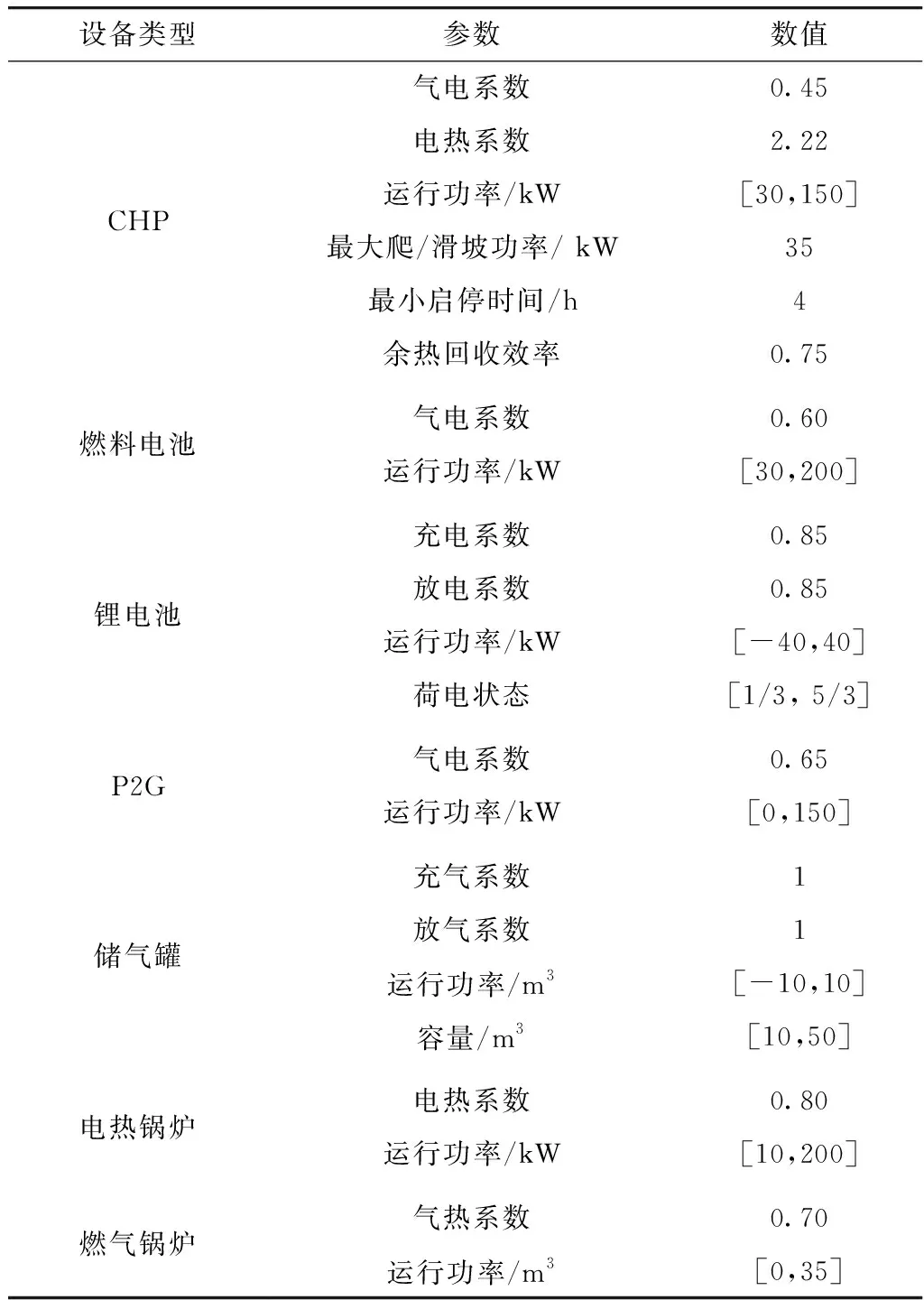
表1 多能互补微电网设备参数

图2 原始电、气、热负荷曲线
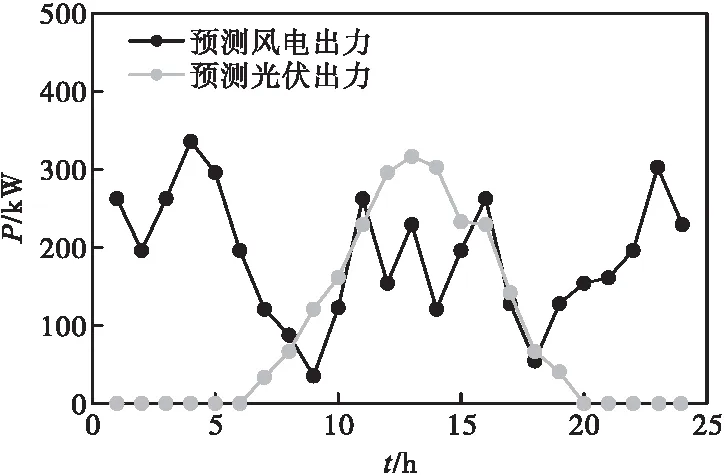
图3 预测风电、光伏出力曲线
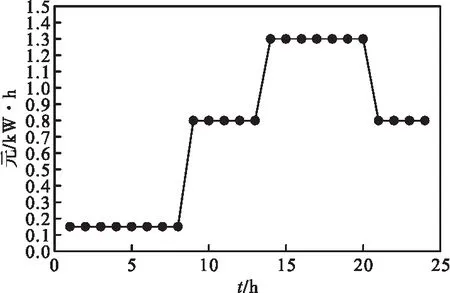
图4 配电网分时电价
4.2 多能互补微电网优化结果及分析
当光伏不确定性参数ΓPV取值为12,风电不确定性参数ΓWT取值为24时,电、气、热功率优化调度结果分别如图5~图7所示。图5~图7中,锂电池充放电功率大于0表示锂电池放电,小于0表示锂电池充电,储气罐同理。

图5 电力子系统协同调度结果
从图5电力子系统协同调度结果可以看出:在00∶00—06∶00、11∶00—16∶00时段,系统分别处于风力发电和光伏发电高峰时段,此时交流负荷较小,主要由新能源发电供应;在06∶00—09∶00时段,风光出力不足以供应交流负荷时,不足的电量向配电网购买;在06∶00—11∶00、19∶00—21∶00时段,系统电负荷处于高峰时段和新能源发电低谷时段,电负荷主要由购电功率和耗气机组购气出力供应。
从图6天然气子系统协同调度结果可以看出:气负荷主要由系统向天然气网络购气供应,只有在00∶00—09∶00时段部分由P2G设备供应;储气罐通过系统购气进行充气,必要时供应CHP、燃料电池及气负荷。
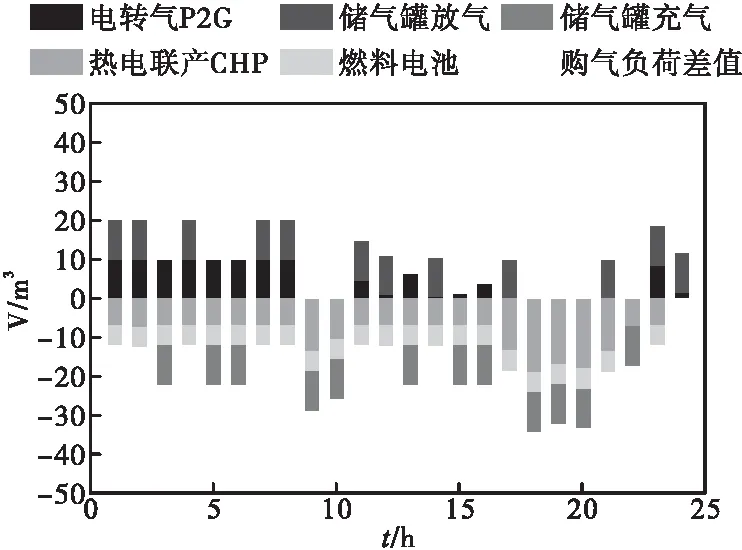
图6 天然气子系统协同调度结果
图7所示热力子系统协同调度结果中,CHP运行方式为“以热定电”模式,CHP的交流出力以设备在该时刻的热出力决定,当CHP不足以供应热负荷时,不足的热量由电热锅炉进行补充;由于CHP可以将气能转换为电能和热能,能量利用效率较高,故基本全日运作以提高系统经济性。

图7 热力子系统协同调度结果
4.3 新能源出力不确定性参数对调度结果的影响分析
选取三组新能源出力不确定性调节参数进行对比,参数设置及相应的调度成本如表2所示。

表2 不同不确定性调节参数对各类成本的影响
由表2可以看出,随着不确定性调节参数取值逐步增大,系统调度方案的鲁棒性就越强,调度方案就越加保守,具体体现在其运行成本的不断增大,系统所受到的经济性损失也不断增大。除此之外,可以看出系统购气成本随不确定性调节参数增大的增幅相比于系统购电成本的增幅更大,这是因为新能源出力不确定性增大,其产生的系统电功率缺额需通过系统直接向配电网购电或向天然气网购气由CHP机组和燃料电池发电弥补,而天然气发电的单位发电成本较配电网单位电价低,造成购气成本的增幅更显著。
5 结 语
本文研究了多能互补微电网在多重不确定性条件下源网荷储的协同调度的问题,建立了系统能量管理优化模型。结合山东某多能互补微电网进行仿真,对调度结果的分析表明:通过对所提出优化模型的求解,能够得到多能互补微电网在源侧风光出力不确定性、荷侧负荷预测不确定性条件下系统运行成本最小的协同调度方案;最后通过改变调节参数Γ,可以灵活调整系统调度方案的保守性,使系统决策在经济性和鲁棒性间进行合理选择。

