老油田集输管网布局优化技术研究
史海笑(大庆油田有限责任公司第六采油厂)
集输管网负责将井口采出液收集、处理并输送至中央处理厂。受地形地貌、油品物性和井组布局的影响,集输管网通常较为复杂,其投资在油气田地面工程的占60%~70%[1]。因此,对集输管网的布局进行优化研究,不仅可减少建设成本投资,还可降低运行能耗和风险隐患[2-3]。目前,我国大部分油田的开发已进入中后期,油井含水率和注水压力逐年上升,计量站和阀室的利用率下降。对于这种情况,通常是在原区块的基础上增加加密井和阀室,将其并入原集输管网,此时加密井的位置选择及布局方式显得尤为重要。
考虑管网中的温度、压力、流量等均为连续数据,管径和布局方式为离散数据,在确定井口位置后还需确定接入系统的最短路径,其求解难度随着井口数量的增加呈指数增长,该问题已被证明属于NP 难问题。王博弘等[4]在三维地形的约束下,对环枝状的集输管网进行了优化,总费用下降了7.06%;李俐莹[5]在综合考虑地理条件、环境信息和气候因素的条件下,实现了管网、井组及选址的优化;周金勇等[6]利用免疫遗传算法对环状集输管网进行了优化,确定了当集输半径为2 km 时,工程造价最低。以上研究均提出了具体算法和求解步骤,对不同节点间的连接关系和管道参数进行了核算,但均针对新建集输管网,对于老油田滚动开发中加密井和阀室的优化涉及较少。基于此,以总投资费用最小为目标函数,在考虑压力约束、管径集合约束、连头数量约束和隶属关系约束的前提下,通过分支定界法对目标函数迭代求解,并进行实际案例的验证和分析。
1 集输管网结构特点
目前,油田常用的管网结构有枝状、放射状和环状[7]。枝状管网有一条干线和数条支线,适合油井分散、面积狭长的油藏,虽然经济上较优,但在可靠性上存在弊端,一旦发生局部故障将影响整个管网。放射状管网又叫星状管网[8],由多条集油干线组成,在干线上某一点呈放射状连接至其他井口,适合油井较多、面积较大的油藏,虽然建设成本较高,但可靠性较好。环状管网是一条干线呈环状,油井顺着环依次接入干线,适合固定形状的油藏,具有调度方面、压力稳定的特点,适合油井固定的老油区改造,对于新建的加密井和阀组,由于其集输半径和管径受环管径的限制,故很难进行扩充。综上,为了减少对已有管网的冲击和影响,研究的老油田集输管网滚动布局优化是在枝状-放射状的管网基础上完成的[9]。
2 老油田集输管网布局优化模型
2.1 目标函数
优化模型的目标函数有管道长度最短、投资费用最少和运行费用最少等[10-11],考虑到新接入油井涉及管道和阀组费用,故采用投资费用最少作为目标函数。见式(1):
式中:F为总投资费用,元;i和k均为油井编号;j为阀组编号;xij为油井i到阀组j的连接关系,xij=1 表示相连,xij=0 表示不相连;yij为油井i到阀组j之间是否存在原有管道,yij=1 表示存在原有管道,yij=0 表示不存在原有管道;xik表示油井i到油井k的连接关系,xik=1 表示相连,xik=0表示不相连;yik表示油井i到油井k之间是否存在原有管道,yik=1 表示存在原有管道,yik=0 表示不存在原有管道;lij表示油井i到阀组j的长度,m;lik表示油井i到油井k的长度,m;Aij表示油井i到阀组j的管道单位长度价格,元/m;Aik表示油井i到油井k的管道单位长度价格,元/m;uj为状态变量,uj=1 表示新建阀组存在,uj=0 表示新建阀组不存在;Bj为一个阀组的价格,元/个。
2.2 约束条件
1)压力约束。油井进阀组的压力,不应小于最小允许进阀组压力,见式(2):
式中:pij为油井i到阀组j的压降,MPa;pi为油井i的井口压力,MPa;pj为阀组j的最小允许压力,MPa。
2)连头数量约束。鉴于阀组的连头数量在投产初期有所固化,故要考虑该约束对优化的影响,见式(3):
式中:Mmax为连头最大数。
3)隶属关系约束。每个油井只能与一个阀组或其余油井相连,见式(4):
4)管径集合约束。管径应在可供选择的范围内,见式(5):
式中:Dij为油井i到阀组j的管径,mm;Dik为油井i到油井k的管径,mm;Ie为供选择管径集合。
2.3 模型求解
分支定界法是解决这类非线性整数规划难题的有效手段,设优化问题为T,最优解为Topt,将不考虑整数条件的线性规划问题定为LTn。LTn与T问题的解的关系为:如LTn问题没有可行解,则T也没有可行解;如LTn问题有最优解,且符合整数条件,则LTn与T问题的最优解一致;如LTn问题有最优解,且不符合整数条件,则LTn问题的最优解为T问题最优解的下界,而T问题的任意可行解为一个上界。具体优化步骤如下:
<1> 设活点集合为{T},上界Tu=+∞,当前最优整数解为ϕ;
<2> 如活点集合=ϕ,则转到第<7>步,否则随机选择一个分支点,从分支点集合中去掉分支点n;
<3> 解n对应的松弛问题LTn,如问题无解,则转到第<2>步;
<4> 如点n对应的松弛问题LTn的最优解大于Topt,则点k被剪枝,转到第<2>步;
<5> 如点n对应的松弛问题LTn的最优解满足整数要求,则定义上界Tu=Tk,当前的最好解为Tk,否则转到第<2>步;
<6> 如点n对应的松弛问题LTn的最优解满足不整数要求,则生成点n的2 个后代点,令这2 个后代点为活点,加入活点集合,转到第<2>步;
<7> 如当前的最优整数解为ϕ,则原问题无解;否则,原问题的最优解为Topt,停止迭代,计算结束。
3 算例分析
3.1 基础数据
以某陆上20×104t/a 产油量的老油田为例,原有31 口油井、原有5 个阀组和25 口新增油井,老油田管网的坐标见图1。其中,阀组后面的括号内为其最大连头数量。
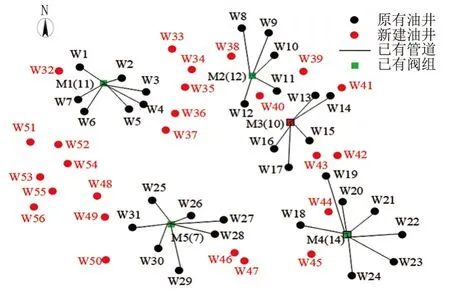
图1 老油田管网的坐标Fig.1 Coordinates of pipe network in old oilfield
3.2 优化结果
采用分支定界法对新增加密井和阀组进行布局优化,优化后的管网坐标见图2。靠近阀组M5 和M11 的新增油井都已就近接入对应阀组,剩余新建油井只能新增一座阀组,其坐标为(0.95,1.98),优化后新建管道的走向和长度见表1。管道长度合计15.43 km,考虑均采用D78 mm 的管径,管道单位长度的价格为117 元/m,单个阀组投资为425 万元,总投资为605.53 万元。

表1 整体优化后新建管道的走向和长度Tab.1 Direction and length of new pipeline after overall optimization
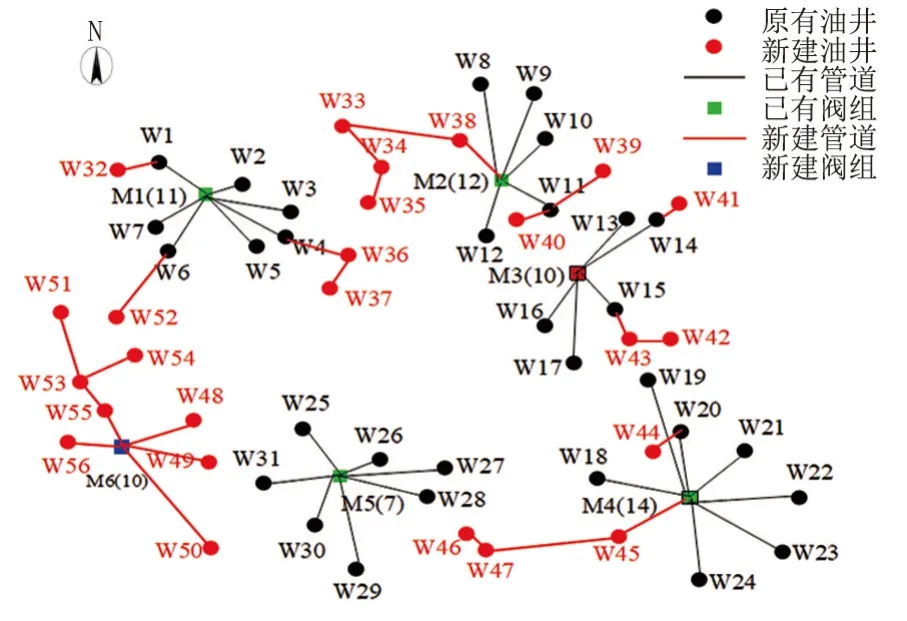
图2 优化后的管网坐标Fig.2 Pipe network coordinates after optimization
3.3 整体优化与分级优化对比
分支定界法为整体优化算法,此外传统分级优化也是常用的优化策略,即将每层的最优解拼凑而来[12-13],分级优化后的管网坐标和新建管道的走向和长度见图3 和表2。对于管网左侧的新增阀组位置有所变更,大部分新增油井通过放射状连接至新增阀组,枝状-放射状的管网结构较少;右侧的W41 井没有就近接入W14 井,W44 井没有就近接入W20 井,W42 井、W42 井的接入阀组也进行了重新调整,这是由于分级优化是按照先后顺序求解井组划分、站点位置和管网之间的结构关系等子问题,得到的问题不是全局最优解。管道长度合计16.54 km,考虑均采用D78 mm 的管径,管道单位长度的价格为117 元/m,单个阀组投资为500 万元(整体优化中M6 阀组的实际连头数量为8,分级优化中的实际连头数量为9,建站的时候要考虑2 个连头的富余量,故分级优化的阀组投资更大),总投资为693.52 万元。与整体优化结果相比,分级优化后的管道长度增加了7.19%,总投资增加了14.53%;按照每千米压降0.5 MPa 核算,整体优化后的管网在运行中可减少0.56 MPa 的压降,预计减少50 kWh/h,年节约电费22 万元。

表2 分级优化后新建管道的走向和长度Tab.2 Direction and length of new pipeline after classification optimization
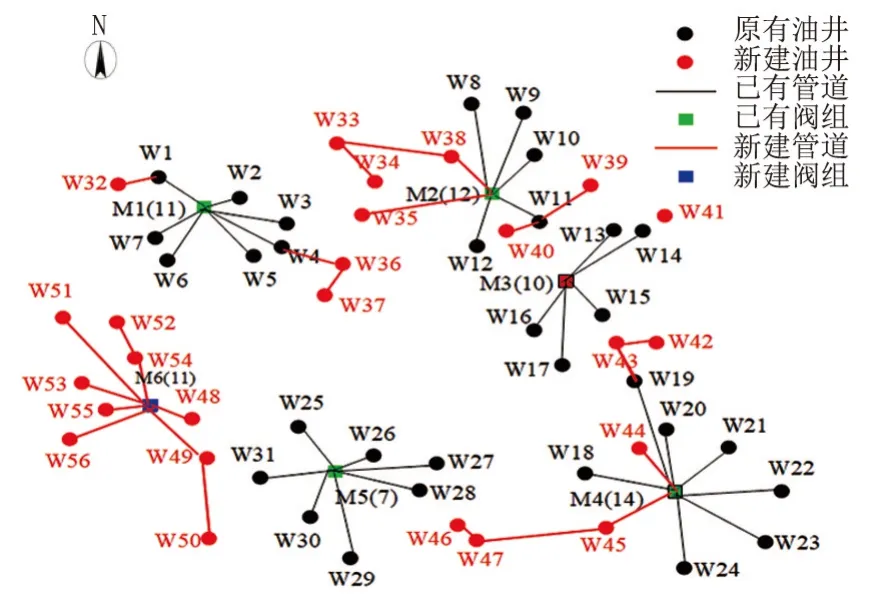
图3 分级优化后的管网坐标Fig.3 Pipe network coordinates after classification optimization
4 结论
1)以投资费用最少作为目标函数,在压力约束、管径集合约束、连头数量约束和隶属关系约束的前提下,通过分支定界法对新建油井和阀组的最优路径进行求解,实现了已有老油田集输管网的拓扑优化。
2)与整体优化结果相比,分级优化后的管道长度和总投资有所增加;整体优化后的管网在运行中可节约水力消耗,节能效果显著。
3)地形起伏及障碍物限制在实际管网布局中客观存在的,且算法的空间复杂性会随拓扑数量呈指数增长,今后应重点对三维地形下的集输管网实现高效布局优化。

