三维非刚体图像的特征挖掘定位算法
潘 燕
(福建农业职业技术学院 信息工程学院,福建 福州 350007)
目前,在机器视觉技术的支持下,从图像内挖掘特征实现目标定位的算法被应用于交通违章识别、海上目标定位、导航等领域[1-2]。但在日新月异的计算机技术和机器视觉环境下,图像特征挖掘定位算法已逐渐难以满足用户需求。
针对上述问题,相关学者研究了图像特征定位算法,如王保茎等[3]提出了图像特征关联定位算法,利用距离算法计算图像特征的欧式距离,并采用活动轮廓套索融合模型实现图像内目标的定位。方徐达等[4]提出了三维激光定位算法,通过提取目标图像的三维点云特征,使用特征匹配方法实现目标有效位置定位。上述方法均可实现图像内目标定位,但识别运动目标位置时的应用效果不佳。
三维非刚体图像是指当目标物体在受力或者运动情况下,其形状和大小不变,内部各点相对位置不变的物体图像。三维非刚体图像是定位目标位置的基础,为提升图像目标定位算法的应用效果,本文以三维非刚体图像为对象,设计了一种特征挖掘定位算法。在重建三维非刚体目标结构的基础上挖掘直线特征,并利用图像消影点方法处理图像内目标的视觉里程数据,从而推算出图像内的目标特征位置。
1 理论运用与特征挖掘定位设计
1.1 三维非刚体目标结构重建
通过摄像机采集目标非刚体图像,采用加速度平滑约束的非刚体三维结构重建方法得到运动目标图像的三维轨迹结构信息。
由于运动时非刚体目标具有复杂多变的特征[5],根据目标形状重建其三维图像时需估计其运动图像每一帧内的新形状基,并重新定义不同运动的形状基[6]。根据非刚体图像在不同时间帧中的信息变化情况,将图像信息转变为非刚体特征点,从而得到非刚体图像的三维轨迹结构信息。
令t为获得三维非刚体图像序列特征点的间隔时间,按照物理运动规律,则三维非刚体图像中第i帧中特征目标的平均速度为
式中:ΔJ为原始非刚体结构矩阵;Ji1、Ji分别为三维非刚体图像第1 帧、第i帧的非刚体结构矩阵。
依据式(1)得到目标运动平均速度,计算当前三维非刚体图像内目标轨迹系数如下:
式中:vi1为图像i第一帧内目标运动平均速度。
三维非刚体图像目标在一定时间段内的位移差和时间的比值可用于描述目标运动的平均速度,但在一段时间内,其目标的平均速度与加速度变化数值极小[7-8]。因此,需对其进行累加操作,其目标函数如下:
式中:I为总帧数;Ji+1、Ji-1为与Ji相邻的非刚体结构矩阵。
在式(3)内引入目标的运动平滑约束,则
式中:W、Q分别为三维非刚体图像的二维观测矩阵和摄像机旋转矩阵;λ1为平衡参数,其数值大于等于0。
令V∈A3I×3I为三维非刚体图像平滑矩阵,其中的A3I×3I为三维非刚体图像序列矩阵,则三维非刚体图像平滑矩阵如下:
式中:i、j均为三维非刚体图像帧序列。
将式(5)代入式(4),则有
通过式(6)可知,该三维非刚体平均速度累加目标函数为二次函数[9],且其存在全局最优解析解。在求解其全局最优解析解时,首先计算三维非刚体目标三维轨迹结构矩阵的梯度为
式中:S为轨迹结构矩阵;∂为偏导数;f(·)为自变量函数。
令式(7)结果为0,得到三维非刚体平均速度累加目标函数全局最优解析解如下:
其中,QT+λ1VTV矩阵的广义逆矩阵用QT+λ1VTV来表示。当QT+λ1VTV具备可逆性时,再次将式(5)代入式(4),重新计算;当QT+λ1VTV不具备可逆性时,式(8)所得结果为全局最佳解析解。
1.2 基于直线段检测的直线特征挖掘
以三维非刚体图像三维轨迹结构信息的梯度为基础,采用直线段检测算法[10]挖掘该三维轨迹结构信息内的直线特征,得到存在断裂的直线段,应对该直线段进行连接处理。令AB、CD为断裂的两条线段,η为线段AB与AD之间的夹角,β为DA和DC之间的夹角。当η与β符合以下条件时,则认为AB与CD为共线,则
式中:θ1、θ2均为线段的角度阈值;L为线段长度阈值。
当线段AB与CD满足式(9)时,则线段AB与CD为同一条直线。经过上述步骤,挖掘到三维非刚体图像三维轨迹结构信息内的所有直线特征。
1.3 基于图像消影点的视觉定位方法
将三维非刚体图像的三维轨迹结构信息内的直线特征作为输入,采用图像消影点方法获得三维非刚体图像内的目标方位元素。
令O1、O2分别为三维非刚体图像的相机标定矩阵、欧式坐标系旋转矩阵,则消影点位置矩阵如下:
式中:fx、fy均为焦距;u、v为三维非刚体图像内直线特征的消影点主点坐标;ζ、φ分别为目标位置朝向角和俯仰角。
由式(10)计算得到三维非刚体图像内直线特征的某个消影点数值,过程如下:
由于三维非刚体图像内直线特征消影点的坐标为齐次坐标[11-12]。因此,cosφcosζ数值为1。随机在非刚性目标中设置一点,将该点分别置于相邻的两幅图像内,分别由x、x′表示,按照单应性计算x与x′之间的关系如下:
式中:Z、t′分别为三维非刚体图像的移动距离与时间。
依据x与x′之间的关系,计算三维非刚体图像内目标的垂直视场如下:
式中:H为三维非刚体图像高度。
对式(13)进行转换,则有
计算相机光轴和物体光轴的角度如下:
式中:θ为相机光轴和物体光轴之间的角度。
将式(14)代入式(15)中,则有
依据平面几何理论,计算三维非刚体图像内目标的Y方向坐标为
式中:h为三维非刚体图像内目标高度数值。
依据上述公式结果,计算三维非刚体图像目标与摄像机之间的距离为
式(17)、(18)即为三维非刚体图像内目标的视觉里程,依据该视觉里程数据[13-15],推算t′时刻三维非刚体图像中待定位目标的位置如下:
式中:lt′为视觉里程位移数值;cosζt′为视觉陀螺仪估计朝向。
2 实验与结果分析
将交通管控路段内移动车辆的三维非刚体图像作为实验对象,采集其不同时段的移动车辆图像共4000张,采用三维非刚体图像的特征挖掘定位算法(以下简称“算法”)定位三维非刚体图像内目标位置,验证算法的实际应用效果。
2.1 三维非刚体目标结构重建测试
以某张移动车辆图像为实验对象,采用本文算法重建其三维非刚体目标结构,结果如图1所示。

图1 移动车辆三维非刚体结构重建测试结果
由图1可知,车辆三维非刚体结构与其原始图像内车辆形状完全吻合,且车头、车灯以及轮毂等细节也完全相同,说明本文算法能够有效重建移动车辆的三维非刚体结构,且重建后的移动车辆三维非刚体结构精度较高。
2.2 直线特征挖掘测试
挖掘三维非刚体结构内的直线特征是实现目标定位的基础,以一组车辆三维非刚体轨迹结构矩阵内的数据点集作为实验对象,挖掘该数据点集内的直线特征,结果如图2所示。
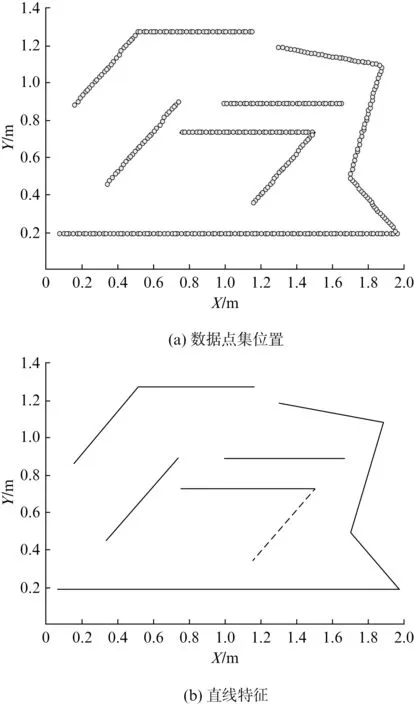
图2 直线特征挖掘结果
由图2可知,三维非刚体轨迹结构矩阵内的数据点集呈规则性直线型分布,而采用本文算法提取的该数据点集直线特征与原本的数据点集分布位置完全相同。图2(b)中存在虚线表示部分被遮挡的直线特征。这一结果说明算法提取三维非刚体轨迹结构矩阵内数据点集的直线能力较强,也从侧面说明算法对三维非刚体图像内目标定位能力较好。
以一张较为模糊的移动车辆图像中的某条轮廓线为实验对象,采用本文算法挖掘该直线特征,结果如图3所示。

图3 模糊三维非刚体图像直线特征挖掘结果
图3中,在初始图像内,三维非刚体轮廓线存在明显马赛克情况,其直线特征不够明显。采用本文算法提取该三维非刚体轮廓线后,其整体轮廓与初始图像内轮廓线路一致,并呈现的直线线条清晰。该结果说明算法在提取三维非刚体图像内轮廓直线特征时,受三维非刚体图像模糊程度影响较小,提取直线特征的能力优秀。
2.3 三维非刚体图像目标定位测试
以10组三维非刚体图像为实验对象,采用本文算法定位该10组三维非刚体图像内的目标位置,结果如表1所示。

表1 三维非刚体图像目标定位测试结果
由表1可知,采用本文算法定位的6、10号三维非刚体图像内目标与目标的实际位置完全相同,在定位剩余三维非刚体图像内目标时,X或Y方向均存在一定偏差。其中,X方向上的最大偏差数值为0.5m,Y方向上的最大偏差数值为0.4m。在较大的运动目标场景内,该偏差数值微乎其微。综上所述,本文算法能有效定位三维非刚体图像内目标,且定位结果较为准确。
以三维非刚体图像内目标朝向角作为衡量指标,测试不同时间时其朝向角变化情况,结果如图4所示。
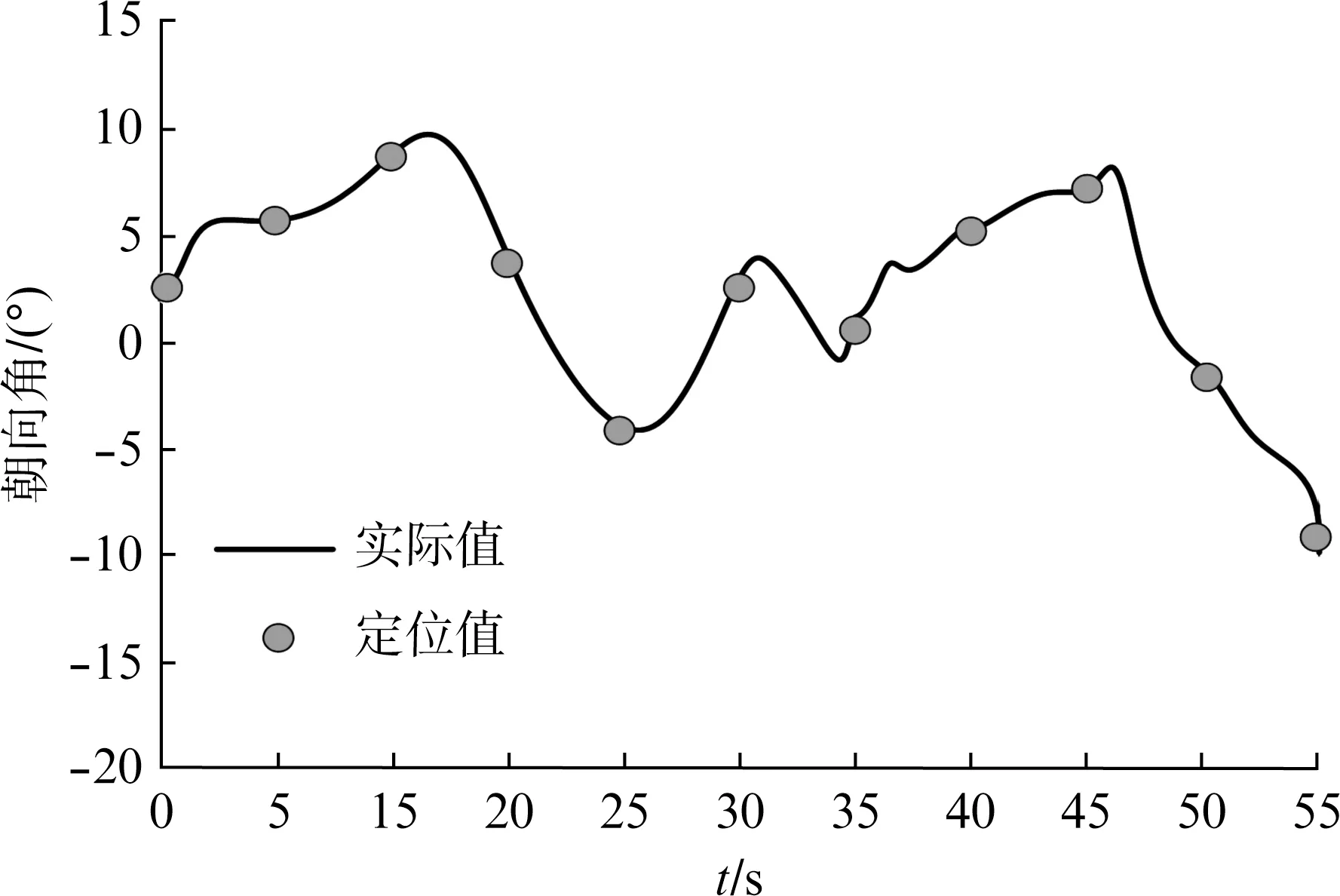
图4 三维非刚体图像内目标朝向角定位结果
由图4可知,目标的朝向角曲线随着时间的增加呈现波动趋势,而本文算法对目标朝向角的定位结果与其实际值曲线重合,说明本文算法定位三维非刚体图像内目标朝向角性能较强。
当三维非刚体图像内存在多个目标时,对获取目标定位存在一定影响。测试在三维非刚体图像内存在不同数量目标时,本文算法对目标定位的误差如图5所示。
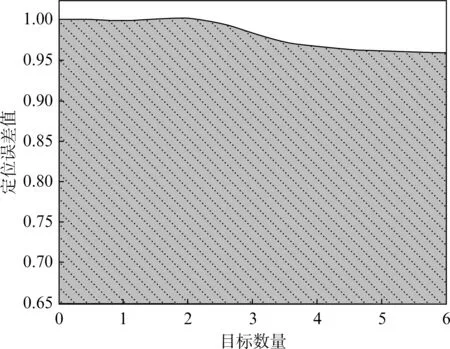
图5 目标定位误差
由图5可知,在目标数量少于2个时,算法定位三维非刚体图像目标精度均为1.0,随着三维非刚体图像内目标增加,算法对目标的定位误差呈现小幅度下降趋势。当图像内目标为6个时,算法定位目标误差依然高于0.95,说明本文算法定位三维非刚体图像目标受图像内目标数量的影响极小。
3 结论
按照重建三维非刚体目标结构、挖掘直线特征、视觉定位方法的思路,针对三维非刚体图像的特征挖掘定位算法展开研究,并在实际环境中对算法进行了多角度验证。根据实验结果可知:该算法构建的车辆三维非刚体结构与车辆自身结构吻合程度极高,具备较好的三维非刚体结构重建能力;挖掘三维非刚体轨迹矩阵结构内数据点集直线能力较强,并可有效定位三维非刚体图像内目标位置。在接下来的研究中,将考虑从提高挖掘定位时效性的角度,对该算法展开进一步优化。

