基于改进FCM 聚类分析方法的电力负荷特性研究
李富强,朱晨烜,骆利勤
(上海电机学院 电气学院,上海 201306)
随着人工智能领域的技术进步,一系列智能算法如专家系统、支持向量机和神经网络等已被广泛应用于电力负荷行业。但是,对于高维数据集,传统的智能算法计算过程过于复杂和耗时,不能保证对形状多样性的数据集的计算准确性[1]。近几年,聚类分析方法已广泛应用于电力负荷预测领域,根据电力负荷的特性,许多更精确的聚类分析方法被提出[2-3],这在学术界产生了影响。
在一些研究中,如文献[4]提出了结合K-均值(K-means)和反向传播神经网络的聚类分析方法,降低了负荷预测的误差。文献[5]提出了一种可能性C-均值(Possibilistic C-Means,PCM)算法,但PCM 聚类分析方法的聚类结果同样容易受到初始聚类质心选取的影响,导致聚类一致性问题。为弥补PCM 聚类分析方法的缺陷,文献[6-7]将PCM与模糊C-均值(Fuzzy-C Means,FCM)相结合,提出了一种可能性模糊C-均值算法。文献[8]提出了密度峰值聚类算法,能将任意形状的类簇进行聚类且具有很强的鲁棒性。文献[9]提出了一种在语义分割基础上,结合K-means和随机森林的聚类分析算法,提高了模型的准确性。文献[10]提出了改进K-means聚类分析方法,该方法减小了迭代次数,提高了聚类效率。文献[11]设计了一种基于最近邻与局部密度的自适应K-means聚类分析方法,通过结合近邻矩阵和局部密度以获取初始聚类质心,提高了传统K-means算法聚类效果。文献[12]基于中心指标和密度提出了Canopy二进制K-means聚类分析方法,使得聚类结果更精确,同时算法运行速度更稳定。文献[13]为解决传统模糊均值聚类算法中初始聚类中心选取不准确的问题,引入双尺度度量以提高聚类效果。
综上所述,上述算法仍有一些缺陷和局限性。例如,随机选择初始聚类质心可能会导致聚类结果陷入局部最优解,从而降低了聚类的准确性。因此,本文引入皮尔逊相关系数对欧氏距离进行改进,以获取初始聚类质心,然后使用FCM 聚类分析方法对聚类质心进行迭代更新,以获得更高精度的聚类质心。实验结果表明,改进的模糊聚类分析算法比传统的聚类分析算法更稳定、准确,可以有效地应用于负荷调度计划的制定,具有实际应用价值。
1 原始负荷数据预处理及特征指标权重赋值
1.1 畸变负荷曲线的剔除
畸变负荷曲线是指偏离聚类质心曲线的样本曲线。它们的存在可能会导致特征指标权重计算出现误差,并且还会影响聚类结果的准确性。而拉依达准则[14]在测量次数足够大时有很好的准确性,故本文采用该准则识别畸变数据。假设1组检测数据值含有随机误差,先计算出A′的列平均值和剩余误差Ejs,然后计算标准差θ。当|Ejs|>3θ,则此被认定为畸变数据应剔除。剔除畸变数据之后得到矩阵记为B。列平均值、剩余误差及标准差的具体表达式如下:
式中:m为样本数。
1.2 负荷数据归一化及特征指标提取
归一化的目的是将不同量纲的数据转换为统一的标准,以更好地进行比较、分析。均值方差归一化的公式为
式中:x为原数据集;μ为样本均值;s为样本的标准差。
通过减去均值对数据进行中心化处理,即改变平均值使得数据的平均值为零。这一操作不会改变数据分布中各个点之间的距离。标准差可被视为每个点距离平均值的平均距离,因此将数据除以标准差可以将数据中每个特征的距离量纲统一为标准差的倒数,从而保持数据点之间的距离不变。最终,数据被转换为具有零均值和单位方差的正态分布。将经过归一化之后得到的数据集记为矩阵C。
每小时采集一次原始数据,导致数据量大且维度高。直接使用所有数据聚类时间成本高,为了提高效率和降低维度,采用特征提取,提取关键指标如日负荷率、峰期负载率等,并对其进行优化处理。这样可以精确描述负载曲线的特性,提高效率并保留重要特性。在此基础上再进行负荷曲线的聚类,将矩阵C通过特征指标提取过后的数据矩阵记为矩阵D。
2 改进的FCM 聚类分析方法
为了解决FCM 聚类分析方法中聚类质心容易被划分到样本点密集区域的问题,对FCM 聚类分析方法进行了优化。然而,对于具有时序性和规律性的电力负荷曲线,如果两条负荷曲线之间的相似度仅依赖于欧氏距离,则得到的聚类效果不能反映电力负荷曲线的时序性和规律性特征。本文针对电力负荷曲线的聚类,将皮尔逊相关系数与欧式距离相结合得到改进的FCM 聚类分析方法。具体如下:
(1) 改进的FCM 聚类分析方法的局部密度
其中,改进后的欧氏距离为
皮尔逊相关系数
式中:dij为样本向量Xi到样本向量Xj的欧式距离;Nk(Xi)为数据点Xi的K个最近临近点;xis、xjs为样本向量Xi、Xj的第s维元素;n为样本向量的维度;γ为迭代次数;β为模糊指数;uij为第j个样本向量属于第i类的隶属度。
改进的FCM 集成聚类分析方法流程如图1所示。
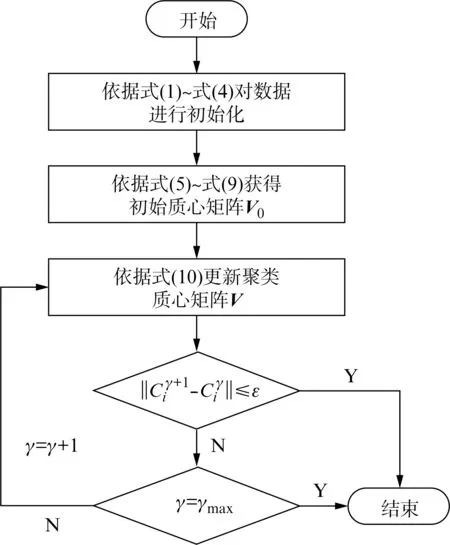
图1 改进FCM 聚类分析方法流程
3 经典聚类评价指数
本文以CH和XB聚类评价指数[15]目标函数为聚类评价指数。CH 聚类评价指数是根据计算类中样本向量到类质心向量的距离平方和来衡量类内相似度,其值越小代表相似性越高。通过计算CH 数据集样本质心向量与各类质心向量间的距离平方和来衡量类间差异度,其值越大差异性越大。因此,当目标函数JCH越大时,说明聚类精度越高。
XB聚类评价指数是根据各样本中向量与质心向量间的距离平方之和以及类质心向量距离平方来衡量的,向量与质心向量间的距离平方之和的值越小代表类内相似性越高;而质心向量距离平方的值越大代表类间差异性越大。因此,目标函数JXB越小,说明聚类精度越高。
4 实际电力负荷数据实验分析
为了验证本文算法的有效性和优越性,选取2022年某电网的实际负荷数据进行仿真。对负荷数据预处理,包括去除畸变负荷向量、降维处理、归一化处理、权重分配,然后提取最优的聚类曲线并分析聚类结果,最后比较算法。
4.1 负荷数据处理
4.1.1 负荷数据预处理结果分析 用于实例仿真的电力负荷数据一共包含全年的实测数据,每天每间隔一小时采集一次负荷值,共形成一个366×24的矩阵,构成366条电力负荷曲线,其原始电力负荷曲线如图2所示。
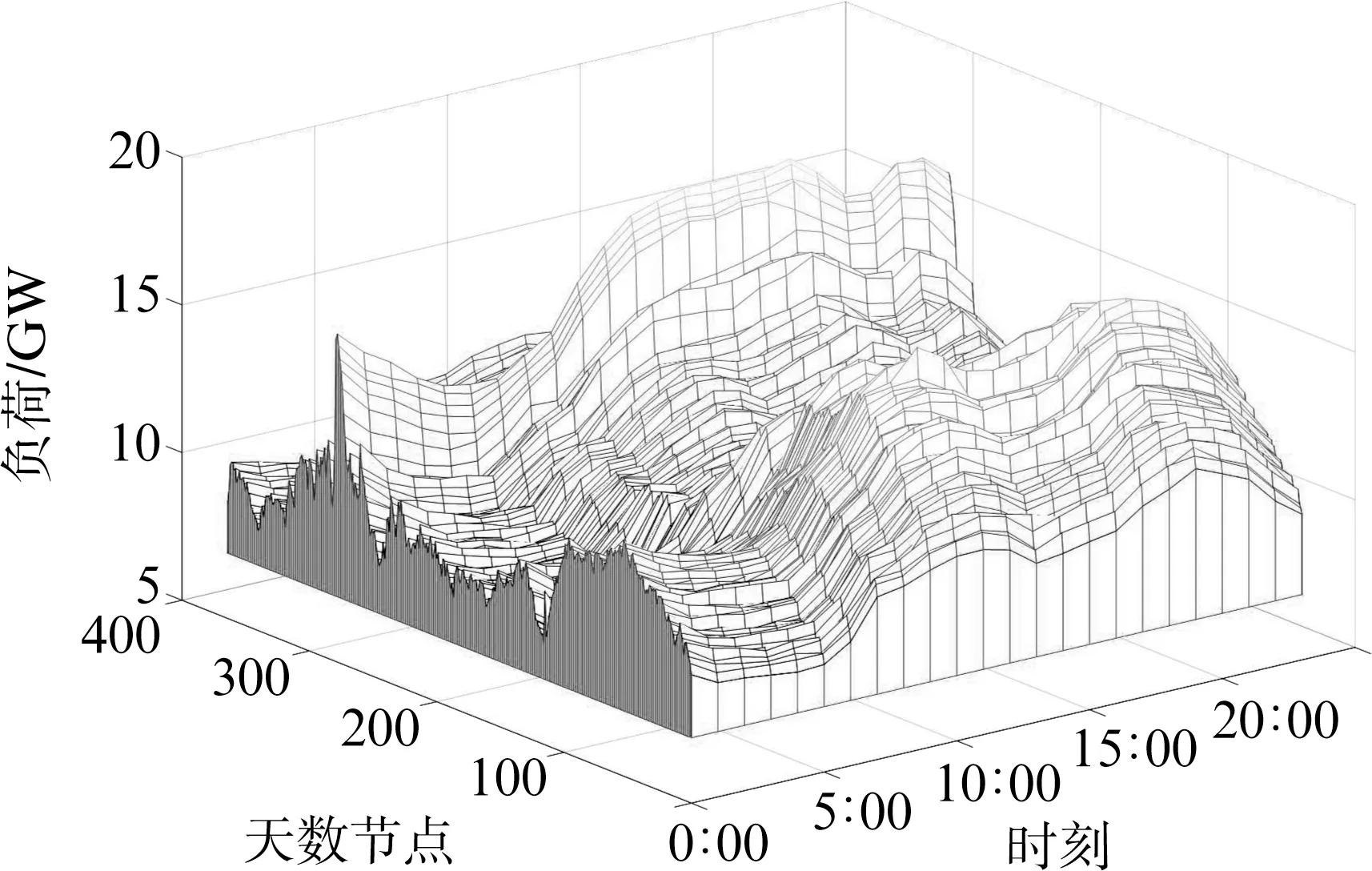
图2 原始电力负荷曲线
4.1.2 畸变负荷曲线的剔除 根据式(1)~式(3)将原始电力负荷数据集中的畸变负荷样本剔除,分析输出的畸变负荷样本向量,这些畸变负荷样本向量分别出现在2月1日到2月6日,该时间段正好是春节,6条负荷曲线相对于附近的负荷曲线,呈现出无规律性;4月3日至5日以及10月1日至7日分别是清明节和国庆节节假日,在此期间,大部分工厂、写字楼、学校的用电量明显下降;6月8日至6月10日温度骤升,后又恢复到8日前的温度,此期间,人们用空调比较频繁,电量明显上升。将剔除19个畸变负荷样本之后的矩阵记为B,剩下的负荷样本形成的电力负荷曲线如图3所示。
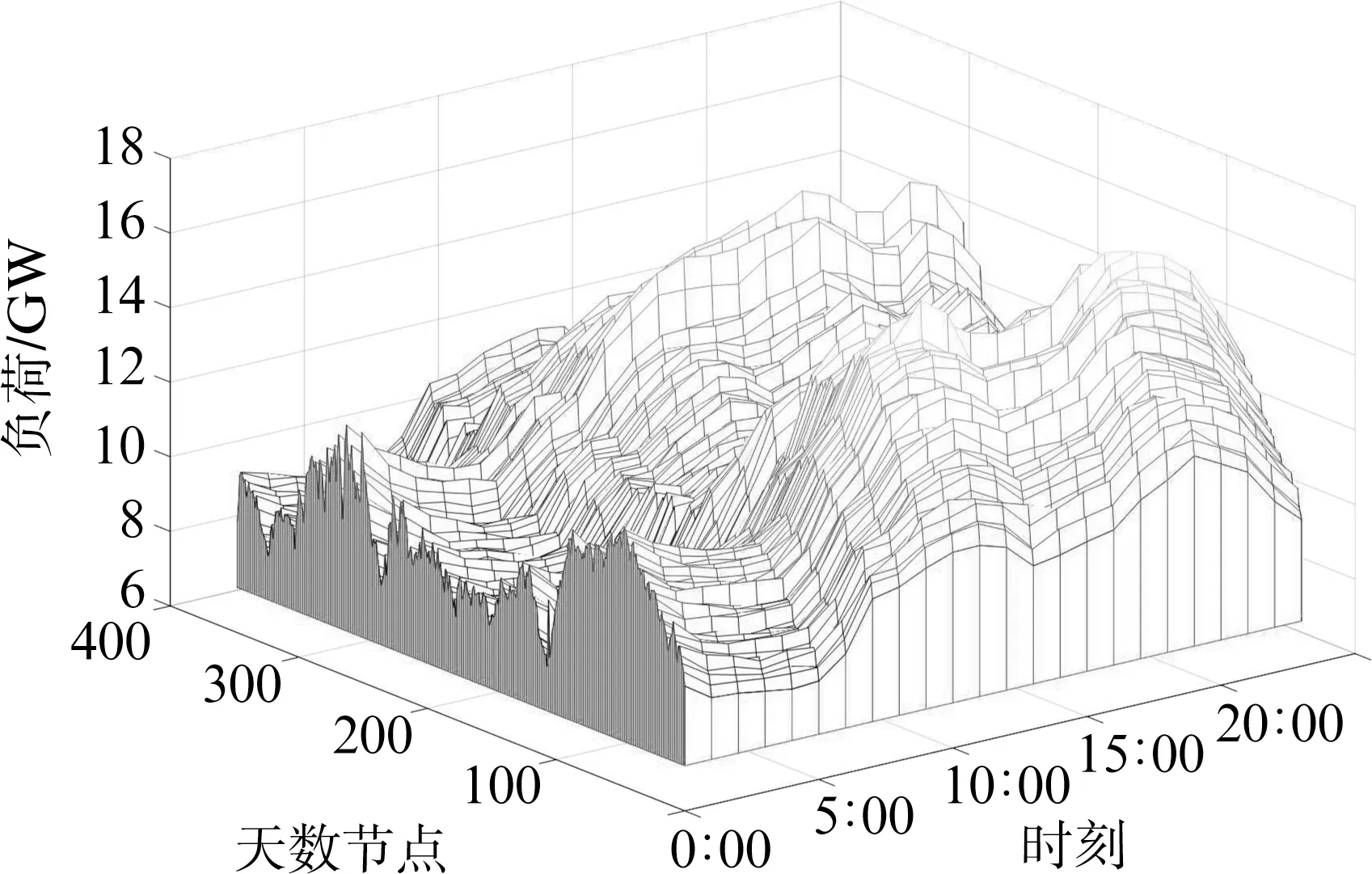
图3 剔除畸变负荷曲线后电力负荷曲线
对比图2、图3可知,图2中无规律和杂乱的负荷曲线已被剔除,剩下的负荷曲线都呈现出很强的规律性和时序性特点。剔除畸变负荷曲线后得到矩阵B,根据式(4)对矩阵进行归一化处理,所得矩阵记为矩阵C。从归一化后的矩阵C中提取特征指标进行降维处理,得到347×7的矩阵,记为矩阵D。
4.2 改进FCM 聚类结果分析
改进FCM 聚类分析方法是先通过改进聚类分析方法获取初始聚类质心,避免在FCM 聚类分析方法中由于随机选择初始聚类质心而引起聚类结果陷入局部最优解的问题。
导入预处理之后的矩阵D,在改进FCM 聚类分析方法中输入参数近邻数k=5;模糊指数β=2,ε=0.00001,最大迭代次数γmax=200,其聚类结果如图4所示。
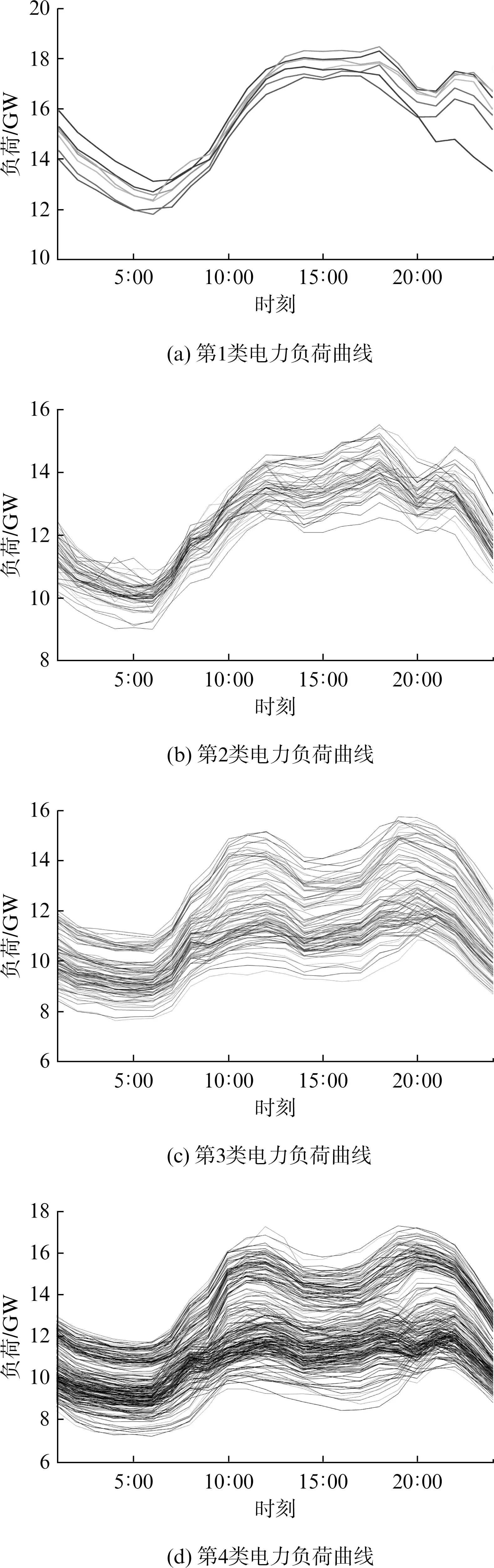
图4 改进FCM 的聚类结果
由图4可知,不同季节和场景下的负荷曲线呈现出不同的特点。在国庆节假日期间,第1类负荷曲线在11∶00~18∶00期间出现高峰,而在19∶00~24∶00之间,负荷变化相对平稳,这是由于服务业用电量急剧增加所致。第2类负荷曲线出现在冬季,两个峰值时段主要在人们用餐时间段,相对于其他负荷曲线,此类曲线在19∶00左右的负荷处于全天最高峰,因为此时段是人们集中洗漱的时间,对热水的需求量特别大。第3类负荷曲线出现在夏季,尽管受制冷设备影响,但是由于生活用热水需求量较少,热水器能够利用太阳能,因此负荷较低。此类负荷曲线没有特别明显的峰期时段,主要由于风扇、空调等制冷设备的不间断运行所致。第4类负荷曲线更能反映人们的日常生活规律,分别在11∶00和19∶00左右出现两个主要峰值,此时间段为用餐时段,人们日常家用负荷较大;此外,20∶00~22∶00为夜生活用电时间,负荷相对较高,很明显此类负荷曲线变化规律受温度的影响较小,更贴近于人们的日常生活规律。
4.3 聚类结果比较
聚类效果的评估主要取决于能否合理分配所有负荷曲线,而负荷曲线的合理分配主要考虑同类负荷曲线的相似性和不同类负荷曲线之间的差异。CH 聚类评价指数和XB聚类评价指数都是基于这两个方面进行考虑。表1给出了不同聚类分析方法下CH 聚类评价指数和XB聚类评价指数的比较结果,表2给出了不同聚类分析方法在聚类过程中的迭代次数和程序运行时间。
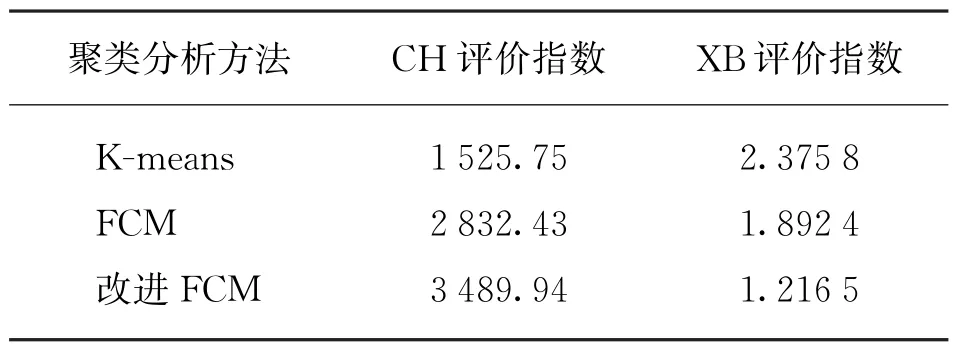
表1 不同算法下的聚类效果比较

表2 不同聚类分析方法的迭代次数和运行时间比较
由表1、表2可知,单一聚类分析方法所得到的CH 聚类评价指数明显低于改进的FCM 聚类分析方法所得到的值,而得到的XB聚类评价指数则相对较高。这表明,单一聚类分析方法得到的聚类效果相对较差,而改进的FCM 聚类分析方法则获得了更好的聚类效果。因此,利用改进的划分聚类分析方法来获得精确的初始质心,能够显著提高聚类的准确性。在迭代次数以及运行时间方面,改进的FCM 聚类分析方法明显优于K-means和传统FCM 聚类分析方法,表明利用改进的FCM 来获取精准的初始聚类质心能够提高聚类精度,并且能提升工作效率。
5 结论
本文提出的改进FCM 聚类分析方法,在传统FCM 聚类分析方法的基础上,将皮尔逊相关系数与欧式距离相结合得到改进后的欧氏距离表达式并进行聚类分析;对原始负荷数据进行预处理,包括剔除畸变负荷曲线、对剔除畸变负荷曲线后的负荷数据进行归一化处理,并从归一化后的数据中提取特征指标进行降维,提高了聚类分析的效率且保留了负荷重要特性。通过将本文方法与K-means、传统FCM 聚类分析方法做仿真对比,验证了改进FCM 聚类分析方法对电力负荷曲线聚类分析的有效性和优越性。本文方法在实例中获得了预期的聚类结果,但是对于日趋复杂多变的负荷数据,仍然有一些地方需要优化和改进,如对于不同来源的实际电力负荷数据,可对特征指标进行优化,加入一些必要的影响负荷变化的因素,例如温度和天气等。

