电动客车驱动系统机电耦合有限元建模及其响应

罗晶豪　蓝永庭　李俊明

摘 要：电动客车在服役过程中，受到电磁因素与机械因素的共同作用易出现驱动系统不寻常的扭转共振，容易导致齿轮等零部件失效。为探明原因从而解决这一问题，本文尝试从一种新的角度出发，综合考虑电池供电电路、电机电磁力及变速器等整个传动系统中轴的扭转弹性变形之间的机电耦合作用。运用麦克斯韦-拉格朗日方程与有限单元法，分别建立电池-电机子系统动态模型与机械传动系统动态模型，并在此基础上建立电动客车驱动系统的电磁非线性动态方程，再运用Newmark法对整体模型进行数值求解，给出了系统中几个关键节点的时域响应和频域响应。分析结果表明：在电机与变速器连接处的扭振现象较为严重，由于电流输入的不稳定性使得速度与加速度出现异常波动，系统出现频率为22、51、142 Hz的主共振、超谐波共振和亚谐波共振现象。本文可为进一步分析电动客车电传动系统的振动机理提供一种新的理论模型，为解决电动客车驱动系统零件失效的问题提供助力。

关键词：电动客车；非线性模型；驱动系统；机电耦合；扭振

中图分类号：TH113.1 DOI：10.16375/j.cnki.cn45-1395/t.2023.04.001

0 引言

汽车是当今社会重要的交通工具，国家十分重视汽车行业的发展，新能源汽车尤其是电动汽车更是当前发展的重点。在目前的新能源汽车行业领域，还存在一些技术障碍，主要表现为驱动电机技术与动力电池技术。电动汽车驱动系统的NVH（噪声、振动与声振粗糙度）问题会降低电机及其他零部件的使用寿命，并且影响车内人员的状态[1]，从而导致安全问题。而动力电池的不稳定放电会使得驱动系统的振动更为复杂，所以对电动汽车驱動系统的振动机理研究十分必要[2]。

电动汽车驱动系统的振动问题按照频率范围来分大致有3种：第1种是低频振动，频率范围大概在0～10 Hz，如突加/突减油门引起的车辆整体颤动；第2种是中频振动，频率范围大概在10～100 Hz，如变速器、行星齿轮等部分的振动；第3种是高频振动，频率范围大概在100～2 000 Hz，如机电磁耦合振动。当前对电动汽车电传动系统扭转振动问题的研究对象大多为家用汽车，并且对于机电耦合因素的影响多集中于对电机参数的控制与外部干扰因素上[3]。张元元等[4-5]建立了永磁同步电机的矢量控制模型，分析了引入谐波转矩的各电机参数对动力传动系统扭转振动的影响。闫军等[6]应用机电动力学综合考虑了系统的机械部分与电磁部分，建立了电力机车的机电动力学模型及相应的微分方程组，研究了机电耦合的相互作用规律。蔡敢为等[7]利用有限单元法建立了在高水头、大流量水流和强电磁场的共同作用下，考虑水轮发电机组的机电耦合关系和液、固耦合关系的非线性动态方程。李香芹等[8]考虑了传动系统中各齿轮的齿侧间隙，建立了一款二档变速器电动汽车从电机到车轮的传动系统整体非线性扭振模型，主要探究了齿侧间隙对传动系统扭振的影响。葛帅帅等[9]考虑永磁同步电机动态特性及齿轮传动系统非线性时变啮合特性，建立电动汽车电驱动系统机电耦合动力学模型，仿真分析在不同典型工况下的电动汽车电驱动系统齿轮系统扭转特性和电机定子电流的动态响应特性。Bai等[10]综合了电机的磁场因素与传动系统的时变刚度，建立机电耦合模型，研究了电机电压与传动系统负载瞬时变动下系统的振动。李韶华等[11]建立了电动汽车机-电-路耦合系统非线性动力学模型，分析了电磁激励、路面二次激励、车速和车辆非线性对车辆平顺性和道路友好性的影响。Qin等[12]考虑了空气阻力和路面不平度构成的外激励，建立了纵向-垂向耦合动力学模型，提出了电动汽车动态吸振结构，可减轻由道路激励和不平衡电磁力引起的振动负效应。以上文献对驱动系统扭振的影响因素都局限在电机与机械结构，均未考虑电源的不稳定因素对驱动系统振动的作用，该问题仍有许多原因不明，致使电动客车的运行安全隐患问题、NVH问题、续航问题依然存在。

本文将建立一种考虑电池放电特性因素[13]、联合电机与机械传动系统的电动客车驱动系统机电耦合扭转振动模型，用以进一步探究电动客车传动系统的振动机理，以期解决车辆运行时零件失效而导致的安全问题。同时，在此基础上还可以进一步探究在电磁激励与传动系统自身激励的共同联合作用下的振动机理，车辆微观振动行为与车载电池的电流、电压等不稳定因素的内在联系等，以期提高汽车的NVH性能及电池管理能力。另外在理论上，进一步完善与丰富车辆驱动系统的设计与控制理论，以及多场耦合非线性振动理论。

1 电池-电机子系统动态模型

首先，考虑电机中电场与磁场的干扰因素，将电机中产生的寄生电容、绕组电感等效分离成为电路中的独立部分，再将电机实体部分、电池等与之一起按照电动汽车实际的电路连接方式[14]组合形成电池-电机子系统动态模型，如图1所示。

1.1 电场能与磁场能

4 试验与算例结果

针对上述理论进行仿真计算，同时采用对应型号的电动客车（图8）进行实车台架检测实验，对比结果的准确性。在电动客车传动系统上的电机与变速器连接轴、变速器传动轴、车轮半轴上分别安装扭振传感器，如图9中编号1、2、3所示。控制电机转速为2 000 r/min左右并挂1档，测得其扭转振动情况如图10所示。

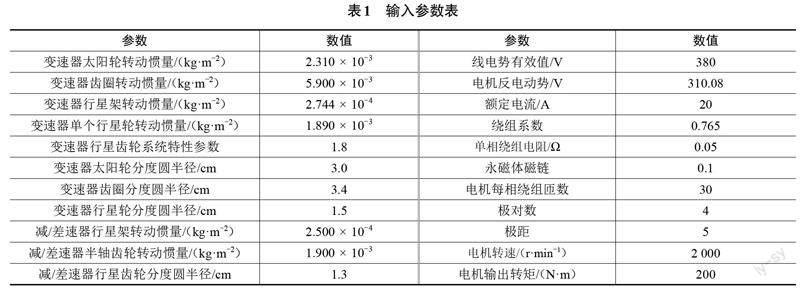
采用Matlab软件进行仿真计算，设置电机转速为2 000 r/min，并经过变速器1档传动。取在一般沥青上行驶的摩擦阻力、无风时的车辆迎风阻力，同时考虑车辆的加速阻力以及车载电池放电不稳定造成的电流异常波动，具体输入的参数如表1所示。计算得到1档传动时系统的前10阶系统固有频率，如表2所示。

4.1 时域分析

设置仿真时间为10 s，分500步进行，时间步长为0.02 s，得到系统节点4、14、22的角位移、角速度、角加速度的时域动态响应，如图11—图12所示。

从仿真角位移响应来看，各节点振动情况与实验数据基本吻合，说明仿真结果基本正确。

节点4和节点14的变形量明显大于节点22，两节点都处于变速器内部，与电机轴直接连接。说明此处除了电机传递的力矩外，还存在严重的电磁力作用，致使变形的波动变得复杂，幅值均在1.00×10-5 rad/s上下波动。节点4的幅值最大达到2.20×10-5 rad/s，节点14的幅值最大为1.70×10-5 rad/s。相对来说，节点22变形更加稳定且幅值较小，最大时达到4.70×10-6 rad/s。就总体变形趋势而言，各节点在一定变形的基础上呈现出扭转振动的特性。

受到电磁干扰与传动系统自身特性的共同作用，各节点角速度也呈现出一定的波动。由于电池电流经过逆变器后会转换成三相交流电流，所以随着电流的方向会发生磁场变化，对节点施加的力也会改变方向，使得角速度来回波动。且由于电池放电不稳定，致使角速度的波动幅值并不是恒定的，如图12中所示。受电磁干扰严重的节点4与节点14的角速度幅值绝对值最大时达到了2.98×10-6 rad/s，最小仅有0.80×10-6 rad/s。

角加速度从节点4到节点22逐渐减小，且从时间上看，角加速度变化周期逐步加长，反映出对节点作用的电磁力影响在逐渐减弱。

4.2 频域分析

电动客车运行时自身处于一个既有机电耦合作用又有路面激励的复杂环境中，系统可能发生主共振、次共振等多种共振现象。将以上时域结果转换成频域，如图13—图15所示。

图13（a）在频率22、51、142 Hz处出现明显峰值，说明节点4的振动主要由这些频率所贡献。对比系统的固有频率，22 Hz与[ω2]、51 Hz与[ω3]、142 Hz与[ω4]相接近，说明在节点4处主要发生了主共振，22 Hz与[ω3]/3相接近，说明此时节点4处同时伴有超谐波共振发生。图13（b）在22、142 Hz处出现明显峰值，同理，142 Hz与[ω4]相接近，说明节点14发生了主共振，22 Hz与[ω3]/3相接近，说明发生了超谐波共振。图13（c）在22、31、51、65 Hz处出现明显峰值，22 Hz与[ω2]、51 Hz与[ω3]、65 Hz与[ω3]相接近，说明在节点22处发生了主共振，31 Hz与3[ω2]/2相接近，说明节点22处发生亚谐波共振，22 Hz与[ω3]/3相接近，说明发生了超谐波共振。

图14与图15的频域峰值分布大致相同，只是幅值大小有差异。对应角位移的频域分布，两图中图（a）均在频率为22、51、142 Hz时出现明显峰值，两图（c）在31、65 Hz处亦有明显峰值，进一步说明了系统各节点存在共振现象。同时，从图中可以看出，节点4、14的速度与加速度幅值波动更加具有突变性，幅值总是在相近的频率处发生较大的变化，比如节点4处的速度最小值2.00×10-7与最大值8.87×10-6交替出現，加速度亦是如此。而节点22的速度与加速度的幅值变化相对平稳，各频率间呈现逐渐减弱的趋势。这是因为节点4与节点14处所受的电磁干扰更加严重，而由于受到电池放电（输出电流）的不稳定性影响，电磁力总是发生突变，致使两节点的速度与加速度表现出突变的特点。而节点22处电磁干扰较弱，所以幅值变化较为平稳。

5 结论

本文针对车载电池的不稳定放电特性与传动系统自身的振动特性，结合麦克斯韦-拉格朗日方程与有限单元法建立了包含电池-电机子系统动态模型和机械传动系统动态模型的电动客车驱动系统非线性动态模型。同时，考虑车辆运行时的环境阻力因素，采用Newmark法对模型进行了数值计算，获得了系统前10阶固有频率以及节点4、14、22的位移、速度、加速度的时域及频域动态响应情况。结果表明：

1）在电磁干扰的作用下系统存在着明显的扭振现象，且表现出复杂的非线性特征，同时有着主共振、超谐波共振、亚谐波共振等多种共振现象并存。

2）模型较好地体现出了电池放电特性对电动客车驱动系统的扭转振动的影响，表现出了一些以往的方程没能够反映的动态特性。

3）在以后的研究中，可进一步探究在车辆不同工作状态下，电池放电特性、路面激励的耦合作用对传动系统振动的影响，进一步充实和完善电动客车的设计制造理论，为车辆的安全运行和使用寿命做出贡献。

参考文献

[1] 吴文栋，马紫辉，刘志恩，等. 某SUV车内低频轰鸣声问题分析与优化[J].广西科技大学学报，2020，31（2）：86-92，125.

[2] 赵雨.关于新能源汽车发展存在的障碍及其解决措施研究[J].时代汽车，2021（17）：133-134.

[3] 严正峰，尹大乐，张农，等.汽车动力传动系统振动问题及解决方法综述[J].合肥工业大学学报（自然科学版），2021，44（3）：289-298，356.

[4] 张元元，于蓬，王健.电机参数对电动车传动系统扭转振动的影响分析[J].机电工程，2020，37（2）：144-149．

[5] 刘成强，徐海港，柴本本，等.纯电动汽车传动系统扭转振动特性分析[J].机械设计与制造，2018（12）：223-226.

[6] 闫军，姚代祯，周志霞.电力机车机电动力学模型的构建与分析[J].高技术通讯，2019，29（6）：602-606.

[7] 蔡敢为，蓝永庭，李兆军，等.混流式水轮发电机系统的动态模型及响应[J].吉林大学学报（工学版），2009，39（4）：976-981.

[8] 李香芹，曹青松，高小林.含齿侧间隙两挡变速器电动汽车传动系统扭振分析[J].噪声与振动控制，2021，41（4）：142-149.

[9] 葛帅帅，杨雨番，郭栋，等.电动汽车电驱动系统机电耦合动态特性研究[J].重庆理工大学学报（自然科学版），2021，35（5）：50-57.

[10] BAI W Y，QIN D T，WANG Y W，et al．Dynamic characteristics of motor-gear system under load saltations and voltage transients[J].Mechanical Systems and Signal Processing，2018，100：1-16.

[11] 李韶华，罗海涵，冯桂珍，等.电动汽车机-电-路耦合系统建模及动力学分析[J].机械工程学报，2021，57（12）：51-61.

[12] QIN Y C，HE C C，SHAO X X，et al. Vibration mitigation for in-wheel switched reluctance motor driven electric vehicle with dynamic vibration absorbing structures[J].Journal of Sound and Vibration，2018，419：249-267.

[13] 梁伦，杨年炯，吴秋满，等. FSEC方程式赛车电池充放电特性研究[J].广西科技大学学报，2019，30（2）：20-24.

[14] 黄彩娟.纯电动汽车电路图组成与识读方法——以德系车型大众ID4车型为例[J].专用汽车，2022（7）：76-78.

[15] 何逢春，贾晓宇，陈敏，等.电动汽车永磁同步电机分布参数提取研究[J].电源学报，2019，17（5）：177-185.

[16] 王秀和.永磁电机[M]. 2版.北京：中国电力出版社，2011.

[17] 于吉坤，李立毅，张江鹏，等.定子开槽永磁同步电机气隙比磁导解析计算[J].电工技术学报，2016，31（S1）：45-52.

[18] 丁鸿昌，刘鲁伟，吕楠，等.表贴式永磁同步电机气隙磁密的计算与分析[J].计算机仿真，2018，35（4）：179-183.

[19] 王勖成.有限单元法[M].北京：清华大学出版社，2003.

[20] 邱家俊.机电分析动力学[M].北京：科学出版社，1992.

[21] 韩星会，王兆俊，华林.非圆锥齿轮防滑差速器动力学模型的建立方法：201810433298.3[P].2020-09-01.

Finite element modeling of electromechanical coupling and response in electric bus drive system

LUO Jinghaoa， LAN Yongting*a， LI Junmingb

（a.School of Mechanical and Automotive Engineering; b.School of Electronic Engineering， Guangxi University of Science and Technology， Liuzhou 545616， China）

Abstract： In the service process of electric buses， the unusual torsional resonance of the drive system often occurs due to the joint action of electromagnetic and mechanical factors， which easily leads to the failure of gears and other parts. To solve this problem， this paper tries to consider the electromechanical coupling between the torsional elastic deformation of the shaft in the whole transmission system including the battery power supply circuit， the electromagnetic force of the motor and the transmission. Using Maxwell-Lagrange equation and finite element method， the dynamic model of battery-motor subsystem and the dynamic model of mechanical transmission system are established respectively. On this basis， the electromagnetic nonlinear dynamic equation of electric bus drive system is established. Then Newmark method is used to solve the whole model numerically， and the time domain response and frequency domain response of several key nodes in the system are given. The analysis results show that the torsional vibration at the connection between the motor and the transmission is the most serious， and the instability of the current input makes the speed and acceleration fluctuate abnormally， resulting in the main resonance， super harmonic resonance and sub harmonic resonance of the system with frequencies of 22， 51 and 142 Hz. This paper can provide a new theoretical model for the further analysis of the vibration mechanism of the electric transmission system of electric buses and help solve the parts failure of the drive system of electric buses.

Key words： electric bus; non-linear model; drive system; electromechanical coupling; torsional vibration

（責任编辑：黎 娅，于艳霞）

收稿日期：2023-02-12

基金项目：国家自然科学基金项目（12262003，11862002）；广西自然科学基金项目（2022GXNSFAA035537）；广西科技大学博士基金项目（校科博21Z13）资助

第一作者：罗晶豪，在读硕士研究生

*通信作者：蓝永庭，教授，硕士生导师，研究方向：机构动力学，E-mail：100000877@gxust.edu.cn