Links Fault Tolerance Analysis for Enhanced Hypercube Qn,3 Based on h-extra Edge-Connectivity∗
SUN Yali,ZHANG Mingzu
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)
Abstract: Design and maintenance of parallel processing systems depend greatly on reliability measures for parallel processing systems. The h-extra edge-connectivity provides a more accurate parameter for assessing the fault tolerance and reliability of interconnection networks of these systems under widespread defective links. The(n,3)-enhanced hypercube Qn,3 was proposed by Tzeng and Wei in 1991. We investigate the h-extra edge-connectivity of (n,3)-enhanced hypercube Qn,3, λh(Qn,3) behave a concentration phenomenon. And for an integer and n ≥9,the exact value of λh(Qn,3)concentrates on the 2n-1.
Key words: interconnection networks; reliability and links fault tolerance; concentration phenomenon, enhanced hypercubes;h-extra edge-connectivity
0 Introduction
Engineering designers are compelled to develop parallel processing systems with millions of processors due to the increasing demand for the processing and storing of enormous amounts of data. Certain processors and links will invariably experience some level of malfunction throughout the operation and maintenance of parallel processing systems for a variety of reasons. A connected graphG= (V,E) can be used to represent the interconnection networks in parallel processing systems, whereV(G) defines the set of processors andE(G) specifies the set of communication links between processors.The reliability and fault tolerance of interconnection networks are reflected by two key parameters: the connectivity κ(G)and edge-connectivity λ(G). The variety of connectivity characterizes the fault tolerance and reliability of interconnection networks. Generalized connectivity has received much attention from scholars[1–5]. In massive parallel computing networks,individual components may actually have varying levels of reliability. For example,processors next to one another or linksnear one processor cannot both be at risk of failure at the same time. As a result, Harary[6]proposed a number of novel variations on the edge-connectivity of graphs known as conditional edge-connectivity in 1983. And then theh-extra edgeconnectivity are proposed by F`abrega et al.[7]in 1996. The minimum cardinality of all theh-extra edge-cuts ofGis known as theh-extra edge-connectivity,represented as λh(G). For the vertex setX⊂V(G),let[X,]Gbe the edge-cut ofGcomposed of edges with one end inXand the other in. If there is no ambiguity,theGin[X,]Gcan be omitted. Let ξm(G)=min{|[X,]|:G[X]is connected}. It is said to be λh-optimal if λh(G)=ξh(G);otherwise,it is not λh-optimal. Many authors studied exact values of theh-extra edge-connectivity of some important classes of the interconnection networks,such as hypercubes[8],folded hypercubes[9–13],BC networks[14-15].
Based onn-dimensional hypercubeQn,Tzeng et al.[16]proposed the concept of enhanced hypercubeQn,kfor 1 ≤k≤n-1,by adding extra different types of complement edges. The enhanced hypercube differs from the hypercubeQnin that it has a smaller diameter,a better mean vertex distance. In particular,the(n,1)-enhanced hypercubesQn,1isn-dimensional folded hypercubesFQn.
Recently, the λh(Qn,k)and κg(Qn,k)are widely investigated. Sabir et al.[17]investigated λh(Qn,k)forh=1,2; Xu et al.[18]studied λh(Qn,k)in the intervalLi et al.[19]studied κg(Qn,k)forg=1,2,and 3; Sabir et al.[17]also determined κg(Qn,k)forg=1,2;Yin et al.[20]proved κg(Qn,k)for
In 2013,Li et al.[1]investigatedandn≥4.In 2014,Zhang et al.[15]studied λh(Bn)forandn≥4. In 2014,Yang et al.[21]investigated κg(Qn)for 0 ≤g≤n-4. In 2017,Zhou[22]studied κg(HLn)for 0 ≤g≤n-3 andn≥5. Sincehorgis very small,they usually satisfy the λh-optimality λh(G)=ξh(G)or κg-optimality
They also allow a linear number of malfunctions. For every integerh1≤h≤h2,λh(G)is equal to a constant, one then says that the λh(G) is concentrated for the intervalh1≤h≤h2, and represents a concentration phenomenon. If the boundsh1andh2are sharp,it means that this intervalh1≤h≤h2is maximal. In particular, forh1=h2, λh(G) = ξh(G) is λh-optimal. Fornis odd or even,dr= 4 anddr= 2 respectively, Zhang et al.[11]studied the values of λh(FQn)concentrate onFornis odd or even,dr=4 anddr=2 respectively, so Xu et al.[18]investigated the values of λh(Qn,k) focus onforAs far as we know, the study of the concentration phenomenon of λh(Qn,k) has just started. Inspired by above results, the most obvious concentration phenomenon of λh(Qn,3)in the subintervalis the primary emphasis of this paper. As|V(Qn,3)|is 2n,λh(Qn,3)is well-defined for 1 ≤h≤2n-1.
We have the main result about λh(Qn,3).
Theorem 1For two integersn≥9 and
The remainder of this essay is structured as follows. Section 1 introduces some related definitions and lemmas. Section 2 proves some important lemmas for the function ξm(Qn,3). Section 3 determines that the value of the λh(Qn,3)concentrates on a constant 2n-1. The last section concludes our results.
1 Preliminaries
For a positive integerh, the minimum cardinality of a set of edges whose deletion disconnectsGand each remaining component has at leasthvertices is called theh-extra edge-connectivity,represented by λh(G). LetF1be a minimumh-extra edge-cut of connected graphG. It is true thatG-F1has two components exactly. This paper requires thatG[X]andG[]are both connected,whereas the original definition of ξm(G)merely calls forG[X]to be connected.After changing this constraint,the function ξm(G)of(n,3)-enhanced hypercubesQn,3does produce the same outcome. Let
For at-regular graph,
whereexm(G)is twice the maximum number of edges among allmvertices induced subgraphs.
By the definition of the λh(G),ξm(G)offers the upper bound for the λh(G)for allSo,the functionλh(G)(by Zhang et al.[12]),
In this paper, the vertexx=xnxn-1···x1of the (n,3)-enhanced hypercubesQn,3can be conveniently denoted by the decimal integer
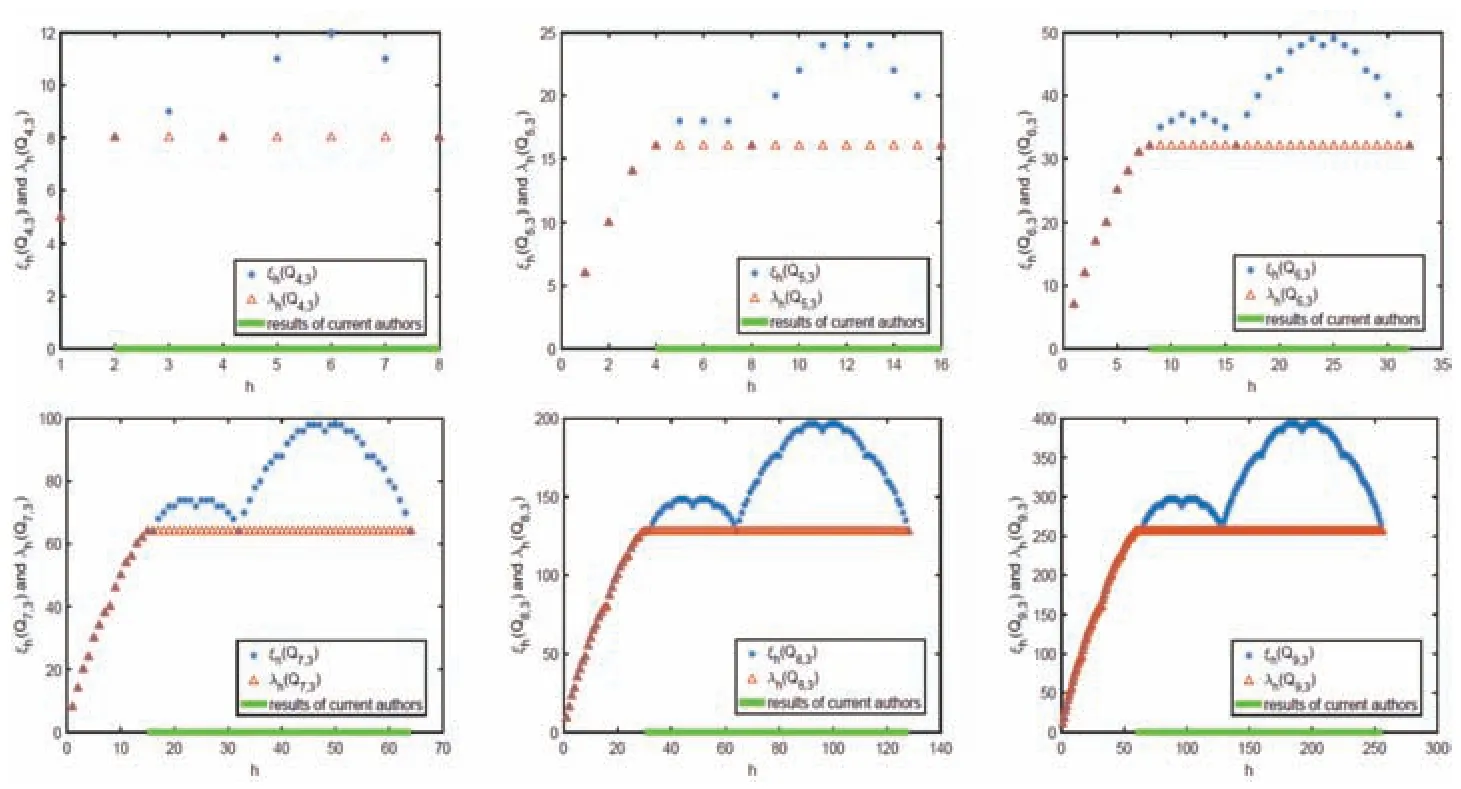
For any verticesx=xnxn-1···x2x1andy=ynyn-1···y2y1,the edgee=xyis calledk-complementary edges(1 ≤k≤n-1)if and only ifyi=xiforn-k+1 The definitions of then-dimensional hypercubesQnand(n,3)-enhanced hypercubesQn,3are stated as follow. Definition 1[23]The graph with 2nvertices known as then-dimensional hypercube has the symbolQn. The set of alln-bit binary strings is represented by the vertex setV(Qn)={xnxn-1···x2x1:xi∈{0,1},1 ≤i≤n}. Any pair of distinct vertices inQnare adjacent if and only if their labels differ in exactly one-bit position. Definition 2[16]The (n,3)-enhanced hypercube, denoted byQn,3(n≥4), is defined to be a graph with the vertex setV(Qn,3) = {xnxn-1···x2x1:xi∈{0,1},1 ≤i≤n}. If one of the following two criteria is met byy, then two verticesx=xnxn-1···x2x1andy=ynyn-1···y2y1are adjacent: The(n,k)-enhanced hypercubeQn,k(1 ≤k≤n-1)is obtained from the hypercubeQnby addingk-complementary edges between a pair of verticesx=xnxn-1···x2x1andin two (n-k)-dimensional sub-cubes. Note thatQn,1is the folded hypercubeFQn. In Fig 1, the enhanced hypercubesQ3,1andQ4,3are depicted. The scale ofQn,3expands exponentially as the integernincreases,and the topological structure ofQn,3becomes highly complex. Fig 1 Q3,1 and Q4,3 Letmbe a positive integer andbe the decomposition ofmsuch thatandt0>t1>···>ts.QnandQn,3have the same vertex set{0,1,···,2n-1}(under decimal representation). LetSm={0,1,···,m-1},andbe the corresponding set represented byn-binary strings. These conditions are used throughout the article when not causing ambiguity. Letbe the subgraph induced byinQn,3. Bothare connected. The subgraphs induced byinQn,3form≤8 are shown in Fig 2. Harper[24],Li et al.[1]independently obtained the exact expression of the functionexm(Qn). Lemma 1[1,24]for an integer Lemma 2[1]For Arockiaraj et al.[25]obtained the exact expression of the functionexm(Qn,k)in 2019,which was rewritten by Xu et al.[18]in 2021. Theorem 2[18,25]Ifthen Lemma 3[18]For positive integers 1 ≤m≤2tand 0 ≤t≤n,exm(Qn)≤tmandexm(Qn,k)≤(t+1)m. The monotonic interval and fractal nature of the function λh(Qn,3)have a significant impact on the precise value of the function ξm(Qn,3). The characteristics of function ξm(Qn,3)are described in the following. Fornis odd or even,f=1 andf=0,respectively. To deal with the interval(11×2n-1)/48≤m≤2n-1, by insertingn/2+1 numbers ofmn,rsatisfying and this interval will be divided inton/2numbers of integer subintervals. Forr= 1,2,···,n/2,mn,ris specified as the following expression: By calculation,it can be obtained that Lemma 4[18]For three integers Lemma 5For two integersn≥9 andr=1,2,···,n/2, ProofAccording to different expressions ofmn,r,there will be five cases in the proof. Case 1Forby Theorem 2,it can be obtained that Case 2Forby Theorem 2, Case 3Forr=n/2-2,mn,r=2n-3,by Theorem 2,it is not difficult to see that Case 4Forr=n/2-1,mn,r=2n-2,by Theorem 2, Case 5Forr=n/2,mn,r=2n-1,by Theorem 2, From the above five cases,it can conclude thatThe proof is completed. Lemma 6Given three integers ProofAccording to different expressions ofexm(Qn,3),there will be three cases in the proof. The value ofexp(Qn) forp< 22r-1-fis uniquely defined by the binary representation ofp. Therefore,exp(Qn) =exp(Q2r-f-1). By Theorem 2,is an edge cut ofQ2r-f-1. SinceQ2r-f-1is connected graph,and if one deletes the edge cuttwo induced subgraphs byandare connected, the edge cutofQ2r-f-1does exist. By Lemma 3,exp(Q2r-f-1) ≤(2r-1-f)p, and (ii)2n-3 Ifr=-2,thenmn,r=2n-3. Letm=2n-3+p1,where 0 ≤p1<2n-3. By Theorem 2 and Lemmas 1∼3,we can obtain The proof is the same as(i). It can be obtained that ξm(Qn,3)-ξ2n-3(Qn,3)=ξp1(Qn-3)≥0. (iii) 2n-2≤m≤2n-1. For an integerksatisfyingtk≥n-2 andtk+1≤n-3,m=t′×2n-2+xandt′= If 0 ≤x<2n-3,by Theorem 2 and Lemmas 1∼3, If 2n-3≤x<2n-2,thentk+1=n-3,x=By Theorem 2 and Lemmas 1∼3, Hence,the result holds. The proof of Theorem 1Given each integerh,forthere exists an integerr,satisfyingmn,r≤h≤mn,r+1. By Lemma 5 and Lemma 6, λh(Qn,3) = min{ξm(Qn,3) :mn,r≤h≤m Remark 1Forthe lower and upper bounds ofhare tight. (i)Ifnis even,ThenNote thatIfnis odd,ThenSimilarly it can see thatTherefore,the lower bound is sharp. (ii) As |V(Qn,3)| = 2n, by definition λh(Qn,3) that there are at least two components with at leasthvertices, the upper bound of the above interval is 2n-1. Thus,the upper bound is sharp. Remark 2For three integersthere existsrsatisfiesmn,r≤h≤mn,r+1.It is λh-optimal(λh(Qn,3)=ξh(Qn,3)=2n-1)if and only ifh=mn,rorh=mn,r+1. Ifh=mn,rorh=mn,r+1, by Theorem 2 and Lemma 5, λh(Qn,3) = ξh(Qn,3) = 2n-1. Ifmn,r To make our results in a more intuitive way, the scatter plots of ξh(Qn,3)and λh(Qn,3)are plotted in Fig 4. We plot the ξh(Qn,3)and λh(Qn,3)marked by the “∆” and “∗” scatters for 4 ≤n≤9,respectively. The result of this article is represented by the green lines in Fig 4. Fig 4 The scatter plots of λh(Qn,3)and ξh(Qn,3)for case 4 ≤n ≤9 Unexpectedly,we discover that the λh(Qn,3)exhibits a concentration phenomenon for integerLetg(n)=|{h: λh(Qn,3)=2n-1,h≤2n-1}|. Sois well-defined for any integer 1 ≤h≤2n-1. LetR(n) =g(n)/2n-1be the percentage of the number of integerhwith the corresponding λh(Qn,3)=ξh(Qn,3)=2n-1for 1 ≤h≤2n-1. Then Theh-extra edge-connectivity provides a more accurate assessment to assess the fault tolerance and reliability of these networks under large scale faulty links. This study demonstrates that the λh(Qn,3)exhibits a concentration phenomenon in the subintervalforn≥9. The ratio of the length of the λh(Qn,3)=2n-1subinterval to the 0 ≤h≤2n-1interval gets infinitely closer to 37/48 asngrows. Forn→∞, 77.083% values ofh≤2n-1, the λh(Qn,3) concentrate on a constant 2n-1.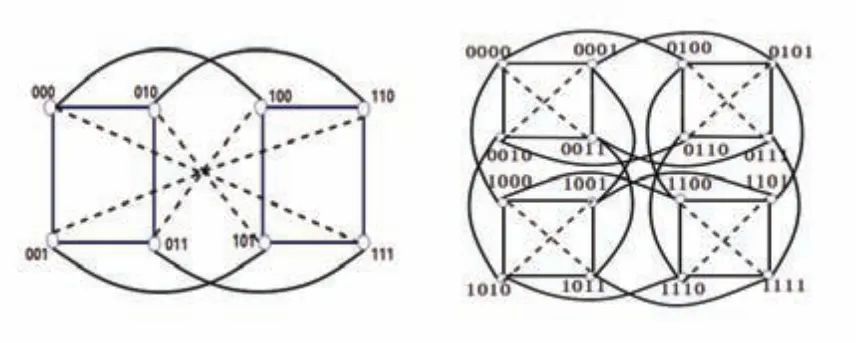
2 Some properties of the function ξm(Qn,3)
3 The value of λh(Qn,3)concentrates on 2n-1 for
4 Conclusions

