二维线性模组空间运动误差实时测量

娄志峰， 张汉平， 周竞杰， 张记云， 钱 钧， 范光照

（1. 大连理工大学 机械工程学院，辽宁 大连 116024；2. 大连理工高邮研究院有限公司，江苏 高邮 225600）

1 引 言

二维直线运动平台广泛应用于电子元件封装、3D 打印机和坐标测量等领域［1-3］。组成二维平台的单根导轨存在6 项几何误差：3 个位置误差（轴向定位误差、水平直线度误差和竖直直线度误差）和3 个姿态角误差（偏摆角误差、俯仰角误差和滚动角误差）［4］，几何误差是影响平台空间位置精度的重要因素［5］。对导轨的多自由度误差进行测量，并建立二维线性模组的空间误差模型对提升模组的应用范围尤为重要。

激光测量广泛应用于导轨运动误差测量领域。Huang 等［6］基于全反射原理、郭俊康等［7］运用光学与倾角传感器组合的方式分别设计了五自由度运动误差测量系统，美国 API 公司［8］基于单光束准直测量法研制了六自由度测量系统，Chang 等［9］基于多测头组合式激光光栅干涉提出了六自由度位姿测量方法。上述方法均可实现导轨多自由度运动误差的测量，缺点则是光路比较复杂、成本高［10］。

在导轨的6 项几何误差中，滚动角误差较难测量［11-12］。目前，水平仪是滚动角误差测量的主要设备，但水平仪无法测量竖直轴运动的滚动角误差［13-15］。Jin 等［16］利用测量信号与参考信号之间的相位差设计了外差式干涉仪测量滚动角误差。匡翠方等［17］基于光束的偏振状态对角度的敏感特性，利用沃拉斯顿棱镜产生两束偏振光，通过测量沃拉斯顿棱镜转动前后光强的变化实现滚动角的测量。Shi 等［18］研制了基于差动平面镜干涉法的精密滚转角测量系统，通过检测光程差或相位差变化实现滚动角的测量。但上述方法结构复杂，易受环境光与测量环境的影响。采用平行双光束［19-20］，通过测量导轨滑块不同位置处的直线度运动误差，可以间接得到滚动角误差，但此方法中双光束调平行较为困难且光束间的平行度会随时间变化。

上述针对导轨运动误差的测量均采用离线测量方法，无法准确得知导轨运动过程中的实时运动误差。本文研制了导轨六自由度运动误差实时测量系统，基于自准直原理测量滚动角误差。该测量系统结构简单，可实时测量导轨运动位姿。此外，建立了二维线性模组的空间误差模型，通过代入实时测量数据得到了二维线性模组功能点的空间运动误差。

2 原 理

二维线性模组由两根导轨在XZ平面装配而成，因六自由度测量系统体积小、模块化程度高，所以可装在二维模组的两轴中实现导轨运动误差的实时测量。该测量系统由光栅尺、四自由度运动误差测量模块和滚动角测量模块组成。其中，光栅尺测得定位误差，四自由度运动误差测量模块测得直线度误差、偏摆角及俯仰角误差，滚动角误差测量模块测得滚动角误差。图1 为单轴测量系统的安装图，光栅尺安装在导轨一侧，四自由度运动误差测量模块的激光端安装在基台上，感测端安装在滑块上，滚动角测量模块的自准直模块安装在滑块侧端，平面反射镜安装在导轨另一侧。

2.1 四自由度运动误差测量

四自由度运动误差测量模块完成直线度误差、偏摆角以及俯仰角误差测量。其中，直线度误差基于激光准直原理测得，所用传感器为位置敏感探测器（Position Sensitive Detector，PSD）（滨松公司，S5990-01，日本），如图2（a）所示；偏摆角和俯仰角误差基于激光自准直原理测得，所用传感器为四象限光电探测器（Four-quadrant Photo Detector，QPD）（First Sensor，QP10-6，德国），如图2（b）所示。

四自由度运动误差测量模块感测端跟随滑块沿导轨运动时，若导轨存在直线度误差，原本打在PSD1 中心的光斑会在Y方向和Z方向产生偏移，从而实现直线度误差的测量。直线度误差分别为：

式中Δy1，Δz1为光斑在PSD1 上的位置变化值。

QPD1 的位置预先放在聚焦透镜FL1 的焦平面上，激光端发出的光束经分光镜BS1 后通过聚焦透镜FL1 汇聚到QPD1 上。若导轨运动时有角度误差，激光会以倾斜的方式射入聚焦透镜，此时光斑在QPD1 上的位置相对于QPD1 中心会发生偏移。偏摆角εz1和俯仰角εy1为：

式中：Δx1，Δz1为光斑在QPD1 上的位置变化值；f1为聚焦透镜FL1 焦距。

2.2 滚动角误差测量

滚动角误差测量模块基于激光自准直原理测得滚动角误差，所用传感器为QPD（First Sensor，QP10-6，德国）。

如图3 所示，激光器发出光束经分光棱镜BS2 后一分为二，透射光射入固定在导轨上的平面反射镜，反射光束再次经过分光棱镜BS2，经聚焦透镜FL2 后入射光电探测器QPD2。若导轨运动时存在滚动角误差εx，则经平面反射镜反射回的光束角度会有变化，光斑在QPD2 上的位置在相对于QPD2 的中心在Z方向上发生偏移。此时通过计算光斑在QPD2 的位置变化可得到滚动角误差。滚动角误差为：

式中：Δz2为光斑在QPD2 上的位置变化值；f2为聚焦透镜FL2 的焦距。

二维线性模组总成见图4。其中，六自由度测量系统先安装在单轴中，之后再将两轴装配在XZ平面内。

图4 二维线性模组总成Fig.4 Two-dimensional linear module assembly

3 二维模组误差模型

以往对于二维线性模组的空间运动误差，直接利用光栅尺测出每轴位置，进而求解功能点的空间位置，但这种方法未考虑测量时各位置其他误差对测量的影响。本文将搭建的六自由度运动误差测量系统装在二维线性模组中，可对二维线性模组的位姿误差进行实时测量，并根据提出的空间误差模型确定二维线性模组功能点的空间位置。相较于传统方法，测量结果更加准确。

在实际测量中，导轨存在制造误差，导致二维线性模组运动过程中的实际运动位姿与理想运动位姿存在偏差。而二维线性模组整体上可看作两根导轨的组合，其几何误差可看成两个单根导轨的误差加上两根导轨之间的垂直度误差。故二维线性模组的几何误差共有13 项，如表1所示。

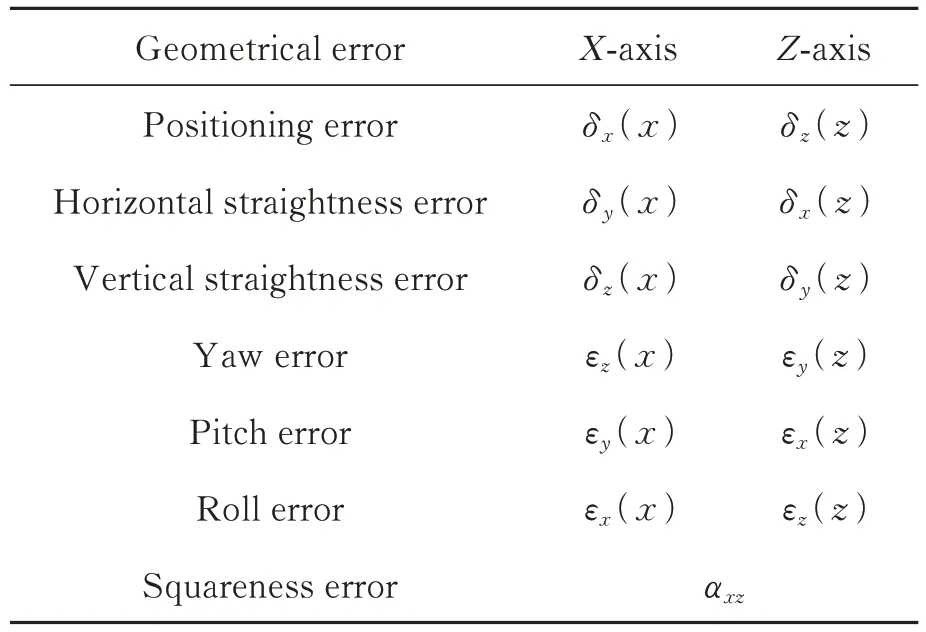
表1 二维线性模组的误差表达式Tab.1 Error expression of two-dimensional linear module

本文基于齐次坐标转换矩阵（Homogeneous Transformation Matrix，HTM）原理对二维线性模组进行空间误差建模。HTM 原理是基于刚体运动学中的多体理论，使用低序体阵列来描述空间位置关系的一种建模理论。其核心思路是对每个运动轴建立局部坐标系，根据齐次坐标变换，将各个坐标系下的运动误差转换到同一个基坐标系中进行分析。首先，依照多体理论和低序体阵列法［21］，假设二维线性模组中的X，Z运动轴和Z轴滑块为存在相对运动的低序体，并进行编号。其中，X轴为体0，Z轴为体1，Z轴上滑块为体2，并在各低序体内预设一个固连坐标系。如图5 所示，体0 坐标系O-XYZ（即二维线性模组的绝对坐标系）设置在X轴电机处的丝杠上，体1坐标系O-X1Y1Z1设置在X轴滑块中心下方的丝杠上，体2 坐标系O-X2Y2Z2设置在Z轴滑块中心下方的丝杠上，P点为Z轴滑块上的一个点。然后，通过相邻低序体进行坐标转换，将P点在体2坐标系内的相对坐标转换到体0 坐标系中，最后通过齐次坐标矩阵运算可得到P点的空间误差。

图5 二维线性模组及低序体坐标系设置Fig.5 Setting of two-dimensional linear module and loworder volume coordinate system

本文基于HTM 原理推导了二维线性模组的空间误差模型，因此，其几何误差测量点必须处于同一位置。将测量数据代入误差模型前，应先使用阿贝原则和布莱恩原则对所测数据进行转换，即将测量点（光栅尺读数头和PSD）处的误差值转换到X，Z轴上的功能点FP1 和FP2 上［22］。如图6 所示，在每个轴上，将光栅尺读数头点定义为阿贝点，直线度误差测量点（PSD 上的点）定义为布莱恩点。在二维线性模组空间误差测量中，基于阿贝-布莱恩原则进行的误差转换。X轴上各传感器测得的定位误差和直线度误差经阿贝-布莱恩原则处理后有：

图6 基于阿贝-布莱恩原则的误差转换图Fig.6 Error conversion diagram based on abbe-bryan principle

同理对Z轴处理后的误差如下：

其中：δx(x)，δz(z)分别为X，Z轴光栅尺读数头处测量的定位误差，δy(x)，δz(x)和δy(z)，δx(z)分别为X，Z轴PSD 处测量的直线度误差；δx(x)，δz(z)标记的为阿贝-布莱恩原则处理后的误差值；Laz(x)，Lay(x)和Lbx(x)，Lby(x)，Lbz( )x分别为X轴上的阿贝偏位和布莱恩偏位，Lax( )z，Lay(z)和Lbx(z)，Lby(z)，Lbz(z) 分别为Z轴上的阿贝偏位和布莱恩偏位，这里Lbx(x)和Lbz(z)的值为0。

在计算二维线性模组空间误差时，用理想运动矩阵表示导轨的理论运动值，误差特征矩阵表示导轨运动时的几何误差，如下：

其中：T01，T02分别为体0 到体1，体1 到体2 的理想运动矩阵，ΔT01，ΔT02为对应的误差特征，xm和zm分别为滑块在X，Z方向的运动距离，z0为Z方向上的初始偏移距离。

假设P点在体2 坐标系O-X2Y2Z2中的齐次坐标为P2(0，-y2，0，1)，则通过齐次坐标矩阵运算后P点在体0 坐标系中的齐次坐标为：

不考虑运动误差时P点在体0 坐标系中的齐次坐标为P0(xm，-y2，z0+zm，1)，故由二维线性模组13 项几何误差引起的P点的空间误差为：

4 实 验

4.1 标定实验

4.1.1 直线度测量传感器灵敏度标定

使用电感测微仪（型号为Mahr1240，分辨率为0.01 μm）对直线度测量传感器（PSD）进行灵敏度标定［23］。实验结果表明，在传感器±100 μm的量程内，直线度误差灵敏度的标定残差均小于±1μm。

4.1.2 角度测量传感器灵敏度标定

使用光电自准直仪（AutoMAT5000U 型，分辨率为0.01′）对角度测量传感器（QPD）的灵敏度进行标定［23］。实验结果表明：在传感器±100′′的量程内，偏摆角和俯仰角的标定残差均小于±1′。

由图2 可知，滚动角测量模块中的传感器也为QPD，其灵敏度标定方法与上述一致。

4.1.3 平面反射镜误差标定

由于平面反射镜存在制造误差，反射镜表面质量不均匀，进而会对滚动角测量造成影响，因此，测量前需要先标定平面反射镜的系统误差。标定设备架设如图7（a）所示，滑块沿X向移动时，在位置i处，滚动角测量模块与水平仪同时对滚动角进行测量。以水平仪测量的滚动角εlevel(i)为基准，模块测量值ε′x(i)与水平仪测量的残差即为位置i处平面反射镜的系统误差εerror(i)，如下：

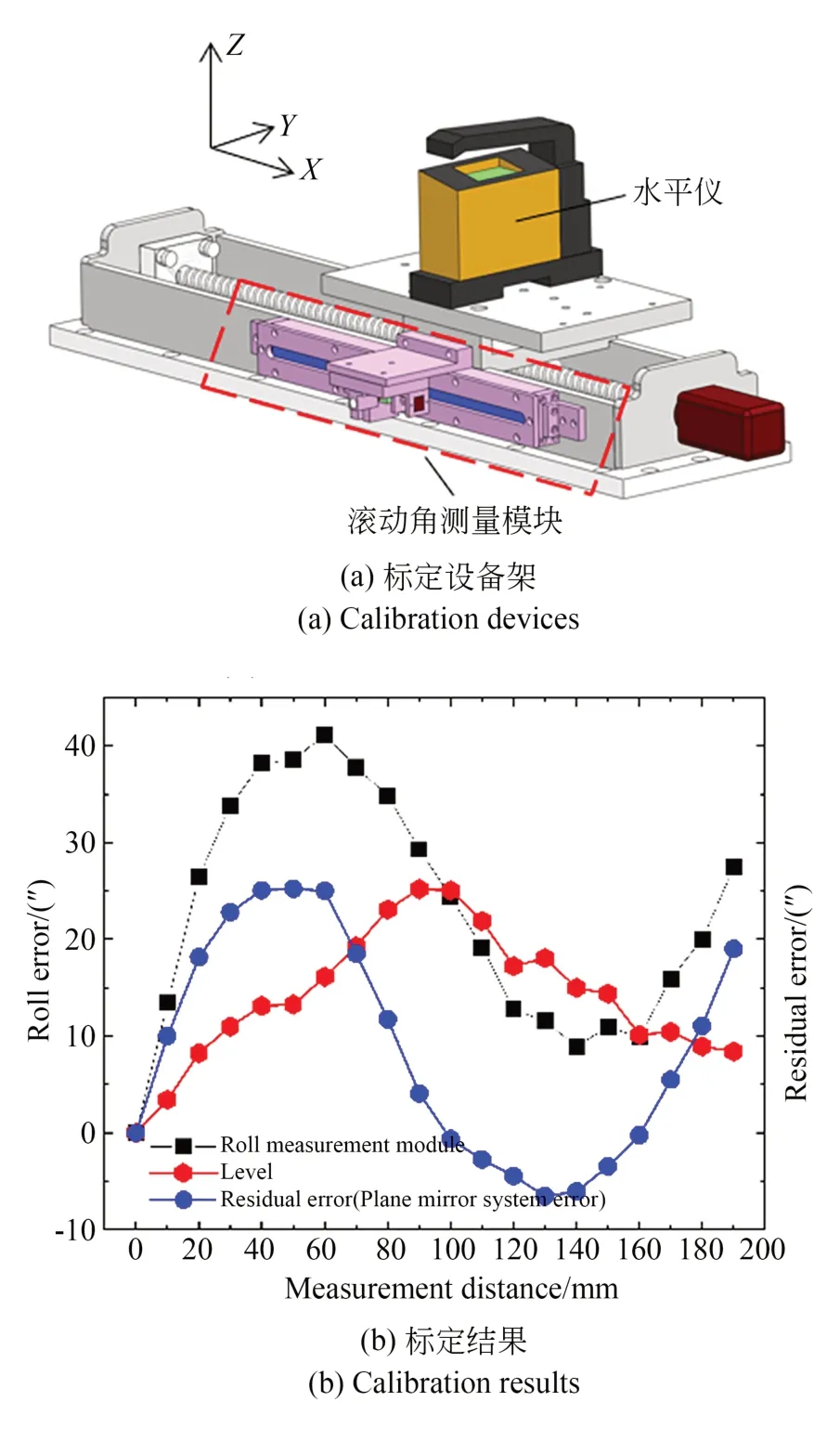
图7 平面反射镜误差标定Fig.7 Error calibration of plane mirror system

测量数据εerror(i)为散点值，因此对它进行拟合处理，得到平面反射镜在测量范围内各位置的误差。标定结果如图7（b）所示。

在测量出平面镜系统误差后，使用本测量模块进行其他导轨滚动角测量时，直接测量得到数值ε′x(i)后，可通过式（12）进行补偿，求解出任意位置i处导轨的实际滚动角误差εx(i)。

4.2 精度比对实验

4.2.1 定位误差比对

本文使用激光干涉仪（美国光动MCV-500型，分辨率为1 nm）和光栅尺完成定位误差的比对实验。然而，MCV-500 的测量光线与光栅尺读数头的运动轴线存在偏位，因此，需要通过阿贝原理将激光干涉仪的测量值转换到光栅尺后再与光栅尺所测数据进行比对。数据处理参照式（4）和式（5）中的定位误差公式。

按图8（a）架设实验设备。实验时，角耦棱镜与光栅尺读数头跟随滑块在X轴0～190 mm 内运动，记录各位置激光干涉仪与光栅尺的值。比对结果如图8（b）所示，在0～190 mm 内，X轴定位误差的比对残差为±1 μm。

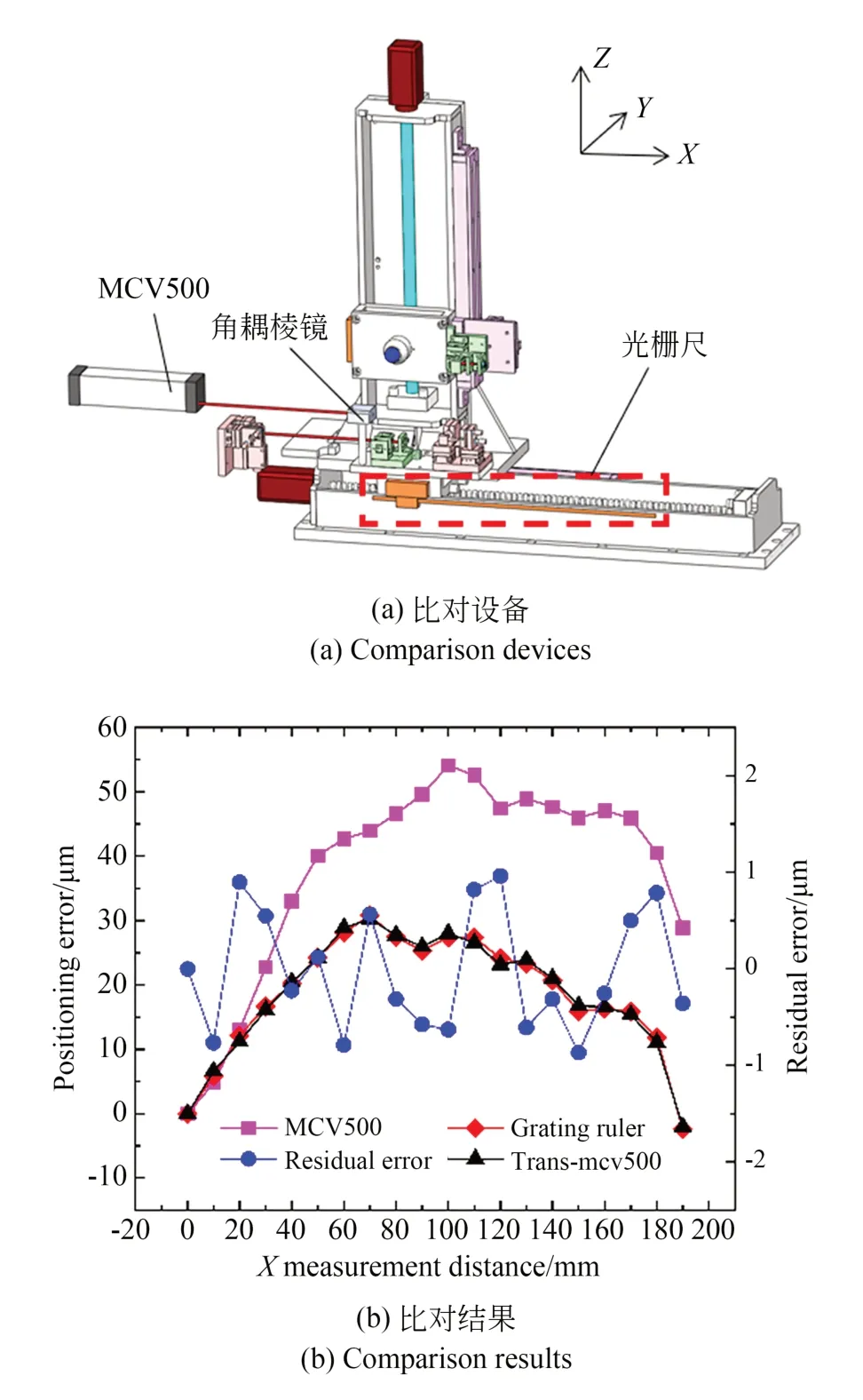
图8 X 轴定位误差比对Fig.8 Comparison of X axial positioning error

同理，按图9（a）架设实验设备，可对Z轴定位误差进行比对，结果如图9（b）所示，在0～190 mm内Z轴定位误差的比对残差为±1.2 μm。

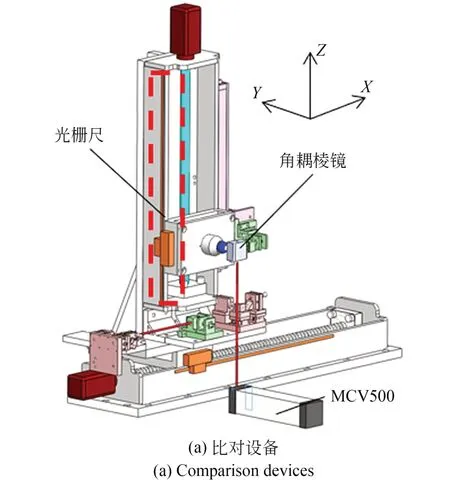
图9 Z 轴定位误差比对Fig.9 Comparison of Z axial positioning error

4.2.2 直线度误差比对

本文使用电感测微仪搭配大理石平尺（精度等级为00，平面度误差为3 μm）和PSD 完成直线度误差的比对实验。但电感测头的运动轨迹与PSD 测量光线存在偏位，因此，需要通过布莱恩原理将电感测头的测量值转换到PSD 处后再与PSD 所测数据进行比对。数据处理参照式（4）和式（5）中的直线度误差公式。

按图10 架设实验设备，将电感测头打在固定在光学平台上的大理石平尺上。实验时，电感测头随水平轴滑块在测量范围内移动，记录各位置电感测头与PSD1 传感器在Y，Z方向的值。比对结果如图11 所示，在0～190 mm 内X轴Y方向直线度比对残差为±1.3 μm，Z方向直线度比对残差为±1.3 μm。

图10 X 轴直线度比对设备Fig.10 Devices for comparison of X axial straightness error

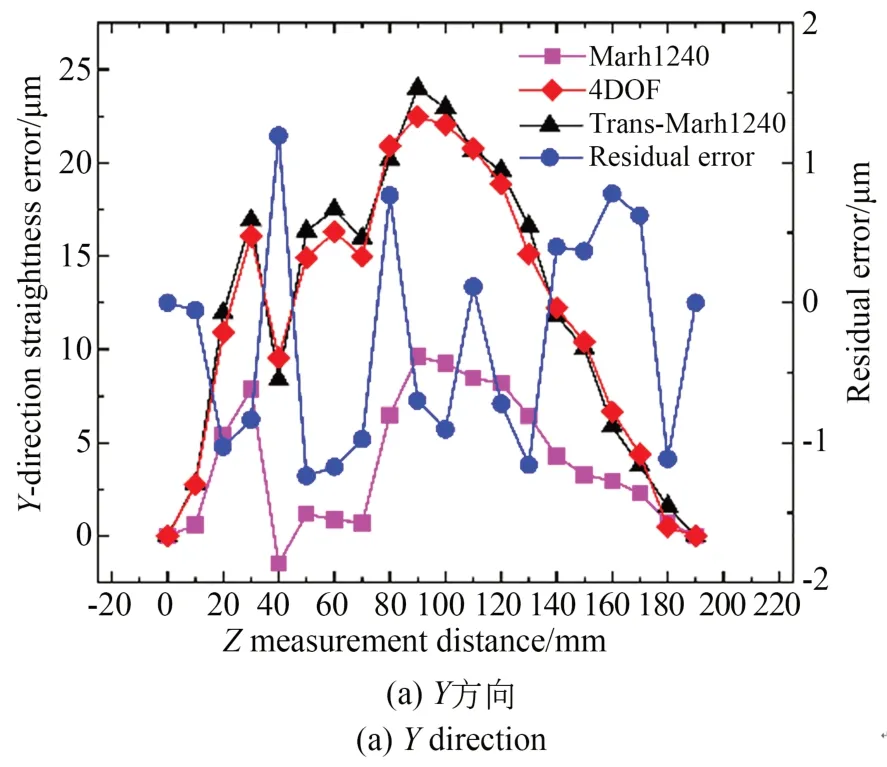
图11 X 轴直线度比对结果Fig.11 Comparison results of X axial straightness error

同理，按图12 固定测头，利用大理石方尺（精度等级为0，平面度误差为3 μm）完成Z轴直线度误差动态比对。比对结果如图13 所示，在0～190 mm内Z轴X方向直线度的比对残差为±1 μm，Y方向直线度的比对残差为±0.8 μm。

图12 Z 轴直线度比对设备Fig.12 Devices for comparison of Z axial straightness error

图13 Z 轴直线度比对结果Fig.13 Comparison results of Z axial straightness error

4.2.3 轴系姿态角度测量比对

4.2.3.1 偏摆角、俯仰角误差比对

按图14 所示架设实验设备。实验时，四自由度运动误差测量模块激光端固定，感测端与靶镜跟随滑块在测量范围内运动，记录光电自准直仪与四自由度运动误差测量模块的偏摆角与俯仰角的值。比对结果如图15 所示，在0～190 mm 内X轴偏摆角与俯仰角的比对残差均为±1′。

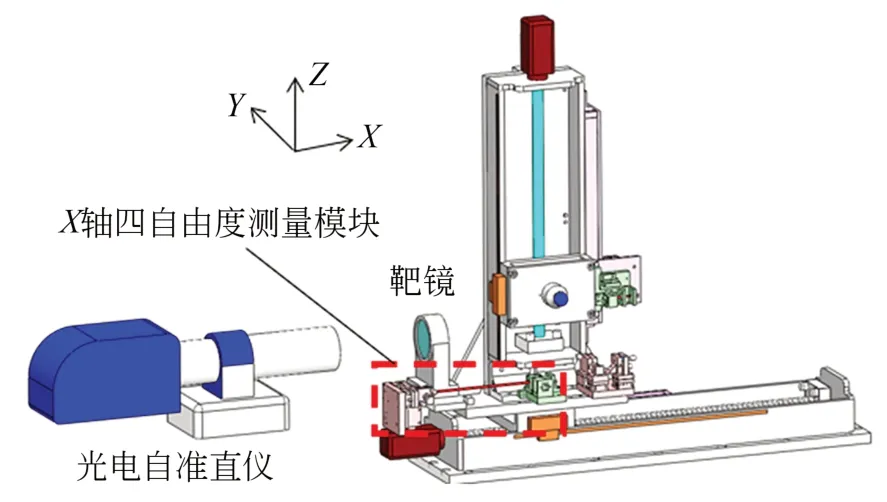
图14 X 轴偏摆角、俯仰角比对设备Fig.14 Device for comparison of X axial angular errors

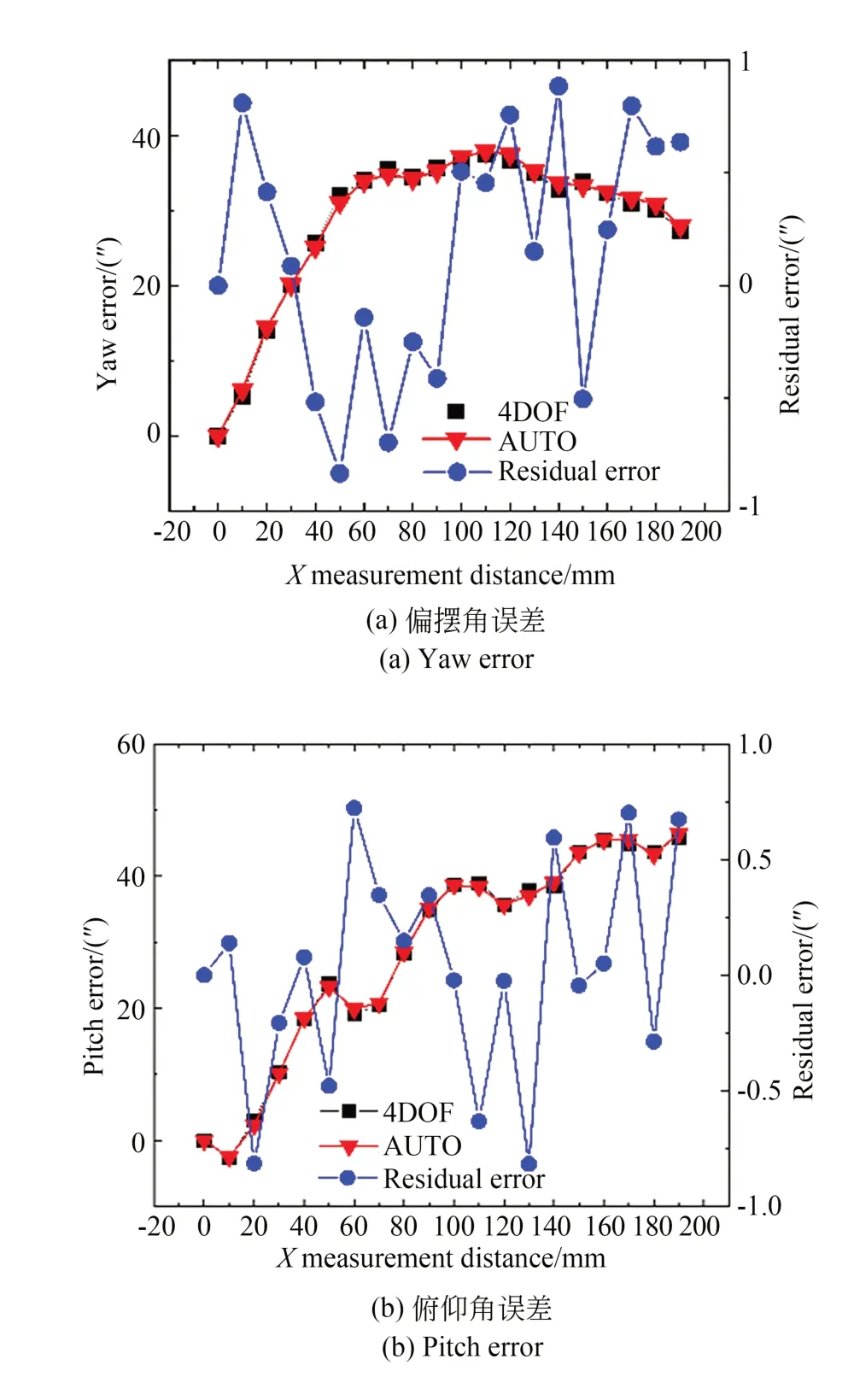
图15 X 轴角度误差比对结果Fig.15 Comparison results of X axial angular errors

同理，按图16 架设实验设备，将靶镜换装在Z轴滑块上，借助Z轴四自由度运动误差测量系统完成偏摆角、俯仰角的误差比对。比对结果如图17 所示，在0～190 mm 内Z轴偏摆角与俯仰角的比对残差均为±1.5′。

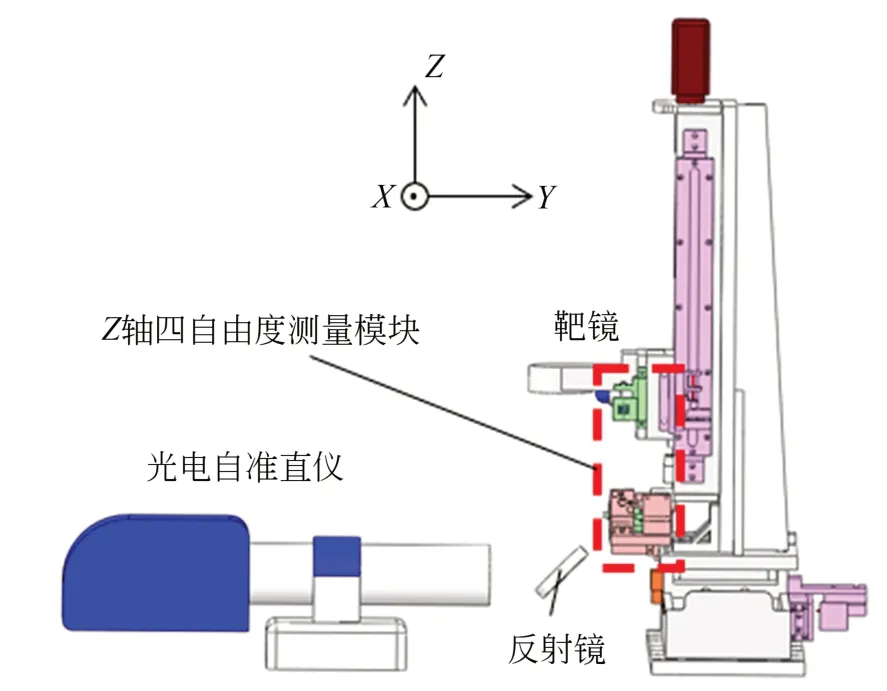
图16 Z 轴角度比对设备架设Fig.16 Device for comparison of Z axial angular errors

图17 Z 轴角度误差比对结果Fig.17 Comparison results of Z axial angular errors

4.2.3.2 滚动角误差比对

按图18（a）架设实验设备。实验时，平面反射镜固定在导轨侧面，滚动角测量模块与水平仪（青岛前哨WLL11 型，分辨率为0.2′′）跟随滑块在测量范围内运动，记录各位置水平仪示数与滚动角测量模块所测示数。比对结果如图18（b）所示，在0～190 mm 内X轴滚动角的比对残差在±1′以内。

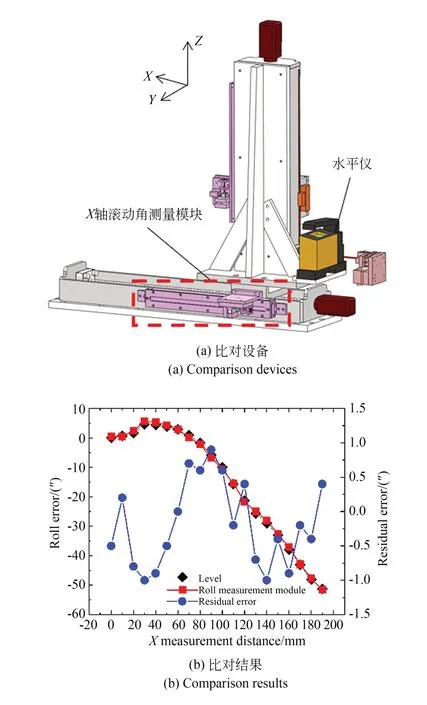
图18 X 轴滚动角比对Fig.18 Comparison of X axial roll error

按图19（a）架设实验设备，电感测头A，B 打在大理石方尺同一表面，记录各位置电感测头示数的差值与滚动角测量模块的示数进行比对。比对结果如图19（b）所示，在0～190 mm 内Z轴滚动角的比对残差在±1′′以内。

5 空间误差测量比对实验

由式（6）可知，二维线性模组空间误差模型求解中需要垂直度误差，因此需要进行垂直度测量［24］。经5 次测量，二维线性模组的垂直度误差为-42.4′′，标准差为0.45′；大理石方尺的垂直度误差为8.18′′，标准差为0.18′′。

为实现二维线性模组的误差实时测量，本文对图20 所示的工作平面（XZ平面，190 mm×190 mm 正方形）的对角线位置进行测量，并与激光干涉仪（MCV-500）所测位置值进行比对。在该对角线上选取19 个等间距点（P1～P19）进行比对。

按图21 架设实验设备，实验时，X轴与Z轴均从起始位置间隔10 mm 沿正方向运动，记录激光干涉仪的数值。记公式（10）求出的空间误差E的坐标为(xe，ye，ze)，根据式（13）将测量系统测出数据代入误差模型后求解的对角线值与MCV-500 测出的对角线值进行比较，即：

式中：EBD和EAD分别为使用误差模型前后计算出的XZ平面对角线位置的测量误差，PMCV为MCV500 测出的XZ平面对角线位置的测量误差。测量结果如图22 所示，使用二维线性模组空间误差模型求解前后，XZ平面对角线位置的测量误差值由68 μm 降至13 μm，说明该系统能够有效地测量线性模组误差。

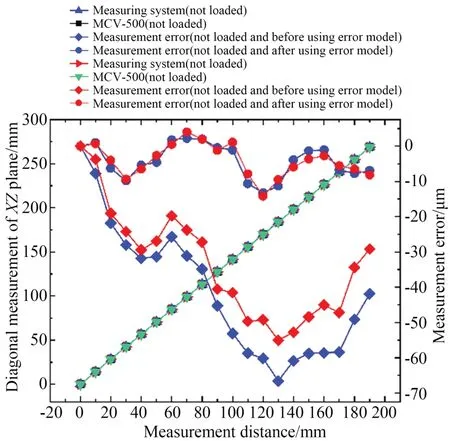
图22 XZ 平面对角线位置测量误差比对Fig.22 Comparison of diagonal position measurement error of XZ plane

上述实验均在空载状态下进行。由于在加载状态下二维线性模组各位置的运动误差会发生变化，为验证测量系统能够实时测量线性模组的空间误差变化，在Z轴滑块上加装质量为2 kg 的标准砝码作为对照组实验。加载实验测量结果如图22 所示，使用二维线性模组空间误差模型求解前后，XZ平面对角线位置的测量误差由56 μm 降至14 μm，该误差测量系统能够实现实时测量。

6 结 论

为测量二维线性模组的运动误差，本文搭建了由光栅尺、四自由度运动误差测量模块和滚动角误差测量模块组成的误差实时测量系统，基于HTM 原理构建二维模组空间误差模型，完成测量系统标定和比对实验。最终，误差实时测量系统的定位误差、直线度误差和角度误差分别达到±1.2 μm，±1.3 μm 和±1″。根据所提出的空间误差模型分析二维线性模组XZ平面对角线位置的测量误差。结果表明，使用二维线性模组空间误差模型求解前后，XZ平面对角线位置的测量误差由68 μm 降至13 μm。此外，在加载状态下进行线性模组的空间误差测量，在Z轴滑块上加装质量为2 kg 的标准砝码进行对照实验。结果显示，在使用二维线性模组空间误差模型求解前后，XZ平面对角线位置的测量误差由56 μm 降至14 μm。由此表明，该系统能够实现线性模组误差的实时测量。