Low-lying electronic states of osmium monoxide OsO

Wen Yan(严汶) and Wenli Zou(邹文利),†

1Institute of Modern Physics,Northwest University,Xi’an 710127,China

2Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China

Keywords: transition dipole moment, multi-reference second-order perturbation theory, spin–orbit coupling,exact two-component

1.Introduction

Transition metal-containing small molecules are known to pose challenges to spectral assignments.In addition to the strong spin–orbit coupling (SOC) effects, the abundance electronic configurations, the dense distribution of electronic states, and the high angular quantum numbers make the assignment of electronic spectra rather complicated.In this respect, the high-precision theoretical calculations by multireference methods play crucial roles in assisting experimental assignments.However, the multi-reference methods are not black-box tools,which hinders their widespread applications.In a recent paper[1]we studied the low-lying electronic states of the osmium monoxide cation (OsO+), and in the present work,we focus on the neutral OsO molecule because its emission spectra measured nearly 40 years ago[2]have not been assigned until now.

Both experimental and theoretical studies of OsO are scarce.Gattereret al.[3]and Raziunaset al.[4]reported the earliest emission spectra of OsO in 1957 and in 1965, respectively, but no analyses were made.Weltner suggested a possible ground state5Σ in a review published in 1978.[5]In 1984,Balfour and Ram[2]photographed the emission spectra of OsO in the region 405 nm–875 nm, in which many bands had been observed.However, they could not determine the spectral term of the ground state.The candidate ground states of OsO were theoretically studied only at the density functional theory (DFT) level of theory without considering the SOC effects, which could be either3Φ or5Σ+depending on the functionals.[6–8]Due to the fact that the first-order SOC constant of5Σ+is zero,one may speculate that the ground Ωstate of OsO comes probably from3Φ.However, this is not true according to our results in this study.On the whole, the ground state and the assignments of the experimental emission bands of OsO are still not known.

This paper is structured as follows.Some computational details are given first.In the subsequent section, the lowlying Λ–S and Ω states of OsO have been studied by highprecision multi-reference calculations, which are used to assign the emission bands.Important findings of this work are summarized in the Conclusion section.

2.Theoretical method

The scalar relativistic effects are taken into account via the exact two-component(X2C)Hamiltonian,[9,10]which is combined with the relativistically contracted 4-ζquality ANO-R3 basis set[11,12]and the finite size nuclear model.Totally 43 low-lying Λ–S states of OsO below 3×104cm-1are calculated using SA-CASSCF (state-averaged complete active space self-consistent field)with theC2vpoint group symmetry, including fourteen singlet, twenty triplet, eight quintet, and one septet ones (see Table 1).Based on the SACASSCF wavefunctions, two multi-reference methods have been used in this study to take dynamic correlations into account,i.e.,RMS-CASPT2(rotated multi-state complete active space second-order perturbation theory)[13]and MS-NEVPT2(multi-state partially contractedn-electron valence state second order perturbation theory).[14]The active space consists of 12 electrons in 9 molecular orbitals(MOs),i.e.CAS(12e,9o),corresponding to the 5d6s shells of Os and the 2p shell of O.All the occupied MOs below the active space are relaxed in the SA-CASSCF calculations,whereas in the RMS-CASPT2 and MS-NEVPT2 calculations the 24 electrons in the MOs corresponding to O 2s and semi-core shells Os 4f5s5p are also correlated.The resulted total number of configurations for singlet, triplet, and quintet states are approximately 9×109,18×109, and 3×109, respectively.Since CASPT2 suffers from the intruder state problem,an imaginary level shift[15]of 0.25 a.u.(atomic unit)and an IPEA level shift[16]of 0.25 a.u.are used together, which lead to the weights of the reference states being about 81%.

The SOC effects are considered via the biorthonormal state-interaction (SI) approach[17]with the one-center atomic mean field integral (AMFI) approximation[18]for one- and two-electron spin–orbit integrals.The perturbatively modified CASSCF (PM-CASSCF) wavefunctions by RMS-CASPT2 are adopted to construct the spin–orbit matrix, where the diagonal elements are replaced by the corresponding RMSCASPT2 or MS-NEVPT2 energies calculated above.More technical details about SOC calculations may be found in Ref.[19].

The BDF quantum chemistry program package[20]is used for the quadratically convergent SA-CASSCF calculations,whereas the MS-NEVPT2 calculations are carried out using the Xi’an-CI program package[21]that interfaces with BDF.The transformed SA-CASSCF wavefunctions are also passed to the OpenMolcas program package[22,23]to perform the RMS-CASPT2 and subsequent SI calculations.Since the double group symmetry is not implemented in the SI approach of OpenMolcas, the in-house Fortran90 program OmSym-II is used to identify the Ω states.Based on the potential energy curves(PECs)of Λ–S or Ω states,the spectroscopic constants are fitted by numerically solving the one-dimensional Schr¨odinger equation using Le Roy’s LEVEL program,[24]including the adiabatic excitation energy (Te), the equilibrium bond length(Re),the vibrational frequency(ωe),and the rotational constant(Be).

3.Results and discussion

3.1.Λ–S states of OsO

The PECs of the Λ–S states by MS-NEVPT2 are plotted in Fig.1.The fitted spectroscopic constants are collected in Table 1,and are compared with the ones by RMS-CASPT2.

Both the RMS-CASPT2 and MS-NEVPT2 results show that the ground Λ–S state of OsO is the closed-shell [1]1Σ+whereas the first excited state [1]3Π is only one or two hundred wavenumbers higher in energy, thus the other candidate ground states [1]3Φ and [1]5Σ+in early DFT studies[6–8]are completely denied.The excitation energies of the higher Λ–S states by RMS-CASPT2 and MS-NEVPT2 are basically coincident, but the energy differences can be 0.2 eV (about 1600 cm-1)or even larger in some states,for example,[1]3Φ and[1]5Σ+.To verify those inconsistent results,the more accurate SDSCI+P (static-dynamic-static multi-reference configuration interaction with Pople’s cluster corrections)[25,26]calculations are performed at the bond distance of 1.66 ˚A with the same active space and frozen core electrons, and the results compare well with the MS-NEVPT2 ones with the maximum error of about 500 cm-1.By comparisons, the RMSCASPT2 underestimates the energies of [1]3Φ and [1]5Σ+by about 800 cm-1and 2200 cm-1, respectively.Consequently,only the MS-NEVPT2/SI results are reported in the following subsection.

a (A)RMS-CASPT2;(B)MS-NEVPT2.b 1σ: O 2pσ,2σ: Os 5dσ6s,3σ: Os 5dσ6s+O 2pσ,1π: O 2pπ+Os 5dπ,2π: Os 5dπ+O 2pπ,1δ: Os 5dδ.

Using the SA-CASSCF wavefunctions,the Wiberg bond indices (WBIs) in the NAO (natural atomic orbital) basis[27]are calculated for the lowest five Λ–S states below 3000 cm-1.It is found that the OsO molecule has a double bond in[1]1Σ+(WBI=1.9), a one and a half bond in [1]3Π and[1]3Φ (WBI=1.5), and a single bond in [1]5Σ+and [1]5∆(WBI=1.2).The bond strengthnis also reflected in the equilibrium bond length through an approximate Badger relationshipn=|a|r-|b|e(although there are some counter examples in the literatures[28,29]).Among the lowest five Λ-S states,the bond orders may be confirmed further by the qualitatively consistent bond lengths: [1]1Σ+has the shortest bond length of about 1.60 ˚A, [1]3Π and [1]3Φ present the medium bond length of about 1.66 ˚A, whereas the longest bond length of about 1.70 ˚A exists in the two quintet states[1]5Σ+and[1]5∆.

3.2.Ω states of OsO

At the MS-NEVPT2/SI level of theory, the PECs of the low-lying Ω states below 2.5×104cm-1are shown in Fig.2,and the spectroscopic constants are summarized in Table 2.The Ω states higher than 2.5×104cm-1are expected to be unreliable due to insufficient auxiliary Λ–S states in the spin–orbit matrix and therefore are not reported.

Fig.2.The PECs of low-lying Ω states of OsO by MS-NEVPT2/SI.

After including SOC,the lowest five Λ–S states aforementioned lead to the fifteen Ω states below 9×103cm-1(i.e.{1-3}0+,{1}0-,{1-3}1,{1-4}2,{1-2}3,and{1-2}4)as well as two additional Ω states{2-3}0-.Since the ground Λ–S state[1]1Σ+does not split,the Ω=2 branch of the first excited Λ–S state[1]3Π becomes the ground Ω state.Accordingly the bond order of OsO in its ground state decreases from a double bond to a one and a half bond.In addition to{1}2,the[1]3Π state also splits into the first Ω=0+, 0-, and 1 sub-states, but in the former two sub-states some of the other Λ–S states also make significant contributions.

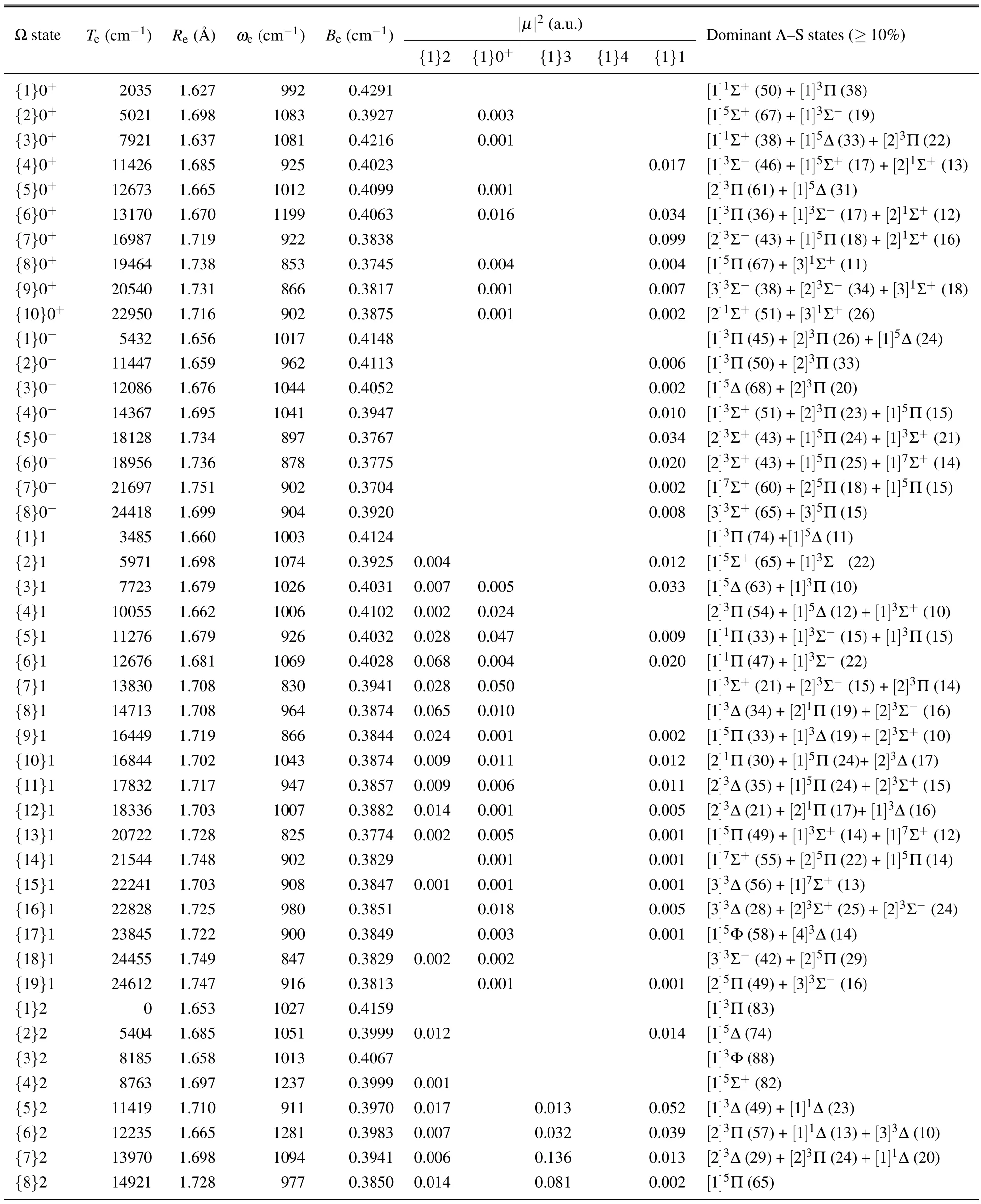
Table 2.Spectroscopic constants of Ω states of 192Os16O by MS-NEVPT2/SI.

{9}2 16683 1.714 926 0.3856 0.012 0.002 0.160 [2]3∆(27)+[1]3∆(25)+[1]1∆(23){10}2 20879 1.748 842 0.3744 0.032 0.021 [1]7Σ+ (45)+[2]5Π(25)+[4]3∆(12){11}2 21417 1.727 985 0.3791 0.007 0.005 0.007 [1]5Φ(46)+[4]3∆(11)+[1]7Σ+ (10){12}2 22412 1.704 923 0.3844 0.001 0.017 [3]3∆(59)+[1]1∆(17){13}2 23087 1.730 898 0.3817 0.012 0.008 0.002 [2]1∆(47)+[3]1∆(10){14}2 24299 1.722 823 0.3835 0.002 0.009 0.046 [2]5Π(49)+[1]7Σ+ (15)+[4]3∆(11){15}2 24365 1.740 915 0.3783 0.013 [4]3∆(40)+[5]3∆(12)+[1]5Φ(12){1}3 2459 1.676 969 0.4048 0.009 [1]3Φ(41)+[1]5∆(23)+[1]1Φ(15){2}3 4972 1.674 1067 0.4056 0.015 0.081 [1]5∆(58)+[1]3Φ(24){3}3 9802 1.705 951 0.3885 0.167 0.001 0.037 [1]3∆(52)+[1]5Π(17)+[1]5∆(14){4}3 13566 1.723 900 0.3805 0.111 0.035 0.010 [1]5Π(56)+[1]3∆(18)+[2]3∆(12){5}3 14635 1.666 1223 0.3924 0.068 0.005 0.006 [1]1Φ(57)+[1]3Φ(20){6}3 16531 1.721 920 0.3837 0.011 0.002 0.148 [2]3∆(59)+[1]1Φ(16){7}3 17606 1.711.724.733 976 0.3919 0.004 0.004 [1]3Γ(77){8}3 19139 1870 0.3834 0.023 0.006 0.027 [3]3∆(65)+[4]3∆(11){9}3 19793 1881 0.3782 0.024 0.001 0.020 [4]3∆(26)+[1]5Φ(22)+[1]7Σ+ (18){10}3 20791 1.737 897 0.3776 0.002 0.003 [1]5Φ(29)+[1]7Σ+ (28)+[2]5Π(20){11}3 21501 1.719 992 0.3842 0.008 [2]3Γ(54)+[2]5Π(10)+[1]7Σ+ (10){12}3 22746 1.718 939 0.3900 0.007 0.002 [4]3∆(36)+[1]5Φ(29)+[2]3Γ(17){13}3 24464 1.764 742 0.3682 0.016 0.001 [2]5Π(54)+[1]7Σ+ (36){1}4 3298 1.680 1024 0.4025 [1]5∆(72)+[1]3Φ(26){2}4 5709 1.667 1037 0.4084 0.076 [1]3Φ(62)+[1]5∆(33){3}4 13873 1.713 958 0.3879 0.098 0.006 [1]3Γ(86){4}4 19214 1.706 939 0.3879 0.050 [2]3Γ(70)+[1]1Γ(20){5}4 20424 1.732 896 0.3803 0.005 [1]5Φ(68)+[2]3Φ(19){6}4 24416 1.710 913 0.3895 0.003 0.001 [1]1Γ(69)+[2]3Γ(23){1}5 10860 1.717 940 0.3848 0.078 [1]3Γ(91){2}5 20230 1.714 898 0.3853 0.033 [2]3Γ(84)+[1]5Φ(12){3}5 21408 1.732 886 0.3804 0.019 [1]5Φ(75)+[2]3Γ(21){1}6 23848 1.723 926 0.3842 [1]1I(100)

The dominant components of the higher Ω states are more complicated duo to strong SOC effects,and there is not a dominant Λ–S component with the weight lager than 70%except for{7}3 and Ω = 4,5, and 6 states.Considering the lack of reliable experimental spectroscopic constants for comparison, we will discuss them below combined with the assignment of the experimental emission bands.However, due to the high density of Ω states distributed in the energy range of 1.5×104cm-1–2.5×104cm-1,it is a tough work to identify the experimental emission bands as the calculated upper and lower Ω states.Transition probability is a necessary indicator to distinguish the allowed transitions by selection rule.At 1.66 ˚A, the squares of total transition dipole moments (|µ|2)between the lowest five({1}2,{1}3,{1}0+,{1}4,and{1}1)and the higher excited Ω states are listed in Table 2, which are proportional to the absorption intensity via the relationshipIabs∝N′′∆e|µ|2withN′′being the population on the lower Ωstate due to Boltzmann distribution[30]and∆ebeing the energy difference between two Ω states.Similarly the emission intensity isIems∝N′∆4e|µ|2whereN′is the population on the upper state depending on experimental conditions as well as radiative and nonradiative processes.[30]For a given wavelength range,∆emay be looked on as a constant, and thereforeIabs(Iems)depends mainly onN′′(N′) and|µ|2.For emission intensity,however,the absolute value of|µ|2is not significant due to the uncertainty ofN′,unless two emissions come from a common upper Ω state.

Seven emission bands of OsO have been recorded experimentally by Balfour and Ram,[2]called the 449-nm,455-nm,513-nm,614-nm,754-nm,825-nm,and 874-nm systems,respectively, according to the wavelengths (cf.Table I in Ref.[2]), but none of them were assigned.In Table 3, we make preliminary assignments for the(0,0)band heads.

In the 449-nm system with ∆Ω = 0, Balfour and Ram speculated the lower state to be the ground Ω state of OsO,[2]which has a rotational constant of 0.4023 cm-1and a bond length of 1.685 ˚A.However,in our theoretical results of{1}2,the rotational constant is 0.0136 cm-1larger whereas the bond length is 0.032 ˚A shorter(see Table 2),exceeding the expected error range of theoretical calculations.Therefore, the lower state should be the other Ω states.In fact,{1}3 and{1}4 are good candidates with consistent rotational constants and bond lengths.With the aid of the quite small rotational constant(B0)of 0.3657 cm-1,the upper state of the emission band may be easily assigned as{13}3, and the lower state must be{1}3 because of ∆Ω=0.However, the transition dipole moment of{13}3-{1}3 is very small,showing the complexity in the transition mechanism.

Table 3.Assignment of experimental emission bands of 192Os16O a.

a Values in parentheses in the Te,ωe,and Be columns are the experimental T0,∆G1/2,and B0,respectively,from Ref.[2].b Estimated from the 513-nm band system.[2]

The 825-nm system with ∆Ω=±1 has the same lower state as in the above 449-nm system,[2]i.e.{1}3.According to the experimental excitation energy of 12119 cm-1and the rotational constant (B0) of 0.3845 cm-1, the upper state may be assigned as{8}2,which comes mainly from[1]5Π.

In the 455-,513-,and 874-nm systems,nothing is known except excitation energies and ∆Ω=0.The allowed candidate transitions are{19}1→{1}1,{12}2→{1}2, and{6}4→{1}4 for the 455-nm band system.The other possible transitions are{16}1→{1}1 and{12}3→{1}3 for the 513-nm system,and{6}0+→{1}0+,{5}2→{1}2,and{4}3→{1}3 for the 874-nm system.The{8}1→{1}1 transition lies also in the region 874 nm but it is forbidden and therefore may be excluded.

The 614-nm and 754-nm systems are the transitions with ∆Ω =±1.Due to the lack of experimental rotational constants for comparison, there are more possibilities of allowed candidate transitions.The 614-nm system may be assigned to{12}1→{1}0+,{9}0+/{10}2→{1}1,

{9}1/{10}1/{6}3→{1}2,{4}4→{1}3, or{9}3/{2}5→{1}4, whereas the 754-nm system can be{7}0+/{9}2→{1}1 or{6}1/{7}1/{4}3→{1}2.

4.Conclusion

In this paper,the potential energy curves of low-lying Λ–S states of OsO have been calculated by X2C/MS-NEVPT2,and the fitted spectroscopic constants are compared with the ones by X2C/RMS-CASPT2 and the more accurate X2C/SDSCI+P.The SOC effects are also considered via X2C/MS-NEVPT2/SI to get Ω states.Roos and Malmqvist[19]have shown that the scalar relativistic multi-reference perturbation theory plus SI is applicable to not onlyd-block elements but also actinides, and therefore may be the most feasible scheme for studying the electronic spectra of uranium monoxide.[31]

Theoretical results show that the ground Λ–S and Ω states of OsO are1Σ+and3Π2, respectively.Based on the theoretical spectroscopic constants and transition dipole moments between Ω states,seven emission bands have been preliminarily assigned.Our results should be useful for guiding future measurements and assignments of near-infrared and visibleultraviolet spectra of OsO.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No.22073072) and the Double First-Class University Construction Project of Northwest University.