Oscillator strength and cross section study of the valence-shell excitations of NO2 by fast electron scattering

Qiang Sun(孙强), Jin-Feng Chen(陈锦峰), Zhi-Wei Nie(聂智伟), Jian-Hui Zhu(朱剑辉), and Lin-Fan Zhu(朱林繁)

Department of Modern Physics,University of Science and Technology of China,Hefei 230026,China

Keywords: nitrogen dioxide,oscillator strength,integral cross section,electron scattering

1.Introduction

Nitrogen dioxide(NO2)is one of the most important pollutants in the atmosphere,[1]which is difficult to remove chemically.Meanwhile, NO2has a non-negligible indirect impact on the greenhouse effect,[2,3]although it is not a greenhouse gas itself.More seriously, NO2is an important intermediate product involved in the cyclic catalytic decomposition of atmosphere ozone,thus posing a threat to the ozone shield.[4,5]In addition,NO2has attracted the attention of many theorists for its open shell structure.[6]Therefore, accurate knowledge of the oscillator strength and cross section data of NO2is vital for the fundamental research and understanding of its evolution in the earth’s atmosphere.

NO2is a paramagnetic and bent molecule belonging toC2vpoint group,and the ground state can be represented as

The electronic structure of NO2has been extensively studied, although it is very difficult to handle its dimer N2O4experimentally.Hall and Blacet[7]measured the photoabsorption spectra of NO2–N2O4mixtures in the energy range of 2.5–5.2 eV at three different pressures,and separated the contribution of NO2and N2O4using the equilibrium constant expression.[8]Nakayamaet al.[9]obtained the photoabsorption curves of NO2in the range of 4.6–11.5 eV and corrected the effects of underlying N2O4by extrapolating to zero pressure.Johnston and Graham[10]obtained the photoabsorption spectrum of NO2between 3.0 eV and 6.7 eV at low pressures (0.4–4 Pa), where the contribution of N2O4could be negligible.Similarly, the photoabsorption spectra of NO2and N2O4were measured in the energy range of 3.0–6.7 eV,and the effect of temperature on the NO2photoabsorption was reported.[11]Similar to the processing method of Hall and Blacet, Schneideret al.[12]obtained the photoabsorption cross-sections of NO2in the energy range of 1.8–6.2 eV using the equilibrium constant and compared their results with the previously published data.The photoabsorption cross sections of NO2in the 2.5–6.2 eV region were successively measured by Merienneet al.[13–16]at low pressures with a higher resolution,at ambient and low temperatures.Bogumilet al.[17]measured the photoabsorption spectrum of NO2in the 1.4–5.4 eV region,and the influence of N2O4was corrected from the measurements at three different partial pressures of NO2/N2O4.In addition to the photoabsorption method, the optical oscillator strengths densities(OOSDs),which are equivalent to the photoabsorption cross sections,were determined by the dipole(e,e)method at an incident electron energy of 3 keV.[18]Moreover,the electronic structures and spectrum of NO2were studied theoretically based on the semiempirical method[19]and the equilibrium geometry,[20]respectively.

Although the electronic structures and photoabsorption cross sections of NO2have been comprehensively studied,there remain significant differences amongst the published data,particularly between 5.2 eV and 6.3 eV.Meanwhile,the momentum transfer dependence behaviors of the valence-shell excitations of NO2, i.e., the generalized oscillator strengths(GOSs),have not been studied so far.Moreover,there are no reported differential or integral cross sections(DCSs or ICSs)of the valence-shell excitations of NO2as well.

In this work,the GOSs,DCSs and ICSs of the electronic transitions of NO2have been comprehensively studied by the high-resolution electron energy loss(EEL)spectroscopy.With the aid of the relative flow and crossed-beam techniques, the absolute GOSs can be obtained as a function related to the momentum transfer.Using the Lassettre formula,[21,22]we can obtain the analytical expressions of the measured GOSs by fitting the experimental data and the optical oscillator strengths(OOSs)correspond to the analytical GOSs at zero momentum transfer,which can cross-check the previous experimental results.The fitted curves can be further used to obtain the Born ICSs by the integration over momentum transfers.It should be noted that the Born ICSs are more reliable when the Born approximation is satisfied at high incident electron energies.[23]In contrast, the Born ICSs are usually overestimated at low incident energies, so the BE-scaling method is introduced to obtain accurate ICS data for the dipole-allowed transitions.

2.Experiment and data analysis

The high-resolution fast electron energy loss spectrometer used in this work has been introduced in detail in our previous works,[24–26]so only a brief overview is given here.The spectrometer was operated at an incident electron energy of 1.5 keV and an energy resolution of about 70 meV.In order to simplify the normalization processes and improve the accuracy of the experimental results, the premixed gas with a ratio of 1:2 of NO2and He was used in this experiment with an estimated error of less than 2%, to implement the relative flow technique.[27–30]During the experiment, the premixed gas flowed into the interaction chamber simultaneously and continuously, crossing with the incident electron beam at an angle of 90◦.The background pressure before the measurements was about 5×10-5Pa and the real-time pressure during the experiment was about 10-3Pa.The gas pressure at the collision point was estimated to be around a few Pa, where the contribution of N2O4could be negligible according to the calculations based on the equilibrium constant expression.[8]The rotatable hemispherical energy analyzer collected the scattered electrons at a range of scattering angles from 1.5◦to 8◦.Then the energy-analyzed electrons were counted by the position-sensitive detectors based on the microchannel plates.The real 0◦scattering angle was calibrated by checking the symmetry distribution of the inelastic scattering signals of 1s21S0→1s2p1P1transition in helium around the geometric 0◦angle.The pressure effect was safely neglected,since the absolute GOSs measured at different flow rates were found in coincidence within the experimental uncertainties at several selected angles.[30,31]

On the basis of the first Born approximation (FBA), the GOS can be derived from the experimental DCS as[23,32]

Here,f(K,En) is the momentum transfer dependent GOS,whileKandEnare the momentum transfer and excitation energy,respectively.Ψ0andΨnare theN-electron wave functions for the initial and final states.rjis the position vector of thej-th electron.p0andpaare the incident and scattered electron momenta,respectively.dσn/dΩrepresents the DCS of the corresponding transition.

To obtain the intensities for specific transitions,the measured EEL spectra were unfolded using a least-squares fitting.The absolute GOSs of the valence-shell excitations of NO2were determined by normalizing them to the GOS of the 1s21S0→1s2p1P1transition of helium,[25,33–35]which has been determined with a high accuracy both experimentally and theoretically.The experimental errors of the GOSs measured in this work mainly come from the limited angular resolution,the angle determination, the statistical counts, the normalization procedure and the least-squares fitting.The total uncertainties are estimated to be about 8%–12% and are shown in Table A1.

Within the Bethe–Born theory,[23,32,36]the OOSs can be obtained from the extrapolated GOSs at the zero limit ofK2based on the Lassettre formula[21,22]

Here,x=K2/α2is the scaled momentum transfer square with a fitted scale factorα2.The coefficientsfmare the parameters to be determined in the least-squares fitting,in whichf0is equivalent to the OOS for a dipole-allowed transition.

Based on the accurate and reliable fitted results,the Born cross sections at an incident electron energy ofE0can be determined by

whereK2minandK2maxstand for the minimum and maximum squared momentum transfers, respectively.As mentioned above, the Born ICSs show clear gap between high-energy and low-energy electron scattering.Therefore,the BE-scaling method[37,38]was proposed to obtain accurate ICSs:

whereBrepresents the binding energy.It should be mentioned that the scaling method is applicable for the dipole-allowed transitions and has been used to provide reliable ICSs for many atoms and molecules.[22,39–41]

3.Results and discussion

A typical EEL spectrum of NO2at 2.5◦is shown in Fig.1(a)and a 2D GOS density(GOSD)map vs.the energy loss and the squared momentum transfer is shown in Fig.1(b).In the least-squares fitting, the first broad band was fitted by a Pearson IV function, corresponding to the 6a1←4b2and 2b1←6a1transitions,while the transitions between 4.8 eV and 9.4 eV were simulated by several Gauss functions,and the excitation energies were fixed to the experimental data reported by Ref.[18].Here, an extra peak at 9.22 eV was introduced to reproduce the experimental data well since a shoulder can be clearly observed.The line widths for these transitions were set as free parameters in the initial fitting,and fixed at the average values of 1.5◦–3◦in the final fitting,so as to determine the transition intensities.The spectrum above 9.4 eV is characterized by the overlapping vibronic transitions of many Rydberg series, so several Gaussian peaks were used to reproduce the spectrum and the line widths were shared in each spectral fitting,and the sum GOS was given in this region.

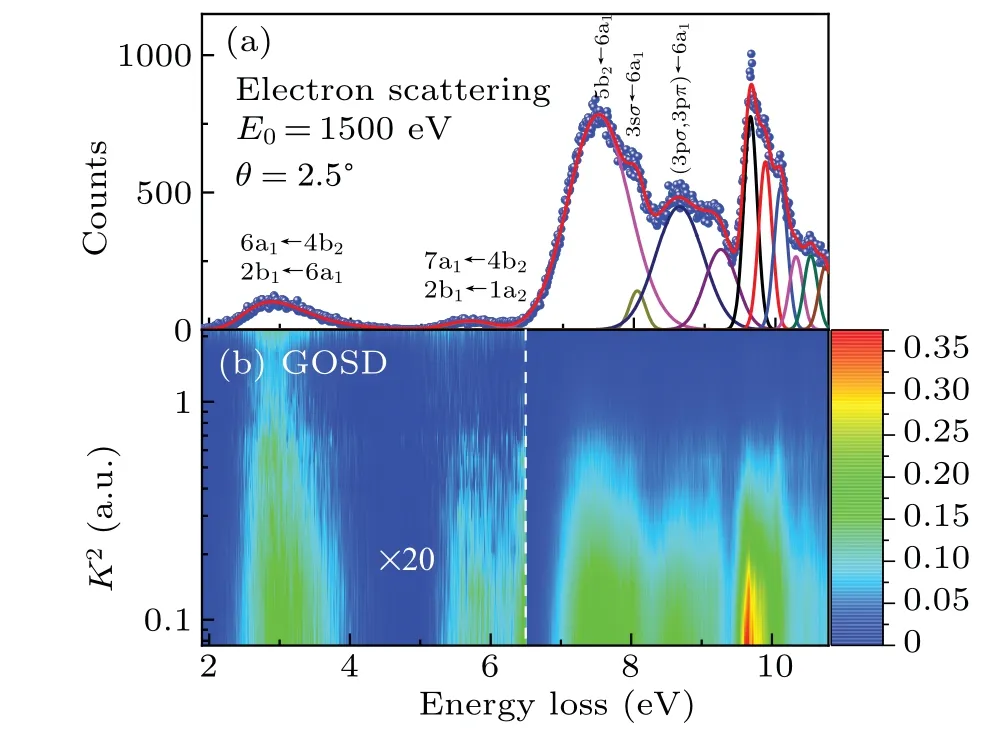
Fig.1.(a) A typical EEL spectrum of the valence-shell excitations of NO2 at an incident electron energy of 1.5 keV and a scattering angle of 2.5◦.The solid lines are the fitted curves.(b)A 2D map of the GOSDs of NO2 vs.the energy loss and squared momentum transfer.

The first broad band can be attributed to the 6a1←4b2and 2b1←6a1transitions based on the calculations of McEwen[19]and Gangi.[20]The next band can be attributed to the 7a1←4b2and 2b1←1a2transitions based on the energy-level diagram of Mulliken and Robert.[42]Note that the limited energy resolution of 70 meV is not sufficient to separate the transitions of 5b2←6a1and 3sσ←6a1, so their sum GOS is given in Fig.2(c), to avoid the error in random allocation of intensities during the fitting process.It is clear that all the GOSs in Figs.2(a)–2(d)exhibit the typical behavior of a dipole-allowed transition,i.e.,the GOS decreases with the increase ofK2and has a maximum atK2=0.The unknown nature of the unassigned salient feature at 9.22 eV shown in Fig.2(e) requires further detailed investigation,and the current GOS profile implies that the underlying transition is more likely to be dipoleallowed.The GOS of the feature at 9.38–10.38 eV is shown in Fig.2(f), which also exhibits the typical momentum transfer dependence behavior of a dipole-allowed transition.

Fig.2.Present GOSs for the excited states of(a)(6a1←4b2)+(2b1←6a1),(b) (7a1←4b2) + (2b1←1a2), (c) (5b2←6a1) + (3sσ←6a1), (d) (3pσ,3pπ)←6a1, (e) added peak (9.22 eV) and (f) 9.38–10.38 eV.The dots are the experimental data while the solid lines are their fitted curves.

Fig.3.Optical oscillator strength densities of the valence-shell excitations of NO2,along with the previous dipole(e,e)and photoabsorption results.

The OOSD of NO2at the scattering angle of 0◦was reconstructed using the extrapolated OOSs with the excitation energies and the peak profiles determined in our fitting processes,which is shown in Fig.3,along with the previous data.It is clear that the present results in the 2–4.8 eV region are in good agreement with the results of Refs.[10,12,13,17],but evidently lower than the results of Refs.[7,18] for some unknown reason.At the same time, the present cross sections in the 4.8–6.5 eV region are generally in line with the data of Refs.[9–12,15], but significantly lower than the results of Ref.[18], especially in the energy region of 5.6–6.5 eV.This phenomenon can be attributed to the effect of NO2’s dimer N2O4, since the photoabsorption cross sections of N2O4are tens or hundreds of times higher than that of NO2in this region,[11,16]resulting in that even very trace amounts of N2O4can lead to significant increase in the photoabsorption cross sections of the impure NO2.The conjecture is reasonable in view of the fact that the experiment of Auet al.[18]was done in a gas chamber,where the gas pressure at the collision point may not be low enough to ignore the effect of N2O4.For the spectrum above 6.5 eV,the present result is consistent with the results of Refs.[9,18] considering the large difference in energy resolution,indicating that the effect of N2O4may become weak in this region.

The extrapolated OOSs for the valence-shell excitations of NO2are compared with the previous experimental data quantitatively in Table 1, along with the operating pressures at which the experiments were carried out.Consistent with the OOSD results mentioned above, the present extrapolated OOS for the (6a1←4b2) + (2b1←6a1) state is in good agreement with the result of Bogumilet al.,[17]but lower than the dipole(e,e)result by about 24%[18]for unknown reason.Although the present OOS for the(7a1←4b2)+(2b1←1a2)state is slightly lower than the results in Refs.[10,11,13,15], they are still within the mutual experimental uncertainties, which demonstrates that the results obtained at low pressures are consistent with each other.Meanwhile, the data of Nakayamaet al.[9]and Schneideret al.[12]are larger than the present OOS by approximately 42%and 27%for this state, indicating that the extrapolation process to correct the contributions of N2O4based on the equilibrium constant will lead to higher values.The particularly large deviation of the OOS for this state between the dipole(e, e)measurement[18]and the other experimental results can be attributed to the effect of its dimer N2O4,as mentioned above.For the bands including (5b2←6a1) +(3sσ←6a1), (3pσ, 3pπ)←6a1, the added peak (9.22 eV) and 9.38–10.38 eV, the present extrapolated OOSs are in good agreement with the dipole(e,e)and the photoabsorption measurements within the mutual experimental uncertainties.and shown in Fig.4.Unfortunately,to the best of our knowledge,there are no other theoretical calculations or experimental measurements reported,so we strongly recommend further investigations for the ICSs of the valence-shell excitations of NO2.

Table 1.Present OOSs of the valence-shell excitations of NO2, along with the previous experimental results.The data are multiplied by a factor of 100.

Fig.4.Integral cross sections for electron impact excitations into(6a1←4b2)+ (2b1←6a1), (7a1←4b2) + (2b1←1a2), (5b2←6a1) + (3sσ←6a1), (3pσ,3pπ)←6a1,added peak(9.22 eV)and 9.38–10.38 eV.

To facilitate users, the measured GOSs and the corresponding extrapolated OOSs are tabulated in Table A1.Meanwhile, the BE-scaled ICSs are given in Table A2.All the datasets presented in this paper, including the GOSs, OOSs and ICSs,are compiled in the supplementary materials in PDF format.

Given the fact that our extrapolations are compatible with the photoabsorption and the dipole (e, e) results, the present experimental data are reliable and the fitted curves are suitable to deduce the Born or BE-scaled ICSs using Eqs.(4)and(5).Thus, the BE-scaled ICSs for the valence-shell excitations of NO2from the excitation thresholds to 5000 eV are determined

4.Summary

In this work,the low-lying electronic excitations of NO2have been studied at an incident electron energy of 1.5 keV and an energy resolution of about 70 meV.By means of the crossed-beam and relative flow techniques,absolute GOSs as a function ofK2for the excitations of(6a1←4b2)+(2b1←6a1),(7a1←4b2) + (2b1←1a2), (5b2←6a1) + (3sσ←6a1), (3pσ,3pπ)←6a1, added peak (9.22 eV) and 9.38–10.38 eV have been determined.The GOS profiles imply that the EEL spectra are dominated by dipole-allowed transitions.Thanks to the low target’s gas pressure of the cross-beam technique,the present measurement is not affected by the dimer N2O4.The origin of an unassigned state at around 9.22 eV remains unknown and requires further analyses.By extrapolating the measured GOSs with the Lassettre formula,the corresponding OOSs can be determined atK2=0 and the derived OOSs are consistent with most previous experimental results.Furthermore,the BE-scaled ICSs of the corresponding excitations of NO2have been systematically derived based on the BE-scaling method.The present oscillator strengths and ICSs can not only supplement the fundamental database for NO2but also have important applications in the fundamental research.

Appendix A:Data tables

The GOSs for the valence-shell excitations of NO2are tabulated in Table A1, along with the corresponding extrapolated OOSs,which are amplified by a factor of 103.In the first row of the table, the related scattering angles are also listed.The BE-scaled ICSs listed in Table A2 are magnified by a factor of 102.

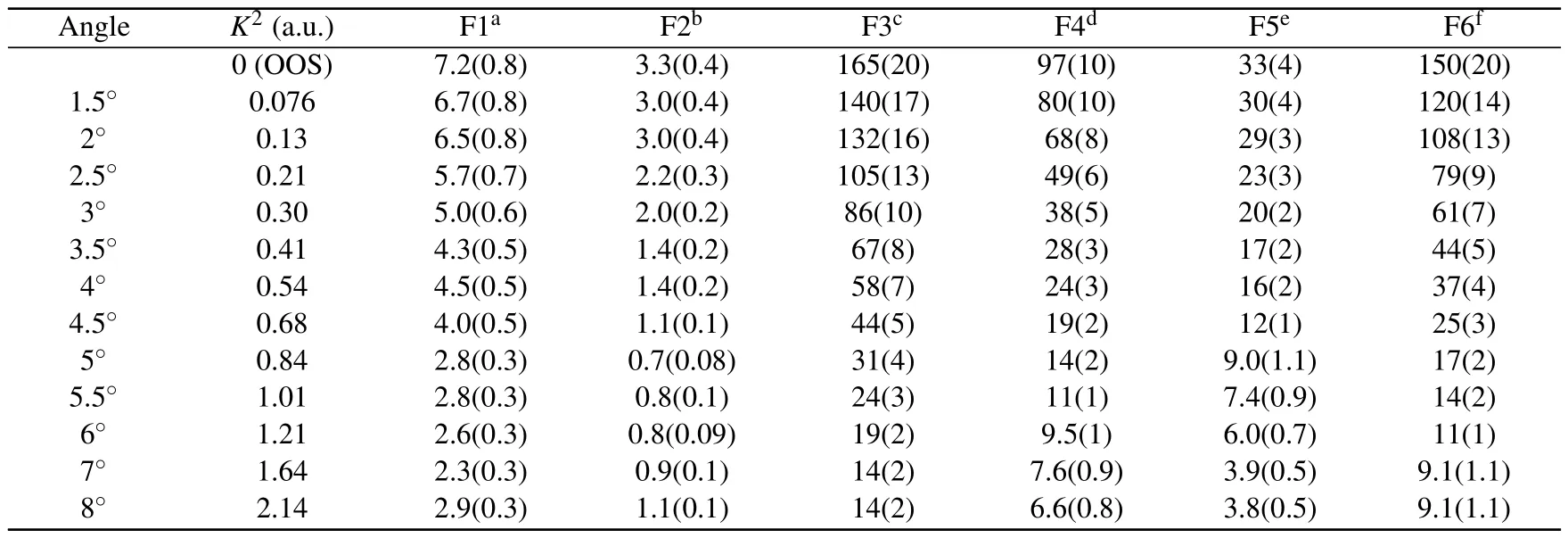
Table A1.Generalized and optical oscillator strengths of the valence-shell excitations of NO2.

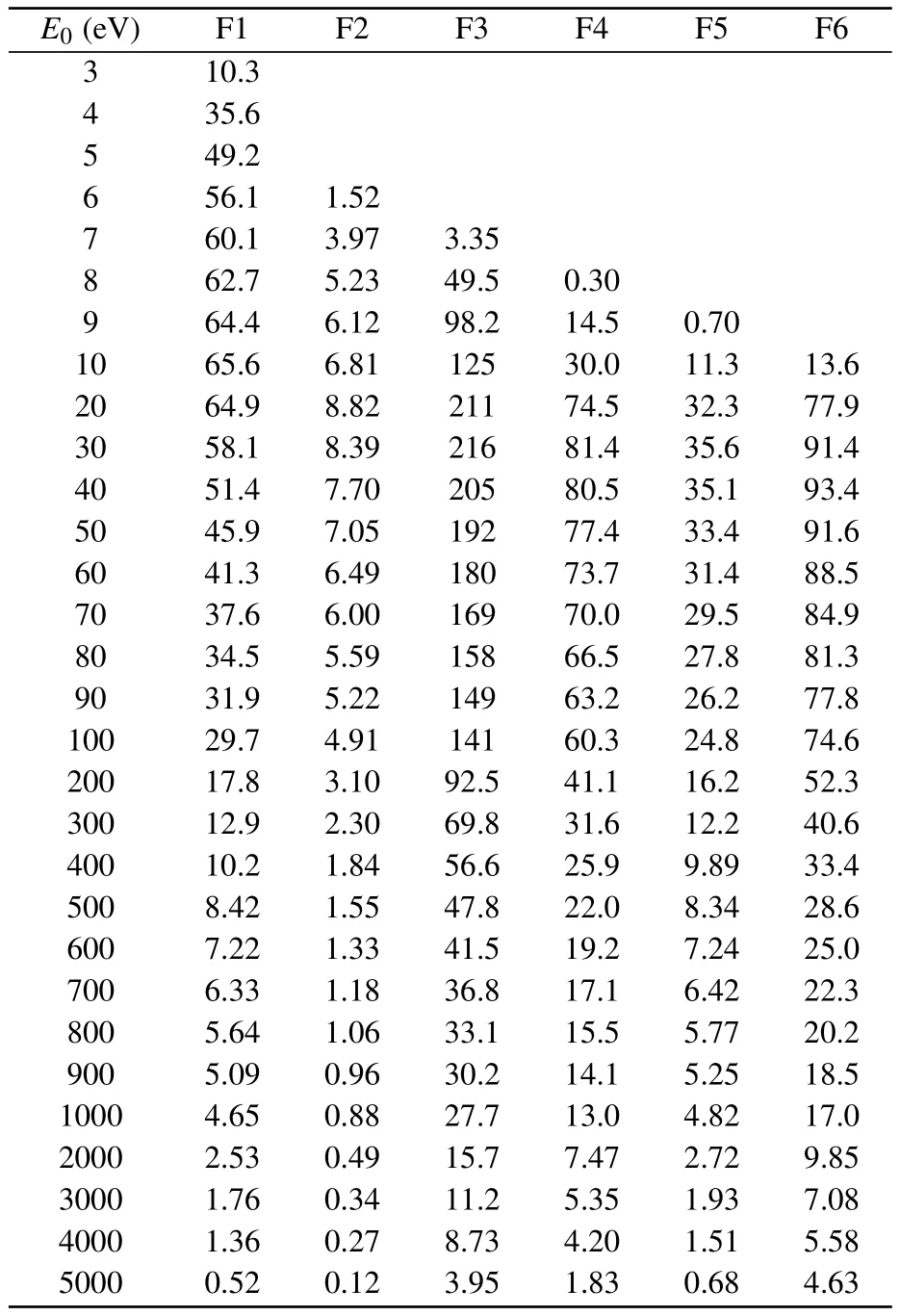
Table A2.BE-scaled ICSs for the electron impact excitations to the features F1–F6,which have been identified detailedly in Table A1.The unit of the ICSs is a.u.

Data availability statement

The data that support the findings of this study are openly available in Science Data Bank at https://doi.org/10.57760/sciencedb.j00113.00156.

Acknowledgements

Project supported by the National Key Research and Development Program of China (Grant No.2022YFA1602500)and the National Natural Science Foundation of China(Grant Nos.12334010 and U1932207).