Blind quantum computation with a client performing different single-qubit gates

Guang-Yang Wu(吴光阳), Zhen Yang(杨振), Yu-Zhan Yan(严玉瞻),Yuan-Mao Luo(罗元茂), Ming-Qiang Bai(柏明强),†, and Zhi-Wen Mo(莫智文)

1School of Mathematical Sciences,Sichuan Normal University,Chengdu 610068,China

2Research Center of Sichuan Normal University National-Local Joint Engineering Laboratory of System Credibility Automatic Verification,Chengdu 610066,China

3Institute of Intelligent Information and Quantum Information,Sichuan Normal University,Chengdu 610068,China

Keywords: blind quantum computation,verifiable blind quantum computation,single server

1.Introduction

As is well known, quantum computation has significant advantages over classical computation in solving some problems.[1,2]This means that quantum computation may become essential for many people in the future.However,Feynman[3]pointed out that it is impossible to represent the results of quantum mechanics with a classical universal device,this may prompt some people to explore how to build quantum computers.Actually, when the first generation of quantum computers comes out, they may be accessible to a few people around the world.In other words,many people cannot access to use quantum computers directly.Thus,when someone wants to use a quantum computer to achieve computation,he may delegate his quantum computation to the owner of the quantum computer.Unfortunately, some private information may be leaked out in this process.To solve this problem,researchers proposed the idea of blind quantum computation(BQC).

Childs[4]firstly proposed the BQC protocol in 2005.In that protocol,the client needs to prepare quantum states,store quantum states, and perform the SWAP gate.Since then,many BQC protocols have been proposed one by one.[5–13]For example, Broadbentet al.[12]proposed the first universal blind quantum computation(UBQC)protocol.Compared with Ref.[4], that protocol further limits the quantum ability of the client.In the protocol, the client only needs to prepare single-qubit states.Based on the fact that measuring single-qubit states is easier than preparing single-qubit states in experimental setups,Morimae and Fujii[13]proposed a new type of BQC protocol in 2013,where the client needs to measure single-qubit states rather than to prepare single-qubit states.Moreover,some BQC protocols have been experimentally demonstrated.[14,15]

To make the client completely classical in the BQC protocol,some scholars have made in-depth research.For example,Broadbentet al.extended the UBQC protocol to a doubleserver protocol in Ref.[12],in which the client is completely classical.After this,Liet al.[16]proposed a triple-server BQC protocol.Then,Xuet al.[17]modified this protocol to a singleserver BQC protocol.They both declared that the client is completely classical in their respective protocols.However,Hung and Hwang[18]pointed out a security loophole in those two protocols.Even more unfortunately, Morimaeet al.[19]declared that the client cannot be completely classical in the single-server BQC protocol.Thus, making the client as classical as possible becomes a hot research in single-server BQC protocol.

It is worth noting that verifiability is an important property in the BQC protocol.This means that the client can make sure the result of delegate quantum computation to be correct or incorrect.In order to achieve this goal,some verifiable BQC protocols are proposed.In 2015, Hayashi and Morimae[20]proposed a protocol based on the fact that graph states can be completely specified by a set of stabilizer operators.In 2017,Fitzsimons and Kashefi[21] proposed the unconditional verifiable blind quantum computation (VUBQC) protocol according to the way of the UBQC protocol.In those two protocols,the client can verify the correctness of the delegated quantum computation according to whether the server is honest or dishonest.

In 2021,Liet al.[22]proposed a new type of BQC protocol,where the client only needs to perform a few single-qubit gates.Specifically,the client needs to perform the gatesH,Tor the gatesT,X.As we all know,the gatesH,Tcan be used to fit any single-qubit gates.In order to further limit the quantum ability of the client, we propose two single-server BQC protocols in this paper.The first protocol allows the client to perform the gateT.In the second protocol, the client is allowed to perform the gatesT,X.In addition, the client does not have any quantum abilities in these two protocols.Although we weaken the quantum ability of the client, our protocol can still achieve verifiable blind quantum computation.

The rest of this paper is organized as follows.In order to better understand the proposed protocols,we first review a related protocol in Section 2.Section 3 will be divided into two subsections to propose our two protocols.Section 4 analyzes the proposed protocols from two aspects,i.e.,correctness and safety.Finally,we provide conclusions in Section 5.

2.Preliminaries

(A3)Alice sends all single-qubit states to Bob.Then Bob performs the gateCZto entangle them according to the graph stateG, where an embedding ofTtrap qubits andDdummy qubits can be admited.

(A4)Alice asks Bob to measure the following qubits: (1)If the qubit is a computation qubit, it will be measured in the basis{|±δ〉}, whereδ=φ′+θ+rπ,θis the angle of the qubit in(A2),φ′is a modification ofφaccording to previous measurement results,φis the actual measurement angel,ris encryption to the result.(2) If the qubit is a trap qubit, Bob can use the basis{|±(θ+rπ)〉}to measure it.Similarly,θis the angle of the qubit in(A2),ris encryption to the result.(3) If the qubit is a dummy qubit, it will be measured in the basis{±θ},.After Bob measures the qubit,he sends the measurement result to Alice.

(A5)After all qubits were measured,Alice will check the results of trap qubits.If all results of trap qubits are correct,then Alice can think that Bob does not perform any malicious operations.Finally, Alice undoes the impact ofrto recover the correct outcome of this delegated quantum computation;otherwise the protocol will be stopped.

3.Main protocol

3.1.Blind quantum computation with a client only performing the gate T

In this subsection,the client Alice only performs the gateT.Suppose that Alice wants to achieve the same goal like the VUBQC protocol.Now,she wants to finish her computation on theN-qubit graph state corresponding to the graphG,whereN=M+T+D.The graphGadmits an embedding ofDdummy qubits andTtrap qubits.The process of this protocol is shown in Fig.1.

Fig.1.Blind quantum computation with a client only performing the gate T.

The specific steps are given as follows:

(T1) Alice asks Bob to prepareM+T+D+Squbits in state|+〉.These qubits will be divided into three sets,the setP1is made up ofM+Tqubits,in whichMqubits for computation andTqubits as trap qubits;Dqubits as dummy qubits make up the setP2; the rest ofSqubits as decoy qubits make up the setP3.

(T3) Alice asks Bob to perform the gateHonce on all qubits.

(T4)Bob sends a qubit to Alice,then Alice performs one of the following operations: (i)If the qubit is from the setP1,Alice will do nothing.(ii)If the qubit is from the setP2,Alice will perform the gateTon it for 2 times or 6 times in order to make the state of the qubit be|+〉or|-〉.(iii)If the qubit is from the setP3, Alice will perform the gateTon it for 2 times in order to make the state of the qubit be one of the set{|0〉,|1〉,|+〉,|-〉}.Finally,Alice returns the qubit to Bob.

(T5)Alice reveals which qubits belong to the setP3,then she asks Bob to measure theseSdecoy qubits in the basis{|+〉,|-〉}or{|0〉,|1〉}.After Bob measured these decoy qubits, Alice and Bob will compare the results.If Bob can always publish the correct result when he chooses the right basis, Alice and Bob can make sure that there is no attack;otherwise the protocol aborts.

(T6) Alice asks Bob to perform the gateHonce on all qubits again.

(T7) Alice and Bob use these qubits to perform the VUBQC protocol.

3.2.Blind quantum computation with a client performing the gates T,X

In this subsection,the client Alice can perform the gatesT,X.Actually, based on the fact thatHXH=Z, the client can also perform the gateZ.Now,suppose that Alice wants to achieve the same goal like the VUBQC protocol and finish her computation on theN-qubit graph state corresponding to the graphG.Figure 2 shows the process of the protocol,in which the values ofi,j,kwill be 0 or 1.

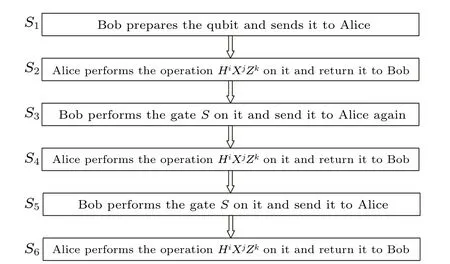
Fig.2.Blind quantum computation with a client performing the gates T,X.

The specific steps are given as follows:

(S1) Alice asks Bob to prepareM+T+D+Squbits in state|0〉,whereM=M1+M2+M3,T=T1+T2+T3.These qubits will be divided into five sets, the setWiis made up ofMi+Tiqubits, in whichMiqubits for computation andTiqubits as trap qubits,i=1,2,3;Dqubits as dummy qubits make up the setW4;the rest ofSqubits as decoy qubits make up the setW5.

(S2)Bob sends a qubit to Alice,then Alice performs one of the following operations: (i) If the qubit is from the setW1, Alice will perform the corresponding single-qubit gate to make the state of the qubit be|+〉 or|-〉, where|+〉 =H|0〉=XH|0〉,|-〉=HX|0〉=HXHXH|0〉.(ii)If the qubit is from the setW5,Alice will perform the corresponding singlequbit gate to make the state of the qubit be|0〉 or|1〉, where|0〉=|0〉=HXH|0〉,|1〉=X|0〉=XHXH|0〉.(iii)If the qubit is from other sets,Alice will do nothing.Finally,Alice returns the qubit to Bob.

(S3) Alice asks Bob to perform the gateTonce on all qubits.

(S5) Alice asks Bob to perform the gateSonce on all qubits.

(S6)Bob sends a qubit to Alice,then Alice performs one of the following operation: (i) If the qubit is from the setW1orW2, Alice will do nothing.(ii) If the qubit is from the setW3,Alice will perform the corresponding single-qubit gate to make the state of the qubit be|+〉 or|-〉.(iii) If the qubit is from the setW4,Alice will perform the corresponding singlequbit gate to make the state of the qubit be|0〉 or|1〉.(iv) If the qubit is from the setW5,Alice will perform the corresponding single-qubit gate to make the state of the qubit be one of{|0〉,|1〉,|+〉,|-〉}.Finally,Alice returns the qubit to Bob.

(S7)Alice reveals which qubits belong to the setW5,then Bob measures theseSdecoy qubits on the bases{|0〉,|1〉}or{|+〉,|-〉}.After Bob measured these decoy qubits,Alice and Bob will compare the results.If Bob can always publish the correct result when he chooses the right basis,Alice and Bob can make sure that there is no attack; otherwise the protocol aborts.

(S8) Alice and Bob use these qubits to perform the VUBQC protocol.

4.Analysis

Obviously,if there is an outside attacker in these two protocols, she or he will be discovered with a high probability when Alice asks Bob to measure the decoy qubits.Thus, the outside attacker will be ignored when complaining the correctness of these two protocols.

Theorem 1Assume that Bob follows the step of these two protocols,then the outcome is correct.

Theorem 2In these two protocols,Bob cannot learn any useful information about the actual input, output and algorithm.

ProofIn the first protocol, the state of the qubit will beHT jHTi|+〉 when Alice and Bob perform the corresponding operations.In the whole process, Bob does not know how many times Alice performed the gateTon the qubit.Based on this fact, Bob does not know the actual values ofiandj.This is the reason why he cannot get any information about the actual state of the qubit.Thus,Bob cannot learn any useful information about the actual input, output and algorithm when they use these qubits to perform the VUBQC protocol.

In the second protocol, Alice will perform three quantum operations in the whole process.These operations will be recordedU1,U2,andU3.Firstly,when Alice performs the operationU1on the qubits, the states of the qubits belong to the set{|0〉,|1〉,|+〉,|-〉}.Secondly,when Alice performs the

5.Conclusions

In the single-server BQC protocol, there are main three models according to the quantum ability of the client.The first model is proposed by Broadbentet al.,[12]it allows the client to prepare the single-qubit states.Morimae and Fujii[13]proposed the second model,where the client needs to measure the single-qubit states.The third model is proposed by Liet al.,[22]it allows the client to perform the single-qubit gates.Obviously, the first two protocols proposed are based on the third model.Compared to Ref.[22], the proposed protocols further limit the quantum ability of the client.Specifically,the first protocol allows the client to perform the gateTrather than the gatesH,T; the second protocol allows the client to perform the gatesT,Xinstead of the gatesH,T.

The proposed protocols require bidirectional transmission of quantum states between client and server.As we all know,quantum states will encounter some unavoidable problems in the process of transmission.For example,they will be affected by noise when they are transmitted in the channel.Compared with one-way transmission of quantum states, bidirectional transmission of quantum states is more affected by noise.Up to date, there are some BOC protocols[23–26]that can resist the effects of noise.These protocols mainly use entanglement distillation and error-correcting codes to resist noise, both of which require some quantum power.If these two methods are simply added to the proposed protocol,it may be contrary to the original intention of the proposed protocol.When the client only can perform a few single-qubit gates, what methods should be taken to resist the noise? This is a question worth thinking about.

Acknowledgments

Project supported by the National Science Foundation of Sichuan Province (Grant No.2022NSFSC0534), the Central Guidance on Local Science and Technology Development Fund of Sichuan Province (Grant No.22ZYZYTS0064), the Chengdu Key Research and Development Support Program(Grant No.2021-YF09-0016-GX), and the Key Project of Sichuan Normal University(Grant No.XKZX-02).