Rectified transport of a single vibration-driven vehicle in the asymmetric channel

Yu-Wen Hao(郝钰文), Bao-Quan Ai(艾保全), Fei Tan(谭飞), Xiao-Yuan Yu(余孝源), and Feng-Guo Li(李丰果)

Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510631,China

Keywords: self-propelled particle,rectification,vibration-driven vehicle

1.Introduction

Active matter is a rapidly growing branch of nonequilibrium soft matter physics with relevance to chemistry, biology, and complex systems.[1–3]Self-propelled particles are assumed to have an internal propulsion mechanism,which can use energy from an external source and transform it under nonequilibrium conditions into directed motion.Compared to passive particles,active particles moving in confined structures could exhibit peculiar behaviors, resulting, for example,in collective motion in complex systems,[4–6]spontaneous rectified transport,[7–11]separation of active particles based on their swimming properties,[12–16]phase separation of selfpropelled particles,[17–20]trapping particles in microwaves,[21]spiral vortex formation in circular confinement,[22]depletion of elongated particles from low-shear regions,[23]and other interesting transport phenomena.[24–26]

In recent years, the ratchet transport of self-particles has also attracted much attention.Ratchets are examples of simple nonequilibrium model systems which can rectify zero mean nonequilibrium fluctuation into unidirectional motion.[27,28]The rectification phenomena of self-propelled particles were first observed in the presence of asymmetric rigid boundaries,like the sawtooth profile of microfabricated cogs or an array of funnel-shaped apertures.Experimental studies[9,29–32]have shown the key role of self-propulsion for driving a nano-sized ratchet-shaped wheel(active particles are able to drive asymmetric ratchets,rotors,and gears),or for rectifying the cell motion in an array of asymmetric funnels(the external vibration excites macroscopic particles).Theoretical studies[13,33–36]have found that the rectification phenomenon of overdamped swimming bacteria occurs in a system with an array of asymmetric barriers.In a general asymmetric channel with upside–down or right–left asymmetry,chiral microswimmers can generate a direct particle flow.These studies mainly utilize the asymmetry of the restricted structures or barriers to rectifying particle transport.[35]Wuet al.found that channel boundaries also play an important role in the motion of active particles.[37]The rectification effects in the channel with soft walls are better than those in the channel with hard walls.Huanget al.numerically studied the effect of changes in the channel’s upper wall on transport and found that different channel shapes lead to different rectification effects.[27]

Previous studies have often focused on the collective behavior of active particles and rarely investigated the effect of channel boundaries experimentally.In this paper, we build a two-dimensional asymmetric double-opening channel and use an experimental approach to investigate the rectification effect of channel width and inter-channel asymmetry variation on individual particles.Gravity is also introduced to see whether the addition of external forces can counteract the effect of the structure.

2.Experimental setup and method

The schematic diagram in Fig.1(a)shows the experimental setup.We used a ratchet device proposed by Prof.Ai Baoquan as the confining structure, which consists of a pair of asymmetrical wedge-shaped baffles placed opposite each other,[38,39]whereLis the length of the outer rectangle of this restraint structure,2H+Dis the width of the outer rectangle,andDis the width of the channel.The channel shape is described by the halfwidthh(x)as follows:

The parameter∆is used to describe the degree of asymmetry between the left and right channels in the structure,where∆=|L1-L2|/L.In the long asymptotic region,the mean particle velocity along thex-direction is

whereNis the total number of experiments.We use the velocity to define the rectification efficiency of the particle

whereV0is the initial velocity of the particle.In this paper,we first build the device using the case when∆=0.4.Before the experiment began, a laser infrared level collimator(Syntek standard model) with an accuracy of 0.01◦was first used to measure the table level,and the unevenness of the table was measured to 0.00◦, which excluded the influence of system error.Next,a plexiglass(PMMA)board with a thickness of 10 mm and a size of 400×250 mm was placed on the experimental platform, and then four pieces of the same kind of plexiglass with a thickness of 5 mm and different lengths(two pieces each ofS1=300 mm andS2=600 mm) were assembled on it to form a symmetrically curved rhombus-like structure and fixed.

Our self-propelled particle is a vibration-driven vehicle (VDV), commercially available Hexbug Nano(Fig.1(a)).[40–43]The length, width and height of the vehicle is 43 mm, 15 mm and 18 mm respectively.It is powered by a built-in 1.5 V button battery and covered with a layer of elastic resin.The only limiting factor for the VDV in motion is battery life.When the battery power is reduced,the movement of the agent slows down significantly.In order to prevent the effect of battery power,we replaced the battery every hour(manufacturer: HEXBUG,battery life: 4 h).

Fig.1.Schematic diagram of the experimental setup.(a)A ratchet device was placed on the mounted platform with a camera mounted on it to record VDV movement.(b) The structure of the ratchet device: the VDV is released from the external rectangular center of gravity A at different initial angles, where D is the width of the opening and ϕ is the bending angle of the baffle.The length of the outer rectangle L is 79 cm, and the lengths of the two sections L1 and L2 are 22.5 cm and 56.5 cm, respectively.The lengths of the baffles on both sides S1 and S2 are 30 cm and 60 cm,respectively.(c)Actual VDV diagram.(d)The case where the bottom plate on the left side of the device is padded,where α is the base plate elevation angle and M is the base plate length. M=100 cm.

We took the center of gravity A of the outer rectangle of the rhombus-like structure as the initial position of the VDV motion.Then we used a marker to mark the angle clockwise at 5◦intervals with A as the center until 360◦(coinciding with 0◦).The 0◦position was indicated by the negative direction of thex-axis.The following steps were followed for each of the next experiments: Hold the VDV with a pair of tweezers and aim the direction after placing its center at point A.Release it while the stopwatch starts timing and observe its movement in the arena.Remove the VDV as it moves to the exit and stop the stopwatch.Record its exit and moving time.A video camera (GoPro Hero-5) was kept directly above the platform to record the motion.The videos were recorded at a rate of 60 fps.The trajectory was plotted by SO-Tracker software(a program based on the neural network SiamMask).

We investigated separately the effect of three factors —the range of channel widths,inter-channel asymmetry,and the addition of gravity—on the correction of the motion of a single self-propelled particle in the channel.The first two were achieved by widening the baffles on both sides and changing the baffles’angle.To study the effect of gravity,we prepared 30 0.9 mm thick one-yuan coins currently on the market and divided them equally into three groups.The three groups of coins were padded at the center of the left edge of the bottom plate and both ends, so that a certain inclination angleαwas formed between the bottom plate and the horizontal table surface.Differentαwould cause the VDV to obtain different gravitational forces, so each change inαwould decrease evenly by one coin.For each change in each of these three variables,we changed the initial motion angle of the VDV 721 times (ranging from 0◦to 360◦at 0.5◦intervals) to ensure a sufficient amount of data.

3.Results and discussion

When there is no perturbation and the channel width is large enough, a chiral self-propelled particle will repeat the circular motion.[43,44]The motion is described by the orientationθ(t)

whereωcis an angular frequency that relates to the natural curvature of the trajectory andωcη(t)is a Brownian orientational noise in angular frequency units(rad·s-1).The particle trajectory is obtained from the orientation of the velocity

wherevis the velocity of the particle.The ratiov/ωcis the radius of the circular trajectory in the limitη(t)=0.For a numerical solution of Eqs.(4)–(6),a discrete formulation is used with

whereE∆tis a dimensionless noise for a time step resolution∆t.It verifies〈E∆t〉=0 and〈E∆t2〉=Drot(1/ωc∆t)withDrotan orientational diffusion coefficient.

Due to the limitation of the channel width,the chiral particle will collide with the channel walls in a completely elastic manner.As the particle moves to the sides of the channel, the channel width shrinks continuously.More and more frequent collisions will continuously correct the direction of particle motion toward the exit,and thus directional transport occurs.

Figure 2 shows the dependence of rectification efficiency on the range of channel widths.Figures 2(a) and 2(b) depict the transport of the self-driven particle within the left and right channels,respectively,as the channel widthDincreases,

whereϕ=105◦and the degree of asymmetry∆between the two channels is 0.4.There are differences in the shape of the left and right channels, with the left channel being wide and short and the right channel being narrow and long.We use box plots to represent the statistical results of the particle rectification efficiencyη.The upper and lower ends of the boxes correspond to the upper and lower quartiles of the data set,respectively,with a factor of 1.5 for data outliers.The distribution ofηdoes not change linearly with increasingDbut fluctuates.As shown in Fig.2(a),the distribution ofηis more concentrated at 50 mm and 80 mm,but in a relatively low range.There exists the most unfavorable value ofD.The mean and median values ofηatD=80 mm are lower and the values are more unevenly distributed.It explains that particles will have a lower probability of leaving the channel quickly if released in this case.Similar results can be observed in Fig.2(b),except that the most unfavorable value ofDbecomes 20 mm.This means that this value is not fixed and has different expressions for different channel shapes.

Figure 3 depicts the dependence of the rectification efficiency on the degree of channel asymmetry.The shapes of the two channels are identical for an asymmetry degree∆of 0.∆=0.4 forϕ=105◦and∆=0.3 forϕ=120◦.From Figs.3(a) and 3(c), the boxes atϕ=120◦are found to be significantly shorter and lower, regardless of channel width.Correspondingly,the median and mean values atϕ=120◦are below those at 105◦, except for a higher median at the left channel width of 20–35 mm(see Figs.3(b)and 3(d)).The decrease in asymmetry greatly compresses and reduces the range ofηvalues,but does not significantly affect the uniformity of theηdistribution.It indicates that the decrease in asymmetry—the proximity of the shape between the two channels—is not conducive to the correct transport of the particle.

Fig.3.(a)and(c)Box plots of particle rectification efficiency η at different channel widths for asymmetries between channels ∆=0.3 and∆=0.4.(b)and(d)The corresponding median line plots.

Figure 4 explores whether the addition of gravity can affect rectification transport.With the left bottom plate raised,gravity provides a force component on the particle down the slope.As expected, the likelihood of the particle exiting the right channel continues to increase as the angle increases.Atα=3.45◦, gravity cancels out the effect of the structure,bringing the probability of the particle leaving through the two channels to unity(shown in Fig.4(a)).

However, from Fig.4(b), we find an interesting phenomenon—the rectification efficiencyηof the particle does not change with the angle.For the left channel, the data distribution is unchanged except at 0.52◦,except for some fluctuations in the median and mean values.For the right channel,the distribution of the data appears to be related only to the presence or absence of the angle,not to the size of the angle.

To further investigate this phenomenon,we used the SOTracker software to track the moving particle and obtain an image of its trajectory.We chose images with an initial angle of 150◦—the particle released from this direction is usually able to move in the channel for a longer period of time.

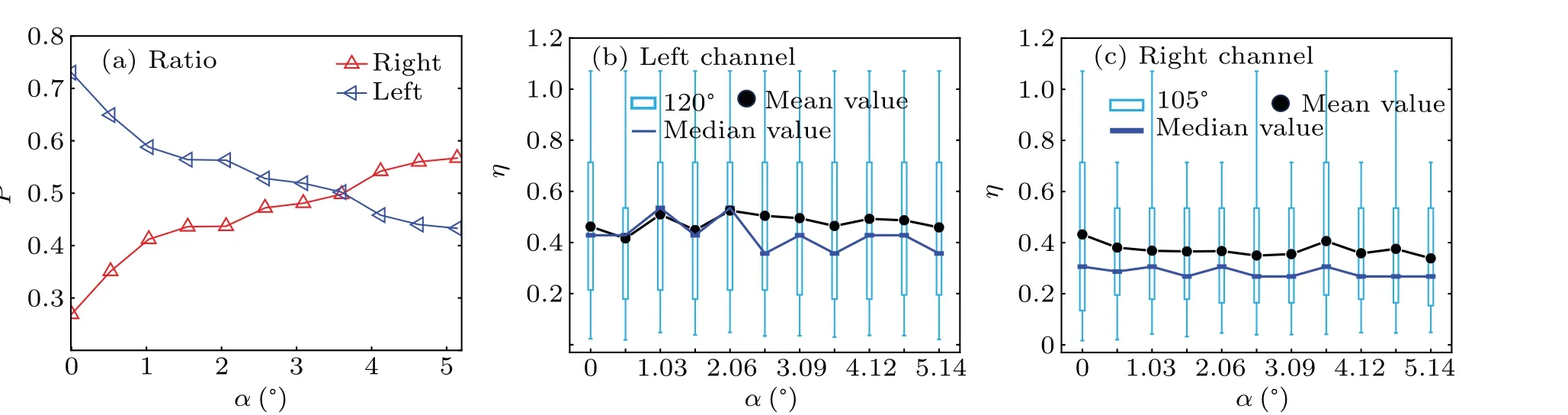
Fig.4.(a) The ratio of the particle leaving from the two channels under different tilt angles.(b) and (c) Box plots of particle rectification efficiency η for different tilt angles α when the degree of asymmetry between channels ∆=0.3 and the channel width D=50 mm.

As shown in Fig.5(a),the particle makes a counterclockwise circular chiral motion within the channel.Collisions change the direction of movement of the particle and cause it to leave.When not affected by gravity,the motion trajectory is uniformly distributed.Once the angle begins to appear,the particle is bound to convert some of its kinetic energy into its gravitational potential energy.This will weaken the particle’s ability to move and prevent it from colliding with the wall at the right location,which in turn increases the number of turns it makes and ultimately leads to a decrease in rectification efficiency(see Figs.5(b)–5(d)).

Fig.5.The trajectory of the particle at different tilt angles.

Due to the asymmetry of the two sides of the channel,the right channel is narrower and longer than the left, so the particle must pass through collisions if it wants to leave.The left channel,on the other hand,is wider and the particle can leave without collision from some specific initial angle.As a result,the range of rectification efficiency dataηin the left channel does not fluctuate much, while the overall right channel decreases.

4.Conclusion

In this work, we experimentally investigated the rectification transport behavior of a single self-driven particle in a two-dimensional asymmetric double-opening ratchet channel.The rectification efficiency of the single particle moving from the center of the structure to the exit was analyzed under three factors—the range of channel widths, the degree of channel asymmetry,and the tilt angle of the platform.It was found that the structure has a major effect on transport.Transport efficiency does not change linearly with increasing channel width and the most unfavorable width value exists.This value is not fixed and has different expressions for different channel shapes.The weakening of the asymmetry between the two channels significantly reduces the efficiency of particle transport in them.The addition of external gravity does not counteract the structural constraints on transport,but only affects the probability of the particle leaving through the exit.This study investigates the phenomenon of particle rectification from an experimental point of view, and provides a technical and experimental reference for future studies on the rectification of multiple particles.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant No.12075090).