Spontaneous isospin polarization and quantum Hall ferromagnetism in a rhombohedral trilayer graphene superlattice

Xiangyan Han(韩香岩), Qianling Liu(刘倩伶), Ruirui Niu(牛锐锐), Zhuangzhuang Qu(曲壮壮),Zhiyu Wang(王知雨), Zhuoxian Li(李卓贤), Chunrui Han(韩春蕊), Kenji Watanabe,Takashi Taniguchi, Zizhao Gan(甘子钊), and Jianming Lu(路建明),‡

1State Key Laboratory for Mesoscopic Physics,School of Physics,Peking University,Beijing 100871,China

2Institute of Microelectronics,Chinese Academy of Sciences,Beijing 100029,China

3University of Chinese Academy of Sciences,Beijing 100049,China

4National Institute for Materials Science,1-1 Namiki,Tsukuba,305-0044,Japan

Keywords: rhombohedral trilayer graphene, moir´e superlattice, symmetry breaking, flavor polarization, van Hove singularity,quantum Hall ferromagnetism

1.Introduction

Exotic quantum phases including superconductivity, ferromagnetism, and Chern insulators emerge at the moir´e interface that hosts strongly correlated electrons.[1–13]The key may lie in the fact that electronic correlation results in flavor symmetry breaking between spin and valley degrees of freedom,[14–20]owing to fulfillment of the Stoner criteriaρU>1,whereρis density of states(DOS)on the Fermi surface andUis the on-site energy.With the lifted degeneracy,for example,electrons residing at only one ofKand-Kvalleys,orbital magnetic moment with broken time reversal symmetry would arise, leading to ferromagnetism and a nonzero Chern number.[21]While the origin of superconductivity so far has been highly debated,[1,2,22–25]the universal observation of superconductivity close to transition boundaries of nondegenerate phases implies its inherent connection to isospin fluctuation,[26]mimicking the antiferromagnetic spin fluctuation in cuprate.As a result, it is of high interest to investigate how the symmetry is broken at fractional commensurate fillings of the flat moir´e band.In twisted bilayer graphene,both transport and thermodynamic measurement[14,17,19,20,27]reveal that carriers tend to reset at integer multiple of full filling of one flavor,i.e.,carriers of all partially filled flavors turn into a specific flavor to make the latter fully filled; Since the full flavor cannot contribute to electric conduction, the mobile carrier density is reset to zero.During the whole process,the carrier type, nevertheless, is unchanged.By contrast, in twisted mono-bilayer graphene,[28–31]there are different types of carriers(electrons and holes)on the two sides of the phase boundary,which infers that a new band edge(stemming from the phase transition and the associated energy gap)emerge before the commensurate filling.Such detailed difference may reflect the delicate energy competition between various ground states in different moir´e systems, which in turn controls the aforementioned exotic phenomena.

In this work,by studying zero-degree twisted rhombohedral trilayer graphene (ABC-TLG) and hexagonal boron nitride, we find distinct symmetry-breaking transitions coexisting in the same sample but depending on the direction of displacement fields.At fractional fillings of the moir´e band, a correlation gap can be observed before the flavors are fully filled at a positiveD, but at a negativeDit does not emerge until the commensurate filling is achieved.In addition,in the proximity of zeroDflavor symmetry breaking is found to be invoked by a strong magnetic field,owing to the narrow bandwidth of Landau levels.The quantum Hall ferromagnetism,as expected,lifts spin,valley,and even orbital degeneracies.Our work demonstrates a rhombohedral trilayer graphene superlattice as a good platform to investigate correlation-induced symmetry breaking at phase boundaries, paving the way to tune quantum phases in strongly correlated systems.

2.Results

Pristine trilayer graphene flakes are micromechanically exfoliated onto silicon wafers from natural graphite.The rare rhombohedral part is distinguished from Bernal trilayer graphene by Raman spectrum of two-dimensional(2D)peaks at 2700 cm-1.[32,33]Then it is encapsulated by hexagonal boron nitride (hBN) flakes with the top hBN crystallographically aligned,and a moir´e superlattice is formed as a result of the small lattice mismatch between graphene and hBN crystals (see schematics in the inset of Fig.1(a), where the superlattice unit cell and lattice constantλare depicted).The measurement scheme is illustrated in Fig.1(a),where the top gateVtand the bottom gateVbare used to tune the carrier densitynand displacement fieldDindependently.The definition is as follows:n=Db+Dt,D= (Db-Dt)/2, withDb(t)=ε0εrVb(t)/db(t),εris the relative dielectric constant of hBN,db(t)is the thickness of the bottom(top)hBN flake.For convenience,we further definevs=4n/ns,wherensis the carrier density accommodated by the moir´e band.

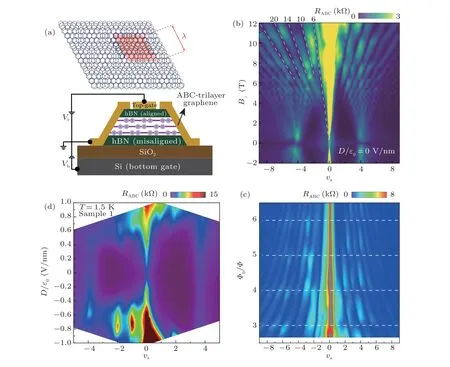
To determine the twist angle between graphene and the top hBN flake, Hall carrier density is measured to obtain the gate capacitance and thus electron concentration of full filling of moir´e bandsnscan be obtained.Asnsis directly related withλ(the inset of Fig.1(a)),we finally obtain the superlattice constant and twisted angle.A more precise method is shown in Figs.1(b) and 1(c), in which Landau fan atD=0 V/nm shows significant Brown–Zak oscillation[34–36]and we can fit the superlattice constant as 12.4 nm.Using formula[37]

wherea=2.464 ˚A is the graphene lattice constant,δ=0.018 is the lattice difference between hBN and graphene, we get the twist angleθas 0.2◦.The result agrees with the Hall effect shown in Fig.2, where at full filling of the moir´e bandnH=3×1012cm-2is obtained and the derivedλfrom the formula 1/n=is 12.41 nm.With these parameters,one can plot the phase diagram as a function ofDandvsin Fig.1(d).Atvs=0(charge neutral point,CNP),resistance increase fast with increasing|D|.TheD-sensitive bandgap opening is consistent with the rhombohedral stacking order of a trilayer graphene.[38,39]Atvs=±4,resistance peaks indicate the superlattice gap is generated,but is smaller than that of CNP in magnitude.In between, correlated insulators atvs=-1,-2 can be observed at both positive and negative displacement fields,[10–13]but their specific ranges ofDare different.The strongDdependence suggests that intrinsic properties are also effectively tuned byDfields,such as van Hove singularity(the origin of electronic correlation)and flavor polarization.

3.Distinct flavor polarization at positive and negative D

In Fig.2(a), we map the filling factor derived from antisymmetrized Hall signalvH=4nH/ns,wherenH=-1/(eRH).The definition of VHS isRH=0, which means the nominal densityvHat VHS is divergent.[31]In other words,vHin adjacent to VHS is either positive or negative infinity, which can be identified by transition from deep blue to deep red as shown in the inset of Fig.2(b).In addition,there are two other types:one is bandgap, the other is carrier reset.The former stands for carriers evolving gradually from electron to hole with zero net carriers in the middle,so that the color changes from light blue to light red.The latter is similar, but without changing carrier type:vHfirstly decreases to zero (or a finite value in practical experiment) then rises again.Consequently, during the transition the color changes into white then blue/red again.Based on these categorizations,[2]we get a schematic diagram in Fig.2(b).

Similar to many multilayer graphene like twisted mono-bilayer graphene[28–31]and twisted double bilayer graphene,[40–42]the VHS has a close relationship withD.An interesting feature of VHS is the significant jump: in the low-Dregime VHS is located very close to the full filling point of the moir´e band (FFP), however, it jumps to the vicinity of CNP at relatively largeDwhere correlated insulators emerge.As a result, in the broad regime with strong correlation, the carrier type in the valence moir´e band is electron-like rather than hole-like.

A more interesting feature in Fig.2(b) is the contrasting behavior between positive and negative displacement fields.For correlated insulators at commensurate fillings (vs=-1,-2),at positiveDthere are correlated gaps(blue),but at negativeDthey are reset (magenta).To check the details, we selectD=±0.6 V/nm and plot filling factorvH(right axis)and Hall resistanceRH(left axis) in Figs.2(c)–2(d), respectively.Corresponding to the colored lines in Fig.2(b),shaded regions are highlighted.Obviously,in Fig.2(c)the correlated gap ofvs=-2 must emerge beforevsreaches-2,because atvs=-1.5 a new band edge already appears and the sign of the band curvature(hence carrier type)is changed to be opposite owing to the correlated gap.In contrast,in Fig.2(d)the carrier type is always electron whenvspasses VHS at-0.5 V/nm,indicating that the flavor polarization and correlated gap atvs=-1,-2 only appear whenvsreaches-1 and-2.Following the Stoner criteria,DOS(ρ)and/orUseems to be greater at a positiveDthan a negativeD,so that the flavor polarization can occur earlier in the former.However,in Fig.1(d)stronger correlated insulator at a negativeDsuggests a largerU.In general,a positiveDwould push electrons to the bottom layer of ABC-TLG.The holes reside further away from the moir´e interface for a positiveDthan a negativeD, thus the latter is experiencing stronger potential modulation from the top hBN.As a result,the negativeDhas a larger superlattice bandgaps atvs,i.e.,the band is better isolated.Without band isolation,the thermally excited or disorder-scattered carriers from the lower bands would suppress the ordering of the electrons and hence the correlated states,[43]which may explain the more resistive correlated peak at a negativeD.Whether the stronger modulation further flattens the moir´e band at the negativeDremains in debate.[15,44]We leave the question about whichDhas a largerUto the future.

At last, we would like to propose a filling sequence for each case.In general, there are two kinds of moir´e superlattice, one is thought to be strong modulation in homo-bilayer such as twisted bilayer graphene, the other is weak modulation from distinct constituent layers such as graphene and hBN heterostructures.In the latter systems,e.g.,a rhombohedral trilayer graphene superlattice studied in this work,moir´e potential is suggested to play a minor role in determining electronic ground states.[15]It was shown that in pristine trilayer graphene,due to the strong electron-correlation induced flavor polarization,the filling sequence is a single spin–valley polarized flavor at the beginning,then two valleys of the same spin and finally four degenerate flavors.[15]So in the cartoon on top of both Figs.2(c)and 2(d),we follow such a filling sequence,but with a difference of when the correlated gap emerges.Note that here electron and holes are denoted by red and blue colors, respectively.To represent the carrier type on the Fermi surface,deep red/blue are used;In other scenarios,e.g.,a flavor is fully filled by electron/hole,light red/blue are plotted.

The above picture is based on the capacitance measurement results[15]of both moir´e superlattice and moir´eless ABCTLG, where one can assume that the moir´e potential modulation does not change flavor symmetry-breaking phases in its moir´eless counterpart.The assumption is also supported by the observation of Chern numberC=-2, 0 atv=-1,-2,respectively.[11]The former indicates the population of a single spin–valley flavor, coinciding with the quarter metal;the latter means the occupation of valley-unpolarized flavors,consistent with the spin-polarized half metal.However, direct verification of the nature of flavor polarization, which needs a high-quality sample to observe quantum oscillation,is yet to be realized.[15]Such an effort deserves more investigation,because recent theories raised a distinct point of view:[44]The graphene/hBN superlattice should not be described by weakly coupled itinerant electrons that exhibit flavor polarization and band reconstruction by the moir´e potential; in contrary, a strong-coupling renormalization of electronic band is required.

4.Quantum Hall ferromagnetism driven by electric fields

Similar to van Hove singularity,Landau levels may also lead to a substantial density of states.Following the Stoner criteriaρU>1,both can invoke flavor polarization because of the gain in exchange exceeding the cost in kinetic energy.Mimicking the spin polarization induced ferromagnetism,flavor polarization within LLs is termed as quantum Hall ferromagnetism.[45,46]

Here in a rhombohedral trilayer graphene, LLs’ energies follow:[46–49]EN=±[(2FeB)3/2)/(γ21)][N(N-1)(N-2)]1/2, whereNis an integer denoting the LL index,eis the electron charge,vF∼106m/s is the Fermi velocity of single layer graphene,γ1is the interlayer hopping energy, andhis Planck’s constant.Without correlation induced symmetry breaking, LLs ofN=0, 1, and 2 are degenerate.Including the spin and valley degrees of freedom,it yields a 12-fold degeneracy for the lowest LL.This is exactly what we observe in Fig.3(a).AtB=3.5 T, the energy interval between LLs is, to some extent, smeared by disorder and thermal fluctuation,thus the overlap of broadened LLs reduces the electronic correlation.As a result, the orbital degeneracy forN=0, 1,2 is preserved.In contrast, the spin degeneracy is lifted by theBfield and the valley degeneracy is broken by theDfield.The latter is due to that valley degree of freedom is locked to layers in real space for zeroth Landau levels in graphene.Obviously,atD=0 V/nm the gapped ground state at CNP is spinpolarization(blue shaded region in the right panel of Fig.3(a));with increasingDthe LLs cross each other and enters into another gapped state that is of valley polarization (shaded in yellow).Such a spin-to-valley polarization transition is also observed for a larger orbital numberN>2, in which the total degeneracy is four hence the mechanism is straightforward(Fig.3(c)).Note that in Figs.3(c) and 3(d), instead ofvswe use the Landau level filling indexvLL=n/(B/Φ0),whereΦ0is flux quanta.

TheD-driven spin-to-valley polarization becomes more complicated when more symmetry breaking is involved.As shown in Fig.3(b), the increasingBfield renders an LL further apart in energy from adjacent LLs, hence electronic correlation is enhanced.A direct result is the lifting of orbital degeneracy.The simple line crossing(Fig.3(a))now becomes a matrix(Fig.3(b)).

5.Discussion

In this work, various symmetry-breaking processes between spin and valley flavors are unveiled in a rhombohedral trilayer graphene superlattice.When the displacement field is sufficiently large, the flattened band dispersion is enough to give rise to an ultrahigh density of states to fulfill the requirement of Stoner criteria.Consequently, we can observe spontaneous symmetry breaking and flavor polarization.Around zeroD,however,one needs to introduce Landau levels of narrow bandwidth to break spin,valley,and orbital degeneracies.Despite the common points for all the transitions,we note that the different details provide valuable insight to the process of when and how the flavor symmetry is broken.Such information is expected to help understand the ground states of exotic quantum phases in fast growing Moir´e superlattice systems.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.11974027 and 62275265), the National Key Research and Development Program of China(Grant Nos.2019YFA0307800 and 2021YFA1400100), and Beijing Natural Science Foundation(Grant Nos.Z190011 and 4222084).