大洋钻探井口吸入模块设计与模态分析

王嘉瑞，秦如雷*，冯起赠，陈浩文，许本冲，卢秋平，刘晓林

（1.中国地质科学院勘探技术研究所，河北 廊坊 065000； 2.中国地质调查局广州海洋地质调查局，广东 广州 510075）

0 引 言

大洋钻探始于1988 年，在验证地球深部岩石循环和板块构造、提高古气候重建准确性、发现深部生物圈和油气矿产资源、防灾减灾等方面发挥重大作用，而海洋水深超过2000 m 的深海占地球表面的2/5，随着大洋钻探逐渐向深海发展，也遇到了诸多难题［1-6］。双梯度钻井（Dual Gradient Drilling，简称DGD）技术可解决部分深海钻探难题，技术核心可以理解为释放单一梯度钻井中隔水管内泥浆（密度大于海水）引起的井底压力过大，有效匹配地层孔隙压力和破裂压力间隙［7-11］。无隔水管泥浆闭式循环钻井（Riserless Mud Recovery Drilling，简称RMR）是双梯度钻井方法的其中一种，该方法不采用隔水管，通过井口吸入模块（Suction Module，简称SMO）将返回的岩屑和钻井液分流出来，经过海底泥浆举升泵（SPM）和回流管线（MRL）从海底返回至钻井平台，从而实现钻井液循环［12-16］，结构示意如图1 所示，无隔水管泥浆闭式循环钻井与常规隔水管钻井的压力梯度对比如图2 所示。

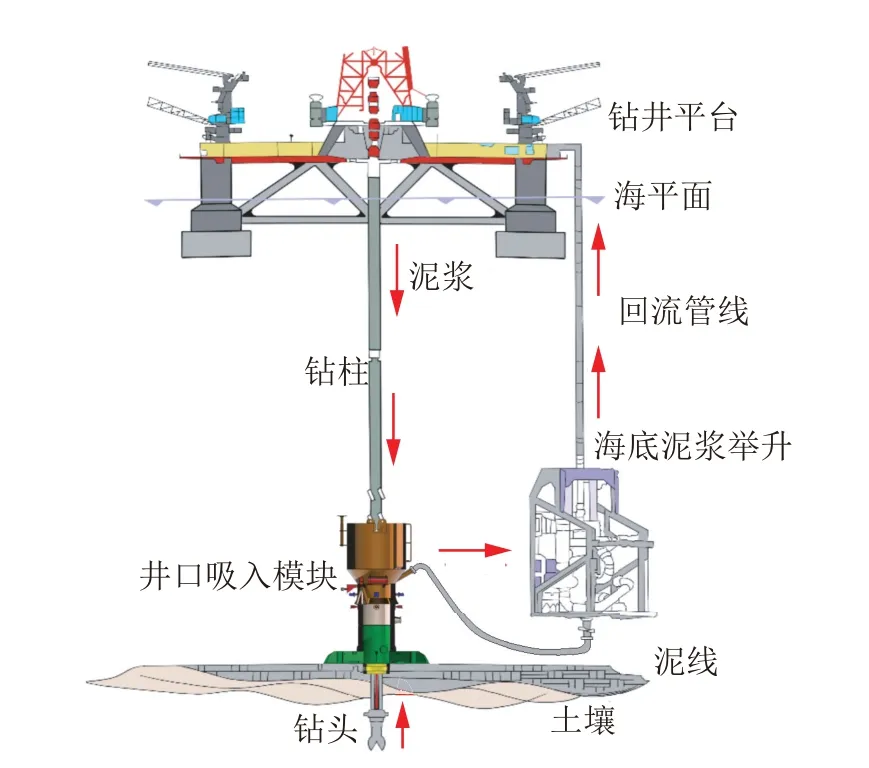
图1 无隔水管泥浆闭式循环钻井系统结构示意Fig.1 Structure diagram of the RMR system

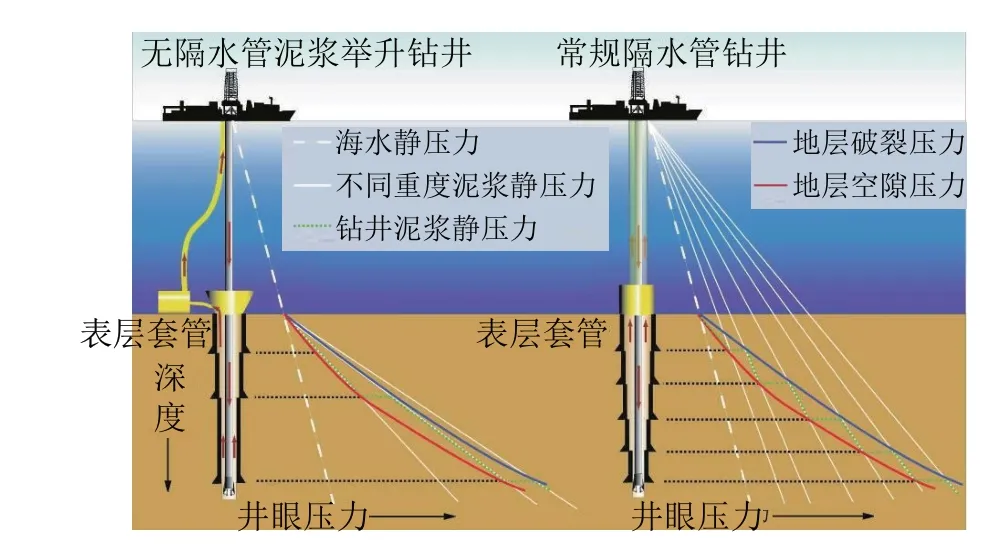
图2 无隔水管泥浆闭式循环钻井与常规隔水管钻井的压力梯度对比[17-18]Fig.2 Comparison of pressure gradient between RMR and conventional riser drilling

井口吸入模块（SMO）是无隔水管泥浆返回钻井系统中的关键组成部件，其主要功能是扶正下入钻具、为钻井液返回管线提供接口以及隔离环空顶部和周围海水环境。国外井口吸入模块的研究起步较早，2006 年，在库页岛大陆架上使用RMR 技术时，SMO 上端采用开放式，装有压力传感器和摄像机用于监测泥浆液位，调节泥浆举升泵转速控制泥浆液位［19-20］。2006—2009 年，为了使RMR 与套管钻井结合，对SMO 进行设计修改，在SMO 底部安装可打开的井口适配器形成更大的内径，使高压井口顺利通过，并在澳大利亚近海的Dampier 次盆地成功应用［21］。2008 年，在马来西亚沙巴洲近海进行深水钻井试验，通过遥控无人潜水器（Remote Operated Vehicle ，简称ROV）将SMO 安装在低压井口，摄像机、压力传感器和电子舱等电子设备与本体分开下放，本次实验验证了1419m 深水的可行性［22］。2009 年在墨西哥湾使用RMR 技术时，下放SMO 到大口径低压井口，SMO 和钻杆尾部采用了专用的J形槽进行连接，可配备内部低压井口适配器或外部适配器［23］。2011 年，在巴西近海钻井时使用了一种新设计的SMO，SMO 与贯入桩同时下入海底，海底泵模块通过导丝下入并安装在SMO 顶部，可进行开放水域下套管，导管柱与海底泵之间通过软管连接，改进后的RMR 系统可以提高钻井效率［24］。2018 年，在巴伦支海应用RMR 技术，并对SMO 进行了相关改造，为了在固井作业中建立循环系统，SMO 适配器上安装了管线、阀门和密封件，以密封井口上的水泥端口，从而在高压井口降落到低压井口后形成闭环循环系统［25］。

国外井口吸入模块通过反复应用进行了多项改进与迭代升级，国内的井口吸入模块大多停留在理论研究和初期研发阶段。2010 年，中国石油大学（华东）陈国明教授团队的刘杰［26］、徐群［27］对SMO进行初期设计，并参考AGR 公司的三代SMO 开发出了数字样机，为SMO 的国产化设计和应用提供参考。2013 年，刘玉亮［28］对SMO 关键部件进行耐久性分析和设计，对密封胶芯进行ABAQUS 分析，提高了SMO 的工作性能和适用性。2019 年，王志伟［29］设计了一种井口吸入模块旋转密封总成下放回收装置和液压锁紧装置，并对其进行了强度评估，陈国明教授团队基于海底泥浆举升技术，形成了吸入模块样机、圆盘泵组及返回管线的室内试验系统，并进行了相关控制系统的设计。本文根据井口吸入模块的使用条件进行设计，建立三维模型，对结构进行了静力学分析和模态分析，为后续井口吸入模块研发提供参考，为大洋钻探向深海发展提供技术支撑。

1 井口吸入模块设计

1.1 条件方案

针对中国南海特有的强热带风暴、内波流等复杂的气候条件，给出本次井口吸入模块设计的条件参数，详见表1。

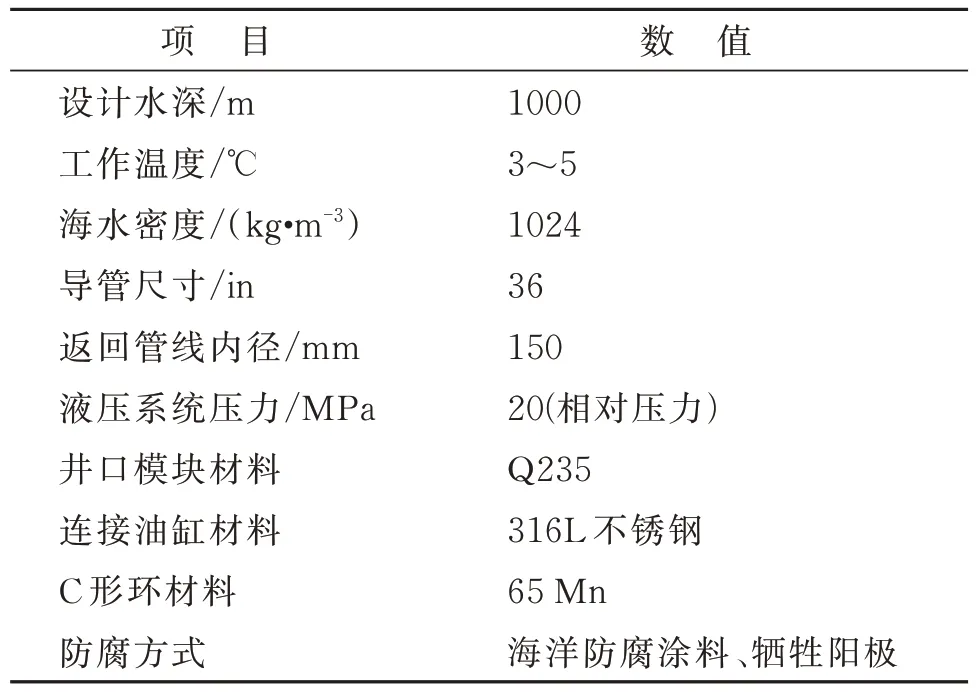
表1 井口吸入模块条件参数Table 1 Condition parameters of wellhead suction module

钻井作业时，先将C 形环装入连接短节卡槽内，连接短节与低压井口和36 in（Ø814.4 mm）导管焊接，焊接后慢速下放导管组焊件使其与泥垫通过C形环卡住，球阀穿过井口模块圆孔与低压井口头连接，即可按照常规导管下放程序布放井口模块，施工完毕后，将井口模块专用J 形打捞工具通过钻杆下入至井口模块指定处，通过井口模块自带摄像头与ROV 观察连接情况，将ROV 上的Hotstab 公头与井口模块上的母头连接，使用ROV 的液压供液功能驱动连接油缸回收，提起打捞工具完成井口模块上下分离并进行回收，结构示意如图3 所示。

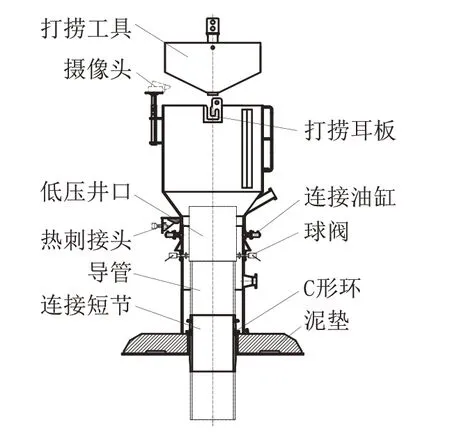
图3 井口吸入模块结构示意Fig.3 Structure diagram of wellhead suction module

井口吸入模块上端可采用开放式，也可采用旋转密封式，当发生浅层气溢出情况时，开放式井口吸入模块中的泥浆与海水相通，溢出的气体可直接进入海水，旋转密封式井口吸入模块则会使气体通过泥浆循环系统涌入钻井平台，存在安全隐患。开放式顶部摄像头可实时观察井口情况，通过调整海底泵组转速控制泥浆线位置，维持井内压力稳定，不必担心泥浆溢出情况，试验中摄像观察到泥浆与海水可保持界限分明［17，20］。

1.2 结构设计

根据条件方案，结合1000 m 左右水深的钻井作业环境和海洋钻井工作流程，研究功能需求，本着“简单、经济、够用”原则设计井口吸入模块，三维模型如图4 所示。

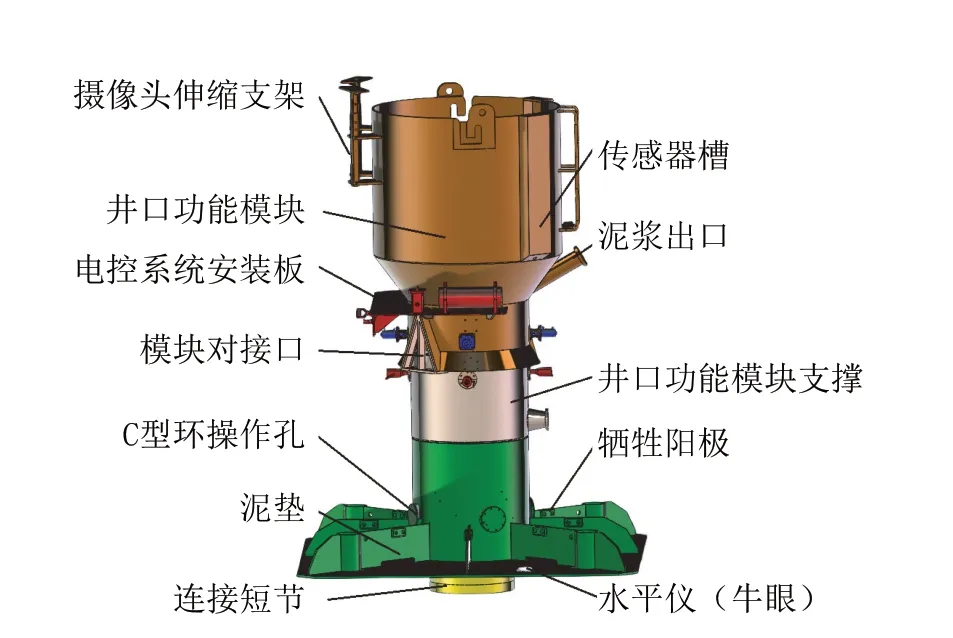
图4 井口吸入模块三维建模Fig.4 3D modeling of wellhead suction module

2 井口吸入模块静力学分析

井口吸入装置在海底的受力情况如图5 所示。在泥线以下的导管受到泥土对导管的反作用力，该力在进行分析时采用弹簧阻尼器来等效，根据不同深度的泥土采用不同刚度的弹簧进行模拟。泥线以上的部分即为井口吸入装置，该部分主要受到海底波流力，根据受力情况对该模块进行整体静力学分析以及模态分析［30-32］。采用ABAQUS 仿真软件对井口吸入模块整体结构进行静力学分析。海洋的波流力由莫里森公式计算得出，而后加载在井口吸入装置的外圆柱面上，以此来等效。

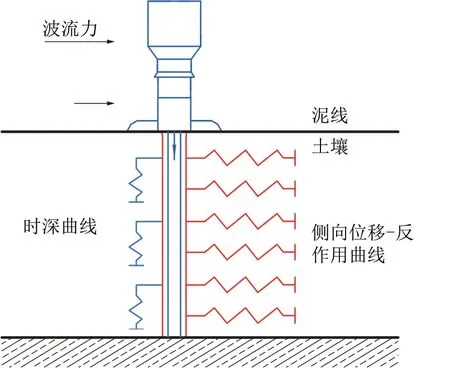
图5 井口吸入模块受力情况示意Fig.5 Diagram of force condition on wellhead suction module

2.1 莫里森方程

对小构件，即构件直径与入射波的波长相比尺度较小的结构物，常采用莫里森等提出的方法计算波流力［33］。莫里森方程以波流质点速度、加速度和柱体直径为参数计算各水深处波流力，然后沿柱长积分得到桩柱波流力［34］。

莫里森等认为作用于柱体任意高度z处的水平波流力f包括2 个分量：

（1）水平拖曳力fD——波流水质点的水平速度ux引起的对柱体的作用力：

式中：fD——水平拖曳力，N；CD——拖曳力系数；ρ——海水密度，kg/m3；A——单位柱高垂直于波向的投影面积，m2；ux——波流水质点的水平速度，m/s。

（2）水平惯性力fI——水质点运动的水平加速度ux引起的对柱体的作用力：

式中：fI——水平惯性力，N；CM——惯性力系数；ρ——海水密度，kg/m3；V0——单位柱高柱体体积，m3；ux——波流水质点的水平速度，m/s。

对于本次对井口吸入装置的分析，根据表2，由于井口吸入装置处于1000 m 的海底，故拖拽力系数CD取0.7；海水密度ρ取1024 kg/m3；取某工区深度为1000 m 以及海洋流速为0.49 m/s，故波流水质点的水平速度ux取为0.49 m/s。根据井口吸入模块的设计尺寸及投影面积可求得：最上部圆柱面所受水平拖拽力约为255.79 N，中间圆锥所受水平拖拽力约为72.41 N，下部圆柱面所受水平拖拽力约为306 N。由于分析所取流速为均匀流速，故井口吸入装置不受洋流的水平惯性力。

表2 水动力参数[35]Table 2 Hydrodynamic parameters

2.2 仿真分析前处理设置

井口吸入装置和导管的材料都采用Q235，该材料的密度为7850 kg/m3，杨氏模量为210 GPa，泊松比为0.3，将以上材料属性赋予分析模型。本次分析是对井口吸入模块整体结构的静力学分析，故分析类型选择静态、通用。对于该井口吸入模块，选择划分网格的单元形状为四面体，划分技术采用自由划分，网格划分算法采用默认算法，由于该模块存在小部件，故对于小部件还应采用局部划分，设置更精细的局部网格以保证完全划分，划分结果如图6所示。

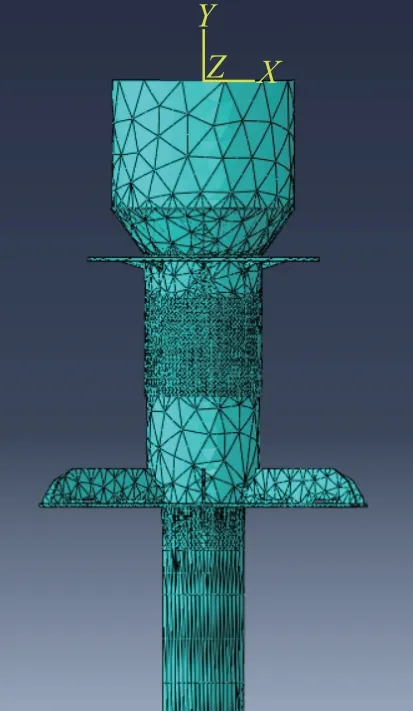
图6 网格划分Fig.6 Mesh division

根据莫里森公式算出的水平拖曳力，将该力分别加载到圆柱和圆锥面上。在实际应用中导管深入泥土90 m，导管最底部可视为固定约束，故可对导管最底部设置完全固定约束。由于泥线以下的导管受到泥土对导管的反作用力，在ABAQUS 中该力可在相互作用模块中采用将导管连接弹簧的方式等效处理。故对该模块进行分析时还需对导管设置相互作用，根据不同深度的泥土所绘制出的P-y曲线来得到不同深度的泥土的等效弹簧刚度。将这些不同刚度的弹簧施加在相对应深度的导管上。

P-y曲线法是指在水平力F的作用下，土下深度x处土反力P与该深度结构物侧向变形y之间的关系曲线。它综合反映了桩周土的非线性、桩的刚度和外荷作用的性质等特点，是一种弹塑性分析方法。P-y曲线法不仅适用于静载荷和循环载荷，而且也适用于结构物的大位移和小位移，避免了单一参数法的缺点，已经广泛应用于石油海洋工程中。所涉及到的粘土的主要物理力学性能指标有土的不排水抗剪强度、重度和主应力差［36-37］。

2.2.1 软粘土中的P-y曲线

对于不排水抗剪强度Cu≤96 kPa 的软粘土，泥线x深度下单位桩长的极限土阻力Pu由式（3）确定：

式中：γc——泥线下深度x处土的单位有效重度，kN/m3；Cu——土的不排水抗剪强度，kPa；x——深度，m；D——结构物的直径，m；ξ——无因次经验常数，其值在0.25～0.5 之间，土硬取小值；xr——极限水平承载力的转折点深度，m，通常认为xr范围以内的为浅层土，xr以下为深层土。

（1）软粘土在静载荷下的P-y曲线可由式（4）确定：

式中：P——泥线下深度x处结构物发生横向位移y时，结构物横向极限土阻力，kPa；y——泥线下深度x处构物发生横向位移，m；y50——横向土阻力为极限横向土阻力一半时，结构物的横向位移，m；ξ50——原状土不排水试验中1/2 最大应力处发生的应变，可由表3 确定。

表3 软粘土ξ50值[38]Table 3 ξ50 value of soft clay

（2）软粘土在循环载荷下的P-y曲线：

当x＜xr时，侧向极限土阻力可由式（5）确定：

当x>xr时，侧向极限土阻力可由式（6）确定：

2.2.2 硬粘土中的P-y曲线

对于不排水抗剪强度Cu>96 kPa 的硬粘土，用式（3）分别计算，取小值作为单位结构件上极限土阻力Pu。

横向土阻力为极限横向土阻力一半时结构物的横向位移由式（7）确定：

其中ε50的值通过现场试验确定，若条件不够则通过表4 确定。

表4 硬粘土ξ50值[38]Table 4 ξ50 values of hard clay

（1）硬粘土在静载荷下的P-y曲线可由式（8）确定：

（2）硬粘土在循环载荷下的P-y曲线可由式（9）确定：

式中：N——循环载荷施加次数；yc——N次循环加载后的位移，m；ys——短期静载荷下的位移，m；y50——相应于极限土阻力一半时的短期静载位移，m。

对每一处深度下硬粘土，可通过上式求得对应P-yc曲线。某工区海底深度37 m 内是软泥土，37～90 m 是硬质粘土，土壤基本数据见表5，根据土壤实测数据可得出各离散层处土壤的P-y关系，进而得出不同深度的泥土的等效弹簧刚度。

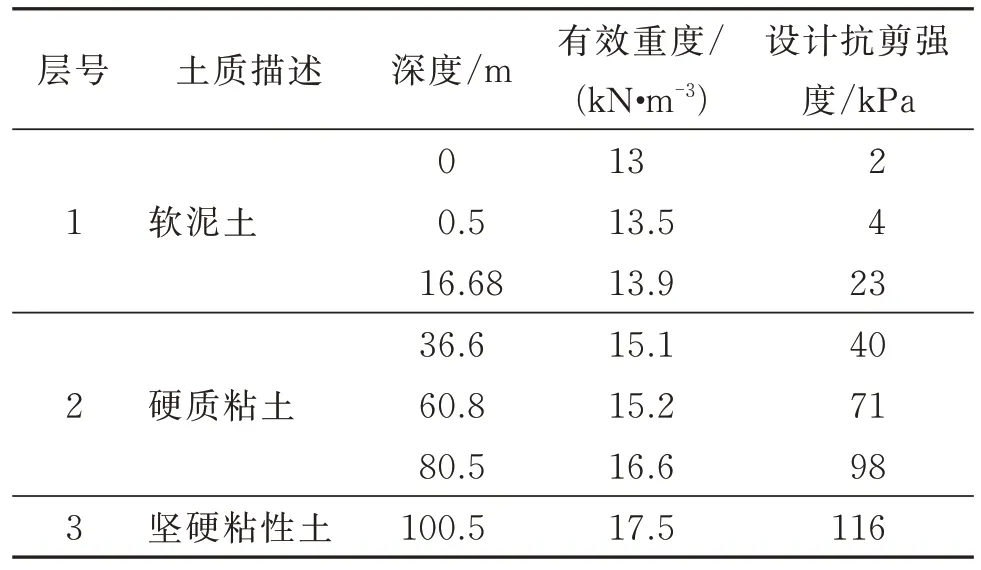
表5 某工区土壤基本数据Table 5 Soil basic data

2.3 井口吸入模块整体结构力学特性分析

根据波流力和泥土对井口吸入模块连接导管的反作用力，可得出井口吸入模块应力云图如图7 所示，井口吸入装置最大应力发生在底部筋板与圆柱结合处，其值约为7 MPa，由于材料Q235 屈服强度为235 MPa，故该井口吸入模块满足强度要求，安全系数可达到33。井口吸入模块应变云图如图8 所示，井口吸入装置最大应变发生在底部筋板与圆柱结合处，其值约为2.8×10-5mm，该值较小，井口吸入装置能满足正常工作。井口吸入模块位移云图如图9 所示，井口吸入装置最大位移发生在最顶部，其值约为0.17 mm，该值较小，井口吸入装置能满足正常工作。

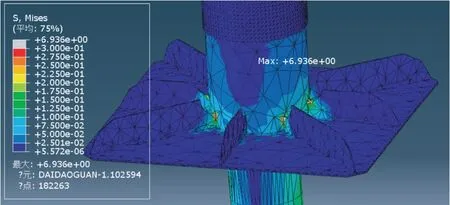
图7 井口吸入装置应力云图Fig.7 Stress nephogram of wellhead suction unit

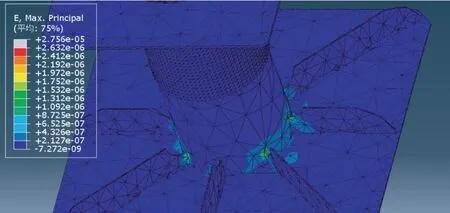
图8 井口吸入装置应变云图Fig.8 Strain nephogram of wellhead suction unit

图9 井口吸入装置位移云图Fig.9 Displacement nephogram of wellhead suction unit

2.4 井口吸入模块连接部位的应力应变状态分析

井口吸入模块连接部位应力云图如图10 所示，连接部分最大应力发生在小孔处，其值约为43.31 MPa，连接部分所采用的材料为Q235，其屈服强度为235 MPa，远大于连接部分的最大应力，故该连接部分连接可靠。井口吸入模块连接部位应变云图如图11 所示，最大应变同样发生在小孔处，其值约为2.1×10-7mm，该值极小，可忽略不计，故该连接部分连接可靠。

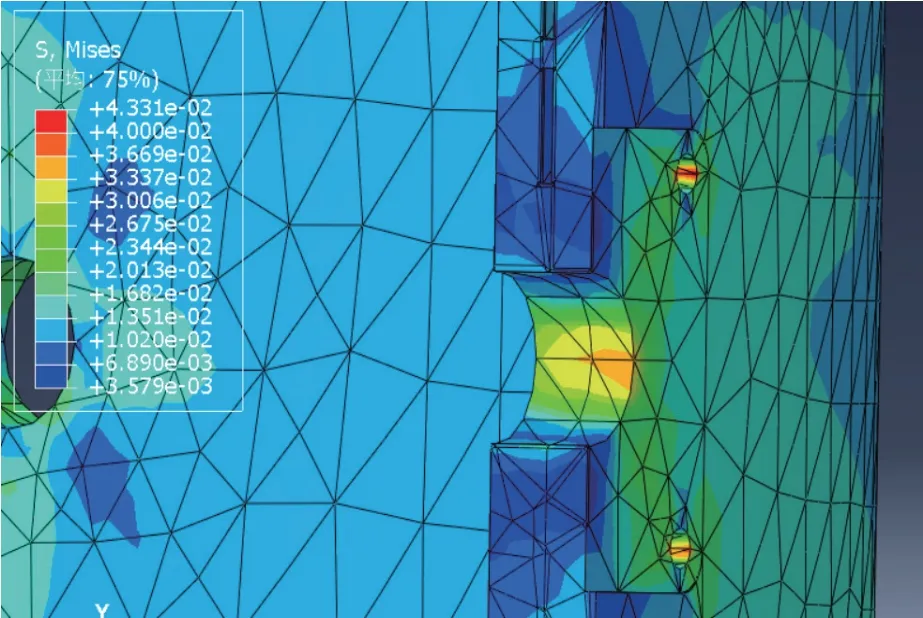
图10 连接部位应力云图Fig.10 Stress nephogram at the connection part

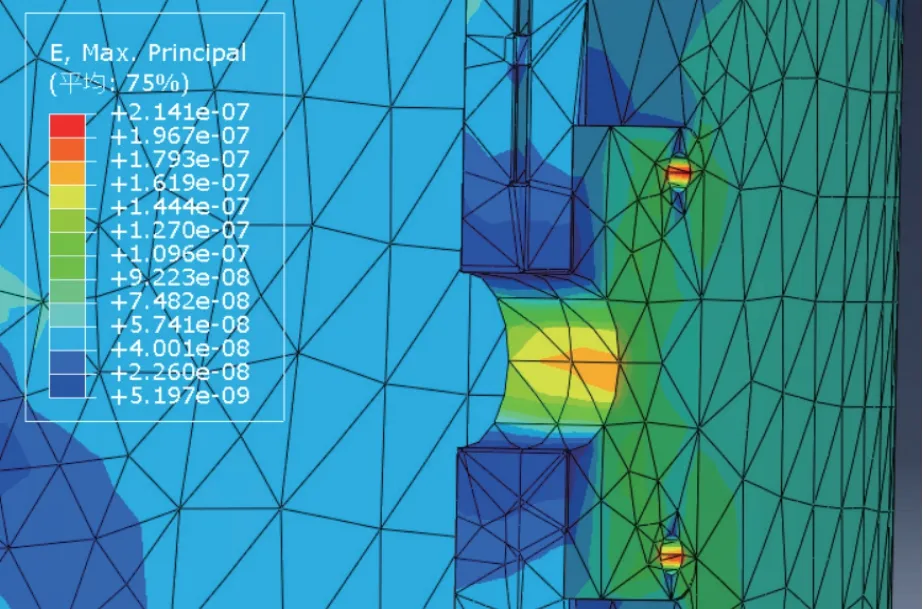
图11 连接部位应变云图Fig.11 Strain nephogram at the connection part

3 井口吸入模块模态分析

3.1 模态分析前处理设置

对于模态分析，其前处理设置与静力学分析基本相同，不同处有以下2 点：模态分析的分析步类型采用的是线性摄动中的频率分析，而静力学分析的分析步类型采用的是通用中的静力分析；模态分析不需要施加载荷，而静力学分析需要对模型施加载荷［39］。

3.2 模态结果可靠性分析

在使用振型叠加法分析动态问题时，要保证在频率提取分析过程中提取了足够数量的模态，其判断标准是在主要运动方向上的总有效质量要超过模型中可运动质量的90%。对于本次分析，整体模型的主要运动方向为Z轴，从表6 的数据可以看到在Z方向上总的有效质量为84.101 t，而模型的总质量为86.79435 t，所占比例为97%，因此取20 阶振型是足够的，所得结果可靠。

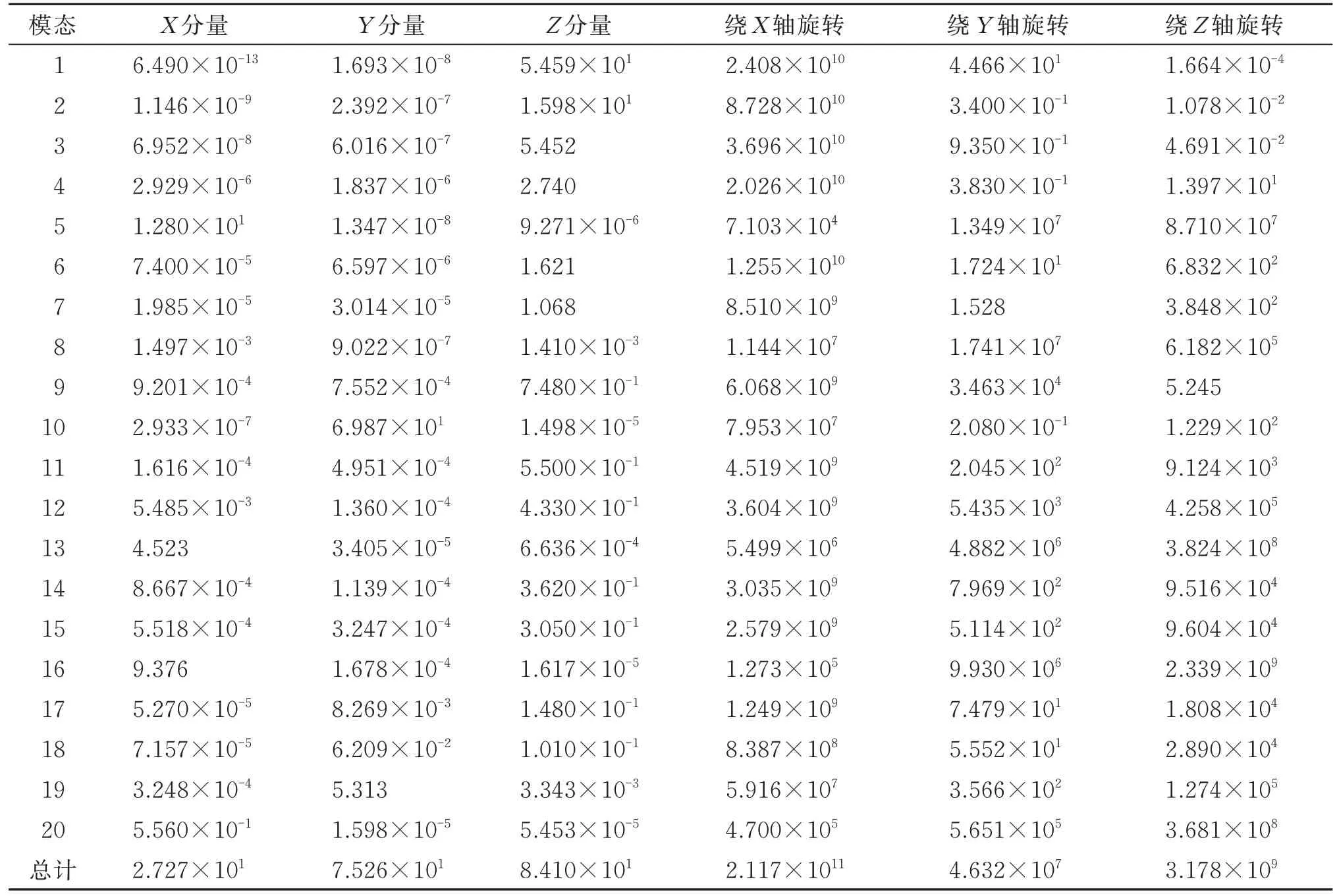
表6 有效质量Table 6 Effective masst

3.3 模态分析结果

由于海洋波流频率很小，其频率大多数情况下≯2 Hz，故只需分析固有频率在2 Hz 内的振型，由表7 可知，频率在2 Hz 以内的阶次为1～3 阶。从表8 所示的参与系数可知，在1～3 阶振型中，Z方向的位移起主导作用，故1～3 阶振型中，模型的主要变形为Z方向的位移，这从1～3 阶振型图（图12～14）也可看出，因此，若在Z方向上有一个接近1～3 阶频率中任意一个频率的激励，可以认为这个结构有发生共振破坏的可能。

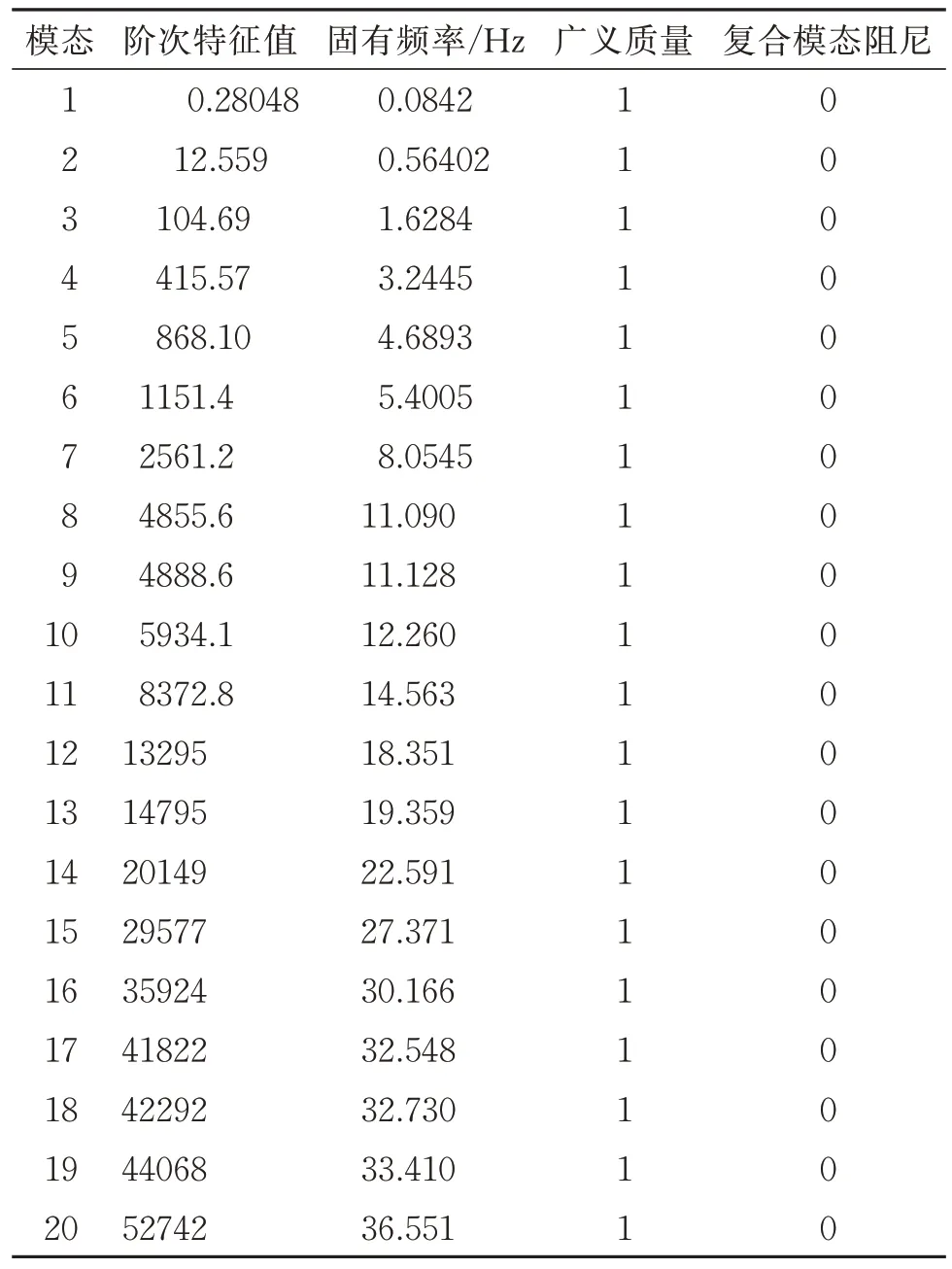
表7 特征值输出Table 7 Eigenvalues output

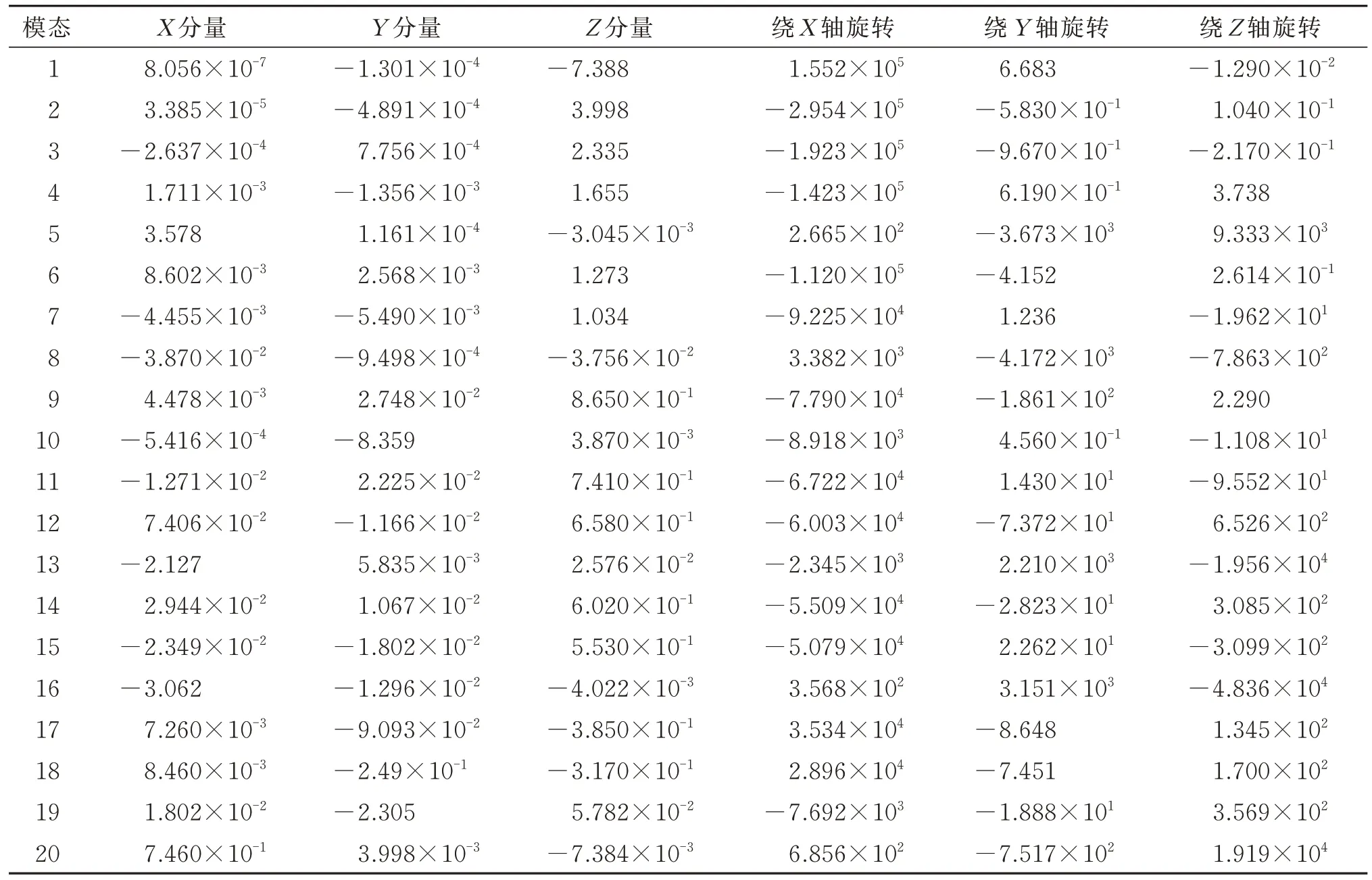
表8 参与系数Table 8 Participation factors

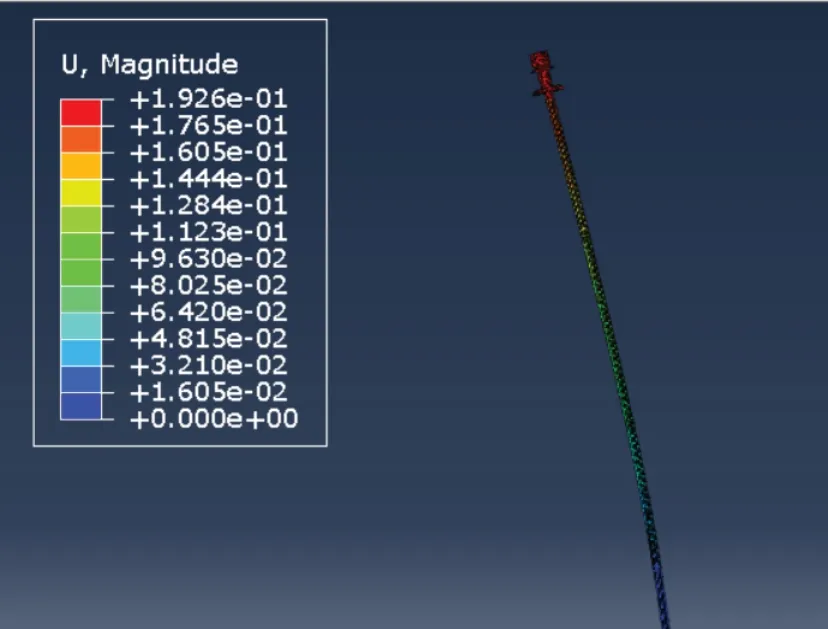
图12 1 阶振型Fig.12 1-order mode diagram

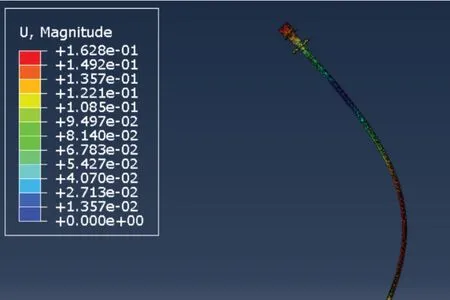
图13 2 阶振型Fig.13 2-order mode diagram

图14 3 阶振型Fig.14 3-order mode diagram

4 结论

（1）井口吸入模块受到海底波流力时最大应力和应变集中在底部筋板与圆柱连接处，分别为7 MPa 和2.8×10-5mm，最大应力值及应变值都不大，对井口吸入模块正常工作影响很小。井口吸入模块受到海底波流力时最大位移在最顶部，为0.17 mm，相对于整体装置>90 m 的长度，该位移对井口吸入模块正常工作影响不大。井口吸入模块连接部位的应力应变分别为 43310 Pa 和2.1×10-7mm，两者都很小，连接部位连接可靠。

（2）与海底波流力频率相接近的频率为1～3 阶模态分析的频率，分别为0.084、0.56 和1.63 Hz，若实际情况下的内波流频率与1～3 阶频率中任意一个频率很接近，可改变井口吸入模块的材料或者尺寸，从而改变井口吸入模块的固有频率，使固有频率与实际情况下的内波流频率相差较大，即可避免共振的发生。

（3）本文研究的无隔水管泥浆闭式循环钻井中井口偏移量为0.17 mm，而相关文献［40］中分析正常深水钻井的井口偏移量最小为9 mm，由此可体现出在井口装置的稳定性上，无隔水管泥浆闭式循环钻井相较于正常深水钻井具有明显优势。