2 种邓肯- 张模型对比研究

邓成发，刘检生，王 良

（1.浙江省水利河口研究院（浙江省海洋规划设计研究院），浙江 杭州 310017；2.浙江省水利防灾减灾重点实验室，浙江 杭州 310017；3.余姚市水库管理服务中心，浙江 余姚 315430）

0 引 言

针对土石坝的应力应变分析，国内众多学者常采用邓肯-张E-ν 或E-B 模型[1-5]，同时不少研究者认为E-B 模型优于E-ν 模型，但朱俊高等[6]在对比分析后认为，尽管E-B 模型是在E-ν 模型之后提出，但E-B 模型优于E-ν 模型缺乏理论依据。殷宗泽[7]认为E-B 模型更适合面板堆石坝计算，E-ν 模型则更好地反映出心墙土的泊松比对水力劈裂有显著影响。宿辉等[8]认为小粒径材料（如：土）的计算可采用E-ν 模型，而粗粒材料（如：堆石）的计算采用E-B 模型可能更好一些。

本文通过三轴试验与数值模拟的对比，验证了计算结果与试验值的相符性，同时对比2 种模型的差异，有利于深刻认识2 种模型对土体应力应变特性的反映能力。

1 计算模型

邓肯-张E-ν、E-B 模型均采用双曲线拟合三轴仪轴向偏应力（σ1-σ3）与轴向应变εa关系曲线，并推求出切线弹性模量：

式（1）～（2）中：K、n为模型参数；Rf为破坏比；S为应力水平；c为土体的粘聚力，kPa；φ为土体的内摩擦角，（°）；pa为大气压力，Pa；σ1为轴向应力，MPa；σ3为侧向围压，MPa。

邓肯-张E-ν 模型假定侧向应变εr与轴向应变εa的关系为双曲线，推求出切线泊松比表达式：

式（3）～（5）中：vi为初始泊松比；G、D、F为模型参数。

邓肯-张E-B 模型假定体积应变εv与轴向应变εa的关系为双曲线，从而得到体积模量表达式：

式（6）中：Kb、m为模型参数。

则对应的泊松比ν可表示为：

由此可以看出，2 种模型的差异主要由于泊松比的计算方式不一致。为了研究2 种模型的差异，在一个模型中同时运用2 种材料模型进行计算研究。

2 模型验证

2.1 计算参数

为了直观说明2 种模型的差异，选用双江口堆石坝掺粒黏土心墙料的三轴试验[9]成果进行分析验证。试验仪器为常规中型三轴仪，试样直径10 cm，高度20 cm，试验得到的模型参数见表1。

表1 邓肯-张E-B、E-ν 模型参数表

2.2 模型建立

计算模型尺寸与试样尺寸相同，加载方式同常规三轴试验的加载方式保持一致，即由试样顶部向下逐步施加位移荷载，每步施加0.2 mm，直至达到20 mm（对应的竖向应变为10%）。模型上半部采用E-B 模型，下半部采用E-ν 模型。计算模型单元数为6 400 个，模型网格见图1。

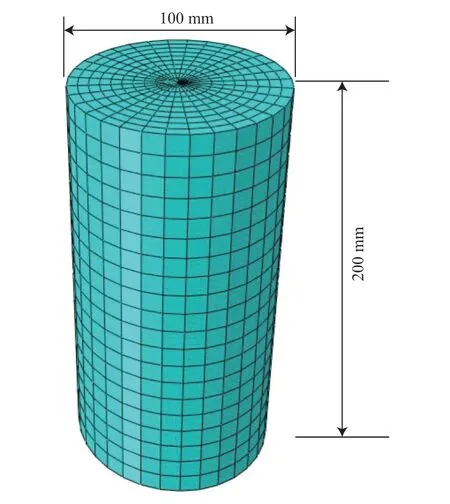
图1 计算模型网格划分图

2.3 模型分析

围压为200、600、1 000、1 500 kPa 时，试样上、下部偏应力（σ1-σ3）与轴向应变εa的关系曲线见图2。由图2 可以看出，上半部分（E-B 模型）和下半部分（E-ν 模型）的偏应力与轴向应变关系曲线基本重合，符合广义胡克定律的一般规律，反映了上、下部土体切线弹性模量的一致性，同时也体现了土体的非线性特征。

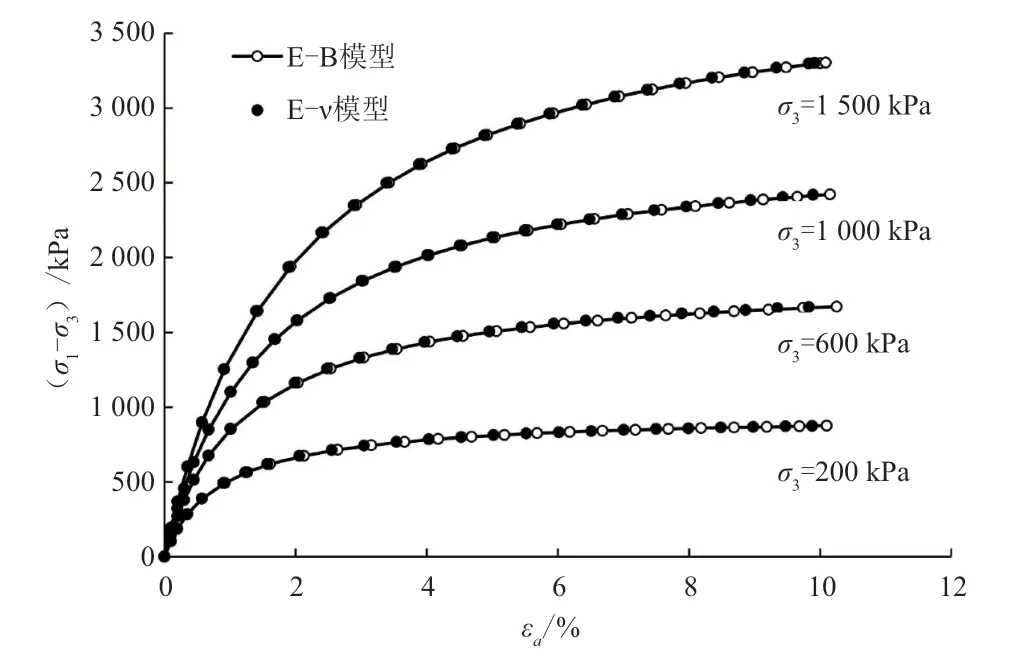
图2 偏应力与轴向应变关系曲线图

偏应力（σ1-σ3）与轴向应变εa关系数值的计算值、试验值对比见图3。由图3 可以看出，计算所得偏应力与轴向应变的关系曲线与试验数据点基本吻合，仅在高围压下误差略有增大，计算结果合理，证明试验曲线与模型参数相符。

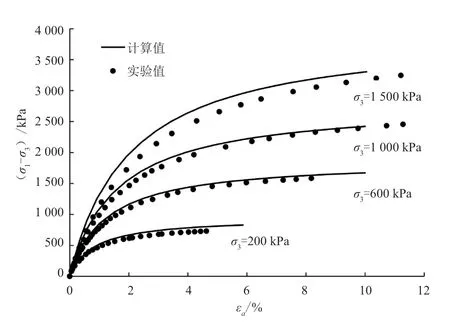
图3 偏应力与轴向应变数值的计算值、试验值对比图

E-ν、E-B 模型体积应变εv与轴向应变εa数值的计算值、试验值对比见图4～5。由图4～5 可以看出，同一围压下，偏应力较小时，E-B 模型的体积应变较E-ν 模型大，且E-ν 模型计算值与试验值吻合度较高，而E-B 模型偏差较大；偏应力较大时，2 种模型的计算值与实验值差异均较大，且E-B 模型的体积应变小于E-ν 模型。相比而言，E-ν 模型较E-B 模型更接近实验值。

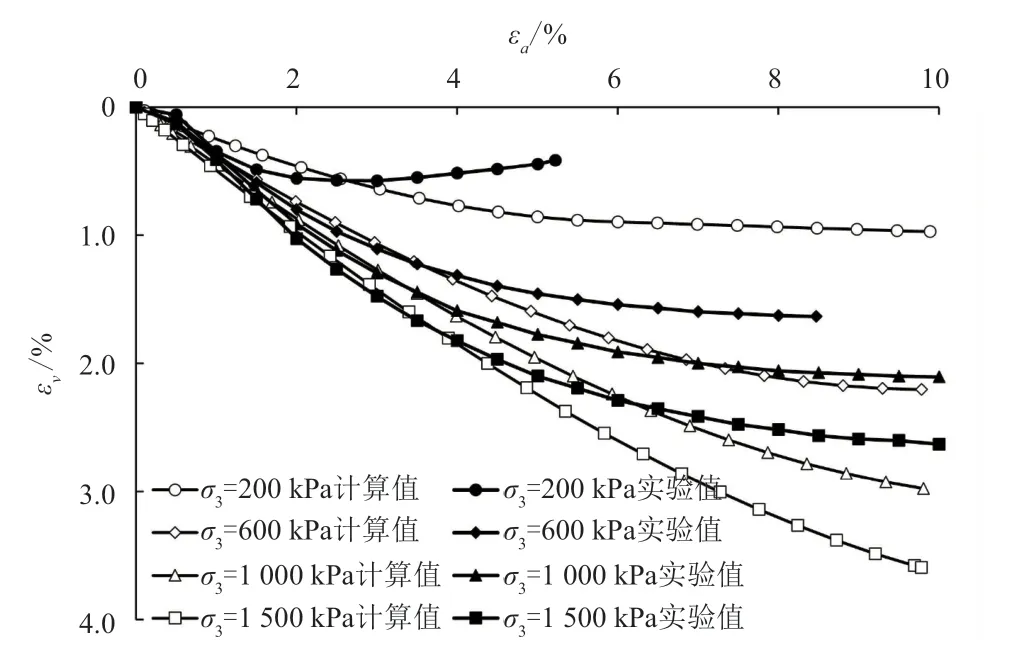
图4 E-ν 模型体积应变与轴向应变数值的计算值、试验值对比图

图5 E-B 模型体积应变与轴向应变数值的计算值、试验值对比图

试样偏应力（σ1-σ3）与侧向应变εr的关系见图6。由图6 可见，侧向应变与偏应力呈双曲线关系。相同围压下，2 种模型的偏应力与侧向应变关系曲线存在1 个交汇点。在交汇点之前，即偏应力较小时，E-ν 模型的侧向应变较E-B 模型大；交汇点之后，即偏应力较大时，E-B 模型侧向应变较E-ν模型大。

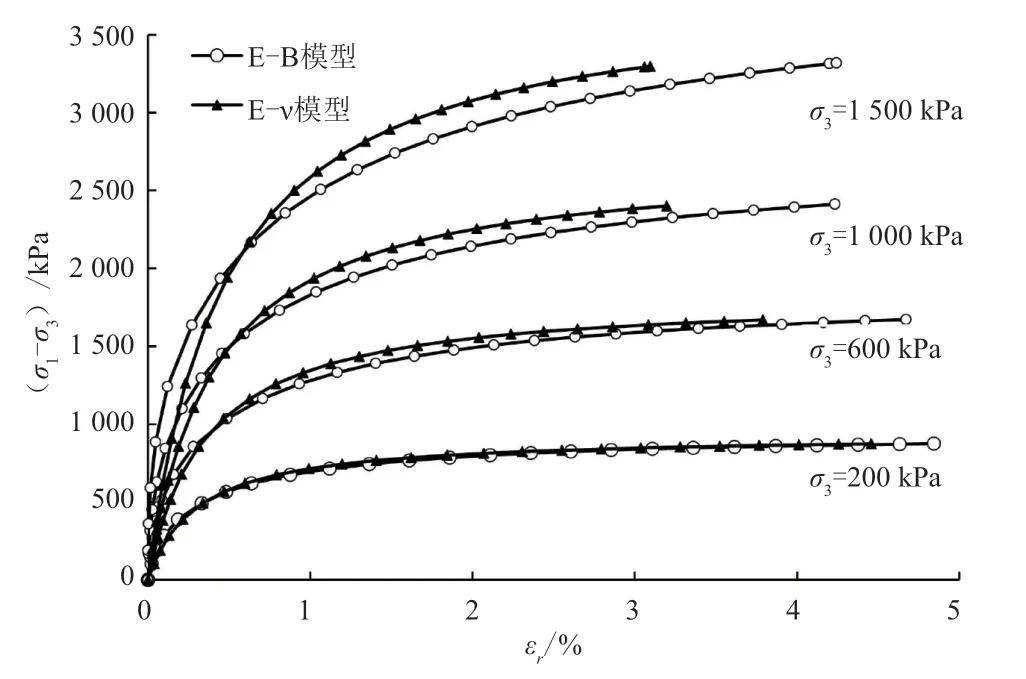
图6 偏应力与侧向应变关系曲线图

当轴向应变达到10%时，试样中部侧向应变εr沿高度方向的变化曲线见图7。由图7 可以看出，同一围压下，E-B 模型的侧向应变较E-ν 模型大；围压越大，侧向应变越小；随着围压增大，2 种模型的侧向应变差异越大。围压为200 kPa 时，E-B 模型的最大应变比E-ν 模型大8.9%；围压为1 500 kPa 时，E-B 模型的最大应变比E-ν 模型大37.8%。

泊松比与应力水平关系曲线见图8。由图8 可以看出，随着应力水平的增加，E-B 模型泊松比基本呈线性增加趋势，而E-ν 模型关系曲线在应力水平较低时变化平缓，仅在高应力水平时曲线渐陡，且围压越小，曲线后期越陡。同一围压下，应力水平较低时，E-ν 模型泊松比较E-B 模型大，应力水平较高时，则相反。围压越大，泊松比越小。

图8 泊松比与应力水平关系曲线图

3 结 论

1）2 种模型的切线弹性模量具有一致性，但泊松比差异显著，随着应力水平的增加，E-B 模型泊松比基本呈线性增加趋势，而E-ν 模型关系曲线在应力水平较低时变化平缓，仅在高应力水平时曲线渐陡，且围压越小，曲线后期越陡。

2）同一围压下，应力水平较低时，E-ν 模型泊松比较E-B 模型大，应力水平较高时则相反。围压越大，泊松比越小。

3）偏应力较小时，E-B 模型体积应变较E-ν模型大，而侧向应变较E-ν 模型小；偏应力较大时则相反。随着围压的增大，2 种模型的体积应变和侧向应变差异越大。总体来看，E-ν 模型较E-B 模型更接近实验值。