基于Excel的p控制图的四种画法

俞钟行

1924年，美国贝尔实验室的工程师休哈特画出全世界第1张控制图——p控制图，从此开启了SPC（统计过程控制）在全球的百年历程。俄罗斯学者阿特列勒和施贝勒对这段历史有一段精彩评价：“统计思维是在一个饱受易变性之害的世界里做出系统性决策的能力（引自《上海质量》文章《从统计思维到智能思维》）。”p控制图即“不合格品率控制图”，因其易懂、易用、灵活，而被广泛应用，比如曾推行14年之久的国家质量工程师职业资格考试中，只有p控制图和Xbar-R控制图被要求达到“掌握”的程度。但是应用p控制图也存在某些问题，本文从贴近企业实际应用的角度，介绍p控制图的4种画法，通过普及程度更高的Excel工具实现。

p控制图的统计基础是二项分布。二项分布只有一个参数，故p图是单图。计算平均不合格率的公式为：

P控制图的3条线的计算公式为：

注意事项：选取样本量n应充分大，使得np0≥1。一般情况下：

这里，P0：给定标准值；pbar：未给定标准值。

p图第一种画法[1]

如果ni变化不大（指ni变化在其目标值±25%以内）,采用单一的基于平均子组大小(nbar)的一组控制限。

例：山东某预制板企业，在国内外均设有工厂，统计部门把各厂采集的数据汇总到经营层。表1左起两列是某厂某月每天的一等品（AA）和二等品（A）的具体数据。A等品相对于AA等品就是不合格品，因此可以画p控制图，这对于提质降本、改善经营有所裨益。

左起第3列n，是1、2列的和，就是样本量。第4列A%相当于不合格品率p%。2至4列的倒数第2行，分别是∑di、∑ni和pbar值。n列最下面的数是nbar。于是可按pbar和本节公式得到表1的右边3列。用Excel的折线图就可画出p控制图，如图1所示。从图1可以看出，如果在月初的3、4天里质量控制得好些的话，这个月的A%可以更低、更平稳些。笔者在上海金山石化公司，也从控制图看到生产刚开始时，产品质量相对差一些。“质量看得见”是控制图的一项优势。

图1 山东某企预制板“A等品率”的控制图

p图第二种画法[1]

当ni变化较大时，可采用标准化变量的方法，如点绘标准化Zi值：

这样，中心线和控制限与子组大小无关，即：

例：上海某避雷器厂，生产的批量产品分大罐和小罐，见表2左起第2列，相当于样本量ni。第3列是检查出的不合格品数di，第4列是不合格品率pi。第2、3和4列最下面的数分别是∑di、∑ni和pbar值。于是，可按Zi公式得到表2的Zi列，用Excel的折线图画出p控制图，如图2所示。从图2可以看出，第4批的不合格品率“鹤立鸡群”，而且远远超出上控制限+3。其实，该批次不合格品率并未超出该厂的有关规定，但是如果有“持续改善”的质量之心，就应当查找这一批次远远超出其他17批次不合格品率的原因。控制图就是可以帮助我们找到改善突破点的好工具。

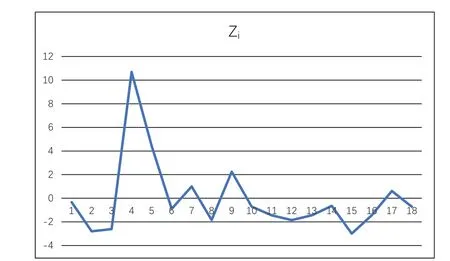
图2 避雷器p控制图（以Zi描点）

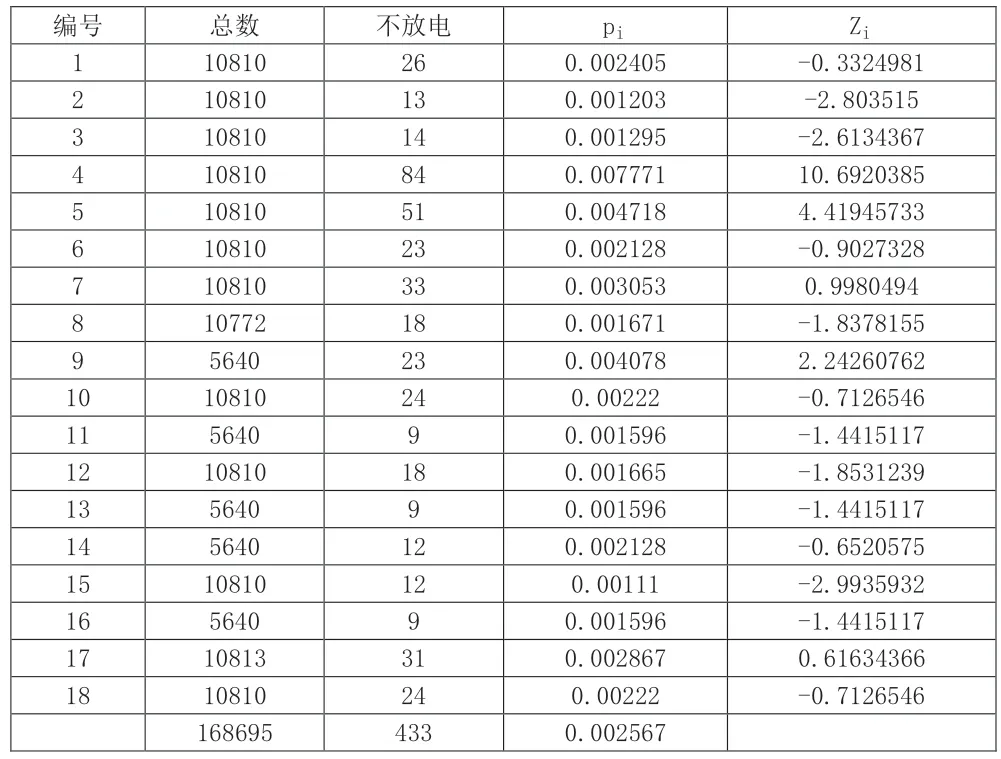
表2 避雷器p控制图（以Zi描点）的数据界面

p图第三种画法

当样本量n i 太大时，前面两种画法都不好使了，原因是对照“注意事项”公式（3），应有n×p0＜5或n×p b ar ＜5的要求。比如表3所示的案例，是转引自Motgomer y（2020）的案例，是某医院在20周内发生错误的记录。经计算，此例的nbar×pbar=2886.2×0.094848=273.7502976，并不符合＜5的一般要求。如果按照第二种方法画p控制图得到的图3，难以反映真实情况。

图3 医院p控制图（以Zi描点）

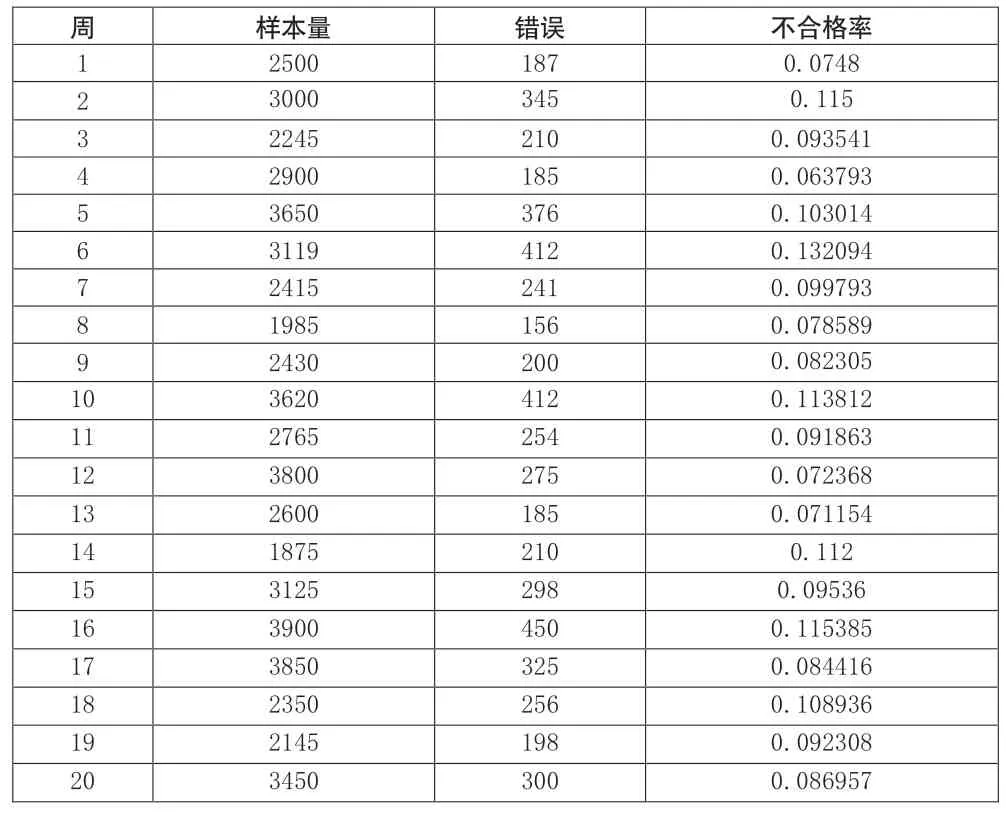
表3 医院p控制图的数据界面

Laney于2002年提出了当样本量很大时画p'控制图的方法，被普遍接受，在Minitab软件里也有这种方法的模块。但是2022年美国质量协会《质量技术》杂志第3期刊登的可公开获取的长文，基于the law of total expectation and the law of total variance（总期望定律和总方差定律）及数据模拟，证明了Laney的p'控制图的不足，并给出了更精准科学的方法。要点是p控制图的变差含有两个普通原因的成份——样本内和样本间，而以前未考虑到“样本间”这一成份。本文将新提出的p控制图称为“双普p控制图”。虽然本文无法介绍这一新方法在“破”和“立”上的诸多细节，但可以用Excel来实现它的最终成果，关键就是算出规定p控制限的σ。

根据文献，这个σ的计算公式如下：

式中的m就是表3中的周数20；p0就是平均不合格品率，已从表3算得，为0.094848。表4左起第2列“分子左”只有是10项，当i=1时，第1项=（p2-p1）2=(0.0748-0.115)2=0.00161604，其余类推。这列倒数第2个数是上述10项之和，最下的数是除以20所得的商。“分子右”这一列里，先按公式[p0(1-p0)/ni]算出第1项，然后用拖拉的方式得到全部20项，倒数第2个数是平均值。“分母右”这一列的计算类似。于是，σ2=（分子左-分子右）/(1-分母右)=0.000362，σ=0.019034。

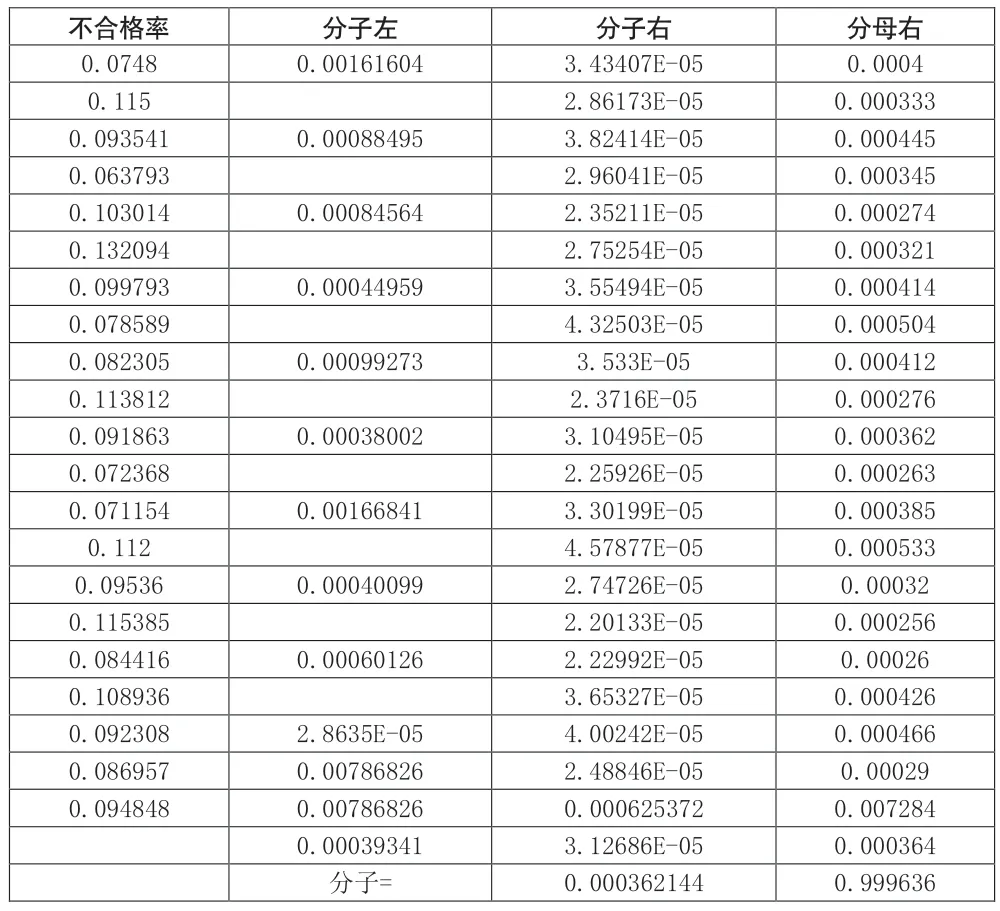
表4 计算σ2的数据界面

然后可以根据文章开始时给出的p控制图3条线的基本公式画出图4，数据界面见表5。

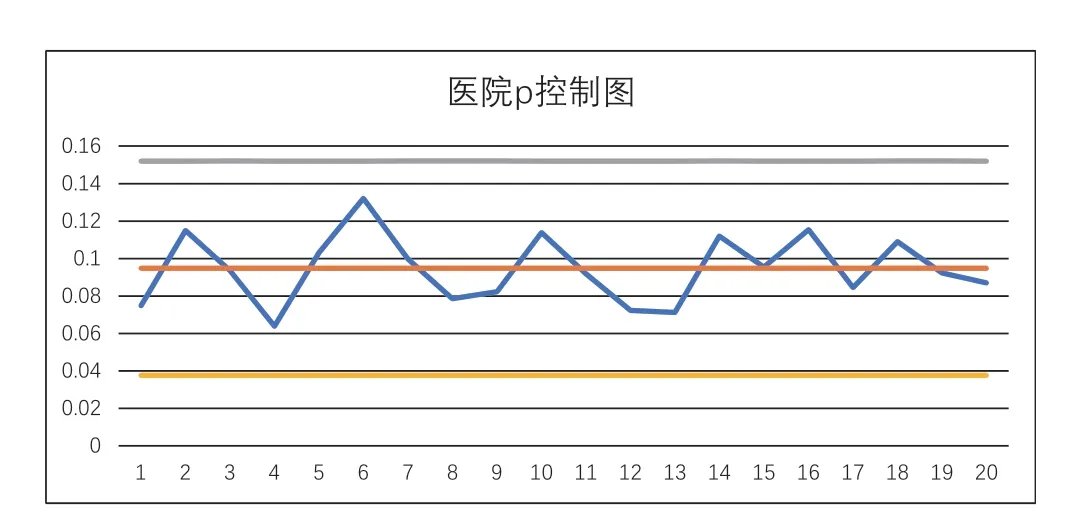
图4 医院p控制图（双普p控制图画法）

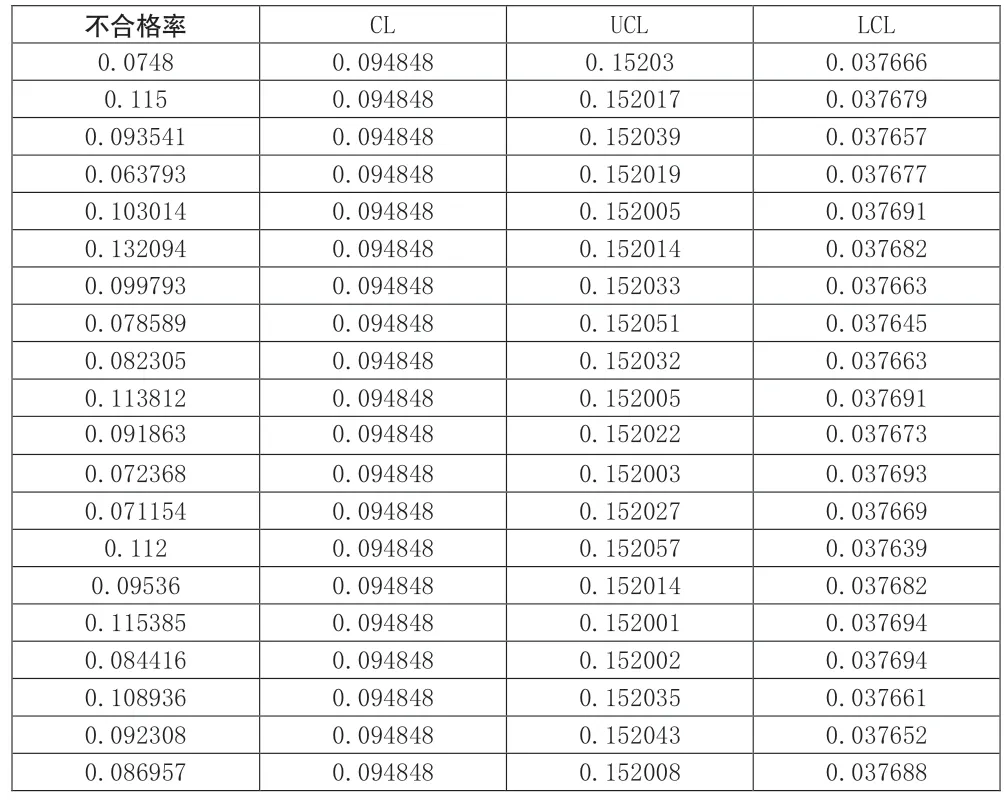
表5 画医院p控制图的数据界面

p图第四种画法[2]

根据文献[2]，美国聪明方案公司总裁福莱斯（Forrest Breyfogle）在美国《质量进展》杂志2003年和2004年10期上，发表了关于控制图的文章。福莱斯指出：“一个人可以把过程描绘成不受控的，但另一个人却可以把同一过程描绘成受控的。”福莱斯举了一个p图的例子，原来是不受控的，用p图的数据作成XmR图，就受到良好的控制了。

在美国的SPC文献里，类似作法绝非个案，可参见《上海统计》2000年第8期文章《应用控制图分析交通事故死亡人数的实例》。本文对“医院p控制图”也尝试使用该法，效果颇佳。XmR图也是休哈特控制图的一员，计算公式如下所示：

表6是XmR控制图的数据界面。左起第1列和第2列将相同数据叉开一格，是为了在第3列计算移动极差mR，它=“前1个数减后1个数取绝对值”。第3列最下的数是mRbar。第4列就是mR图的中心线。第5、6列是mR图的上、下控制限。选取左起3～6列，用Excel的折线图就得到mR图（见图5的上图）。

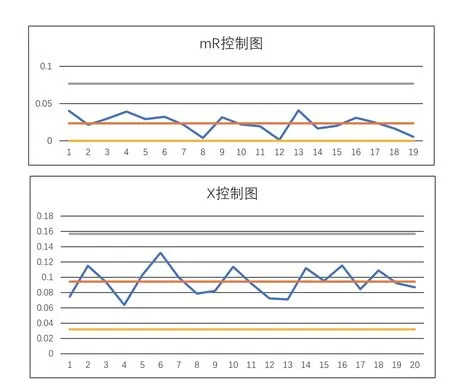
图5 医院p控制图（以XmR控制图画出）

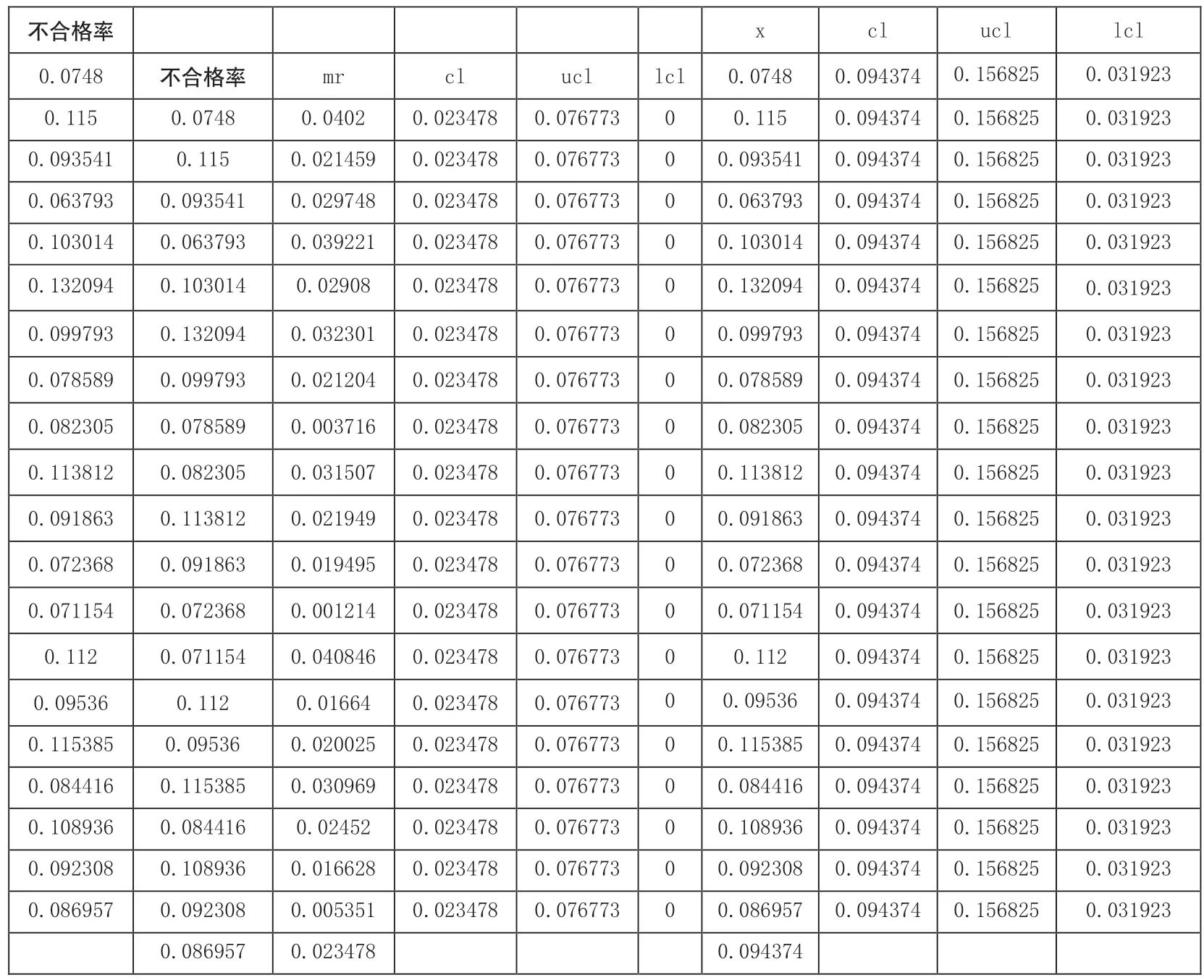
表6 医院p控制图（以XmR控制图画出）的数据界面

表6右边4列是画X控制图的。右4列最下的数是平均值，也就是右3列的值。右2、右1列是上、下控制限，根据公式（要用前面算得的mRbar）易得到。选取右4列，使用Excel折线图可得到X图（见图5的下图）。从数据和图形看，X控制图与“双普p控制图”很接近，但是前者显然更容易。