离心叶轮流场对背压脉动的响应特性研究*

肖 军 周逸伦 张宇航 刘晓明 李奉誉 孙永瑞 刘小民,*

（1.合肥通用机械研究院有限公司压缩机技术国家重点实验室；2.西安交通大学能源与动力工程学院；3.沈鼓集团股份有限公司）

0 引言

高转速离心压缩机在航空航天、石油化工、涡轮增压和燃料电池等领域有着广泛的应用。高转速离心压缩机的性能曲线十分陡峭，实际运行中极端非稳的边界条件使压缩机流动大尺度剧烈变化，流场的动态响应呈现高度复杂的非定常特性，开展不同背压的流场响应特性研究对保证高转速离心压缩机安全稳定运行具有重要的理论意义和实际应用价值。

关于高转速离心压缩机流场对边界条件变化的瞬态响应问题，目前的研究仍开展较少。早期的研究主要以轴流压缩机为对象，Wenzel[1]在某涡扇发动机进气道中反向喷入射流对进气压力进行脉冲降压，结果表明压缩机失速所需脉动幅度与脉冲持续时间成反比。吴虎等[2]对某四级跨音压缩机和八级跨音压缩机进气突变的计算研究表明，进气压力突增可延迟失稳，压力突降则增大失稳的可能性。王小峰[3]对某型发动机压气机的研究亦表明进气压力突降时，稳定工作边界下移，喘振可能性增大。近年来，已有学者开展了离心压缩机流场在非稳边界条件下的流场响应研究，如Zemp[4]对某离心压缩机进口施加实测的畸变分布边界条件，计算了进气畸变通过压缩机全场的非定常过程。肖军[5]开展了某径向叶轮流场对进口压力脉冲的响应特性研究。以高转速离心压缩机为对象的研究主要针对车用涡轮增压器压缩机在出口背压脉动下的响应特性展开[6-9]。Marelli[6-7]的研究表明，背压脉动条件下涡轮增压器离心压缩机的瞬态工作点偏离并包裹了定常工况性能曲线，试验发现压缩机性能迟滞回线的尺寸随着脉动频率的增加和压缩机转速的提高而增大，背压脉动条件下压缩机的喘振裕度得到改善。Galindo[8]的研究表明，背压脉动条件下离心压缩机的喘振流量降低了约15%。Barrera-Medrano[9]对一台涡轮增压器压缩机的试验亦表明，当压缩机在背压脉动条件下运行时，喘振边界被推至更小流量区间。Shu[10]通过某高速小流量离心压缩机的实验研究发现背压脉动对喘振频率影响很小，但在一定程度上削弱了喘振强度。然而上述研究均采用试验手段，侧重于对离心压缩机外特性的测试分析，目前少有通过计算流体力学手段开展背压脉动下流场响应机理的研究。

动态模态分解是近年发展起来的一种重要的数据降维方法，由Schimd[11-12]提出，可用于提取流场仿真和实验数据的模态特征，描述时间序列数据的演化过程及机制。已有较多学者采用DMD 方法对非定常流动过程展开了研究，如Liu 等[13]采用DMD 方法分析了某跨声速空腔湍流的压力波动过程，识别出不同频率的流场模态结构。李康迪等[14]采用DMD 方法对某跨声速压气机的流固耦合流场进行分析，得到了压力和速度的模态场，通过模态等值线图发现了近失速点突尖型失速的早期表现。张人会等[15]针对某轴流式油气混输泵导叶内的非定常流动采用DMD方法获得了反映速度场特征的前几阶模态场的信息，结果显示基于主要模态场的降阶重构能够较精确地实现时变流场的预测。Kou[16]提出了一种根据模态对时间系数的积分选择流场主模态的准则，该准则考虑了各模态在整个采样空间内的演化，并根据其对所有样本的贡献进行排序，使用该准则可用较少的模态准确重建时变系统的流场结构。本文研究的超高速离心压缩机背压脉动流场是高频时变流场，而目前流场的DMD 分析较少涉及高频时变流场特征的研究。

本文采用自主编写的离心叶轮流场数值分析程序，针对高速离心叶轮流场进行了不同背压脉动下的非定常响应计算及分析。然后采用DMD方法开展了不同背压脉动条件下流场响应的模态分析。结果表明：不同脉动频率下非定常流场均包含转频谐波的极限环振荡模态及非谐波的衰减模态。非定常流场可通过基本模态和前几个谐波模态进行较准确的重构，相较于基本模态，其它模态的幅值较小。不同背压脉动频率下一阶谐波模态的幅值均为除基本模态外最高，反映背压脉动诱发的非定常流场变化主要表现为基频响应。

1 数值方法

1.1 流场计算方法

基于多块结构化网格开发了非定常流场分析程序，主方程和湍流方程的离散方法以及非定常流场的时间推进方法参见文献[17-18]。使用多重网格方法加速流场计算，湍流输运方程仅在最细层网格求解。多核多线程并行计算是加速流场计算的最有效途径，本文数值计算采用基于共享内存的OpenMP 并行编译技术，在源代码中添加并行编译伪指令将程序执行并行化，最大限度地降低离心叶轮非定常流场模拟的计算时间。

针对离心压缩机叶轮，数值计算中叶轮进口边界设定总压、总温及湍流度边界条件，边界内侧格点的轴向速度外插，出口采用压力边界条件，给定平均背压，速度分量采用一维特征关系外插。固壁采用无滑移边界条件且给定法向压力梯度为零。

1.2 DMD方法

本文研究采用的动态模式分解（Dynamic Mode Decomposition，DMD）是一种有效的数据分解方法，允许从实验或仿真获得的时间序列数据中提取动态特征。对于非定常流场，各时间步的流场数据可表示为一个快照矢量，这些矢量的时间序列构成快照矩阵V1,n，即

式中，vi为第i个快照矢量，n为时间序列的步数，相邻快照时间间隔为Δt。DMD 方法通过计算近似快照间映射的低维矩阵的特征值和特征向量，生成描述时间序列中包含的流场动态过程信息。对于非线性的流体动力系统，假设相邻流场快照间存在近似线性映射A，使

A为m×m的高维矩阵，m为快照矢量空间维度，流体系统的动态特性包含于A的特征值和特征向量中。为获取流场的主要动态特性，必须对高维矩阵A进行降阶。当快照数量足够多时，快照矩阵产生线性相关组，即

表明进一步添加流场快照无法增加流场信息，此时可用A的伴随矩阵S作为其低维近似矩阵

对V1,n-1做QR 分解并根据上式可得到S最后一列，但该算法易导致病态矩阵[11]。

对时间序列V1,n-1进行奇异值分解得到

Σ为包含奇异值的对角矩阵，UTU=I且WTW=I，I为单位阵。通常前面几个奇异值的和即占全部奇异值和的99%以上，可对式(6)取前r阶非零奇异值做截断得到

流场动力系统的动态模态矩阵定义为

式中ω为的右特征矩阵，即

λi为的特征值。

上式表明b的物理意义为模态振幅，其算式为

由式(11)可知，特征值λi的虚部反映第i模态的频率fi，特征值的模反映该模态随时间的变化率ηi，具体地

θi为λi的相角，若变化率ηi为正，则相应模态发散，为负则衰减，为零表示极限环模态。

2 背压脉动的流场响应及其DMD分析

2.1 流场响应分析

高转速离心压缩机频繁经历着工况参数和边界条件变化，动态变化的工况导致离心压缩机内流场呈现复杂的响应特征。研究对象为某高转速小流量离心压缩机叶轮的内部流场，压缩机叶轮有8个主叶片和8个分流叶片，转速为90000r/min，模型如图1(a)所示，几何及气动设计参数如表1所示。

表1 离心压缩机设计参数Tab.1 Design parameters of centrifugal compressor

图1 压缩机叶轮及计算网格Fig.1 CAD model and computational grid of impeller

流场计算域包括进口延长段、叶轮通道、扩压器段，划分的多块结构化网格如图1(b)所示，网格点数为1,245,262。使用独立编制的数值计算程序展开了离心叶轮的流场数值模拟，无粘项离散采用迎风格式，粘性项离散使用中心格式，采用S-A湍流模型。首先进行叶轮定常流场的计算，设置进口总压101.3kPa、总温293.15K，叶轮下游背压pb=168.4kPa，该背压下工况接近设计流量点。

针对压缩机实际运行时下游压力可能发生的脉动变化，对叶轮下游背压施加一定幅度的周期波动，使用数值分析展开叶轮流场对背压脉动的响应研究。根据实测经验和前述文献[6-8]情况，实际多变工况下高速叶轮出口压力波动的幅度多在1%～5%的水平。对叶轮下游施加频率分别为叶轮转频（frot=1500Hz）、2 倍频和3 倍频的背压脉动，幅度为3%pb，上游进口总温、总压保持不变，以定常流场为初场，计算了叶轮在背压脉动条件下的响应流场。叶轮转频脉动情况下，每个脉动周期设置32个和128物理时间步得到的结果基本一致，因此各计算工况的脉动周期均设置32个时间步。

Fluent 软件与本文程序均采用二阶AUSM+格式离散对流项，实时间步离散均采用二阶欧拉后差格式，虚时间步离散均采用LU分解隐格式，进口均给定总温及总压，出口边界均给定静压，速度和密度由内场外插至出口边界，且两者均采用S-A 湍流模型。叶轮流场对背压脉动的进口质量流量和气动力矩响应分别如图2(a)、(b)所示，横坐标nT为背压脉动周期数。程序和商业软件计算得到的流量和气动力矩时域曲线符合较好，曲线变化的时域历程几乎一致，波峰和波谷时刻准确对应，比较结果验证了编制程序的正确性。该算例显示，在相同的网格和计算参数设置下，本文程序计算相同时间步数所需的CPU时间比软件降低约30%。时变曲线的结果表明，随背压脉动频率的增大，流场参数的波动幅度显著增加，流场变化愈加剧烈。

图2 性能参数时域变化曲线比较Fig.2 Comparison of time domian changes curves of performance parameters

图3、图5 和图7 分别给出了背压脉动频率为叶轮转频、2倍频和3倍频情况下两个时刻的相对速度场，t=T/4和t=T/4分别对应背压脉动最大值和最小值时刻。由图可见，不同脉动频率下的速度场在叶片前缘、叶片通道内及叶片尾缘均具有相似的等值线分布，且这种相似性在两个时刻的速度场之间同样存在，各速度场的相似性应来源于平均流场，而流场的非定常响应未根本改变平均流场的结构。可以看出两个背压极值时刻及不同脉动频率情况的速度场差异主要表现在相应区域色温的变化，3 倍频脉动情况下，叶片通道后部的速度场色温在t=T/4时刻最浅，在t=3T/4时刻最深，反映非定常流场响应的波动幅度最大，这与前述性能参数时变曲线反映的结果一致。图4、图6和图8分别给出了背压脉动频率为叶轮转频、2 倍频和3 倍频情况下最后一周期两个时刻的非定常压力，与速度场结果一样，各压力场分布呈现基本相似的结构，这里不再赘述。

图3 90%叶高位置非定常速度场(f=1500Hz)Fig.3 Unsteady velocity at 90%blade height(f=1500Hz)

图4 90%叶高位置非定常压力场(f=1500Hz)Fig.4 Unsteady pressure at 90%blade height(f=1500Hz)

图5 90%叶高位置非定常速度场(f=3000Hz)Fig.5 Unsteady velocity at 90%blade height(f=3000Hz)

图6 90%叶高位置非定常压力场(f=3000Hz)Fig.6 Unsteady pressure at 90%blade height(f=3000Hz)

图7 90%叶高位置非定常速度场(f=4500Hz)Fig.7 Unsteady velocity at 90%blade height(f=4500Hz)

图8 90%叶高位置非定常压力场(f=4500Hz)Fig.8 Unsteady pressure at 90%blade height(f=4500Hz)

2.2 非定常流场DMD分析

流场云图不能定量地描述背压脉动下非定常流场演化的动态特性，为此，本研究使用前述DMD方法对叶轮转频、2 倍频和3 倍频背压脉动情况下的叶轮非定常响应流场展开了动态特性分析。非定常流场计算完成后，取90%叶展位置4 个脉动周期的速度场及压力场数据，共130 个流场快照进行DMD分析。图10所示为各脉动频率下流场响应的模态特征值分布情况，虚部非零的模态为成对出现的共轭模态，红点表示频率为转频倍数的前几阶谐波模态特征值，数字表示谐波阶数。显见特征值均位于单位圆圆上或圆内，其中谐波模态的特征值均位于单位圆边界上，反映谐波模态对应的非定常流场响应均表现为极限环振荡，非谐波模态特征值位于单位圆内，对应流场响应表现为随时间衰减的耗散态势。在背压基频脉动情况下，约半数模态为非谐波耗散模态，随脉动频率的增大，特征值越来越集中于单位圆边界附近，即趋于极限环振荡的模态数显著增加，3 倍频背压脉动情况下，仅有1/4 的模态位于单位圆内部，3/4的模态聚集在单位圆边界附近，反映背压脉动诱发了更多非谐波成分的稳定流场响应结构。

图10 模态场特征值分布Fig.10 Eigenvalues distribution of flowfield modes

图11 所示为各模态的幅值，横轴为模态频率与转频比，红点及数字标记前几阶谐波模态，显见零阶模态的幅值相同且远大于其它模态，零阶模态为频率为0的基本模态，反映了非定常流场响应的某种平均流场。不同脉动频率下一阶谐波模态的幅值均远高于二阶和三阶谐波模态，非谐波模态的幅值远低于谐波模态，该结果表明无论背压脉动频率怎样变化，流场的非定常响应主要受一阶谐波模态支配。随背压脉动频率的增大，各频率模态的幅值均显著增大。流场模态的上述特性已由2.1节的非定常流场结果所体现，即流场结构的相似性来源于基本模态表达的平均流场，3 倍频脉动时流场响应的波动幅度增大因各模态幅值增大所致。此外，由各模态幅值可知，流场响应可由基本模态和前几阶谐波模态近似描述。

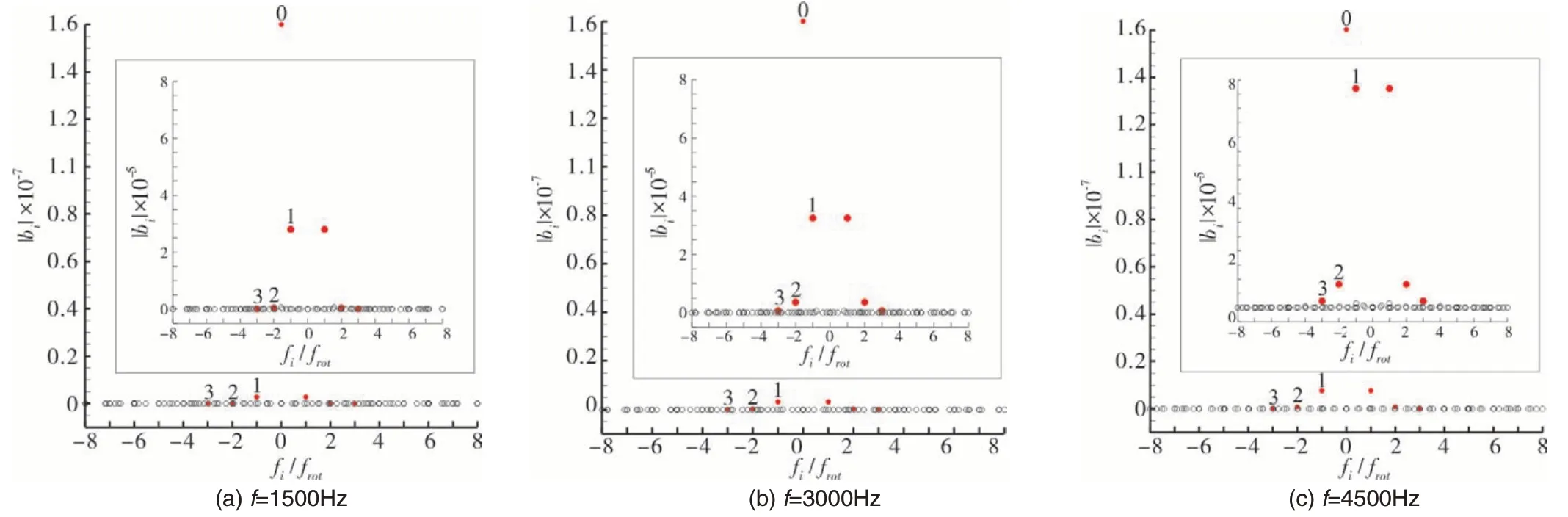
图11 不同频率下的各阶模态幅值Fig.11 Amplitudes of modes at different frequencies

图12 所示为背压脉动下非定常流场响应的基本模态场，结果表明不同脉动频率下流场快照数据提取的速度场基本模态比较一致，并未因背压脉动频率不同而变化，根据前述模态特征值中基本模态的幅值相同且远高于其它模态的结果，进一步表明图3、图5 和图7 中速度场的相似性即源于基本模态场，这也反映了平均流场的结构。不同背压脉动频率下流场响应提取的压力场基本模态亦比较一致，因此文中仅给出3倍频脉动下流场压力的基本模态。

图12 基本模态场Fig.12 Basic mode of transient flow field

图13、图15 和图17 所示分别为背压基频、2 倍频和3倍频脉动情况下流场非定常压力的前两阶谐波模态，谐波模态反映了非定常压力波动的分布特征，由图可见基频脉动情况下压力波动在叶轮进口前及出口后区域数值较低而在叶片通道内为负，2 倍频和3 倍频脉动情况下叶轮通道前部和中部分别出现较高正向压力波动，向上下游压力波动变为负向，反映流场局部涡系对压力变化造成的影响。二阶谐波模态压力波动数值较小，且分布相对一阶谐波模态较均匀。

图13 压力场模态(f=1500Hz)Fig.13 Pressure field modes(f=1500Hz)

图14 非定常压力场重构(f=1500Hz)Fig.14 Reconstruction of unsteady pressure field(f=1500Hz)

图15 压力场模态(f=3000Hz)Fig.15 Pressure field modes(f=3000Hz)

图16 非定常压力场重构(f=3000Hz)Fig.16 Reconstruction of unsteady pressure field(f=3000Hz)

图17 压力场模态(f=4500Hz)Fig.17 Pressure field modes(f=4500Hz)

略去其它模态，仅提取动态压力的基本模态和前3阶谐波模态对仿真计算最后一个周期的流场数据进行时序重构，得到图14、图16和图18所示的背压基频、2倍频和3倍频脉动情况下非定常压力的时序重构结果，分别与图4、图6 和图8 中的流场仿真结果相比，可知重构的压力场与数值仿真结果高度一致，几乎反映了原始流场快照的所有细节，这表明运用DMD 分解的流场模态数据能够准确重构时变流场的结构。对于叶轮流场这类周期变化的流场结构，随着耗散模态随时间的充分衰减，非定常流场将完全呈现谐波模态极限环振荡的变化态势，利用已有的仿真数据做DMD分解的模态场可实现对任意周期时刻流场数据的准确预测。

图18 非定常压力场重构(f=4500Hz)Fig.18 Reconstruction of unsteady pressure field(f=4500Hz)

3 结论

本文针对高速离心压缩机叶轮内部流场，对背压脉动情况下离心叶轮的非定常流场响应特性进行了数值分析，采用DMD分解方法对离心叶轮非定常流场的动态特征进了研究。得到的主要结论如下：

1）背压脉动频率对离心叶轮非定常流场响应有重要影响，随脉动频率增大，叶轮流量和气动力矩等流场参数的波动幅度显著增加，叶轮内流场变化愈加激烈。

2）不同背压脉动频率和演化时刻的离心叶轮流场分布呈现一定相似性，这种相似性主要来源于基本模态描述的平均流场。

3）离心叶轮非定常流场响应的模态包含转频谐波的极限环振荡模态和随时间衰减的非谐波模态，基本模态的幅值远高于其它模态，谐波模态幅值随阶数增加而迅速降低，非谐波耗散模态的幅值远低于谐波模态。叶轮内流场响应的非定常成分主要受一阶谐波模态支配。

4）不同背压脉动频率下离心叶轮流场提取的基本模态场一致，这表明叶轮内非定常流场响应的平均流场结构具有相似性。通过基本模态和前几阶谐波模态能够对非定常变化的叶轮流场进行准确的时序重构，本文研究采用较小的数据量揭示了离心叶轮内原始时变流场的演化特性。

本文对高转速离心叶轮内非定常流场演化的动态特征采用DMD 方法进行快速辨识，在无需额外流场数值模拟的情况下，实现了复杂时变流场的降阶重构和预测，对于深刻认识高速离心压缩机叶轮内非定常流场演化机理具有十分重要的理论意义。