微孔陶瓷管道渗灌土壤水分分布特性研究与关键技术参数优化
张甲森,刘旭飞,张春华,张 林
(1.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100;2.西北农林科技大学水土保持研究所,陕西 杨凌 712100)
0 引 言
渗灌是将具有无数微小孔隙的地下多孔渗水管埋入表层土壤以下一定深度处并将灌溉水缓慢渗入到作物根区土壤的地下节水灌溉技术[1],通过将多孔渗水管埋于作物根系土壤,直接向作物根系连续低流量灌溉,可为根系层土壤营造适宜稳定的土壤水分环境[2,3],并基于多孔渗水管的渗灌系统可在水流自身重力和土壤毛细管作用力影响,将水分扩散到表层土壤以下,可有效降低水分蒸发损失,抑制杂草生长,提高水分利用效率[4]。渗灌作为先进的地下节水灌溉技术,对于现代农业生产发展具有十分重要的意义。
塑料渗灌产品大多由不可降解的化学原料制备,在田间应用过程中若回收处理不当,会造成微塑料污染,严重时会造成土壤中有毒物质积累,并最终危害国家粮食和人民生命健康安全。农田土壤中的微塑料会显著破坏土壤细菌群落的多样性和生态结构,对土壤理化性质、土壤动植物生长等均产生不利影响,损害土壤健康[5-7]。因此,微孔陶瓷渗灌作为节水、节能的新型地下灌溉方式,通过将微孔陶瓷灌水器或管道埋置于地下,进行微压或零压灌溉,可持续性地为农田灌溉提供帮助,缓解环境负担[8]。
近年来,大量学者利用微孔陶瓷渗灌开展了田间研究,陶瓷灌水器的主要原料为天然黏土或石英砂,不仅对土壤环境更为友好,而且会极大简化当灌溉系统超过使用年限时的后处理步骤,在生菜、番茄、菠菜、枸杞、苹果等作物上表现出了显著节水增产效果[2,9-12]。但目前利用人工拉坯法和机械挤压法制备的多孔陶瓷渗灌管,存在着坯体壁厚难以掌握,坯体变形程度大等缺点[13,14]。因此,将绿色环保、适用性强、成型技术易掌握的注浆成型法引入到多孔陶瓷渗灌管道研发中,可能成为提高陶瓷渗灌管材料和水力性能,保证渗灌系统安全稳定高效运行的重要新思路,在生态环境和农业灌溉领域具有广阔发展前景。
目前,研究土壤水分入渗过程是评估渗灌管道水力性能的重要方式,土壤水分入渗以管道内外水势差为主要驱动力[15],基质势和压力势是影响微孔陶瓷渗灌管道水分入渗的主要因素。现有的渗灌试验研究大多从湿润锋运移情况、土壤含水量变化、累计入渗量和灌水器出流量角度分析土壤水分运移规律,Wei等[16]利用土箱试验深入研究了低压塑料渗灌管的土壤水分运动规律并以最优根水匹配度优化了渗灌管的工作水头和埋深;陈高听[17]通过HYDRUS-2D 模型对土壤水分入渗规律进行动态模拟,研究了不同工作压力下的土壤水分运动规律,但研究对象均为塑料渗灌管。Liu 等[9]试验表明利用微孔陶瓷灌水器调节土壤含水率,通过负压自动控制的方法满足作物生长温湿度需求,对加快作物生长和提高作物产量有显著影响,但其研究也尚未对管道周围土壤水分时空变化进行系统性研究。Vaghei 等[18]在干旱半干旱地区采用多孔陶瓷材料管道,研究了10~100 kPa 静水压力下管道流量和土壤水分分布情况,仅得出土壤湿润体形状呈垂直椭球形,并未对渗灌管道湿润锋运移进行深入研究。由此可见,目前大多研究并未采用土箱试验深入研究微孔陶瓷渗灌管道在土壤水分入渗过程水分空间分布特征,其土壤水分入渗特性尚未明晰。
为此,本研究采用注浆成型法制备微孔陶瓷渗灌管道,通过土箱试验和数值模拟相结合的方法,研究不同工作水头条件下微孔陶瓷渗灌管道土壤水分运移规律。在此基础上,结合3种典型作物根系分布规律,以最优根水匹配度为优化目标,对微孔陶瓷渗灌管道工作水头进行优化,研究结果可为微孔陶瓷渗灌管道的推广应用提供重要理论依据。
1 材料与方法
1.1 试验材料
本研究主要以微孔陶瓷渗灌管道为研究对象,该渗灌管采用注浆成型法制备,主要原料为黏土、炉渣、水和硅酸钠。黏土为陶瓷渗灌管的骨架材料,炉渣为造孔剂、水为黏结剂、硅酸钠为解凝剂。取陕西杨凌耕作土壤(0.05~0.45 m),将取得土壤经粉碎机粉碎10 min后,过50目(孔径0.355 mm)筛,得到粒径范围为0.18~0.355 mm 的黏土原料。炉渣取自当地陕西渭河某发电厂,其主要的化学成分是SiO2、Al2O3等氧化物,为粒径5~20 mm 的灰黑色固体颗粒。硅酸钠购自陕西咸阳某化工企业,在陶瓷坯体制备过程中掺入少量(质量比约0.1%)即可改善浆料流动性,保持黏度适中避免出现缩釉等现象,防止浆料絮凝。将上述黏土和炉渣按照4∶1 的质量比充分混合,再置于搅拌机中低速搅拌均匀,搅拌30 min 后,按照固体材料:水=66∶34 的质量比,将水放入搅拌机中搅拌30 min,再加入0.1%的解凝剂,得到浆料。而后,将浆料注入石膏模具中,使其形成圆管状湿坯,再将湿坯置于105 ℃的烘干箱内烘干90 min,再放入高温电窑以1 085 ℃高温烧结2 h,最终得到渗灌管道成品。注浆成型法制备而得的微孔陶瓷渗灌管道材料性能优良,收缩率、抗弯强度、抗拉强度和抗剪强度分别为4.67%、16.9 MPa、13.4 MPa和8.7 MPa,且此类微孔陶瓷能较好地满足田间应用要求[19]。
马氏瓶整体高度1.25 m,安置于0.5 m 的试验台上提供恒定水头;毛管采用管径2 cm 的PE 管,连接马氏瓶与微孔陶瓷渗灌管道;有机玻璃土箱主要材质为聚甲基丙烯酸甲酯,规格为100 cm×100 cm×90 cm(长×宽×高),土箱四周透明且能够较为明显地观察到土壤水分运动情况;本试验采用的黏壤土来自于杨凌区及附近的试验大田,于土壤表层0~15 cm 处选取土样,土样经自然晾干后,过筛去除根系等杂质分层填入土箱,每填入5 cm 试验土样后压实,保证每层试验土样密实度均匀,填土高度为80 cm,试验土样物理特性如表1 所示。微孔陶瓷渗灌管道总长度为100 cm,管道埋深为30 cm,距土箱底部50 cm,于土箱中水平铺设,管道中心距土箱左右两侧50 cm,管道布置见图1。
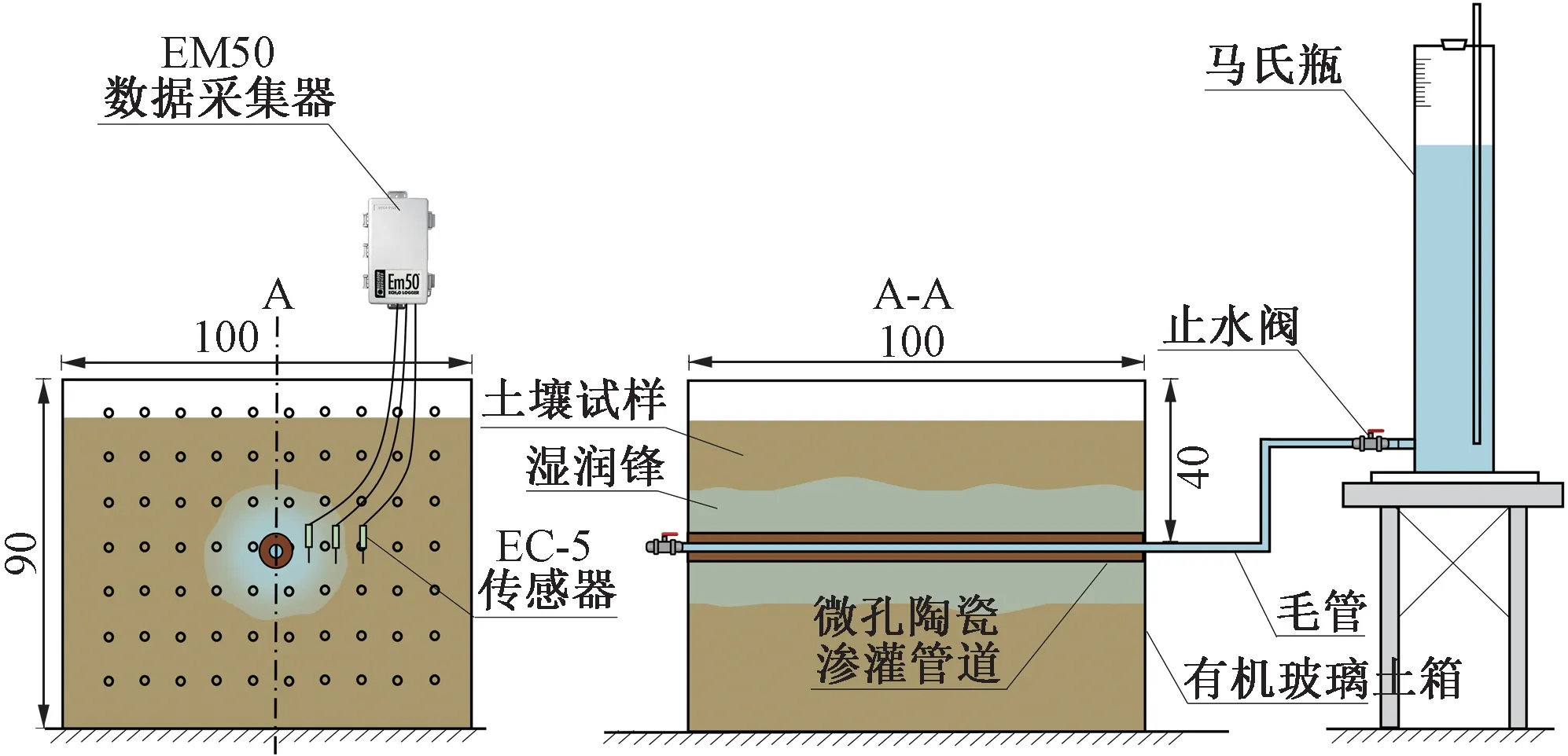
图1 微孔陶瓷渗灌管道土壤入渗试验示意图(单位:cm)Fig.1 Microporous ceramic infiltration pipe soil infiltration test

表1 土壤物理特性Tab.1 Physical properties of the soil
1.2 试验设计
为研究微孔陶瓷渗灌管道土壤入渗过程,本研究在陕西省杨凌区现代农业创新园(108°02′E,34°18′N)的内进行土箱入渗试验。试验装置如图1 所示,主要由马氏瓶、止水阀、毛管、有机玻璃土箱、供试土壤、微孔陶瓷渗灌管道和土壤水分采集系统组成(图1)。微孔陶瓷渗灌管道单宽流量及累计入渗量通过记录相应时间内马氏瓶内液面高度差推算[20]。通过观察记录有机玻璃土箱外壁湿润区域以测量水平、垂直向上和垂直向下湿润锋[21]。土壤含水量利用EM50 系列数据采集器(ECH2O 土壤含水量监测系统核心部件)进行监测,在距土壤表面30 cm处安装3个ECH2O土壤水分传感器探针,各传感器相距6 cm,监测时间间隔为5 min,传感器埋设位置为30 cm 土层深度,待土壤湿润区域不再变化时结束试验,试验时间48 h。此外,土箱入渗试验共设置3 组,分别为0.25 m、0.5 m、0.75 m,每组入渗时间均为48 h,该试验每组同时进行3组重复。
1.3 土壤水分入渗模型
1.3.1 渗透系数
利用马氏瓶提供的不同工作压力调节工作水头,制得的陶瓷渗灌管道流量额定流量为0.068 2 L/(h·m)(0.2 m 工作水头),并且流量随工作水头的增加而增大(图2)。采用达西定律可描述不同工作压力水头下微孔陶瓷渗灌管道流量:
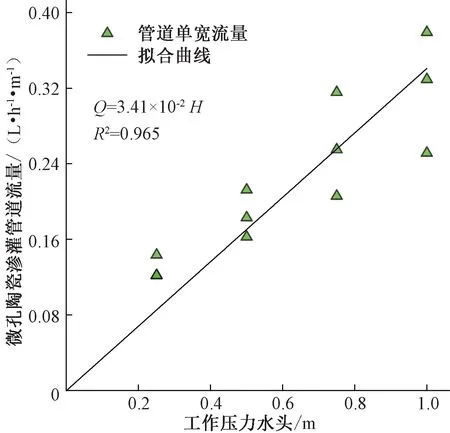
图2 不同工作水头下微孔陶瓷渗灌管道流量Fig.2 The flow rate of microporous ceramic infiltration pipe under different working heads
式中:Q为管道单位宽度流量,cm3/(h·cm);Ks为水力传导系数,cm/h;H为提供的工作压力水头,m;δ为微孔陶瓷渗灌管道的厚度,cm,δ=1 cm;d为微孔陶瓷渗灌管道的直径,cm,d=2 cm。工作压力水头和管道单宽流量之间的线性函数关系如图2 所示,管道流量与工作压力水头函数关系式见式(2)。
在空气中进行微孔陶瓷渗灌管道出流试验,微孔陶瓷渗灌管道流量和工作压力水头呈正相关,因此结合公式(1)、(2) 可得出微孔陶瓷渗灌管道水力传导系数Ks=5.5 × 10-3cm/h。
1.3.2 土壤水分入渗规律数学模型
本试验利用HYDRUS-2D模拟软件,模拟了水从微孔陶瓷渗灌管道向供试土壤渗透过程。三组试验均将微孔陶瓷渗灌管道看作半圆柱形恒定水头水源,将管道内水分入渗过程假设为轴对称,由于供试土壤密实度均匀,进而整个土壤水分入渗过程可以用Richards方程[25]来描述:
式中:θ为土壤体积含水量,cm3/cm3;z和r分别为径向和垂直空间坐标;K(h)为非饱和土壤导水率,cm/min;t为时间,min。
本试验模拟的是恒定水头下微孔陶瓷渗灌管道的土壤水分入渗规律,土壤体积含水量和非饱和土壤导水率可以用van Genuchten模型[22]的常规表达式描述:
式中:θs为土壤饱和含水量,cm3/cm3;θr为土壤残余含水量,cm3/cm3;α为经验参数,1/cm;h为土壤负压水势,cm;Ks为渗透系数,cm/min;Se为土壤有效含水量,cm3/cm3;m和n分别是拟合参数,m= 1 - 1/n,n> 1。土壤水力特性参数见表2。

表2 土壤水力特性Tab.2 Hydraulic properties of soil
1.3.3 系统边界与初始条件
大多数间作系统中作物根系在竖直方向上主要分布范围为0~80 cm 深度[23],为研究灌溉过程中的深层渗漏,因此,土壤水分入渗模拟中使用深度为80 cm 的土壤剖面,模拟区域为50 cm × 80 cm 的矩形,其中最上层为大气边界,宽度为50 cm,最底层为深层渗漏边界,微孔陶瓷渗灌管道管径2 cm,厚度1 cm,提供恒定水头作为恒定水头边界,由于左右两侧对称,本研究只模拟右侧土壤剖面土壤水分运移。HYDRUS-2D 模拟中网状几何和边界条件如图3 所示。本试验土箱内的供试土样初始含水量均为0.12 cm3/cm3,运用式(4)将含水量转换为负压水头,公式中参数值如表2所示,计算得到微孔陶瓷渗灌管道恒定水头边界处负压水头为-8 638.83 cm。
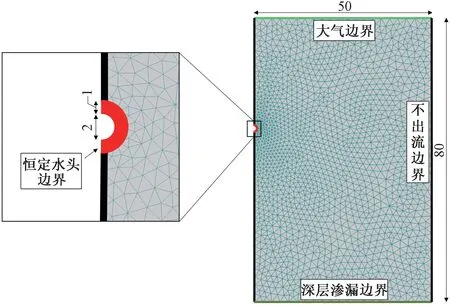
图3 网状几何和边界条件(单位:cm)Fig.3 Mesh geometry and boundary conditions
1.3.4 模型评价
本模型利用平均绝对值误差(MAE)、均方根误差(RMSE)和决定系数R2评估HYDRUS-2D 模型预测水平与实测数据的一致性[24]。
2 结果
2.1 微孔陶瓷渗灌管道出流特性
图4为微孔陶瓷渗灌管道实测和模拟湿润锋、累计入渗量和土壤含水量关系。从图4 中可以看出,数据点接近于1∶1线,MAE和RMSE分别小于0.8 和0.9,R2大于0.75,这说明所构建的HYDURS-2D模型能以较高精度反映微孔陶瓷渗灌管的湿润锋、累计入渗量和土壤含水量。
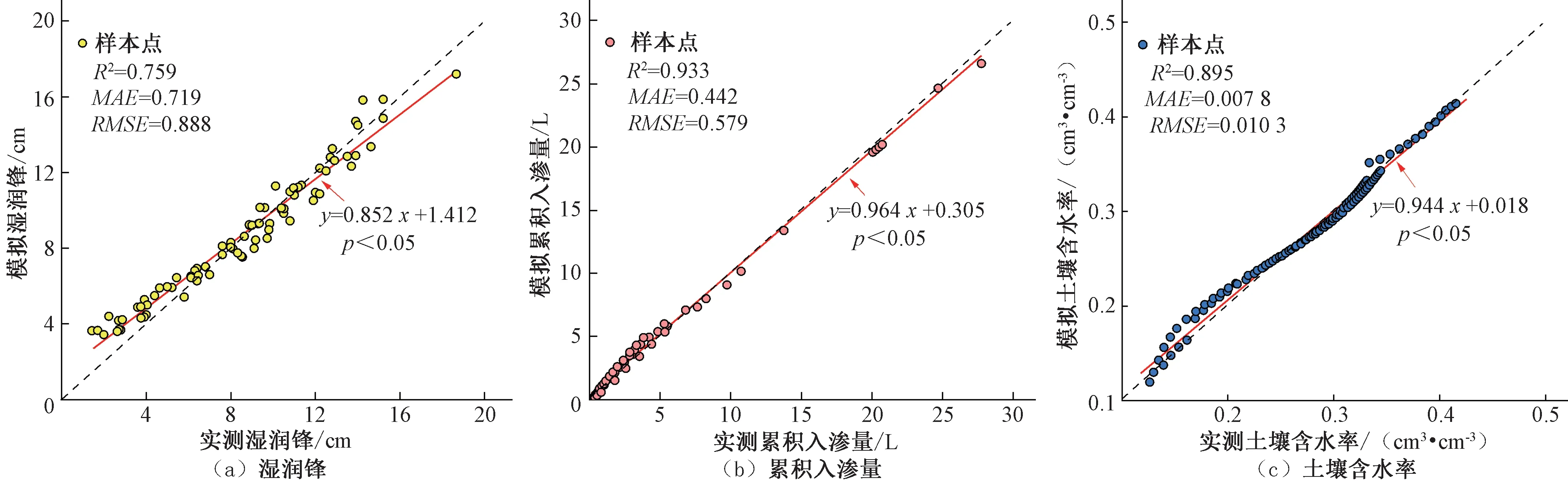
图4 实测和模拟湿润锋、累计入渗量、土壤含水量间数学关系Fig.4 The mathematical relationships between measured and simulated wetting front, cumulative infiltration and soil water content
图5(a)为不同工作水头下微孔陶瓷渗灌管道流量随时间的变化。由于微孔陶瓷渗灌管道周围土壤快速接近饱和,渗灌管道周围土壤含水量对渗灌管道流量具有反馈调节作用,导致流量下降[26],从图5中可以看出,微孔陶瓷渗灌管道流量在1 h 内迅速下降,于48 h 后达到稳定出流状态,并以相对稳定的流量持续出流(此处称为稳定出流量)。例如,当工作压力为0.50 m 时,微孔陶瓷渗灌管道流量先在1 h 内从初始的2.164 L/(h·m)降低为初始值的10.76%,然后在1-36 h内流量小幅度下降,最终于48 h后微孔陶瓷渗灌管道保持0.212 L/(h·m)的稳定出流量持续稳定出流,这说明微孔陶瓷渗灌管道可以在作物生育期内以极低的流量进行连续灌溉。此外,微孔陶瓷渗灌管道稳定出流量随工作水头的增大而增大,当工作水头从0.25 m 增加至0.75 m 时,微孔陶瓷渗灌管道稳定出流量由0.157 L/(h·m)增加至0.270 L/(h·m),增加了71.97%。

图5 不同工作水头下微孔陶瓷渗灌管道流量与时间的关系、不同工作水头与渗灌管道稳定流量的关系Fig.5 The relationship between flow rate and time of microporous ceramic infiltration pipe under different working heads、Relationship between different working heads and stable outflow rate of microporous ceramic infiltration pipe
通过HYDRUS-2D数值模拟的方法,进一步地绘制了如图5(b)所示的不同工作水头下微孔陶瓷渗灌管道在稳定出流状态的流量变化情况。由图5(b)可知,微孔陶瓷渗灌管道在0.05 ~0.75 m 工作水头的微压条件下,由于渗灌管道流量变化是渗灌管道外基质势和压力势作用所致,且渗灌管道在稳定出流阶段其周围的土壤水势为定值,则微孔陶瓷渗灌管道稳定出流量与工作水头呈显著的线性正相关关系[19,27]。当工作水头从0.05 m 增加至0.75 m 时,微孔陶瓷稳定出流量由0.157 L/(h·m)增加至0.270 L/(h·m)。这说明在实际应用条件下,微孔陶瓷渗灌管道可通过改变工作压力调节稳定出流量,以适应不同生育期作物的灌溉需水量要求,实现主动灌溉。
2.2 土壤水分的时空变化
由于微孔陶瓷渗灌管道在土箱中入渗形成的湿润体剖面为近似于左右对称的圆形,故在此仅展示1/2 湿润锋说明运移情况。图6为不同工作水头下入渗48 h内微孔陶瓷渗灌管道土壤水分分布图。从图6中可以看出,微孔陶瓷渗灌管道附近土壤含水量较高,接近达到土壤饱和含水量,并沿湿润锋运移方向土壤含水量逐渐降低。当入渗时间为48 h 时,工作水头为0.25 m 的微孔陶瓷渗灌管道水平、垂直向上和垂直向下的湿润锋运移距离分别为0.253 7 m、0.250 9 m 和0.258 9 m,湿润面积为0.203 4 m2,并且湿润面积随入渗时间的延续小幅度增大。此外,入渗初期,土壤水分入渗的主要驱动力为土壤吸力,水势差受工作压力影响较小[28],当入渗48 h,工作水头由0.25 m 增加至0.75 m 时,稳定出流状态的湿润面积从0.203 4 m2增加至0.345 6 m2,增幅为69.91%。如图6 所示,当入渗时间为48 h 时,湿润体内平均土壤含水量也随工作水头的增加而增大,平均土壤含水量从0.25 m的0.243 cm3/cm3增加至0.75 m 的0.406 cm3/cm3,增幅为67.07%。这说明通过调节工作水头,可以控制微孔陶瓷渗灌管道土壤水分入渗过程,以实现最优水分供给。

图6 模拟3种工作水头下48 h后的微孔陶瓷渗灌管道湿润锋图Fig.6 The wetting front of microporous ceramic infiltration pipe after 48 h under three working heads was simulated
为精确描述不同工作水头下微孔陶瓷渗灌管道土壤水分入渗过程,绘制了如图7所示的垂直向上、垂直向下和水平湿润锋运移距离以及湿润体内平均土壤含水量随时间的变化规律。从图7(a)~图7(c)可以看出,在入渗初期,随着土壤入渗时间增加,垂直向上、垂直向下和水平湿润锋运移距离逐渐增加,但随着时间延长,湿润锋在入渗后期运移距离差值逐渐减小,湿润锋各方向运移距离变化率与时间呈负相关,湿润面积变化越来越小,而后基本维持不变[8,29]。此外,垂直向上、垂直向下和水平湿润锋运移距离随工作水头的增加而增加。以入渗时间48 h 为例,当工作水头由0.25 m 增加至0.75 m 时,垂直向上湿润锋运移距离从25.09 cm 增加至28.6 cm,垂直向下湿润锋运移距离从25.89 cm 增加至29.1 cm,水平湿润锋运移距离从25.37 cm 增加至28.67 cm。以0.75 m 工作水头为例,在入渗后期即第48 h 时,垂直向上、垂直向下和水平方向的湿润锋分别以0.05 cm/h、0.08 cm/h 和0.04 cm/h 的速率扩散,湿润面积基本维持稳定。由于土壤水分受重力作用,垂直向下湿润锋运移距离仅比垂直向上湿润锋运移距离和水平湿润锋运移距离多0.5 cm和0.43 cm。
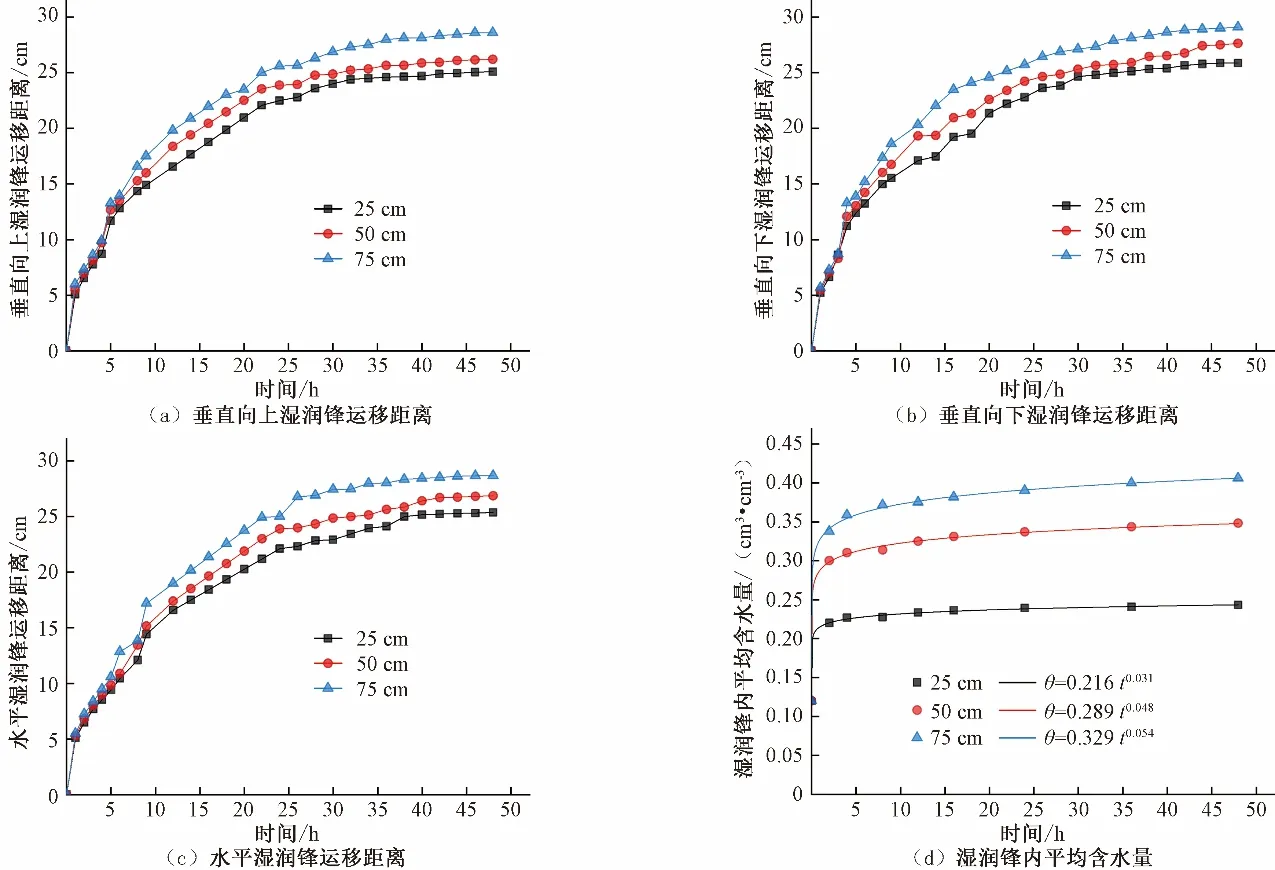
图7 微孔陶瓷渗灌管道湿润锋与湿润体平均土壤含水量随时间变化规律Fig.7 The microporous ceramic infiltration pipe wetting front and average soil water content of the wetting body of the changes with time
由图7(d)可知,湿润体内平均土壤含水量在1 h内迅速上升,入渗48 h 后,湿润体内平均土壤含水量保持在稳定状态。例如,当工作压力为0.25 m 时,湿润体内平均土壤含水量先在1 h 内由初始土壤含水量0.120 cm3/cm3迅速增长至0.238 cm3/cm3,然后随着入渗时间增加,当达到稳定出流状态,湿润体内平均土壤含水量保持在0.243 cm3/cm3。此外,湿润体内平均土壤含水量随工作水头增加而增加,入渗48 h后, 0.25 m、0.50 m和0.75 m工作水头下湿润体内平均含水量分别为0.243 cm3/cm3、0.348 cm3/cm3和0.406 cm3/cm3。
2.3 微孔陶瓷渗灌管道工作水头确定
根据HYDRUS-2D 模型模拟结果,表3 给出了入渗48 h 后微孔陶瓷渗灌管道稳定出流量、水平、垂直向上、垂直向下湿润锋运移距离以及湿润体内平均土壤含水量与工作水头间的数学关系。为确定微孔陶瓷渗灌管道最优工作水头,以根水匹配度最高为优化指标,建立目标函数:

表3 入渗48 h后土壤水分入渗参数与工作水头间的数学关系Tab.3 The mathematical relationship between soil water infiltration parameters and working heads after infiltration for 48 h
式中:q为微孔陶瓷渗灌管道稳定出流量,L/(h·m);I为灌水量,mm;S为种植面积,hm2;N为株数,棵;D为灌溉天数;X为水平湿润锋运移距离,cm;Z+为垂直向上湿润锋运移距离,cm;Z-为垂直向下湿润锋运移距离,cm;Lz为根系深度,cm;Lx为根系深度,cm。
约束条件:
通过上述目标函数,结合不同作物需水量及根系空间分布情况,进而根据土壤水分入渗参数,获得微孔陶瓷渗灌管道最优工作水头。表4给出了在与试验土样物理特性相似的试验条件下常见的冬小麦、玉米和番茄3种根系分布特征密植作物的微孔陶瓷渗灌管道适宜工作水头。表4中不同密植作物的适宜灌水量、生育期时间、根系深度和宽度可见参考文献。

表4 典型密植型作物的工作水头优化Tab.4 Working head optimization of typical close planting crops
3 讨 论
由于微孔陶瓷渗灌管道依靠其内部相互连通的微米级孔隙出流,其入渗过程可理解为多孔介质出流,因此影响渗灌管道流量变化的主要因素是工作水头与外部土壤水势[33]。蔡耀辉等[34]通过分析微孔陶瓷灌水器出流过程中的力能关系,发现当土壤干燥时灌水器同时受到工作水压和土壤水吸力的共同作用,并随土壤含水量的增加,土壤水吸力逐渐降低,最终表现为灌水器出流量随入渗时间的延续逐渐降低。本研究中微孔陶瓷渗灌管道出流量也呈现相同的变化趋势,这说明陶瓷灌水器结构形式并不改变其内部出流机理。然而,Liu 等[9]利用微孔陶瓷灌水器进行温室番茄灌溉,发现作物生育期内微孔陶瓷灌水器出流量连续随机波动,而本试验中微孔陶瓷渗灌管道出流量基本维持稳定,这可能是土箱试验条件下土壤水分环境相对稳定所导致的。近年来,Cai 等[35]运用HYDRUS-2D 数值模拟软件预测了微孔陶瓷灌水器在不同运行管理参数条件下流量变化规律,并利用灌水器稳定出流量对微孔陶瓷灌水器工作水头进行了优化,这说明本研究中以最优根水匹配进行渗灌管道工作水头优化是可行的。
王辰元[36]与欧阳淼[37]在地下滴灌土壤水分入渗试验中发现了相似结果,然而地下滴灌灌水器所形成的土壤湿润体近似于椭圆,且垂向湿润距离显著大于水平湿润距离,这主要是工作水头较高、滴头流量较大所导致的。微孔陶瓷渗灌与地下滴灌的土壤水分运移规律和机理不同,在灌溉过程中,微孔陶瓷渗灌在低压条件下依靠土壤基质势动态调节,湿润体内土壤含水量变化较小,提供了恒定的水分环境,地下滴灌虽然可以采取干湿交替的被动恒压灌溉方式[8],但土壤含水量不易控制,且操作复杂。低压微孔陶瓷渗灌管道入渗过程主要受管道内外水势差影响,入渗后期由于渗灌管道周围土壤接近饱和[8],当微孔陶瓷渗灌管道入渗48 h后,其土壤入渗基本维持稳定,此时土壤基质势较低,微孔陶瓷渗灌管道稳定出流量受工作压力影响较为明显,这一现象与牛文全研究结果吻合[27],因此可根据作物的需水量,通过调节工作水头实现实时补水的主动灌溉。而微压灌溉条件下的湿润锋尚未接触到深层渗漏边界,垂直向下运移的水分深度未能达到深层渗漏条件,这说明渗灌管道在控制土壤湿润区域和降低土壤水分深层渗漏方面可能存在明显优势,Liu 等[9]也发现了相似现象。与传统微孔陶瓷灌水器相比,由于微孔陶瓷渗灌管道需考虑边界问题,所形成的湿润体为平行于土壤表面的圆柱体,故将其作为柱状面源入渗进行分析[8,38],因此在实际应用中,为充分利用微孔陶瓷渗灌的入渗特点与提供稳定土壤水分环境的优点,可将研究所提出的渗灌管道应用于密植型作物。
进一步地,本研究以最优根水匹配为优化目标,对冬小麦、玉米和番茄3种典型密植型作物的微孔陶瓷渗灌管道工作水头进行了优化,发现番茄适宜工作水头最高,而冬小麦作物工作水头最低(表4),工作水头优化结果是可以预见的,这是因为与玉米和冬小麦相比,番茄作为一种典型密植型经济作物,由于根系发达且吸水能力强,对土壤水分敏感,因此需要更高的灌溉水量以保证产量[32],而根据过往研究发现,张子卓[39]认为利用微润带灌溉番茄适宜的工作水头为120~200 cm,蔡耀辉[19]研究发现微孔陶瓷灌水器无压或微压灌溉番茄的工作水头合理取值则为0~20 cm,因此分别在0~100 cm的工作水头中设置3组梯度进行研究。然而,本研究仅对黏壤土下微孔陶瓷渗灌管道的土壤水分入渗过程进行了研究,未来尚需对不同土质下的渗灌管道入渗过程及田间应用效果进行研究,以实现该技术的实际推广应用。
4 结 论
本研究采用注浆成型法制备了一种新型材料性能优良的绿色微孔陶瓷渗灌管道,并以此为研究对象,采用试验研究和数值模拟的方法,利用HYDRUS-2D模拟微孔陶瓷渗灌管道土壤水分入渗过程,为实现最优根水匹配,优化了微孔陶瓷渗灌管道工作水头。本研究的主要结论如下:
(1)HYDRUS-2D 模拟软件预测的湿润锋运移距离、累计入渗量和土壤含水量与试验结果吻合度较高,验证了模型的适用性与有效性,可较好地预测微孔陶瓷渗灌管道在不同运行管理条件下土壤水分入渗参数变化规律,为后续优化工作水头提供了可行性。
(2)微孔陶瓷渗灌管道流量在1 h 内迅速下降,待稳定后以稳定出流量持续出流,且渗灌管道稳定出流量随工作水头的增大而增大,呈显著的线性正相关关系。此外,渗灌管道附近土壤含水量最高,并沿湿润锋运移方向逐渐降低,湿润面积随入渗时间的延续逐渐增大,待入渗稳定后变化越来越小,湿润体内平均土壤含水量和湿润面积基本维持不变,仅随工作水头增加而增大。
(3)本研究对冬小麦、夏玉米和番茄3种典型密植型作物的微孔陶瓷渗灌管道工作水头进行了优化,结合密植作物的根系分布和作物生长需求情况,冬小麦推荐工作水头为0.423 m,夏玉米推荐工作水头为0.529 m,番茄推荐工作水头为0.642 m。

