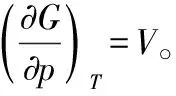大学物理化学课程中逻辑思维能力的培养示例*
邢双喜,张素铭,孙启明
(1 东北师范大学化学学院,吉林 长春 130024;2 北京师范大学化学学院,北京 100875)
物理化学是一门理论性很强的大学化学专业的基础课,整个体系涉及到很多的概念与公式,不同的公式还具有相应的使用条件,稍有差池就可能用错。同时,物理化学也是一门实验学科,很多规律的由来都是从实验数据中总结分析得到。另一方面,逻辑思维能力的培养对于学生来讲应该贯穿整个学习阶段,甚至终其一生都要重视这个问题。良好的逻辑思维能力可以帮助我们理性的判断,独立的思考以及有效的解决问题,从而更清楚的认识事情的本质和规律。物理化学这门课程具有的特点恰好可以为培养学生的逻辑思维能力提供一个适宜的平台,但是多数情况下,教师可能更注重知识的传授,往往忽略这方面对学生的训练。如果在教学过程中进行合理的设计,就可以将知识传授与能力培养有机融合,达到相互促进的双赢目标。我们在本论文中将引入一个教学示例,从而探讨如何将物理化学知识的传授与逻辑思维的训练进行有效结合。
物理化学中热力学第二定律这一章的一个重要知识点是热力学基本方程的理解与应用。目前人们针对热力学基本方程的推导及适用条件进行了多方位的探讨与分析[1-3]。由热力学基本方程延伸出对应系数关系式与麦克斯韦关系式,进一步拓展其在相关领域的灵活应用。在这方面,人们更多的注重这些关系式的记忆方法[4-5]。一般对应系数关系式是结合热力学基本方程与相应状态函数的全微分,由形式上的一一对应得到最终的八组关系式。这样处理的优点是简明直接,但在这些关系式的使用过程中还涉及到许多细节问题。基于此,我们从全微分入手,结合热力学第一定律与第二定律以及相关的推论,详细推导获得对应系数关系式。我们希望这样的推导过程一方面促进学生灵活的应用两大定律及相关的知识点,另一方面有助于培养学生分析问题与总结问题的能力,最终促进学生逻辑思维能力的提高。
1 对应系数关系式的推导
1.1 dU=TdS-pdV
在组成恒定的封闭系统中,且非膨胀功为零,U=U(S,V),其全微分如下:
这里可以引导学生思考,为什么写成这样的形式?如果写成U=U(T,V)是否可行?毕竟在之前的学习中,一直利用的这样的表达形式,所以此问题的提出,是让学生有一个总结性的判断过程,并加深对热力学基本方程的理解与应用,学会如何有目的的选择某状态函数全微分表达式的状态变量。
此外,根据教材的说明,将基本方程dU=TdS-pdV与以上全微分对照后,即可得到对应系数关系式,看上去简洁明了。但是为什么某偏导数能与某状态变量对应?它所代表的意义是什么?针对此类问题,教师可以逐步引导学生从逻辑上获得相应的答案。
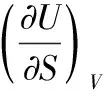
进一步理解此关系式,组成恒定的封闭系统中,非膨胀功为零的等容过程中,熵值增加,则对应的热力学能也增加,其变化幅度取决于温度的大小。这样推导出来的结果,可以让学生查询资料对于温度的表达式产生一些拓展性的思考,从而加深其物理意义的理解。在此基础上,设计相关的题目让学生进行判断是否可以利用此对应关系式进行讨论与分析。
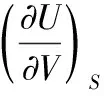
1.2 dH=TdS+Vdp
在组成恒定的封闭系统中,且非膨胀功为零,H=H(S,p),其全微分如下:
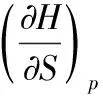
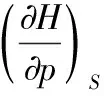
顺利完成以上两对关系式的推导之后,学生有了初步的观察、分析、概括和推理的能力,能够结合已有的知识体系,对拟讨论的问题进行判断与综合讨论。在此基础上,可以安排学生对其他四个关系式进行类似的推导,加强能力的培养,加深知识的理解与应用。以下可以为学生提供相应的参考。
1.3 dA=-SdT-pdV
在组成恒定的封闭系统中,且非膨胀功为零,A=A(T,V),其全微分如下:
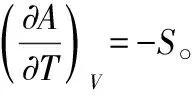
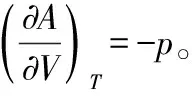
1.4 dG=-SdT+Vdp
在组成恒定的封闭系统中,且非膨胀功为零,G=G(T,p),其全微分如下:
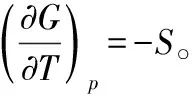
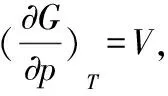
对于后面三例的讨论过程中,用到了H、A和G的定义式。从定义式进行推导的过程中,需要让学生判断可能出现的问题。比如,学生习惯性的由G=H-TS进行推导,得到dG=dH-TdS。这就是忽略了另一项的存在,把这个推导过程默认为等温变化。
2 学生反馈
我们的调查发现,通过对逻辑思维的培养,很多学生对相关公式的理解更加深入,运用起来更加熟练,在后期的作业与知识检测上更加自如。然而仍然有部分学生在这个级别的公式推导上存在很大的障碍。下面列举了随机调研中有代表性的反馈。从他们的反馈中,我们可以了解到这种“障碍”所在。
(1)一开始学习这些公式时确实使用了“死记硬背”的方法,虽然这种方法在初期看起来比较有用,公式的背诵让自己做题速度大大增加,但是这种记忆持续时间太短,用不了几天全都忘记了,又要重新记忆,到最后发现自己还是没有掌握公式的本质。
(2)单纯的记忆有一个很大的弊端,就是做题时看似速度变快了,实际上代价是思考的时间没有了,“不假思索”地写公式,计算出答案,看似很适合应试,实际上对学习没有太大的帮助。而这就很需要培养逻辑思维,就像老师课上的思路,先弄清每个物理量最关键的意义,才能进一步理解整个公式蕴含的意义。物理化学很多公式都不是简简单单的加减乘除,其中蕴涵了很深的逻辑,作为学生,必须将其掌握。
(3)通过逻辑思维的培养,我发现自己的学习时间安排发生了一定的变化——用在学习新知识上的时间变长了,而复习和完成课后作业的时间变短了,我认为这是因为在培养了对公式的逻辑思维层次的理解之后,学习的关键就从反复强化记忆转变为从新知识中提炼深层次的理解了。这样的安排大大加深了我对新知识的获取效率和掌握程度,我想对日后的学习应该是很有建设性意义的。
我们不难发现,学生们眼中的“障碍”可以理解为学生对公式的学习仍然停留在识记上(包括背公式和背推导过程),并没有很好地理解公式的本源,而后者恰好是物理化学学习的精髓所在。通过这种教学环节的实施,学生加强了对已有知识的系统性总结与概括,对公式的适用条件判断更加准确,理解更加深刻。有学生表示经过了这样的训练之后,涉及到热力学基本方程及其相关衍生公式应用方面的题目能够进行高效的分析,顺利的推导出正确的结论。与此同时,很多学生从中受到启发,逐渐培养良好的思维方式,并同其他学科联系在一起,提升自己的学习能力。
3 结 语
逻辑思维能力的培养对于学生整体素质的提高具有很积极的作用,达成良好的逻辑思维能力可以使学生具备较强的分析与解决问题的能力,增强求职的社会竞争力,拓宽人生之路。我们结合物理化学课程的特点,在教学环节中设计合理的案例,从不同的角度培养学生的逻辑思维能力,使他们在观察、判断、分析、综合以及推理等方面都受到指引,从而有所提高。在本文选择热力学基本方程对应系数的推导,在推导过程中,我们换了一种新的思路,综合运用了热力学第一定律和热力学第二定律及相关推论、热力学函数的定义式以及不同热力学函数之间的关系式、典型的热力学过程(等容过程、等压过程、等温过程以及绝热可逆过程)等。一方面巩固了所学的知识内容,对热力学基本方程的使用条件更加深了印象,另一方面锻炼了学生全面思考分析的能力。