线性代数中矩阵运算的教学设计

洪振木,朱家明

矩阵的思想最早可追溯到中国汉朝时期,中国数学家在求解线性方程组时就使用了矩阵的想法。在欧洲,18世纪或者更早些时候,行列式已被使用和计算了,到19世纪中叶推动了矩阵概念的正式提出和矩阵代数的发展。英国数学家凯莱(A. Cayley,1821—1895)和西尔维斯特(J. Sylvester,1814—1897)是矩阵论的奠基人。如今,矩阵和行列式是数学所有分支中最为重要的分支之一。伴随着人工智能、大数据技术的发展,线性代数中的基本思想、理论和方法在新工科背景下不断得到新的理解和应用,成为前沿科技的基础。线性代数在当代大学生的大学数学课程学习中起着越来越重要的作用,为后续大量课程的学习奠定了坚实的基础。因此,如何引领学生学好线性代数,深入理解和体会线性代数的核心思想和方法显得尤为重要。

线性代数围绕求解线性方程组AX=b这一核心问题,先后发展了行列式、矩阵、向量组三大研究工具。当A是方阵时,如果行列式|A|不等于零,克莱姆法则表明方程组AX=b有唯一解,并且给出了唯一解的形式;当A不是方阵时,克莱姆法则不再适用,需要根据矩阵的秩的情况来判断方程组AX=b是否有解和解的结构;若把矩阵A写成按列向量分块的形式A=(α1,α2,…,αn),则方程组AX=b是否有解的问题可转化为向量b能否由向量组α1,α2,…,αn线性表出。由此可见,矩阵及其运算在线性代数的教学中起着十分重要的作用。尽管行列式的研究要早于矩阵的研究,但大部分线性代数教材中第一章引入逆序数的概念并给出行列式的定义,这对财经类高校的学生而言,太过抽象难以理解。国内也有部分教材将矩阵作为线性代数的第一章,如电子科技大学[1]和同济大学[2]出版的线性代数教材,这对学生循序渐进学习线性代数是有利的。

目前,已有不少文献对矩阵的线性运算[3]、矩阵乘法[4-6]和逆矩阵[7-9]分别进行了一些教学设计和探索。文献[3]将矩阵运算与图像处理技术结合起来,使矩阵运算的教学可视化和生动化。文献[4]通过发生教学法对矩阵乘法的定义进行了教学设计,引导学生了解矩阵乘法的创立过程和本质。文献[5]结合大量特殊的例子对矩阵乘法的教学安排进行了优化设计。文献[6]从五个不同的角度来帮助学生理解矩阵乘法的规则,学生反馈这种教学方式极大地开阔了他们的视野。文献[7]将课程思政元素和逆矩阵的知识相结合,实现了教学中立德树人的根本任务。文献[8]中归纳总结了逆矩阵的几种不同的求解方法并进行类比探究。文献[9]从理论和实践两个角度探讨了逆矩阵的教学设计。因为矩阵的数乘可以看成一种特殊的矩阵乘法,且从某种意义上来说矩阵的乘法与逆矩阵是互为逆运算的,所以矩阵的线性运算、矩阵的乘法和逆矩阵这三部分内容是一个密切联系的整体。故本文将矩阵的线性运算、矩阵的乘法和逆矩阵进行统一的教学设计,对矩阵运算的由来和本质进行深入探究,增强矩阵运算与现实生活中应用实例之间的联系,并且注重培养学生数形结合的思想,以启发式的教学激发学生的学习兴趣和创造力。

1 矩阵的线性运算

矩阵的线性运算难度不大,但如何让学生快速理解并建立起线性代数的学习兴趣非常重要。学生往往对如何学习线性代数和线性代数在生活中有什么应用会有很多疑惑,教师要尽量帮助学生用更科学更直观的方式建立线性代数与日常生活的联系,这样的例子要既简单又生动,而图像的处理和动态展示就是很好的教学素材。

在计算机中二值图像对应的是元素为0和1的矩阵,灰度图像对应的是元素为0至255的矩阵,而彩色图像可以看成是由元素为0至255的3个矩阵合成的,每个矩阵分别对应红色、绿色和蓝色三个颜色通道的灰度值,每个像素分别对应红色R、绿色G、蓝色B三个分量。因此,图像背后对应就是矩阵,对图像的处理就是对相应矩阵的处理。

在教学设计的时候,如图1所示,可以通过神舟十五号载人飞船发射画面的图像处理,作为案例导入教学,分别展示提高或降低图像亮度、提高或降低图像的对比度、反映发射瞬间红色增强的画面等与原始图像的对比图,让学生带着问题去学习,待讲完矩阵的加法和数乘的定义与运算规则之后再启发学生思考图像处理背后的数学原理。此外,引入神舟十五号载人飞船发射的画面可以自然地过渡到课程思政的教学,进而增强青年学生的民族自豪感和自信心,厚植学生的爱国主义情怀。

图1 神舟十五号飞船发射画面

设矩阵A=(aij)表示灰度图像所对应的矩阵,其中0≤aij≤255。设J是与A同型的元素全为1的矩阵,0<λ<255,0≤μ≤255表示数。则A+μJ和A-μJ分别对应提高和降低图像整体的亮度;当λ>1时,λA对应提高图像的对比度;当λ<1时,λA对应降低图像的对比度。

对于一幅彩色图像,如果矩阵A1、A2、A3分别对应于该图像的红色、绿色和蓝色通道的灰度值,那么对这三个矩阵的线性运算就对应于该彩色图像的处理。如A3+μJ表示对图像的蓝色进行增强,λA2表示增强图像绿色的对比度,对A1、A2、A3同时进行上述操作表示增加图像整体的亮度或提升整体的对比度。如图1所示,对于i=1,2,3,Ai+60表示提高亮度,1.8Ai表示提高对比度,A1+90J实现红色增强。在课堂教学时,可以启发学生思考如何消除彩色图像中的某种颜色。

设矩阵A表示世界名画梵高的画像,矩阵B表示世界名画蒙娜丽莎的画像,矩阵A和B的线性运算结果(1-λ)A+λB(0≤λ≤1)表示合成的图像,伴随着系数λ从0变到1,如图2所示可以观察到图像将由梵高逐渐转变为蒙娜丽莎。课堂教学时可以利用Matlab软件实现图像的动态变化,并做成动画,让学生直观而震撼地感受到线性代数的魅力。作为课后练习,公布程序代码可以帮助感兴趣的同学实现更多的图像处理效果。从课堂的教学效果来看,图像处理引入矩阵线性运算的教学深受学生喜爱,学生学习的积极性和主动性明显增强。

图2 梵高和蒙娜丽莎画像

2 矩阵的乘法

2.1 矩阵乘法定义的由来

英国数学家凯莱研究了线性变换的复合,并定义了矩阵乘法,以便复合变换的系数矩阵刚好为矩阵乘以矩阵的乘积。根据下述两个线性变换

可以得到

可以定义矩阵的乘法C=AB,即

上述定义可以推广至更一般的两个矩阵的乘积AB,由此可知矩阵乘积并非两个矩阵对应元素相乘。数学定义的引出往往是为了解决实际问题而提出的,矩阵的乘法是为了表示复合变换的系数矩阵而提出的,从而回答学生矩阵乘法为什么不是对应元素相乘的疑惑。此外,由于两个线性变换中公共未知量的个数是相同的,故要求矩阵A的列数与矩阵B的行数相等也就十分自然了。因此,要鼓励学生学会透过现象看本质,理解矩阵的乘法本质上是两个线性变换的复合。同时,由特殊的2阶矩阵乘法的定义过渡到高阶矩阵乘法的定义蕴含着由特殊到一般的数学思想。

2.2 矩阵乘法与线性变换

在讲授矩阵乘法的运算法则和性质之后,可以再次引出线性变换Y=AX的定义,并将线性变换限定为特殊的旋转变换加以举例,通过数形结合的方式介绍旋转变换,如图3所示。

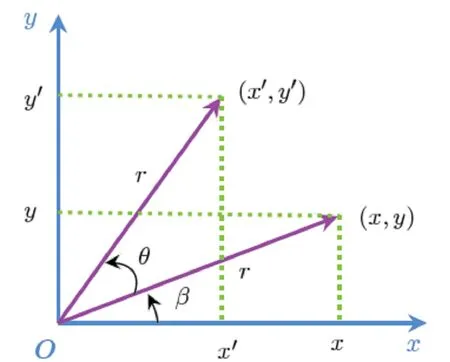
图3 逆时针旋转变换

由图3容易推出

因此,在平面直角坐标系中,线性变换

是将点(x,y)逆时针旋转θ角得到新点(x′,y′)的旋转变换。这可以启发学生以数形结合的方法来学习线性代数,并思考逆时针旋转kθ角和顺时针旋转θ角所对应的旋转变换矩阵。旋转变换在计算机图形学和动画演示中有非常重要的应用,教学时可以制作一个旋转的动画进行展示,让学生感受到线性代数在生活中的应用,激发学生的学习兴趣。图4展示了房子逆时针旋转45°、90°和180°的图像。

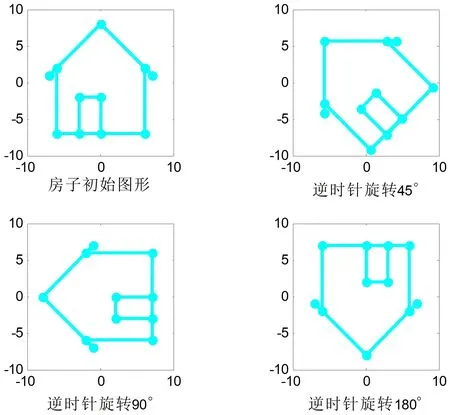
图4 房子逆时针进行旋转

考虑两个旋转变换的复合,即对一个图形先绕原点逆时针旋转β,再继续绕原点逆时针旋转α,它们的复合对应着将原图直接绕原点逆时针旋转α+β。因此,

这给出了三角函数和差化积公式的另一种理解和记忆方式,也与凯莱给出的矩阵乘法定义相呼应。

不难发现,交换复合的旋转变换中两个旋转变换的顺序,不会改变复合变换的最终结果,这表明两个旋转变换的矩阵是可交换的。在教学中可以启发学生思考线性变换的复合是否可交换。简单地观察可以知道逆时针旋转60°的变换与沿X轴旋转180°的变换进行复合是不可交换的,即

从而导出矩阵乘法通常不满足交换律。进一步,还可以引导学生将矩阵乘法的性质与数的乘法的性质进行类比,探究两种运算之间的异同点,进而学会使用类比的思想来学习后续课程内容。

2.3 矩阵乘法的应用

作为矩阵乘法的应用,在线性代数的一些教材中,讲授矩阵的乘法时会介绍职工轮训或神经网络的应用实例[1]。对于财经类高校或偏文科类的高校,教师在讲授时可以根据学生的接受程度不同,选择介绍下述这个简单直观的实例。考虑下述多项式的乘积

(2x2+5x+3)(3x4+2x3+6x2+x+4)=

6x6+19x5+31x4+38x3+31x2+23x+12,

该多项式的系数也可以用矩阵的乘积来表示:

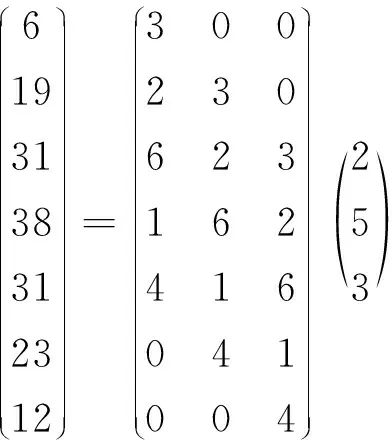
在Matlab软件中,正是利用这样的想法来计算两个多项式的乘积的,这与信号的卷积也有密切的联系。由本例可知,事物之间是普遍联系的,鼓励学生在学习时要不断尝试将新的数学概念和数学理论与已有的知识建立联系,以达到融会贯通的效果。

3 逆矩阵

从某种意义上说,求可逆矩阵的逆矩阵是矩阵乘法的逆运算,但不少学生对于逆矩阵的定义中为什么要求AB=BA=I不是十分理解。为了使得学生容易接受,在这一部分教学内容进行设计的时候,可以先导入情报加密解密这一案例,启发学生一起探索如何定义加密矩阵和解密矩阵才能完成加密和解密的过程。

3.1 由案例导入逆矩阵的定义

在介绍逆矩阵的定义之前,可以先展示电影《永不消逝的电波》的剧照或电影片段。询问学生第一眼看到这幅图片的时候,是不是马上就会联想到谍战影视剧中情报人员通过无线电波进行情报的传输?是否对情报是如何加密和解密的感到好奇?

由此引出可以通过线性代数中的方法来进行情报的加密和解密。假定需要传输的情报内容为英文字母,为了方便先将26个英文字母分别与1到26建立一一对应关系。不妨设需要传递的明文X是一个3阶矩阵。而在情报的传输过程中,一般不能将明文X直接进行传输,需要对明文X进行加密,将加密后的密文C进行传输。一个比较有效的方法是发送者在明文X的左边或右边乘以一个加密矩阵A,将X转化为密文矩阵C。当接收者接收到密文C后,再通过解密矩阵将密文C转化为明文X。

如果事先约定好加密矩阵A,当接收者接收到密文C时,如何求得明文X呢?

当AX=C时,如果有BA=I,那么在等式AX=C的两端同时左乘B,可知X=BAX=BC。当XA=C时,如果有AB=I,那么在等式XA=C的两端同时右乘B,可知X=XAB=CB。

因此对于加密矩阵A而言,如果存在矩阵B使得AB=BA=I,那么将B作为解密矩阵是十分合适的。由此可以自然地给出逆矩阵的定义,而由加密矩阵和解密矩阵是互相唯一确定的,又可以引出逆矩阵唯一性的证明。此时,再假定加密矩阵

抛出如何进行解密求出明文X这一问题,待本节内容讲授完毕之后再给出解答,让学生带着如何解密这一实际问题来学习逆矩阵这一节的内容。

3.2 逆矩阵与旋转变换

在讲授矩阵乘法时,已经介绍了将点(x,y)逆时针旋转θ角得到新点(x′,y′)的旋转变换。本节讲授逆矩阵的定义和唯一性之后,可以引导学生思考顺时针旋转变换所对应的矩阵是什么?

一个自然的想法,将点(x′,y′)逆时针旋转2π-θ角可回到点(x,y)。而逆时针旋转2π-θ角相当于顺时针旋转θ角。因此

是将点(x′,y′)顺时针旋转θ角回到点(x,y)的旋转变换。容易验证下述等式

即逆时针旋转变换所对应的矩阵与顺时针旋转变换所对应的矩阵恰好互为逆矩阵,并且这两个矩阵是可交换的。这从图形的旋转上很容易佐证这一点,进一步引导学生学习线性代数时多用数形结合的方法。为了更好地展示这一点,可以利用Matlab将图形逆时针连续旋转180°变换后又顺时针旋转180°回到初始位置这一过程制作成动画,加深学生对逆矩阵的理解。图5分别展示了将房子初始图形逆时针旋转60°(A)、沿x轴翻转180°(B)、先逆时针旋转60°再沿x轴翻转180°(BA)、先沿x轴翻转180°再逆时针旋转60°(AB)的效果图。在介绍逆矩阵的性质(AB)-1=B-1A-1时,可以借助图5来进行解释,将图5中右下图恢复到房子初始图形,必须先顺时针旋转60°(A-1)再沿x轴翻转180°(B-1)。同时,注意到这里AB≠BA也表明矩阵乘法不满足交换律,与前文呼应。

图5 房子旋转与翻转效果图

3.3 华罗庚恒等式

在介绍了逆矩阵的性质之后,可以适当增加教学难度,介绍华罗庚恒等式,带领学生一起欣赏该恒等式并加以证明。

华罗庚恒等式:设A,B,AB-I均是n阶可逆矩阵,则(A-B-1)-1-A-1也是可逆矩阵,且[(A-B-1)-1-A-1]-1=ABA-A。

因为B和AB-I可逆,所以(ABI)B-1=A-B-1也可逆。只需验证(ABA-A)[(A-B-1)-1-A-1]=I.在证明的过程中ABA-A=ABA-AI=ABA-ABB-1这一步是关键。因此可以提醒学生关注单位矩阵发挥的重要作用,学做单位矩阵式的人物,哪里需要去到哪里。而对于[(A-B-1)-1-A-1](ABA-A)=I的验证则可以留作课后练习。

华罗庚恒等式的证明难度相对于教材中例题的证明难度要大一些,这也表明该恒等式的发现过程更加困难。由此自然地介绍华罗庚教授传奇的一生,开展课程思政教学,号召学生学习“华罗庚精神”,学习他一心报国、矢志不渝的爱国精神,逆境拼搏、奋斗不息的自强精神,慧眼识珠、甘当人梯的人梯精神,生命不息、战斗不止的奉献精神。鼓励学生打好数学基础,将来为祖国的科技进步贡献力量。

3.4 逆矩阵与密文解密

在讲授完利用矩阵的初等变换求逆矩阵之后,可以举例呼应本节开头提到的加密解密原理。设加密矩阵

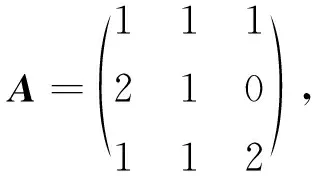
要求出解密矩阵B=A-1,可以将(A,I)进行初等行变换化为(I,A-1),则X=A-1C。不难求得

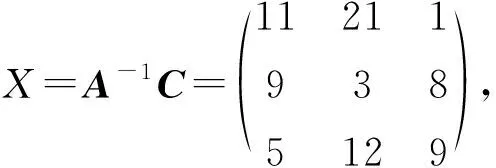
4 结语

本文主要介绍矩阵的加法和数乘、矩阵的乘法、逆矩阵的教学设计,将矩阵的加法和数乘与图像的亮度和对比度建立联系,理解数字图像处理背后的数学原理;厘清矩阵乘法定义的由来,通过旋转变换来理解矩阵乘法的本质,用矩阵乘法来求出多项式乘积的系数;通过情报加密和解密的过程引出逆矩阵的定义,并通过解密矩阵的求解完成情报的解密,通过数形结合导出旋转变换的逆变换,求逆矩阵时给出华罗庚恒等式并介绍华罗庚精神,厚植学生的爱国主义情怀。通过这些设计,建立图像与矩阵之间的联系,并将其贯穿于矩阵运算的教学中,传递数学问题来源于生活且数学研究应用于生活这一理念,更好地帮助学生理解线性代数中的基本运算及其在生活中的应用。从教学效果来看,这些教学内容的设计和数学思想的传递,极大地提高了学生的学习兴趣,激发了学生的想象力和创造力,丰富了矩阵运算的教学内容。