基于Simulink与CoppeliaSim一级倒立摆建模与仿真

纪鸿宇,张 新,张洪彪,张 涛

1 引言

20世纪50年代,麻省理工学院专家从火箭发射助推器原理抽象出倒立摆模型,并利用倒立摆研究各类欠驱动系统控制算法性能,并将其应用到各种工业和生活场景,如:平衡车平衡控制、海洋钻井系统稳定控制、双足机器人行走平衡控制等[1]。

倒立摆按照结构可分为直线倒立摆和旋转倒立摆,按照摆杆的数目可分为一级、二级和三级倒立摆。倒立摆是一个典型的欠驱动系统,即驱动机构的数量小于自由度,其本质上是一个非线性系统[2],对于非线性系统的控制算法设计一直以来是控制领域的热点。

倒立摆控制可分为起摆和稳摆两个阶段。在起摆控制器设计方面,Razban等[3]使用能量起摆控制器,实现一级倒立摆由自然下垂到摆起稳定的整个过程,并设计了加权过渡函数,解决了起摆控制器到稳摆控制器易超调、抖动的现象;魏帅[4]设计了一种类似于“开关控制”的bang-bang控制器,也可使倒立摆完成起摆动作。在稳摆控制器设计方面,王丽琴[5]设计双闭环PID控制器实现了一级倒立摆的平衡控制;常昊天等[6]使用模糊PID对二级倒立摆控制稳定性进行研究,利用模糊控制器对PID参数自适应调整,取得了良好的动静态性能;胡乐乐[7]以二级倒立摆为研究对象,设计了LQR(Linear Quadratic Regulator)控制器,利用Matlab仿真,通过超调量、稳定时间等指标用来衡量控制器的响应性能,性能良好;董如意[8]使用遗传算法和改进的遗传算法对一级倒立摆进行控制,改进的遗传算法解决了传统的遗传算法搜索速度迟缓,易陷于局部最优,易早熟问题;何卫东等[9]融合深度强化学习和深度学习方法,有效地建立倒立摆状态和执行动作的映射关系,从而实现倒立摆的运动控制。

本文结合能量控制器和LQR控制器,实现直线一级倒立摆起摆到稳摆整个过程。首先,建立了一级倒立摆的数学模型。其次,通过Simulink与CoppeliaSim联合进行动态可视化仿真,不断优化控制器参数,提高开发效率。最后,设计仿真实验。与文献7中纯理想状态下仿真相比,第一,该法中的实体物理模型考虑实际系统的各种阻尼、电机的驱动能力和刚体碰撞等因素,比传统数学模型的参数更精确,仿真结果能够更准确地模拟实际系统;第二,可直接观察摆杆的运动轨迹和各关节的运动参数,直观性大大增加;第三,由于仿真结果与实际系统保持高度一致,可将开发的控制器和相关参数部署到运动控制卡等硬件中,为后续硬件开发降低开发周期和人工试错成本。仿真结果表明,该设计方法具有可行性和高效性。

2 倒立摆建模

一级倒立摆的理论模型如图1所示的小车和摆杆的模型组成,其主要由一个移动副,一个转动副构成,而其输入力仅由F提供,为典型的欠驱动系统。

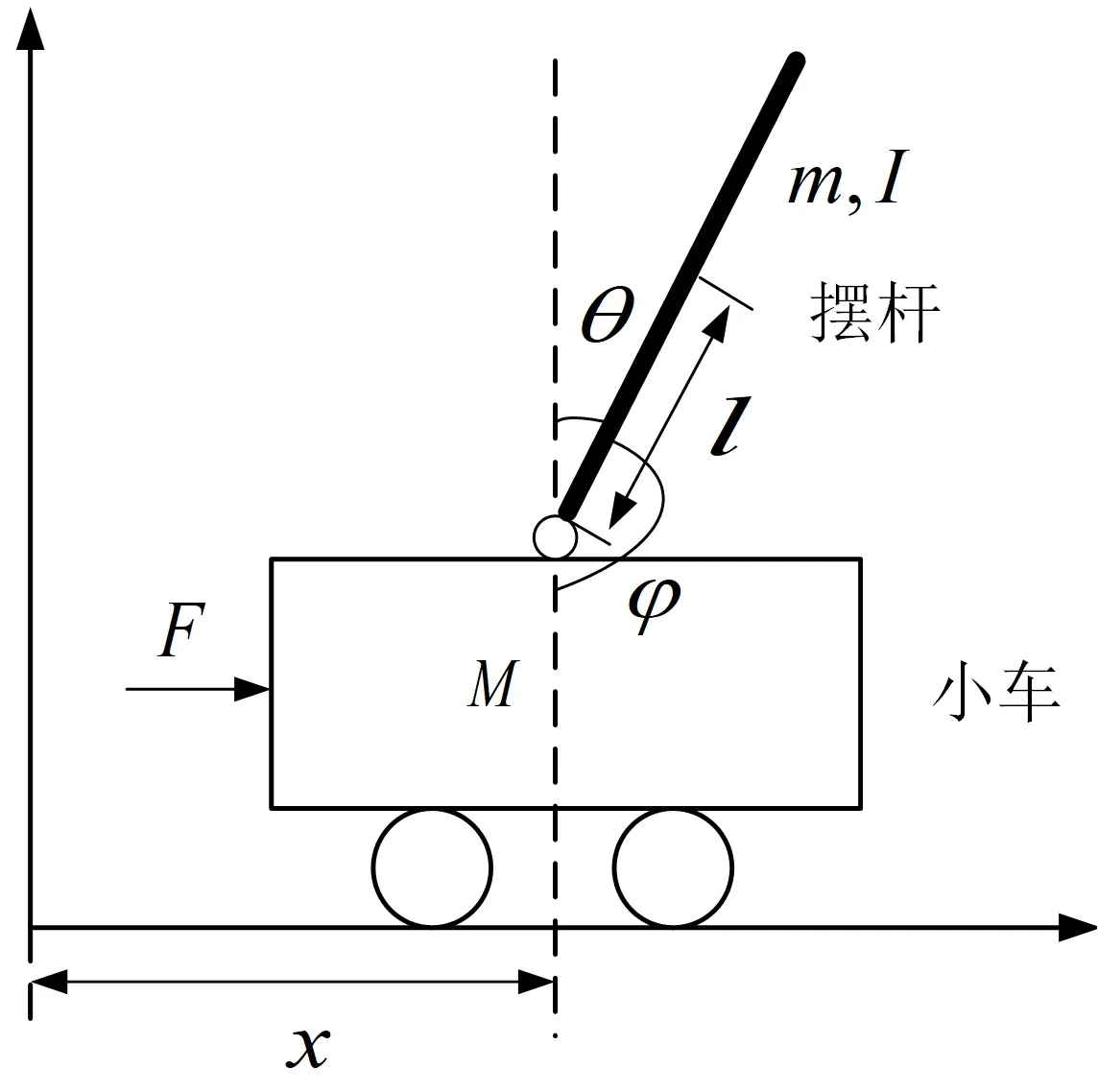
图1 倒立摆模型

实际系统模型相关参数定义如表1所示。

表1 一级倒立摆系统参数

利用拉格朗日方法建模,拉格朗日方程为:

(1)

其中:L为拉格朗日算子,q为系统的广义坐标,T为系统的动能,V为系统的势能。

拉格朗日方程可变式为:

(2)

在式(2)中,fi为系统在第i个广义坐标系上的外力。在一级倒立摆系统中,系统有两个广义坐标,分别为x和θ。

沿系统的广义坐标θ方向上不受外力,沿着系统的广义坐标x方向受到外力F,因此该系统对应的拉格朗日方程为:

(3)

在一级倒立摆系统中L为:

L=T-V

(4)

(5)

当θ在[-0.056π,0.056π]中时,经线性化并整理得到系统的状态方程并代入系统参数得:

(6)

(7)

3 控制器设计

倒立摆在重力作用下自然下垂(φ=0°),在没有施加外力情况下,由电机驱动小车带动摆杆往复摆动直至使摆杆能倒立平衡,这是一个非线性过程。本文采用的是能量控制器和LQR控制器切换的策略,摆杆从下垂摆动到目标切换角度时(φ=±160°),采用能量控制器,其结构简单、易用,本质上将非线性控制转化为开环控制,无需精确的控制量,这样避免了复杂的非线性控制器设计。摆杆从目标切换角度到倒立平衡角度(φ=±180°),采用LQR控制器,当θ在小角度范围内,θ以切代弧处理,将非线性控制转化为线性控制。下面将分别介绍。

3.1 能量起摆控制器

能量起摆控制器主要是通过对摆杆的能量控制代替对小车速度环或位移环的控制[10],使小车在有限的直线导轨上往复运动,同时带动与其相连的摆杆自由转动。

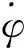
图2 摆杆起摆不同状态

设摆杆绕轴转动惯量为:J=I+ml2,则摆杆的力矩平衡方程为:

(8)

假设倒立摆在平衡位置时能量E0=0,在运动中倒立摆的总能量E为:

(9)

摆杆的能量变化为(对式(9)进行求导并联立式(8)):

(10)

构造李雅普诺夫函数(Lyapunov Function),并设计基于李雅普诺夫函数控制律[11],其流程如下所示:

设李雅普诺夫函数为:

(11)

(12)

代入式(10):

(13)

设计起摆控制器,令系统控制输入u为:

(14)

其中k为系统的能量反馈系数,通常取±1,具体正负号取决小车运动方向与目标驱动方向是否相同。

联立式(13)(14):

(15)

只要摆杆的角度θ不为0或±π/2,则dV/dt>0,系统的能量会一直增加,直至收敛于0,考虑在实际中直线导轨为有限长,因此需对系统的输入限幅,所以系统的输入表达式为:

(16)

其中:

3.2 LQR稳摆控制器

倒立摆在稳摆时经过线性化处理,LQR恰为线性二次型调节器,并且该算法易于处理和计算。LQR的控制原理如图3所示,A、B、C分别为式(5)中状态方程的系统矩阵、控制矩阵和输出矩阵,u为倒立摆的控制信号,即加速度,K为LQR的反馈增益矩阵。

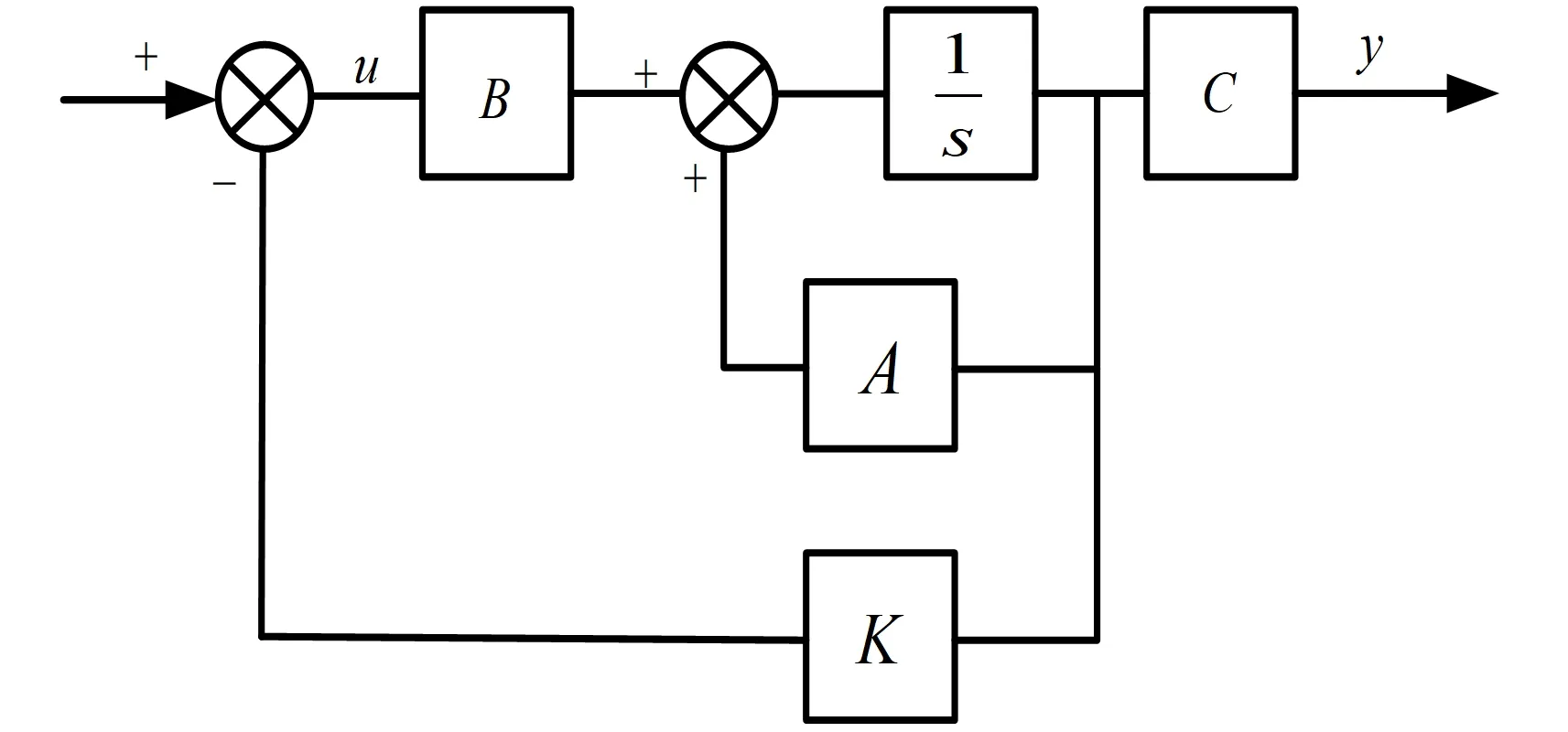
图3 LQR原理图

引入二次型最优控制性能指标J′,通过对控制量u使得:

(17)

为最小,在式(17)中Q和R分别是系统状态变量和输入变量的加权矩阵。

根据线性二次型理论,若想系统鲁棒性最强,即J′最小,则控制信号应该为:

u(t)=-R-1BTP(t)x(t)=-Kx(t)

(18)

式(18)中P(t)为黎卡提(Riccati)方程[12]的解,K为LQR最优增益矩阵。在实际中调用Matlab的lqr(A,B,Q,R)指令即可求得LQR增益K,可省去繁琐的计算过程。

4 仿真结果与分析

4.1 联合仿真模型及参数设置

CoppeliaSim具有很强的多体运动学和动力学仿真优势,但是不适合三维模型建模[13]。鉴于此,先在SolidWorks建立出三维模型,赋予小车、摆杆的材料属性(如图4所示),设置零件配合关系,进而通过urdf生成工具导出urdf文件,再将urdf文件导入到CoppeliaSim环境中。此时,倒立摆在CoppeliaSim环境中(如图5所示)拥有了几何尺寸、质量、转动惯量、重力加速度、约束关系等相关属性参数。CoppliaSim有着完善的物理仿真引擎,仿真程度极高,这可以更好地模拟实际倒立摆系统。

图4 SolidWorks小车摆杆材料设置

图5 CoppeliaSim环境下倒立摆

Simulink是基于Matlab的一种可视化仿真开发工具,以各种功能不同的模块相结合来实现仿真功能,具有拓展性强、灵活性强、交互式建模和仿真的特点,便于开发者快速建立模型[14]。

采用Simulink与CoppeliaSim联合开发相比较于使用Lua语言直接CoppeliaSim环境中开发控制器,Simulink图形化编程开发简单,降低了算法开发门槛,且算法模型可读性强、便于管理,算法运行效率高。通过远程的API接口,Simulink与CoppeliaSim进行Socket通信可实现极低延时的远程信息数据交互,CoppeliaSim中的倒立摆不断的接收Simulink中的控制指令,驱动倒立摆小车运动,实现倒立摆的精准的运动控制,即实现了控制系统与机械系统的联合仿真。

首先,在Simulink环境下搭建上述能量起摆控制器和LQR稳摆控制器(如图6所示),然后将Simulink与CoppeliaSim的仿真步长均设置为10ms、仿真周期设置为无穷大,最后两者通过API接口进行通讯。具体控制流程为:摆杆在自然下垂φ为0度,通过一个脉冲信号激励,系统先进入到起摆控制器,小车带动摆杆往复运动,当φ绝对值大于160度时,系统切换到稳摆控制器,最后摆杆倒立保持平衡且小车在原点位置。

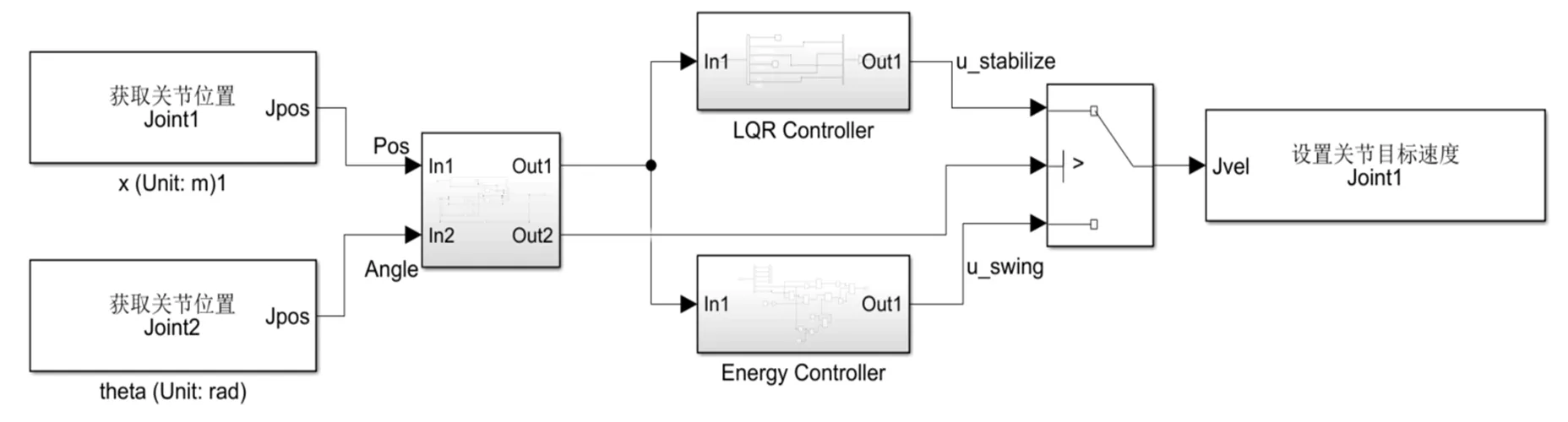
图6 Simulink环境下所搭建的控制器

4.2 仿真结果

仿真过程中小车实际运行方向与预设方向相反,因此在能量控制器中设置k=-1;根据上文所述,在LQR控制器中R=[1],对于Q矩阵采用人工经验试凑法整定。在多组数据中选择具有代表性的5组数据(表2)分析,其中K经计算分别为:

表2 控制器参数

4.2.1 仿真实验1:起摆与稳摆

采用能量起摆控制器和LQR稳摆控制器实现倒立摆由摆起到倒立平衡。

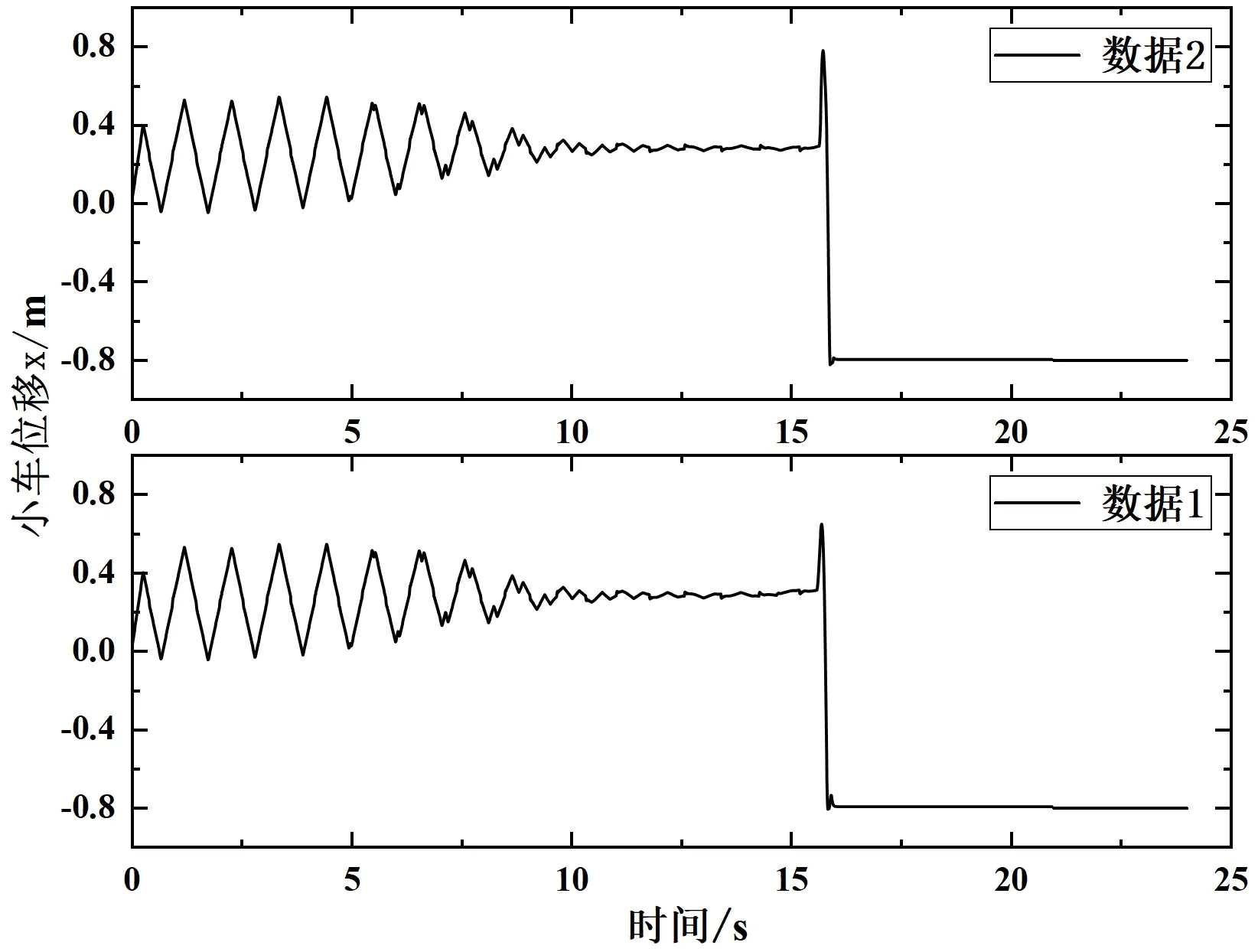
图7 数据1、2位置x响应曲线

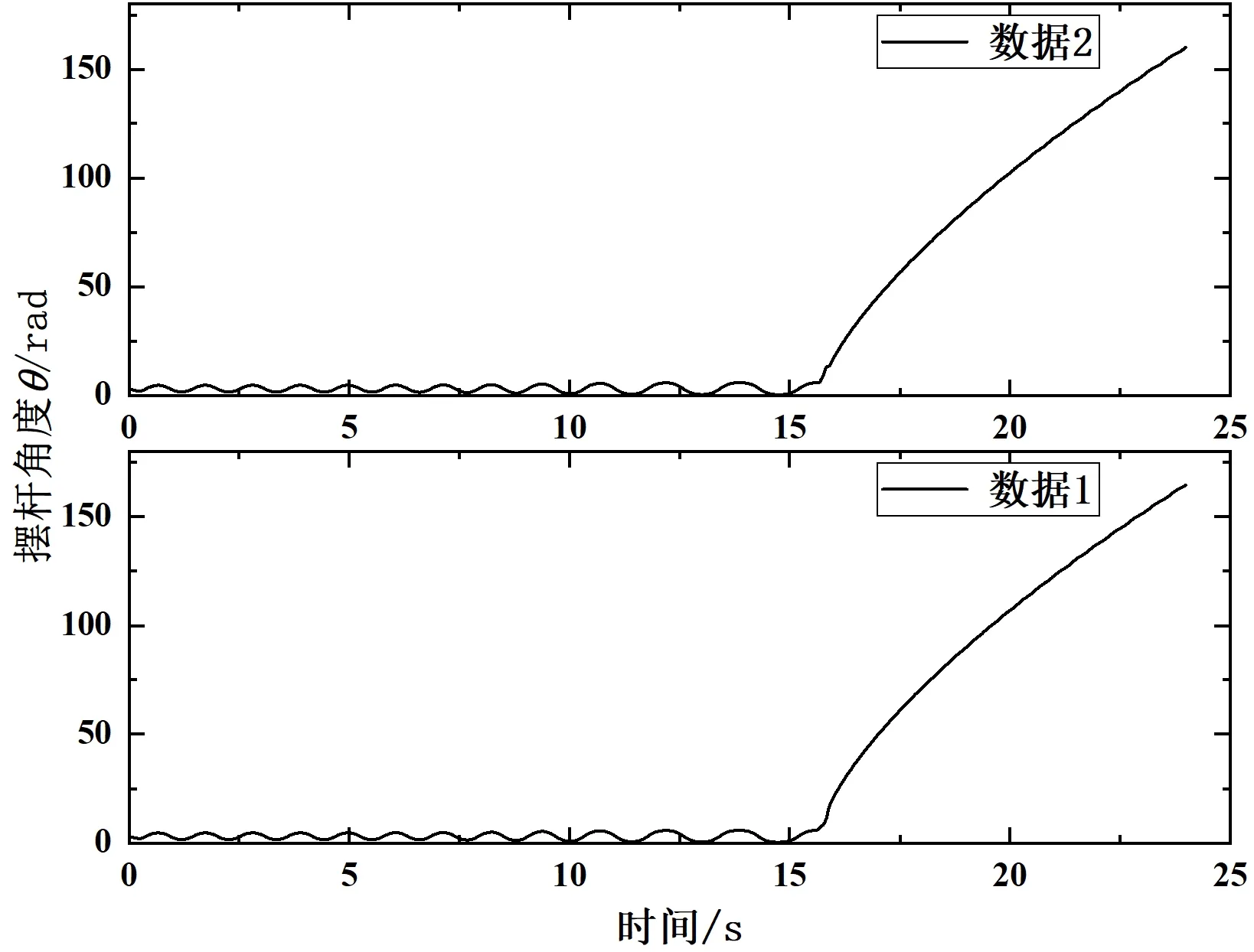
图8 数据1、2角度θ响应曲线

从图7、图8中可以看出,倒立摆在摆起的过程中,随着摆杆的往复运动,小车位移由大变小,即系统的能量虽在增大,但增大的速率在变小,在16s左右处为能量控制器向LQR控制器切换状态,但由于参数不合理导致系统没有进入稳态。结合图7中数据2以及在CoppeliaSim的动画,在切换控制器时,小车失控,第一次直接撞上一侧限位(小车两端限位为±0.8m),接着撞上另一侧限位停止,摆杆处于单方向旋转状态;相较于数据2,数据1中Q矩阵对应的状态变量x权重较小,在切换控制器时,小车第一次没有撞上限位,之后撞上一侧限位停止,摆杆处于单方向旋转状态。

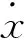
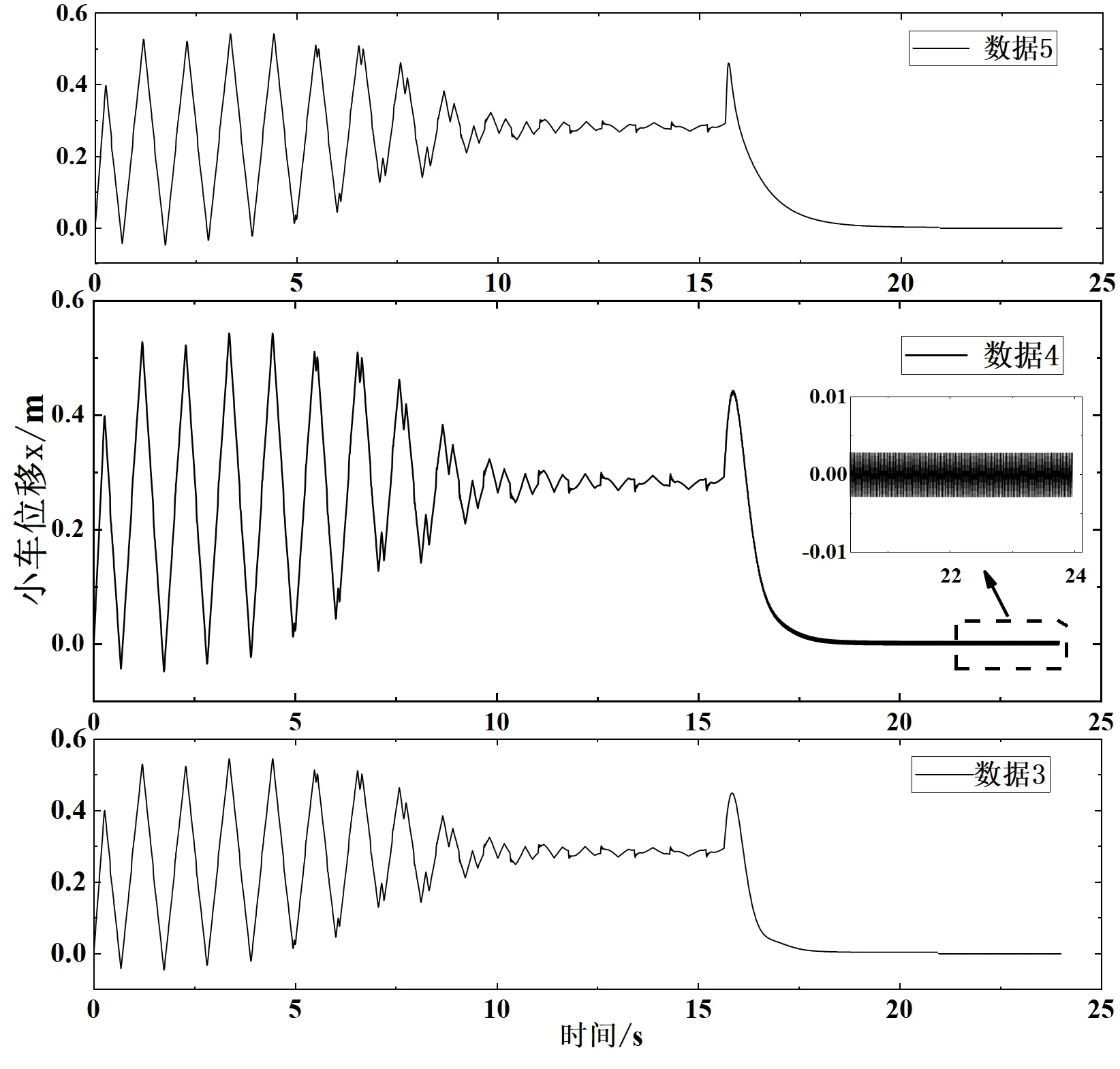
图9 数据3～5位置x响应曲线

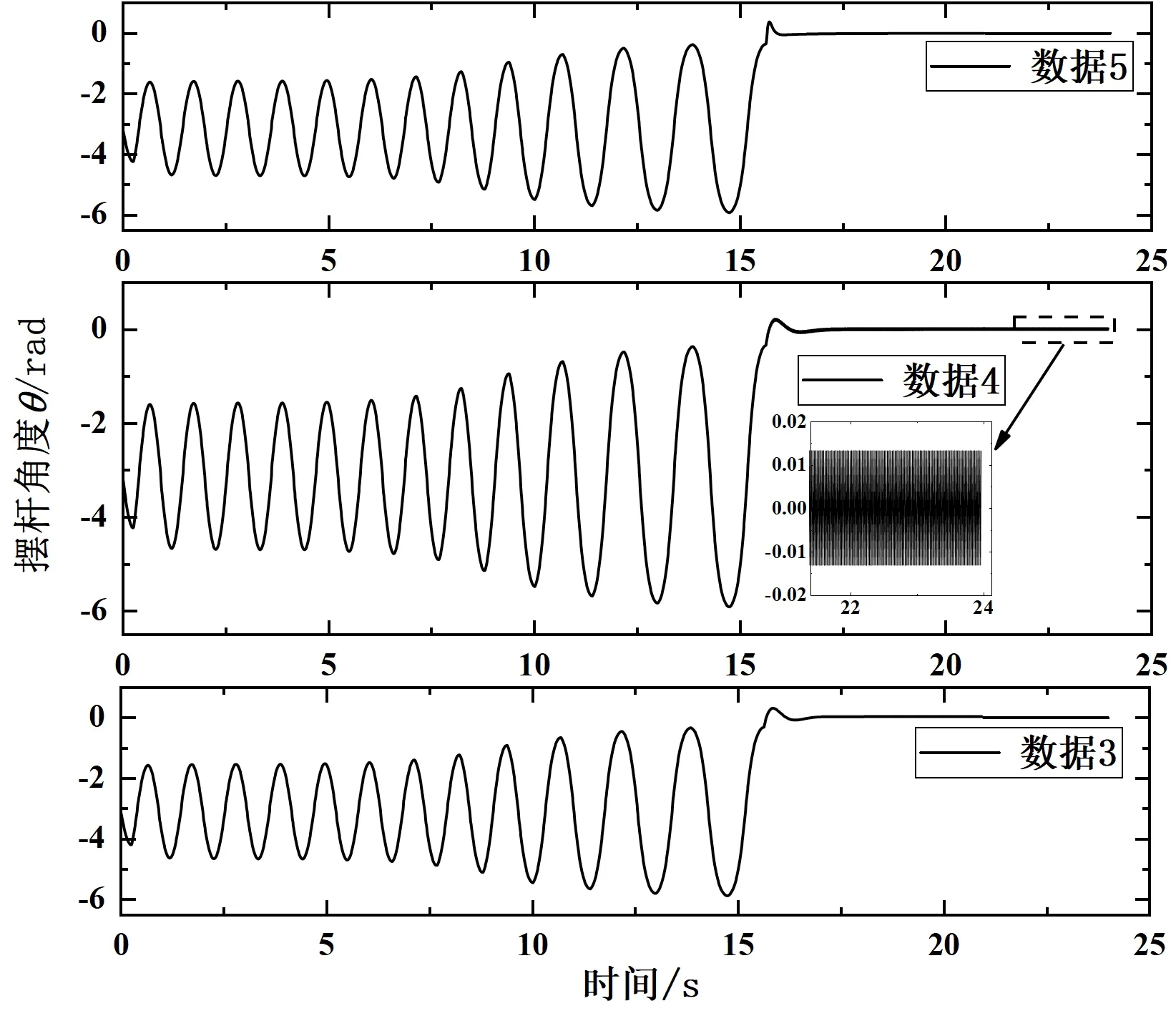
图10 数据3～5角度θ响应曲线

4.2.2 仿真实验2:有扰动时平衡控制

为验证LQR控制器的抗干扰能力,选取表2中数据3和数据5作为LQR控制器的参数,使用相同的干扰信号,即在倒立摆稳定过程中1.6s附近增加一个脉冲信号干扰,取状态变量为θ=0.056π,系统在两组在不同参数的LQR控制器作用下均能够返回到初始状态,系统受到扰动后位置响应曲线如图11所示,角度响应曲线如图12所示。分析计算系统响应数据得出:数据3对应的系统调节时间为3.22s,摆杆超调量为0.17453rad;数据5对应的系统调节时间为3.43s,角度的超调量为0.17453rad,数据5相较于数据3对应的控制器响应更快,且小车运动平稳,摆杆能够快速进入稳态当中,由此可见LQR控制器的抗干扰能力强、响应速度快,在倒立摆系统中体现出良好的鲁棒性。

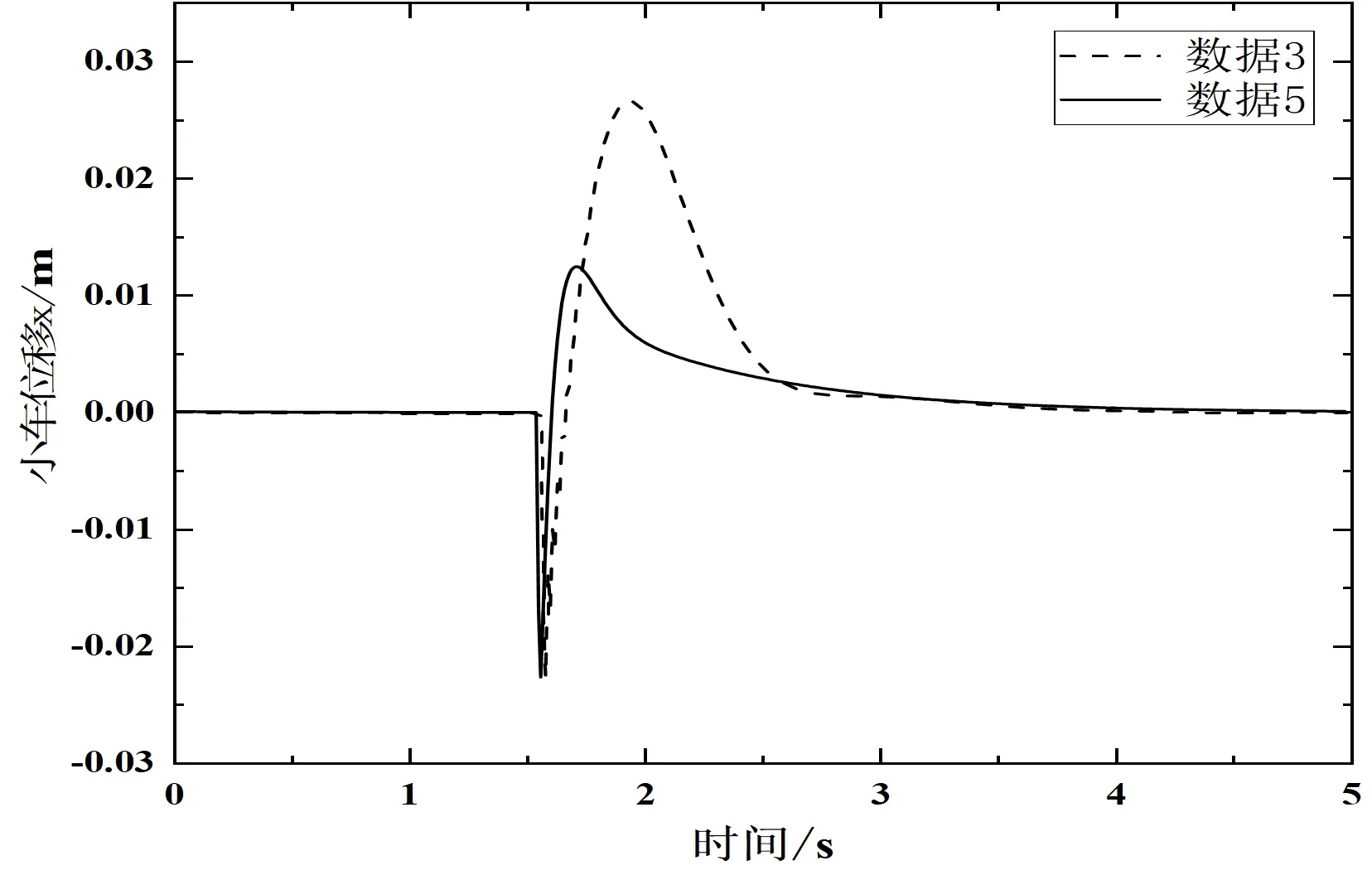
图11 数据3、5受干扰后位置响应曲线

图12 数据3、5受干扰后角度响应曲线

5 结论

本文提出了一种基于Simulink与CoppeliaSim来设计直线一级倒立摆控制器的方法,实现了倒立摆由能量起摆到LQR稳摆控制。首先,采用牛顿力学和拉格朗日法建立倒立摆的数学模型;其次,在Simulink中设计了能量起摆控制器和LQR稳摆控制器,同时在CoppeliaSim中建立实体模型,二者通过API接口联合仿真,通过直观地观察仿真动画,并分析响应数据,不断优化控制器参数,使控制器达到较佳的响应性能,这样可以减少失败风险,降低开发成本。仿真实验结果表明:所设计的能量起摆控制器和LQR稳摆控制器可实现良好的过渡,LQR控制器具有振荡幅度小、响应速度快、鲁棒性强的优点。同时也表明该设计方法的可行性与高效性,为后续硬件开发提供了理论基础。