基于混合遗传禁忌搜索算法的多机器人任务分配

周 航，秦实宏，方泾丞

（武汉工程大学 电气信息学院，武汉 430205）

伴随着电子商务在最近几年的迅猛发展，以适应仓储物流行业发展的需要，建设更加智能化的自动化仓储系统已经成为当前研究热点。其中，以AGV（automated guided vehicle）为代表的智能搬运机器人是自动化仓储系统的关键组成部分，在降低物流成本、降低工人劳动强度、提高物流效率等方面起到了举足轻重的作用。现代仓储系统已经逐步过渡到“货到人”的运作模式[1]，对于分拣效率、分拣精度等方面也都有较高的要求，而多机器人的任务分配是关系到仓储运作效率的核心问题。

目前，国内外很多学者都采用不同算法对任务分配问题进行了研究。文献[2]引入局部最优变异算子和融合改进的模拟退火算法对蚁群算法进行改进，解决了多机器人的任务分配问题。文献[3]采用时间窗法构造了一个多AGV 调度系统，该系统能够有效地解决AGV 之间的冲突和死锁问题，具有较好的实时性和稳定性。文献[4]针对多AGV 的货架任务分配问题，提出一种混合蚁群遗传算法，该算法对遗传算法的局部搜索能力有很好的改善作用。文献[5]提出了在复杂环境下进行多机器人任务指派时，将产生维度灾难，针对强化学习中灾难问题，提出了基于启发式的深度Q 学习算法。文献[6]提出了一种结合遗传算法和滚动调度的多机器人任务分配算法，以解决大规模的包含任务优先级约束的多机器人任务分配问题。文献[7]在考虑多种仓储作业模式的基础上，提出一种改进的多种群遗传算法来求解总作业时间最小的多AGV 任务分配模型。

基于以上研究内容，本文针对仓储多机器人任务分配问题，提出了一种混合遗传禁忌搜索算法。该算法利用禁忌搜索算法中的禁忌表和藐视准则对遗传算法每次迭代后的种群进行优化调整，既保留了遗传算法强大的全局搜索能力，又加快了收敛速度，还避免其易陷入局部最优的问题[8]。

1 问题描述与模型建立

1.1 问题描述

机器人任务分配是指将区域内的任务点无重复地分配给各个机器人，并使机器人在满足目标约束的前提下达到最优结果。本文以仓储机器人为研究对象，以机器人配送成本最小为目标建立数学模型，该模型可以转化成VRP 模型进行求解。假定仓储环境是一个二维的空间，用栅格法建立环境模型，所述环境包括分拣台、货架、空载机器人、载货机器人和充电桩。初始状态时，机器人位于充电桩位置，可以接收任务订单。一旦接收到任务，机器人会移动至对应货架位置，以及按指定的次序把货物搬到分拣台。机器人在电量不足或者完成全部工作时，机器人会重新回到充电桩。自动化仓储模型如图1所示。

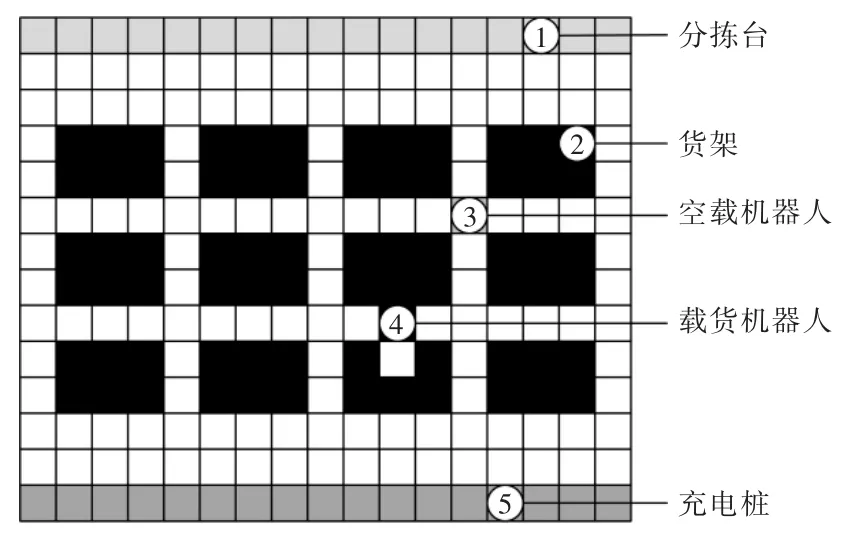
图1 自动化仓储模型Fig.1 Automated warehousing model

为了方便对模型进行求解，本文针对机器人在仓储环境的任务调度过程做出以下假设：①起始点有多个，每台机器人从起始点出发，完成任务后返回起始点；②针对同批任务，每项任务只允许被1台机器人执行；③机器人的行驶速度是固定的，暂不考虑冲突情况；④任务的数量要远大于机器人的数量。

1.2 数学模型的建立

则所有机器人的总行驶距离的数学表达式为

式中：Xki为决策变量，表示第i 台机器人是否执行第k 个搬运任务。

式（5）表示所有配送任务将全部被分配，不存在某个任务不被执行；式（6）表示1 个目标点仅被1台机器人配送；式（7）为任务载荷约束，表示每台机器人可以执行的任务数量，Fi和ULi分别表示第i台机器人的实际任务载荷和载荷上限；式（8）为电量约束，表示每台机器人完成所有分配任务的剩余电量不能低于0，Ei为第i 台机器人的电量情况为第i 台机器人的单位距离电量消耗。

本文以机器人配送成本最小为目标，目标函数综合考虑机器人的配送运输成本、电量消耗成本和罚函数部分：

式中：λi为第i 台机器人单位距离运输成本；Pc为每台机器人的单位电量消耗系数；α1和α2分别为机器人的配送运输成本和电量消耗成本的权重系数，并且α1+α2＝1；ω 为罚函数的权重系数；Pe为罚函数，罚函数的构造思想是将有约束问题转化为无约束问题[9]，数学表达式为

2 混合遗传禁忌搜索算法

遗传算法（genetic algorithm，GA）是一种模拟自然进化过程的算法，该算法应用广泛，具备较强的全局择优能力，但也存在容易早熟、局部搜索能力较弱等缺点[10-11]。禁忌搜索算法（taboo search，TS）具有较好的局部搜索能力和记忆功能，但其搜索能力依赖于初始解的质量[12]。本文基于这2 种算法的优点，提出了混合遗传禁忌搜索算法（GATS）来解决多机器人的任务分配问题。先用遗传算法生成较优初始解，然后将此解作为禁忌搜索算法初始种群迭代寻优，这样不仅保持遗传算法全局寻优能力，同时增强局部搜索能力。混合遗传禁忌搜索算法流程如图2 所示。

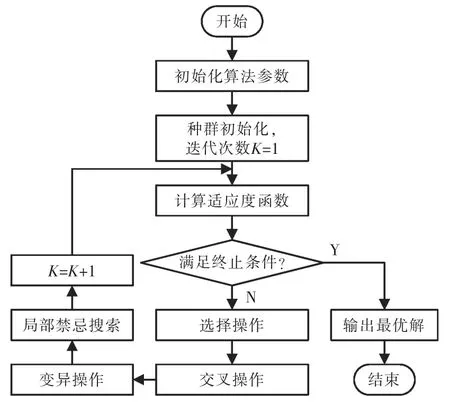
图2 混合遗传禁忌搜索算法流程Fig.2 Flow chart of hybrid genetic taboo search algorithm

2.1 遗传算法阶段

（1）编码。文中采用实数编码生成染色体，实数代表的数值就是任务编号。首先初始化染色体的长度N，再按机器人的数量M，把染色体分段，每台机器人都对应1 条染色体片段，再在相应染色体片段最前端和最末端加设起点位置，染色体片段中含有机器人起点、待接入任务点和执行顺序，如图3所示。

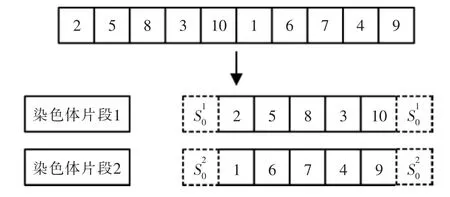
图3 染色体编码方式Fig.3 Chromosome encoding method

（2）产生初始种群。初始化种群，设定遗传算法中各初始参数，如种群规模、最大迭代次数、交叉与变异概率。

（3）计算适应值。取染色体中所有机器人完成全部任务的总成本的倒数作为适应度值，适应度函数定义为

（4）选择操作。首先按照轮盘赌规则筛选出一定份额的个体，然后用精英策略为后续种群进化挑选适应度值较高的个体。

（5）交叉操作。首先在染色体长度上随机选择2个数，使2 个数间染色体片段各自向另一染色体最前端迁移，再按顺序遍历2 条染色体，去掉重复基因，从而获得经过交叉的1 条新个体。

（6）变异操作。在染色体中随机抽取2 个位置基因，再在2 个基因间调换各基因位置次序，组成1个新个体。

2.2 禁忌搜索算法阶段

为加强遗传算法局部搜索能力，本文把禁忌搜索算法融合在遗传算法变异操作之后，通过引入禁忌表来避免反复迂回搜索，从而实现全局优化。主要步骤如下：

（1）获取初始解及初始化参数，选取经过遗传算法变异阶段的新种群，以适应度值最大的个体为禁忌搜索算法初始解，初始化禁忌表并设置禁忌长度参数；

（2）判断是否符合终止条件，如果符合条件则输出最优解并终止搜索，否则继续循环；

（3）根据当前解的领域映射模式，产生多个邻域解，并从中选出多个候选解，并计算各个候选解的适应值，保留较优的候选解进行后续判断；

（4）判断候选解是否符合藐视准则，若符合，则将其解禁出来，并作为当前最优解，同时将该解放入禁忌表，并更新禁忌表状态；若不符合，则筛选出候选解中未被禁忌的最优解为当前最优解，并更新禁忌表状态；

（5）当满足终止准则时，则停止搜索，输出最优解。

禁忌搜索算法流程如图4 所示。

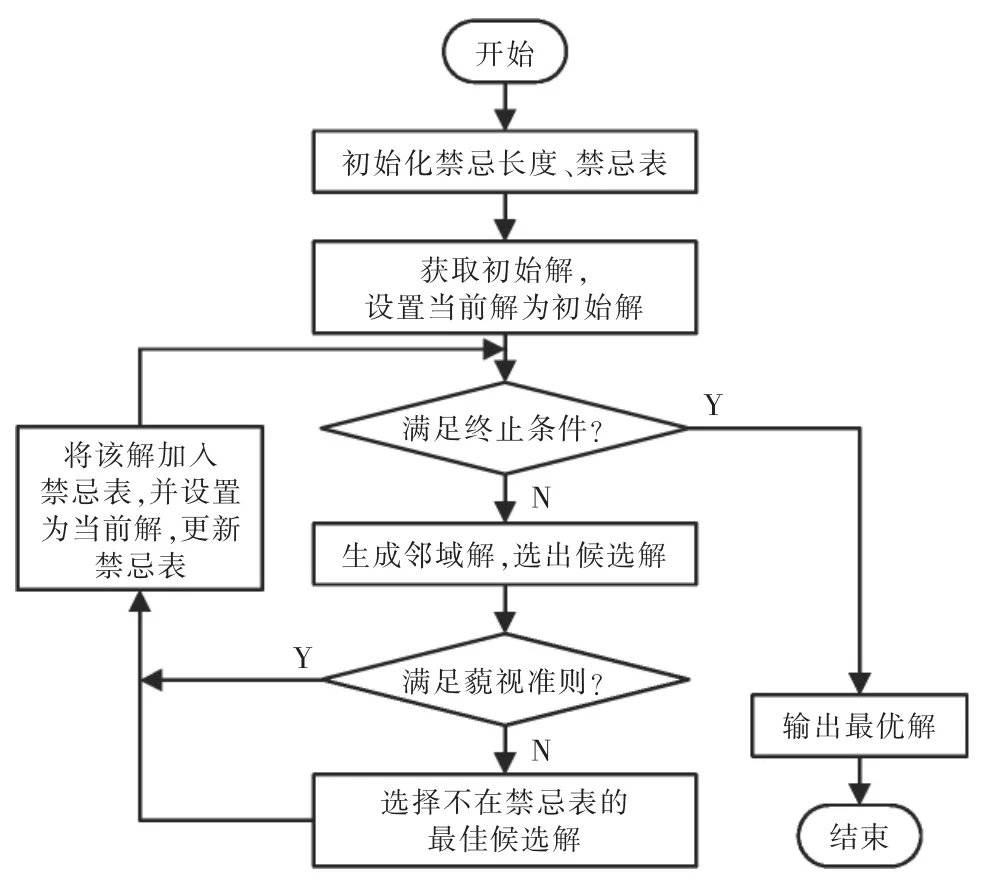
图4 禁忌搜索算法流程Fig.4 Flow chart of taboo search algorithm

3 仿真结果与分析

为验证所提算法的性能，本文在Windows10 操作系统上，使用Matlab2021b 软件对改进前后的算法进行仿真。假设仿真实验在100 m×100 m 的仓储环境中进行，用栅格法进行建模。仓储中有3 台机器人，30 个待分配任务，机器人的起始点互不相同，速度v 为1 m/s，每个机器人的任务载荷上限UL 为10。参数设置为Pc=0.5，权重系数α1＝0.6，α2＝0.4，ω＝100。将算法的种群规模定为100，迭代次数为500 次，交叉概率为0.9，变异概率为0.1。机器人部分性能参数如表1 所示。

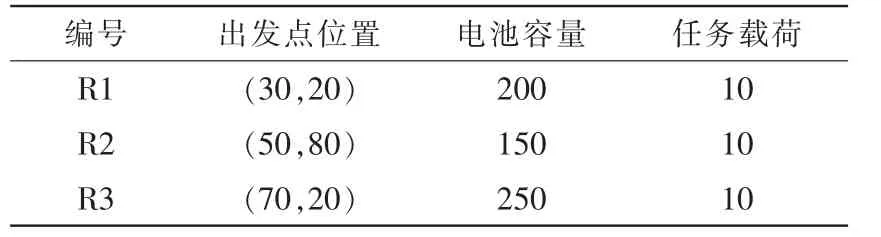
表1 机器人性能参数Tab.1 Robot performance parameters

通过上述参数对GATS、GA 和TS 算法的收敛速度和寻优能力进行仿真，如图5 所示。从图中可以看出，相比GA 和TS 算法，GATS 算法的目标函数值更低，表明GATS 算法在迭代过程中有利于跳出局部最优解，且其收敛速度也比GA 算法更快，验证了GATS 算法的有效性。

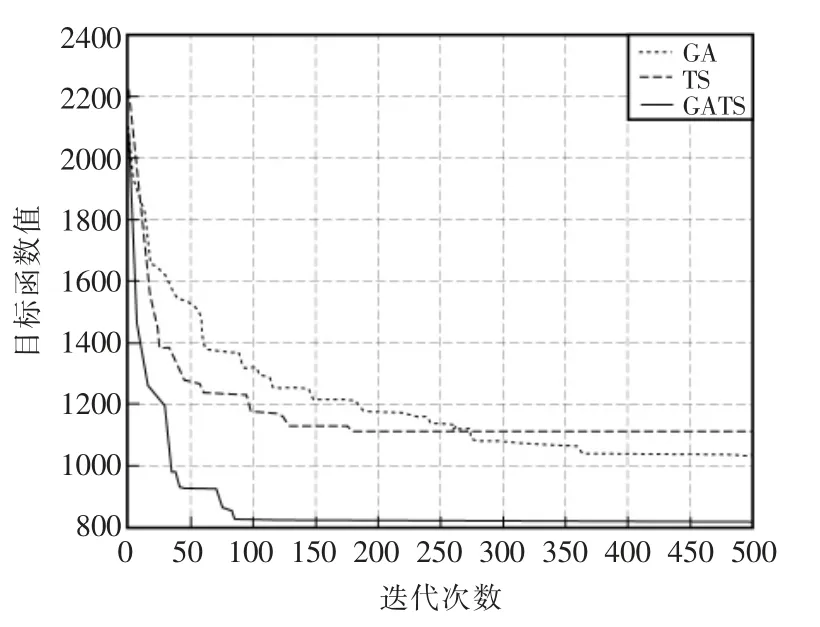
图5 三种算法的迭代图Fig.5 Iterative diagram of three algorithms

基于GATS 算法的多机器人任务分配仿真结果如图6 所示，任务分配优化结果如表2 所示，每个机器人都执行10 个任务，符合任务载荷约束条件。

表2 任务分配优化结果Tab.2 Optimization results of task allocation

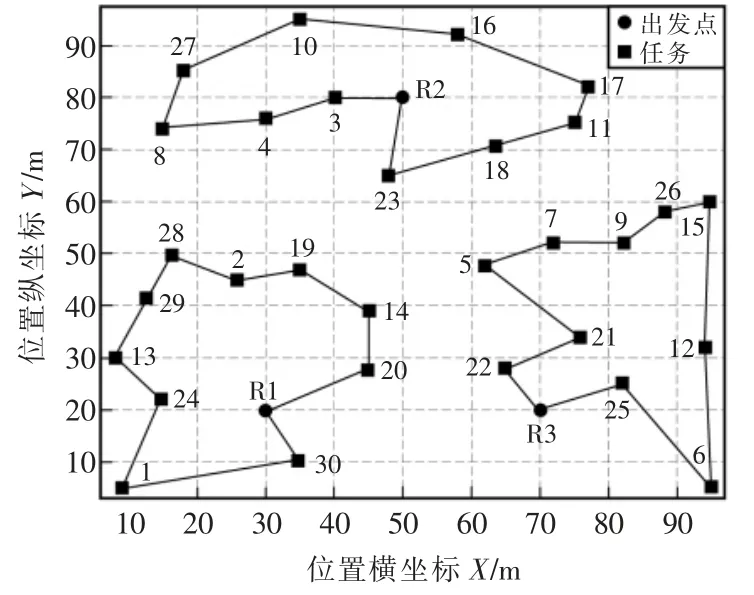
图6 多机器人任务分配优化结果Fig.6 Optimization results of multi-robot task assignment

为了进一步验证混合算法的寻优能力，本文设置机器人的数目分别为M=5，7，10，15，200，任务数量分别为N=50，70，100，150，200，终止迭代次数为2000 次，比较GATS、GA 和TS 算法的最优解。通过将每个实例在相同环境下分别运行10 次，记录10次运行结果中的平均值。表3 所示为各算法运行结果，从表3 中可以看出，本文所提算法的优化结果更接近最优解。

表3 不同算法优化结果对比Tab.3 Comparison of optimization results by different algorithms

4 结语

本文为解决仓储多机器人任务分配问题，首先建立一种多机器人任务分配模型；然后针对遗传算法易陷入局部最优且收敛速度较慢的问题，提出了一种混合遗传禁忌搜索算法；最后采用GATS 算法对不同规模的任务分配问题进行了仿真实验，并将其与GA 和TS 算法进行对比。仿真结果表明，混合遗传禁忌搜索算法能更好地解决多机器人任务分配问题。