小学数学教学“比较”运用研究

周建东

比较是通过将两类具有相同或相似属性的事物进行对比，进而分析事物的异同，认识规律。运用比较的方法，可以防止知识之间的相互干扰，把表面形式相似、容易彼此混淆的知识区分清楚，加深理解[1]。乌申斯基说过：“比较是一切理解和思维的基础”[2]。比较是数学学习的常用方式和手段之一，它能激起学生主动地、深入地、有质量地、有指向地研习，促进数学思维由表及里、由浅入深。数学教学中，教师要敏锐把握合适时机，引领学生展开比较，让学生在比较中辩明说清、辨析明义，把握本质、入脑入心。

一、在知识生长之处比较——发现联系，内驱引入

《义务教育数学课程标准（2022年版）》也指出，“要关注数学概念的现实背景，引导学生从数学概念、原理及法则之间的联系出发，建立起有意义的知识结构。”[3]教师要在知识生长之处引导学生适时比较，让学生在强烈的内心驱动下发现新旧知识存在的关联，自然绽放新知。如笔者在教学苏教版五年级上册“认识公顷”时，是这样来展开比较的：

知识点1：我们之前已经学习了一些面积单位，你能从小到大有序地说说吗？

生：……

知识点2：这些面积单位的大小是如何规定的？

生1：边长是1 厘米的正方形，面积是1 平方厘米；

生2：边长是1 分米的正方形，面积是1 平方分米；

生3：边长是1 米的正方形，面积是1 平方米。

知识点3：观察平方厘米、平方分米、平方米这三个面积单位，你发现了什么？

生4：面积单位通常都是以一个正方形的大小来规定的；

生5：面积单位跟正方形的边长有关，边长越大面积单位越大；

生6：正方形的长度都是10 倍的关系在变大；

生7：我发现，边长是多少长度的正方形，面积单位就是1 平方多少。

知识点4：你能根据刚才的发现，自己创造一些更大的面积单位吗？出示图1：

图1

边长是（ ）的正方形，面积是1（ ）。

学生通过比较，思维顿开，在1 平方米的基础上创造出了更大的面积单位：“边长是10 米的正方形，面积是1 平方十米”“边长是100 米的正方形，面积是1 平方百米”“边长是1000 米的正方形，面积是1 平方千米……”，此时，教师指出：“1 平方百米就是1 公顷，公顷就是今天要学习的新的面积单位。”

上述教学中，教师紧紧抓住知识生长之处让学生比较发现之间的脉络延展，让学生自己创造一些更大的面积单位，学生在强烈的学习欲望的驱动下，自然引入新知“公顷”。

二、在分层探究之后比较——揭示规律，建立模型

教师要在学生探究的各个环节适时引导学生比一比、想一想、说一说，让知识在比较中破茧而出。如教学苏教版三年级下册“求整体的几分之一”，笔者是这样来逐步深入组织学生展开比较的：

第一层次：改变数量之后的比较。探究“一篮蘑菇共6 个，1/3 是黑蘑菇，黑蘑菇有多少个？”，从“这篮蘑菇的1/3 是黑蘑菇”，想到把这篮蘑菇平均分成3 份，黑蘑菇就是1 份，由此产生用圆片代替蘑菇来分一分得到结果，或者用整数除法“6 ÷ 3”算出一份是几个的想法。接着把一篮蘑菇的个数改为9 个，求黑蘑菇的个数。教师在学生独立思考、实物操作、分数理解探究解决问题的基础上出示图2 和图3：

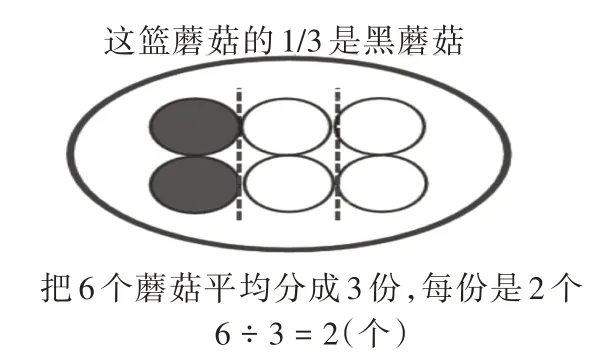
图2

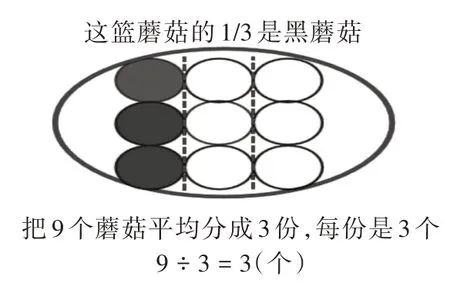
图3

同样是这篮蘑菇的1/3，为什么每份黑蘑菇的个数不相同呢？此时，学生的思维就聚焦到这篮蘑菇的总个数上，求黑蘑菇的个数也就是平均分为若干份后求每份是多少个，每份的个数与总个数有关。虽然两次都是求这篮蘑菇的1/3 是多少个，但由于组成整体的个数不同，所以整体的1/3 的个数不同。

第二层次：一份数的比较。此时，教师又出示图4 和图5：

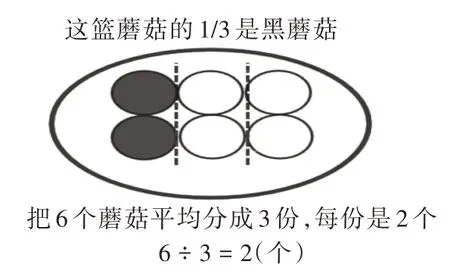
图4

图5

现在这篮蘑菇的总个数都是6 个，为什么每份黑蘑菇的个数不一样呢？学生的关注点自然而然就指向平均分的份数即题中的分数，虽然整体包含的蘑菇个数相同，但把整体平均分的份数不同，所以每份的个数就不同。

第三层次：整体比较。将上述解决的问题的过程同时用图6、图7、图8出示：

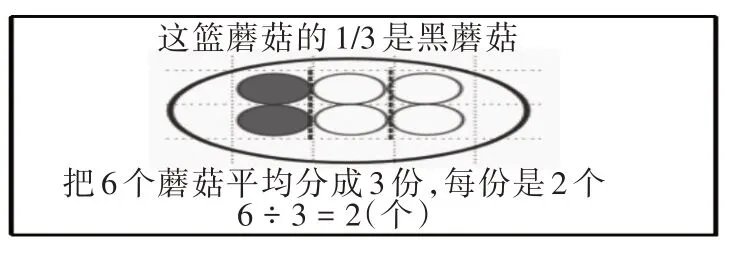
图6

图7

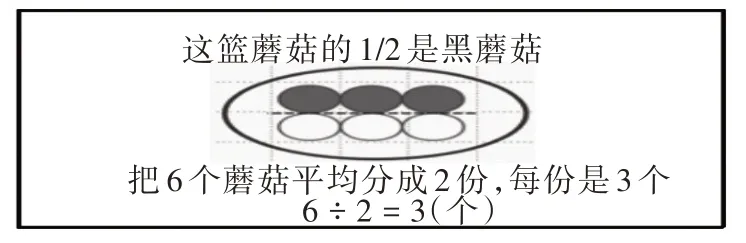
图8

图9

教师总结：都是求的什么？你有什么体会？学生在比较中概括得出了问题的共同点：都是求一个整体的几分之一是多少，体会到解决这类问题要抓住题中整体包含的数量和分数，关键是理解分数的意义，把整体的数量平均分成几份，数量关系也就显而易见了。

上述教学中，在分层探究之后，学生有目的、有针对性地进行了三次比较，在比较中发现求整体的几分之一的规律，主动而又深刻地建模，为后续求整体的几分之几打下坚实的基础。

三、在变式递进之中比较——体验过程，感悟深化

变式可以加强学生的数学技能和思维训练，引导学生发现“变”中“不变”的本质，同时还可以让学生探索“不变”中的“变”的规律，让学生在变式中触摸思维的脉搏[4]。如苏教版六年级上册“解决问题的策略”，在学生完成练习题“1 张桌子和4 把椅子的总价是2700 元，椅子的单价是桌子的1/5，桌子和椅子的单价各是多少？”后，抓住关键信息适时进行了两次变式比较：

变式一：“椅子的单价是桌子的1/5”还可以怎样说？（椅子与桌子价格的比是1∶5、桌子的价格是椅子的5 倍。）换成这些说法后，什么变了？什么没变？（表述两种量关系的形式变了，但假设的依据不变、假设后的数量也不变。）

变式二：“1 张桌子和4 把椅子的总价是2700 元”变式为“王叔叔带了3000 元，买了1 张桌子和4 把椅子后，还剩300 元”，怎么解决？“王叔叔带了2400 元去买1 张桌子和4 把椅子，还差300 元”，又该怎么解决？这样改编后，什么变了？什么没变？（总量没有变，数量关系不变。）上述变式比较中，紧扣假设的依据、假设的数量关系，将假设策略的运用不断向深处探寻。

教师要找准脉络、掐准“穴位”，在变式中即时组织学生展开深入比较，让学生在比较中明晰运用假设策略解决实际问题的题型结构，确定解题思路，感受假设的策略对于解决特定问题的价值，增强解决问题的策略意识，进一步发展分析、综合的推理能力。

四、在混淆出错之时比较——突出重点，指向本质

对一些相似或相近的数学知识，学生或是依葫芦画瓢照搬照用，或是审题不清分析草率，经常会出现混淆。教师要在学生混淆出错之时，指引学生采用多种方法进行比较，找到错误症结，规整思路，主动寻求正确的方法。如以苏教版六年级上册“列方程解稍复杂的百分数应用题”为例。笔者在教学中，有针对性地出示一组典型题“建造一座污水处理池实际投资比原计划节约10%，1.节约了4.8 万元，原计划投资多少万元？2.实际投资43.2 万元，原计划投资多少万元？3.建造一座污水处理池实际投资是原计划的90%，实际节约了4.8 万元，原计划投资多少万元？”让学生自主解答。在反馈交流中，对第一小题用“解：设原计划投资x 元。x- 10%x= 4.8”。错误方法解答的学生人数果然不少。此时，笔者让学生先将两小题仔细比较，再将第一和第三小题比较，可以读一读、圈一圈、画一画、说一说等，从题目本身和解题思路两方面比较之后再来辨析下定论。学生用自己的方法进行了两次细致地比较，发现错误的症结在于没有抓住题中的已知量理解意思，并根据题意从已知量出发分析等量关系，已知量表示的意思相同，但等量关系不一定相同。教师在学生比较交流反馈之时，相机出示图示，从理解题意、画线段图、分析等量关系等方面比较。

上述教学中，教师着力于混淆出错处浓墨重彩引导学生用多种方法比较，在比较中突出重点，化解难点，条分缕析、明白透彻，指向本质、提升思维[3]。

五、在思维定式之际比较——丰富提升，融会贯通

在学生的学习中，知识迁移是一种重要的学习方法[4]。但也因为新旧知识的迁移，学生容易产生思维定式，对学习新知识产生零迁移甚至是负迁移，造成新盲点。如果没有厘清这些新盲点，学生容易对新知识，甚至是对原本的旧知识产生模棱两可的认知。此时，教师如能在知识的新盲点上巧用比较策略，通过对比帮助学生扫清知识的盲点，将有助于他们建立起清晰的知识体系，为提高思维的灵活性奠定扎实的基础[5]。

如在教学苏教版六年级上册“比例尺”时，例题及随后练习呈现的均是缩小比例尺，易于使学生造成思维定式，简单地认为，所有比例尺化简后的前项都为“1”。于是在学完缩小比例尺后，笔者出示了“一个精密零件长2 毫米，把它绘在图纸上长10 厘米，求这幅图的比例尺”一题。绝大部分学生认为结果是1∶50。笔者以错误结果为资源，让学生说说对1：50 的理解：“图上1 厘米，表示实际50 厘米；图上距离是实际距离的1/50；实际距离是图上距离的50 倍。”笔者追问：“这个比例尺符合实际情况吗？题中的图上距离与实际距离比较哪个大呢？它是图形的缩小还是放大呢？”而后，再让学生结合比例尺的意义去审题、去理解：题中的图上距离应是实际距离的50 倍，原来是受缩小比例尺的思维定式影响，习惯性地认为比例尺的前项通常为1，混淆、颠倒了题中的图上距离和实际距离，本题是一个放大比例尺，结果应为50∶1。至此，再让学生深入比较两种比例尺的联系和区别，在追根究底中使学生理解到都是根据比例尺的意义——用图上距离∶实际距离，关键是要正确审题，搞清题中的图上距离和实际距离；同时，它们又有区别：缩小比例尺的比值都小于“1”，而放大比例尺的比值都大于“1”。

学生在比较中巧妙地化解了思维定式的负迁移，有效地提升了思维层次，深刻地把握了知识的实质。

六、在回顾反思之间比较——完备建构，优化思路

教师要引导学生在回顾反思中比较，可以把相同的知识点放在一起进行比较，那么就可以更好地激发学生的数学前经验，唤醒以前的知识结构，并把新的知识结构融入旧的知识结构之中，形成一种全新的完备知识结构。如笔者在教学苏教版六年级上册“解决问题的策略”时，在引入、揭示和感受假设策略之后，引导学生在两个层次的回顾反思中比较。

第一层次：回顾例题的解题过程，是怎样假设的？这些假设具有什么共同特征？假设在解决这道例题时起到什么作用？让学生初步体会到假设是解决问题的一种策略。

第二层次：回顾以往的数学学习，曾运用假设的策略解决过哪些问题？

生1：计算除数是两位数的除法，把除数当作整十数试商；

生2：估算时把接近整百或整十的数看作整百数或整十数，估算出大致的结果；

生3：已知两个数的和与差，假设两个数同样多，分别求出这两个数；

生4：在列方程解决实际问题时，设未知数时用到了假设策略；

……

教师引导比较：“这些运用假设的策略解决问题的过程有什么共同点？”“假设策略对解决这些特定问题具有什么价值？”“以后再遇到一个复杂或者陌生问题时，你会怎样想呢？”学生在比较中直指学习目标，发现假设策略是一种重要且常用的解决问题的策略，可以运用在不同的地方，假设策略的表现形式灵活多样，既可以用图形来表达，也能用线段表达，还能在计算中表达。这些解决问题的过程，实际上都是通过假设把复杂问题转化为简单问题的过程。

学生在两个层次的回顾反思比较中，充分体验和感受了假设策略的价值，增进了策略运用意识，丰富完备了假设策略的建构，优化了解决问题的思路，提升了思维力和学习力。

数学会因为比较而深刻，因为比较而丰富。比较是推动学生的数学学习走向实质、走向深入、走向智慧的方法[6]。总之，在课堂教学中，教师要善于捕捉良机，引导鼓励学生学会比较、主动比较、善于比较，在比较中学习，在比较中提升。