弯管入流对离心泵固液两相内部流动特性研究

姚杭志，宋文武，由丽华，吕世杰

（1.西华大学能源与动力工程学院，四川 成都 610039；2.四川省紫坪铺开发有限责任公司，四川 成都 610091）

0 引言

离心泵作为广泛应用于各个领域的流体机械，为了达到设计要求通常采用直管（均匀）入流的方式使流体沿入口段稳定进入叶轮。但其在工程应用中，由于安装布置的要求、空间局限性以及环境等影响因素，进口段需要采用弯管而非直管的非均匀入流方式。

目前，国内外学者已针对弯管（非均匀）入流进行了相关研究，其主要研究领域集中在压缩机扩压器。KIM［1］为了比较具有两种不同进气口结构的离心压缩机性能，通过实验研究直管和喷嘴形状为90度的弯管。结果表明，两种不同进气口配置之间的压缩机性能存在显着差异，并详细说明来自弯曲进气口配置压缩机的性能行为。MA［2］等为了研究具有均匀和非均匀间隙压缩机级联通道出口处流场的影响，提出了一种径向不均匀的尖端间隙并进行实验研究。结果表明，不均匀的尖端间隙会减少叶片流动通道中的低能量流体，也会削弱尖端区域的二次损耗和流动阻塞。赵正［3］等采用CFD 数值仿真的方法，基于均匀和非均匀条件下直叶扩压器中入口角对流动影响的比较研究，分析入口角向非均匀性扩展对扩压器流动机制的影响，并探究扭曲形叶片与入流角扩展朝向非均匀的适配能力。

随着CFD 技术的不断发展和进步，众多学者热衷于通过数值模拟的方法将研究非均匀流动的重心转向泵类产品，例如：核主泵、轴流泵和双吸离心泵等。施卫东［4］等为了对比研究两种不同入流条件对轴流泵性能的影响，建立了两种类型的非均匀速度入口分布并进行数值计算。结果表明，适当控制非均匀入流情况可使其性能优于轴向均匀入流。乔翼飞［5］研究了进口流场畸变对反应堆冷却剂循环泵（核主泵）内部压力脉动和振动特性，分析结果表明，非均匀来流下的核主泵内各个过流部件水力性能都有所下降，压力脉动的变化会导致振动最大值变化。同样李双［6］采用比较不同入流的方法分析双吸离心泵的内部压力脉动特性，构建了水平和竖直两种弯管作为非均匀入流方式。研究结果表明，非均匀入流对双吸离心泵的效率扬程影响较大，其次竖直与水平入流对泵的性能影响逐渐变大。靳恩［7］针对不同入流条件对离心泵的内部流动影响进行研究，得到的结果为随着弯管角度增大和直管角度减小离心泵的压力脉动明显增大，且在小流量工况下影响更大。

在实际生活和工作实践中往往采用固液两相流作为离心泵运行工作介质，因此近年来有许多学者逐步对各领域流体机械结合固液两相流做了深入研究。目前在两相流动的数值理论方法的基础上，得到了三种较为成功的多相流模型分别为Mixture 模型、离散相模型（DPM）和离散元模型（DEM）。首先ZHANG 等［8］运用Mixture 模型和RNGk-ε湍流模型结合对低比转速离心泵固液两相流进行数值模拟分析，结果表明，固相颗粒的直径和浓度对泵性能影响较大，随着颗粒浓度的增大隔舌附近流动紊乱现象以及叶片吸力面磨损情况均愈发明显。HUANG 等［9］为了研究单级离心泵固液两相流在瞬态的变化情况，采用离散元模型（DEM）-CFD 耦合对三维瞬态过程进行了数值模拟。研究结果表明，在启动阶段，进入泵内的颗粒大于同期排出的颗粒并且均匀分布在流道入口处。JIANG［10］等采用双向耦合离散相模型（DPM）方法研究了渣浆泵固液两相流动特性和磨损形式。并在数值计算和实验结果较好吻合的条件下得出内部流场磨损程度与体积流量和固体体积分数呈正相关；但叶轮入口处的磨损程度与粒径呈负相关。

综上所述，当前弯管入流对离心泵进行的相关研究仅是在单一的清水介质条件下［11-14］，而固液两相离心泵的入流方式也仅是直管入流［15，16］，目前尚未见针对弯管入流对离心泵固液两相内部流动特性的研究文献报道［17-21］。因此，本文采用Mixture多相流模型对弯管入流角度θ为0°、45°、60°的离心泵模型在设计工况和偏工况下进行数值模拟，并且将清水介质改为固液两相介质，在设计工况下分析不同弯管入流角度对离心泵固液两相内部流动特性的影响，为以后的离心泵弯管入流设计过程提供具有一定的理论依据。

1 计算模型和方法

1.1 计算模型

本文所研究的离心泵设计参数分别为额定流量Qd=243 m3/h，扬程H=18 m，额定转速n=1 450 r/min，叶轮的进口直径D1=162 mm，叶轮的出口直径D2=262 mm，比转速ns=157，叶片数Z=6。

本文首先通过商业软件UG 构建离心泵三维模型，并且在蜗壳出口处添加5倍叶轮直径的出口段，再采用ICEM软件对该模型进行网格划分，使流体介质进入离心泵能充分流动且不产生回流现象，为获得更加精确的结果，分别对三种角度的进口段和出口段进行六面体结构化网格划分，对叶轮和蜗壳采用适应性较好的四面体非结构网格且质量均大于0.3，离心泵模型网格如图1所示。

图1 离心泵模型网格Fig.1 Centrifugal pump model mesh

1.2 网格无关性分析

在液相条件（清水）下，以入流角度θ=0°，额定流量Qd=243 m3/h，采用5 种不同网格数方案进行定常数值模拟计算，探究网格数量对离心泵流场的影响如图2所示。随着网格数量的增加，其效率呈先增大后趋于稳定的趋势，当网格数达到3.8×106之后计算趋于稳定，最后确定3 种不同模型的网格数方案如表2所示。

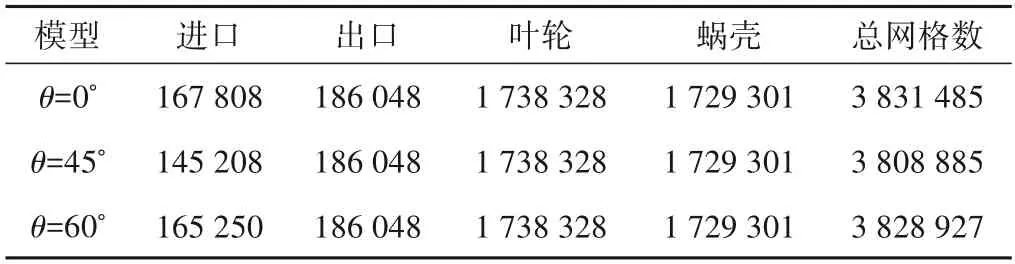
表2 3种模型网格数量方案Tab.2 Three model mesh number schemes

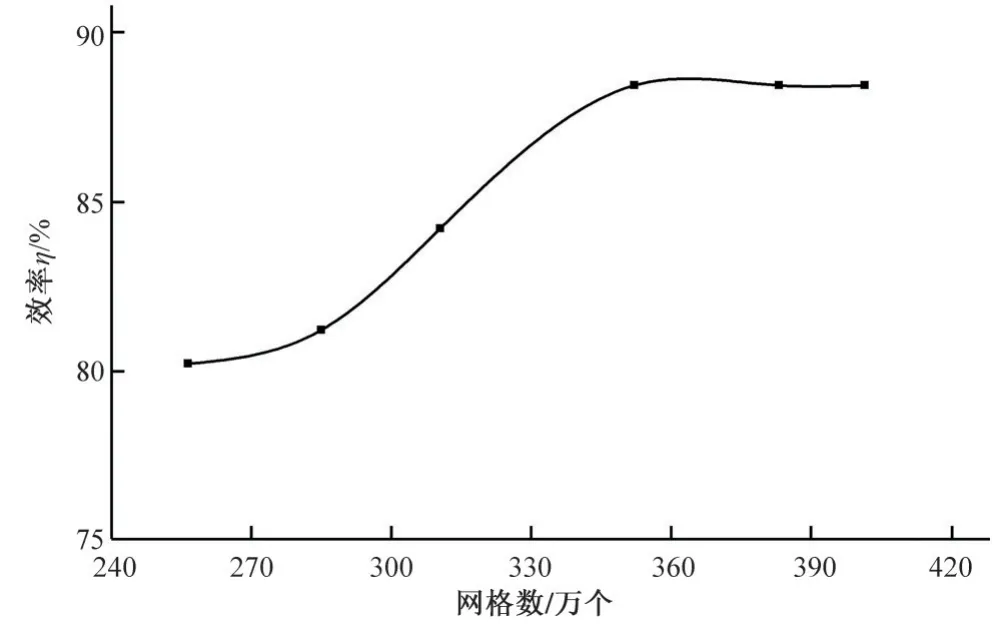
图2 网格无关性验证Fig.2 Grid independence verification

1.3 监测点布置及进口截面的确定

为了研究离心泵内部固液两相流动特性需在叶轮内部各重要位置布置监测点。如图3所示，在离心泵模型的叶轮流道内两相邻叶片间由靠近吸力面向下一叶片的压力面逐渐靠近处依次设置监测点M1～M3，隔舌位置处设置监测点G1，以研究3种离心泵模型在额定工况下内部压力脉动和径向力的变化。

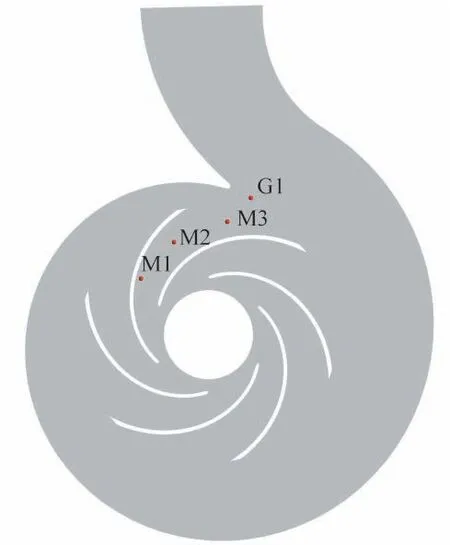
图3 监测点的布置Fig.3 Layout of monitoring points

如图4所示，在离心泵进口段设置进口截面分别为S1、S2、S3，以研究固体颗粒随着入口角度地改变其压强与速度的不均匀度变化情况。

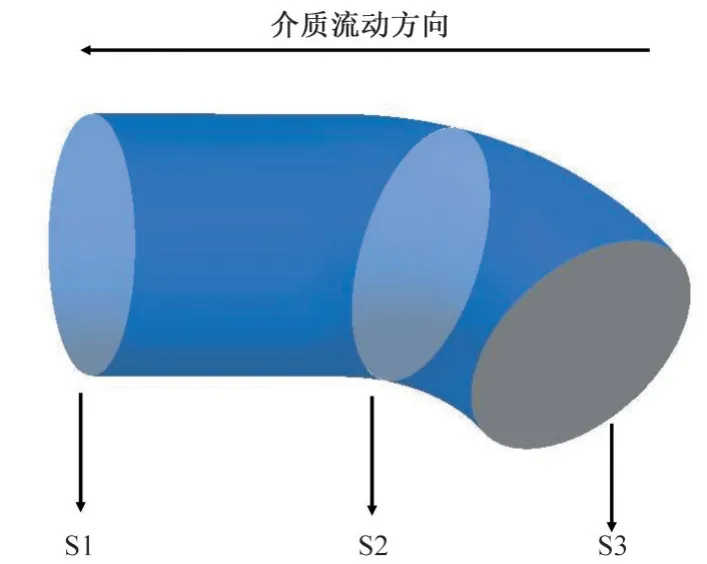
图4 进口截面的确定Fig.4 Determination of the inlet section

1.4 数值计算方法

Mixture 多相流模型将固液两相间作为互相穿插的连续介质，适用于各相不同速度或相同速度的两相流，故本文通过ANSYS 商业软件，对于固体颗粒相，采用Mixture 多相流模型，对连续流体相，采用标准k-ε湍流模型。

连续方程为：

动量方程为：

第二相的体积分数方程为：

漂移速度方程为：

1.5 边界条件的设置

在CFX 前处理对离心泵模型进行边界条件设置，选择无滑移边界条件，进口边界条件为总压，出口边界条件为质量流；在各交界面处分别设置Frozen Rotor和General Connection，设置模型定常计算步数为2 000 步，计算步数内收敛于10-5达到收敛要求。在进行非定常计算时，设置计算总时间为t=0.206 9 s，时间步长为Δt=1.149 4×10-4s，即计算叶轮旋转5 圈，每一步长叶轮转过1°，含沙水条件为98%的清水和2%浓度的固体颗粒，颗粒粒径为0.1 mm。

2 计算结果分析

2.1 离心泵外特性分析

2.1.1 清水条件下离心泵外特性分析

在清水条件下，在各流量工况下3 种入流角度对离心泵外特性的影响，如图5所示。不同入流角度对离心泵外特性的影响规律基本一致，扬程和效率均下降。随着流量的增大离心泵扬程呈现一直下降的趋势并且下降幅度逐渐递增，效率呈现先增大后减小的趋势并且在设计工况时达到最大值，扬程和效率均在最小流量工况0.6Qd时差距最为明显，当入流角度θ=45°时，在小流量工况0.6Qd处效率下降最大为1.49%，在大流量工况1.2Qd处效率下降最小为0.047%；当入流角度θ=60°时，同样也在小流量工况0.6Qd处效率下降最大为2.35%，在设计工况下效率下降最小为0.127%。这是由于在偏工况条件下，随着入流角度的增大改变了离心泵水流冲角，增大叶顶冲击损失，使离心泵在入口位置更容易产生预旋等现象，从而影响其外特性性能。

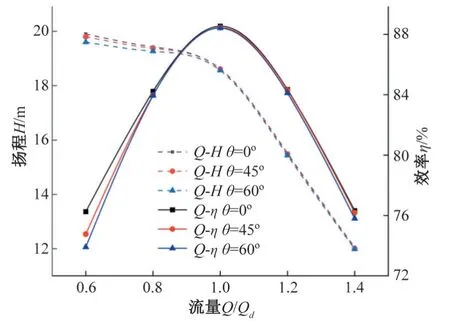
图5 清水条件下外特性仿真值曲线Fig.5 Simulation value curve of external characteristics under clear water condition

2.1.2 固液两相条件下离心泵外特性分析

固液两相条件下离心泵的外特性变化曲线如图6所示。以固液两相作为介质的弯管入流对离心泵的外特性影响规律并不一致，扬程呈现接近线性的下降规律，效率呈现逐渐下降的趋势并且均在最小流量工况下达到最大值，扬程和效率均在最大流量工况1.4Qd时差距最为明显。当入流角度θ=45°时，在大流量工况1.4Qd处效率下降最大为6.03%；当入流角度θ=60°时，同样也在大流量工况1.4Qd处效率下降最大为11.26%。在固液两相的最大流量工况1.4Qd下，随着入流角度的增大，入流角度θ=45°到θ=60°两者间效率减小幅度近乎入流角度θ=0°到θ=45°两者间的200%，这是由于固体颗粒随着流量工况的增大而增多，并随着入流角度的增大，两者协同作用的影响下导致离心泵进口冲水角改变，叶轮内部流道受阻，叶轮内流动紊乱不均匀，能量耗散增多，进而导致水力损失变大，效率大幅度下降。

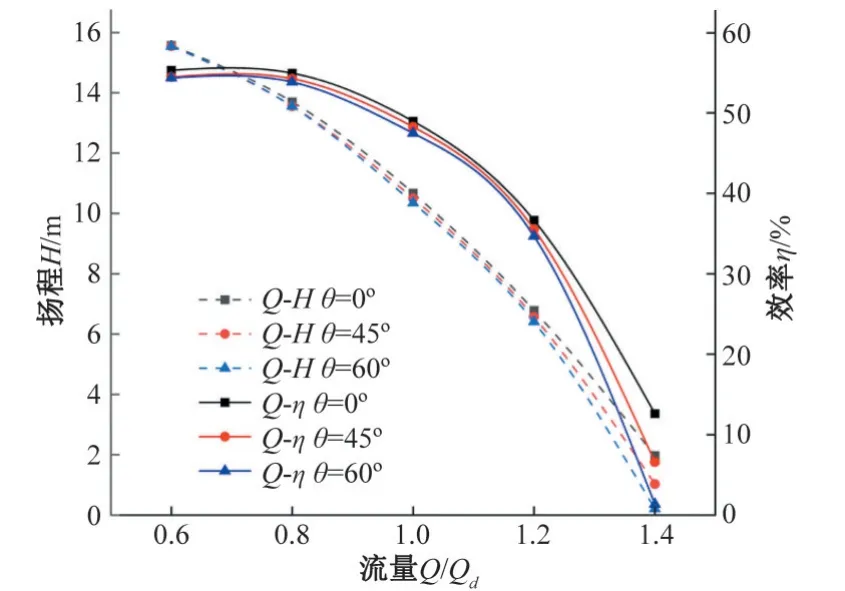
图6 固液两相条件下外特性仿真值曲线Fig.6 Simulation value curve of external characteristics under solid-liquid two-phase condition

2.2 进口段各截面不均匀度分析

为了进一步研究固液两相离心泵内流动现象，首先选取S1、S2 和S3 的进口截面分析进口段内固体颗粒流动特性，下文所分析研究的工况为标准工况1.0Qd。

为了详细阐明弯管所导致的不均匀入流对叶轮进口表明静压分布的规律，引入压力脉动系数Cp为压力脉动强度，压力脉动系数［22］定义为：

式中：p为瞬间压力值，Pa；为平均压力值，Pa；u2为叶轮出口的圆周速度，m/s。

为了定量的阐述弯管对进口段均匀化的影响，定义截面轴向速度与平均速度之差的均方差为不均匀度，表征流速的均匀性，利用两种变量的均方差来描述流动的不均匀性，当不均匀度等于0为均匀入流，不均匀度σk定义［23］为：

式中：xi为轴向速度（轴向压力），m/s（Pa）；xa为平均速度（平均压力），m/s（Pa）。

图7为不同弯管入流条件下进口各截面的压力和速度不均匀度曲线。由图可知，直管入流时，随着截面由入口向叶轮方向移动，压力和速度不均匀度总体呈现不断增大的趋势，尤其是压力不均匀度在靠近叶轮入口截面明显增加；45°和60°入流时，压力和速度标准差先增大后减小，在转弯处截面S2 的标准差值达到最大，均匀性最差；随着弯管角度的增大，标准差幅值也明显增大，说明弯管入流对进口管的压力和速度存在影响，并随入流角度的增大而影响加剧。

图7 进口段截面不均匀度曲线Fig.7 Inlet section unevenness curve

2.3 叶轮内部静压和固体颗粒分布

2.3.1 叶轮内部静压分析

不同入流角度对离心泵叶轮静压分布如图8所示，3 种入流角度离心泵叶轮流道的静压分布规律基本一致，都是从叶轮进口到蜗壳进口，叶轮流道静压分布随着径向圆周的增大而增大，在叶片吸力面顶部均匀分布6 个小于-1.0×10-4Pa 的低压区，即叶轮进口压力最低。随着入流角度的增大，叶片吸力面顶部的低压区范围呈现先减小后增大，当入流角度θ=45°时的低压区范围最小，θ=60°时的低压区范围最大，但低压区个数无变化。其原因是入流角度的增大，加剧含有固体颗粒的清水介质的不稳定流动，使叶片表面受力不均匀。

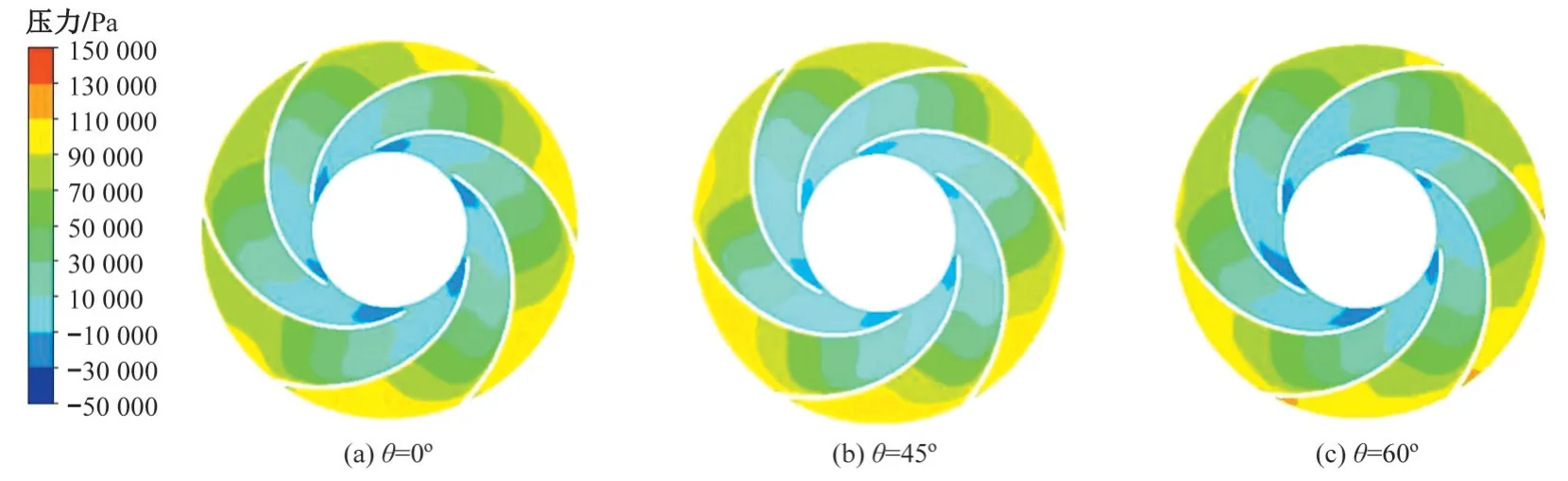
图8 叶轮内静压分布Fig.8 Static pressure distribution in the impeller

2.3.2 叶轮内固体颗粒分析

固相体积分数表示固体颗粒所存在的区域并表明此区域位置的磨损程度。图9 为3 种入流角度θ=0°、45°、60°的叶轮内固相体积分数，由图可知，3种入流角度下流道内固体颗粒主要由离心泵叶轮旋转而带动，使固体颗粒的分布情况产生较大变化，大部分堆积在叶片吸力面尾部，另有少量固体颗粒分布在各流道内部，从叶轮进口到叶片的1/2 处基本无固体颗粒的附着与磨损。随着入流角度的增大，叶片吸力面尾部上的固体颗粒浓度逐渐升高，固相体积分数沿周向向着流道扩散呈先减小后增大的趋势。此现象是因为随着入流角度的增大，叶片吸力面压力较叶片压力面压力减小幅度加剧，流体速度加快，所以叶片吸力面上的固体颗粒逐渐向着尾部堆积。即此离心泵叶片的吸力面尾部是受固体颗粒磨损最严重的位置。

图9 各入流角度下叶轮内固相体积分数Fig.9 Volume fraction of solid phase in the impeller at each inlet angle

2.4 压力脉动特性分析

2.4.1 叶轮流道以及隔舌监测点时域图分析

图10 表示3 种入流角度下离心泵叶轮流道内监测点M1～M3以及蜗壳隔舌G1的压力脉动时域图，如图所示，各监测点的压力脉动在3 种入流角度下呈现基本相同的变化规律，均随时间呈周期性变化。

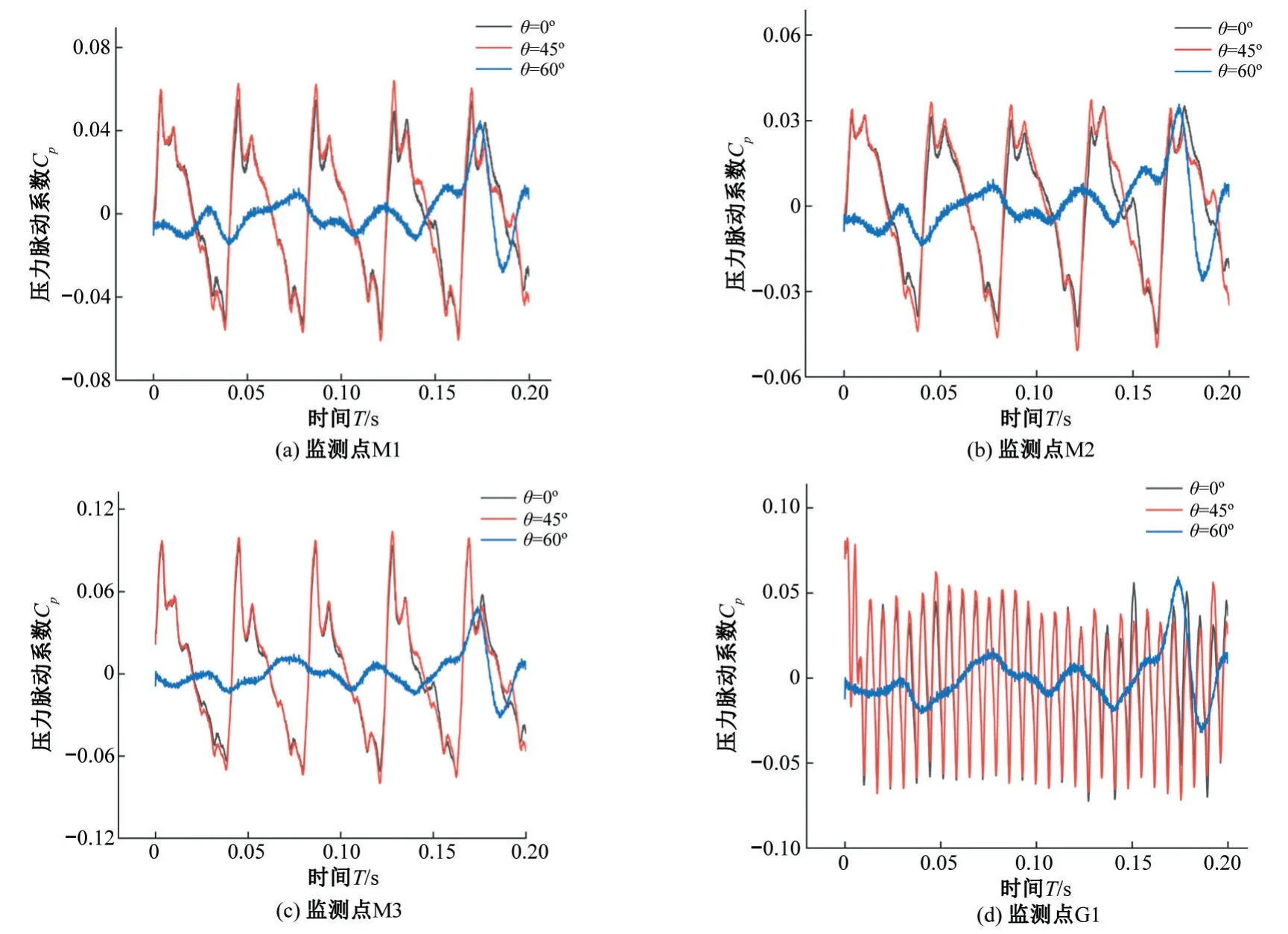
图10 不同入流角度监测点压力脉动时域图Fig.10 Pressure pulsation at monitoring points of different inlet angles

首先观察叶轮流道内监测点的情况可知，由进口到出口的压力脉动幅值根据时间的变化表现出周期性并且逐渐增大。随着入口角的增大，各监测点的压力脉动系数的幅值先减小后增大，在监测点M2 处，入流角度为θ=45°的压力脉动幅值略大于θ=0°。总体上看，当入流角度θ=60°的各监测点压力脉动幅值均小于θ=0°和θ=45°，说明在固液两相条件下，对入流角度θ=60°的叶轮流道压力脉动影响较小，但对叶轮出口附近的压力脉动影响较大，这是由于叶轮出口与蜗壳进口存在动静干涉的影响，是叶轮出口附近的压力脉动波形发生紊乱，从而导致叶轮出口附近的压力脉动幅值增大。

其次观察蜗壳隔舌位置的监测点，发现监测点G1 压力脉动随时间的变化幅度较大，随着入流角度的增大，隔舌位置所受压力脉动影响依次递减。

2.4.2 叶轮流道以及隔舌监测点频域图分析

本文的高比转速离心泵转速n=1 450 r/min，叶片数Z=6，故转频fr=1 450/60=24.17 Hz，fn=6fr=145 Hz。通过傅里叶变换（FFT）转化后得到如图11所示的不同入流角度监测点压力脉动强度频域图。

图11 不同入流角度监测点压力脉动频域图Fig.11 Pressure pulsation at different inlet angles

由图11所知，叶轮流道内监测点M1到M3的压力脉动波动范围主要集中在1 倍叶频（145 Hz）内，而隔舌位置监测点G1 的压力脉动波动范围则主要集中在3倍叶频（446 Hz）内。其次叶轮流道内监测点的压力脉动幅值在1 倍转频时表现的最为突出，在二倍以及其他倍数转频下也发现了峰值，而隔舌位置监测点的压力脉动最大峰值是出现在1 倍叶频时，其余相对峰值出现在二倍以及其他倍数叶频下。说明叶轮流道由进口到出口，监测点M1 到M3 的压力脉动逐渐增大，但随着入流角度的增大压力脉动幅值先增大后减小。

当固体颗粒浓度Cv=1%，颗粒直径为0.2 mm，入流角度θ=0°时，监测点M1～M3 的压力脉动强度幅值在24 Hz 达到最高，分别为0.036 4、0.027 2、0.05 0，监测点G1 的压力脉动幅值在145 Hz 达到最大0.042。入流角度θ=45°时，监测点M1～M3 的压力脉动幅值同样在24 Hz 达到最高，分别为34.839、26.874、47.413，监测点G1 的压力脉动幅值在145 Hz 达到最大39.174。但入流角度θ=60°时，压力脉动出现明显的减小，监测点M1～M3的压力脉动幅值却在1/2 转频达到最高，分别为6.920、4.867、6.521，监测点G1 的压力脉动幅值也在1/2 转频处达到最大8.626。这是由于入流角度过大，导致固体颗粒随着叶轮转动过程中逐步吸附在叶片吸力面尾部，使流道不再发生幅度的流动紊乱，所以压力脉动波动才会减弱。

2.5 径向力分析

图12、图13 为不同入流角度下离心泵的叶轮和隔舌径向力的分布情况，由图可知，只有入流角度θ=0°和45°时径向力分布呈和叶片数相等的六边形分布，θ=60°时径向力比较平稳变化范围不大。随着入流角度的增大叶轮的径向力呈先增大后减小，当θ=45°的径向力变化范围最大，最大值为260.4 N；随着入流角度的增大隔舌处的径向力呈先减小后增大，在θ=60°的径向力达到最大值为113.56 N。说明在同一浓度的固体颗粒介质条件下，改变入流角度对叶轮以及隔舌位置的径向力影响较大。并且叶轮径向力影响规律与叶轮流道内压力脉动强度规律相似，均在θ=45°时产生驼峰。

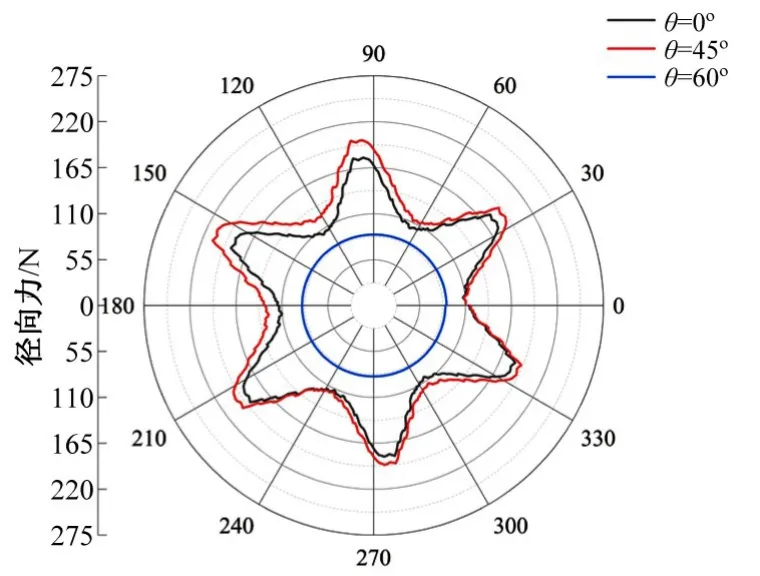
图12 叶轮径向力分布Fig.12 Radial force distribution of the impeller

图13 隔舌径向力分布Fig.13 Radial force distribution of the tongue

3 结论

离心泵性能随入流条件的变化而改变，特别是在两相流动条件下，入流方式使得固液入流已不在均匀的条件下，本文研究的结论如下。

（1）在液相和固液两相条件下，离心泵的扬程和效率均随着入流角度的增大而有一定的减小，但清水条件下，在小流量工况0.6Qd时影响幅度最大，在固液两相条件下，在大流量工况1.4Qd影响幅度最大。

（2）在固液两相条件下，叶片吸力面尾部受磨损影响最大，当入流角度θ=60°时，该位置的固体颗浓度最高。

（3）在固液两相条件下，随着入流角度的增大叶轮内部压力脉动幅值先增大后减小，说明入流角度与含固体颗粒的工作介质二者协同条件下对离心泵内部影响较大。

（4）在含同一浓度的固体颗粒介质以及入流角度改变的情况下，离心泵径向力有大幅度变化，即随着角度的增大叶轮径向力先增大后减小，隔舌径向力则相反。