基于多目标混合蛙跳差分进化算法的皂市水库优化调度
杨丽娟,薛联青,2,伍佑伦,盛 东,刘远洪,李 娜,周天文,何怀光
(1.河海大学水文水资源学院,江苏 南京 210098;2.皖江工学院水利工程学院,安徽 马鞍山 243031;3.湖南省水利水电科学研究院,湖南 长沙 410114)
0 引言
水库运行的多目标问题一般包括模型构建、优化求解和方案选择三部分[1]。在模型构建方面,围绕水库防洪、发电、供水、生态等效益的多目标调度研究逐渐增多,取得了较多有意义的成果,例如陈悦云等[2]面向赣江流域的发电、供水、生态要求,建立流域水库群优化调度模型,分析得到典型方案下三目标的竞争关系;YU等[3]建立了基于多目标博弈论的三峡水库多目标优化模型,求解三峡水库经济、社会和生态效益的平衡问题。
优化算法作为求解水库多目标调度问题的必要手段,目前主要有传统算法和现代智能算法,传统算法以线性规划、非线性规划、动态规划等为主,例如李想等[4]采用二次规划、混合整数线性规划和非线性规划3 个模型对比求解某水库的供水、发电调度问题。现代智能优化算法的应用目前更为广泛,如遗传算法、粒子群算法、差分进化算法等[5-7],在水库多目标优化求解中取得了较好的效果;方国华等[8]在蛙跳算法的基础上,采用混沌理论初始解生成、动态更新外部档案集与自适应差分局部搜索等策略,提出改进后的多目标混合蛙跳差分算法,在水库多目标调度模型求解过程中具有较好的寻优性能。
通过优化算法求解后,会得到一系列方案解,而不是单一的最优解,因此需要根据决策者的要求选择最符合水库运行情况的决策方案,目前应用最广泛的方法包括层次分析法、熵权法、逼近理想点法等,文晓彤等[9]以发电等4个指标的综合增加值最大为原则,在非劣决策方案集中优选得到了水库长期优化调度的均衡方案。
以皂市水库为研究对象,建立以发电、供水和生态为目标的优化调度模型,采用多目标混合蛙跳差分进化算法进行模型求解,并利用AHP-TOPSIS 的主客观组合赋权法优选多目标方案,研究成果可以提高皂市水库的社会效益、发电效益及生态效益,为其进一步科学调度提供依据。
二是定期召开联席会议,深化拓展联动执法。组织太湖流域江苏、浙江、上海两省一市水行政主管部门召开专项执法联席会议,《太湖流域管理条例》贯彻实施监督检查座谈会、推进会及案件处理等各类专题会议,分别与江苏、浙江水行政执法队伍合作开展了地方性法规规章与《太湖流域管理条例》适应性分析、太湖流域(江苏省)“一湖两河”联合巡查制度后评估等重点河湖及省际边界等特殊问题专项研究,总结经验和成效,不断深化执法合作,营造流域团结治水的良好氛围。同时将联合巡查制度向省际边界地区拓展,与苏州、嘉兴、青浦支队签订了联动执法及联席会议制度,为相关区县搭建了平台,建立起沟通协调机制。
从1978年到2018年,中国改革开放已走过四十个年头。四十年来,随着经济高速发展,中国社会组织的发展也进入了快车道。社会组织数量的快速增长、社会组织活动领域不断扩展,社会组织的贡献和作用已引起党和人民的高度关注,党的十九大报告对社会组织赋予了极高的政治地位:社会组织成为新时代民主协商制度的重要类别;社会组织与“产业工人、青年农民、高知识群体、非公有制经济组织”并列为重要的党建力量。
1 研究区概况及研究资料
1.1 研究区概况
皂市水库位于湖南省常德市石门县,为大(Ⅰ)型年调节水库[10],以防洪、发电、供水等功能为主。坝址以上控制面积3 000 km2,多年平均流量99.3 m3/s。水库正常蓄水位140 m,总库容14.39 亿m3,兴利库容9.66 亿m3,防洪库容7.8 亿m3,死库容2.71 亿m3,有效库容11.68 亿m3,库容系数为0.3[11,12]。
百香果汁、胡萝卜汁、白砂糖、接种菌种、稳定剂黄原胶∶CMC(1∶1) 的添加量分别控制在4.0%,25.0%,10.0%,1.0%,0.1%;然后将发酵温度分别控制在41,43,45℃,研究产品的最佳发酵温度。
2021年皂市水库水质全年均为Ⅱ类水及以上,而澧水下游及环洞庭湖区的区县在枯水年份供水缺口较大,且供水水源为Ⅲ类水,用水矛盾突出,水资源配置能力不足。为满足优水优用、空间均衡的供水需求,常德市“十四五”水安全保障规划拟建设皂市引调水工程,以保障石门县、澧县、临澧县、津市市、安乡县的用水安全。因此,研究皂市水库的兼顾供水、发电、生态多目标的调度,有利于充分发挥水库功能,提高用水效率。皂市水库及其对各区县的供水路线概况如图1所示。
竹节蓼药材的HPLC指纹图谱建立及聚类分析…………………………………………………… 黎 理等(12):1640

图1 研究区概况Fig.1 Summary of study area
1.2 研究资料
水库基本数据资料包括:皂市水库的正常蓄水位、防洪限制水位、死水位、库容-水位关系曲线、下游水位-下泄流量关系曲线、水库发电机组出力约束值;水文资料为皂市站1953年-2021年的逐月流量数据。研究数据来自湖南省江垭和皂市水库管理处。对69年的径流系列进行频率计算,选择平水年、枯水年、特枯水年3种典型年进行分析,其中平水年选取1988年(P=50%),枯水年选取2013年(P=75%),特枯年选取2019年(P=95%)。
CEA正常范围:0~10×103 ng·L-1;CA19-9正常范围:0~37×103 ng·L-1;CA15-3正常范围:0~35×103 ng·L-1;NES正常范围:0~16×103 ng·L-1。
社会经济资料包括石门县、澧县、临澧县、津市市和安乡县的人口、工业增加值、灌溉面积、用水定额等数据,来自《常德市水资源公报(2017-2020年)》、《中国县域统计年鉴(2017-2020年)》、《湖南省水资源公报(2017-2020年)》及相关规划报告。采用定额法结合趋势法预测2030 规划水平年条件下的逐月需水总量,经计算,2030年总需水量为17.025亿m³,其年内分配过程如图2所示。

图2 2030年研究区需水量年内分配预测Fig.2 Forecast of annual water demand allocation in the study area in 2030
2 研究方法
首先建立面向发电、供水和生态的皂市水库多目标优化调度模型,而后采用多目标混合蛙跳差分进化算法(MSFL-DEA)与多属性决策的方法相结合的求解方法,该方法的总体思路是:利用MSFL-DEA 求解多目标优化问题,得到Pareto 最优解集;再采用AHP-TOPSIS组合赋权,在备选方案集中寻找符合决策者偏好的最优决策方案。
2.1 皂市水库多目标优化调度模型
2.1.1 目标函数
(1)社会效益:调度期内供水满足度最大。
式中:Qs,t为t时段皂市水库向澧水尾闾及洞庭湖腹地各县的供水流量,m3/s;T为总调度期时长,取值为12;Δt为计算时段长度,s;Wt为t时段的需水总量,m3。
(2)发电效益:调度期内总发电量最大。
Web页面除了提供对集成数据仓库系统的数据检索服务外,还包括添加新序列,序列同源搜索分析,序列的比对分析和分析结果的图像显示等服务。
式中:E为整个调度期内的总发电量,亿kWh;k为皂市电站发电综合系数,取k=8.75;Qt为t时段皂市电站发电引用流量,m3/s;Ht为t时段皂市电站发电净水头,m;Δt为计算时间长度,h。
(3)生态效益:生态流量满足度最高。
式中:cd(t)表示t时段河道生态流量满足度,无量纲;若河道内生态流量低于最小值,cd(t)取0;若介于最小值和适宜生态流量下限之间,取值范围为0~0.5;若介于适宜生态流量区之间,取值范围为0.5~1;若大于适宜生态流量区间上限,则记为1[13];Qdk(t)表示t时段皂市水库向河道下游的下泄流量,Qdk,min(t)表示生态流量约束下限,Qdk,max(t)表示生态流量约束上限;单位均为m3/s。考虑到研究区缺乏生态资料,参考张寒等[10]基于逐月频率法结合Tennant法预测的渫水生态流量结果,取逐月频率P=75%~25%为推荐适宜生态流量区间。
2.1.2 约束条件
(1)水量平衡约束。
水库的多目标优化调度需要考虑复杂的水力联系,同时还需要处理众多的约束条件,包括水量平衡约束、水库库容约束等:
式中:Qin(t)、Qout(t)分别表示为t时段的水库入库及出库流量,m3/s;V(t+1)、V(t)分别表示为t+1和t时段的水库库容,m3;Δt为计算时段长,s。
经过多次试算,MSFL-DEA算法参数设置为Np=200,N=10,M=20,G=1 000,K=12,F0=0.5、CR=0.3,NEA=90,进而求解得到皂市水库平(50%)、枯(75%)、特枯(95%)3 种频率来水输入条件下皂市水库供水、发电和生态多目标的非劣调度方案集,Pareto前沿在两两目标上的投影分别如图3~5所示。
式中:Vmin(t)、V(t)、Vmax(t)分别表示为t时段水库的最小库容、实际库容以及最大库容,m3。其中汛期(4-7月)允许最高水位为防洪限制水位,对应库容6.049 亿m3,非汛期(8月至翌年3月)允许最高水位为正常蓄水位,对应库容11.998 亿m3,最小库容为死库容2.691 亿m3。
(3)出库流量约束。
式中:Qmin(t)、Qmax(t)分别表示为t时段水库的最小及最大下泄流量,m3/s;最大下泄流量依据皂市水库工程特性,取设计洪水位最大下泄流量12 526 m3/s。最小下泄流量依据《水利部关于印发澧水流域水量分配方案的通知》,在现状通航条件下,取近期水平年的最小下泄流量为22.0 m3/s。
新中国成立后,爷爷奶奶成为地道的贫苦农民,每天早出晚归,参与人民公社集体耕作挣工分,晚上熬夜纺棉花,养活儿女。后来赶上物质极度匮乏的三年自然灾害,家里常常无米下锅,爷爷奶奶想着法子续上一家子的性命,吃野菜、啃树皮,穿衣更是“新老大,旧老二,缝缝补补给老三”,最终挺过粮食关。这段时期,这对银镯子成了家里最值钱的东西。
(4)皂市电站出力约束。
式中:Nt表示t时段皂市电站的发电出力,MW;Nmin、Nmax分别为t时段皂市电站的最小发电出力、最大发电出力,分别取18.3、120 MW。
2.2 基于MSFL-DEA的优化调度模型求解
2.2.1 模型编码
皂市多目标优化调度模型是以月为单位的中长期优化调度模型,调度周期为年,则模型的时段长度T=12。模型选择皂市水库在各时段初(末)水库库容V(t)为状态变量,对应决策变量维度DV=13。由于皂市水库还需要向澧水下游及洞庭湖区供水,模型将供水流量Qs,t也作优化,对应供水流量的决策变量维度DQ=T=12。因此,模型决策变量维度D=DV+DQ=25,如下所示:
2.2.2 计算步骤
确定模型编码后,分别选取50%、75%、95%三种频率来水作为模型输入,调度起止时段设置为4月至次年3月,设置各水库初水位为汛限水位,末水位为相应典型年来水输入条件下的常规调度结果末水位。采用多目标混合蛙跳差分进化算法[8]对模型进行求解,计算步骤如下:
限于篇幅限制,选用标准函数DTLZ2和DTLZ7[14]对MSFLDEA 算法进行测试,采用反向世代距离(IDG)[15]和超体积指标(HV)[16]综合表现算法的收敛性和多样性,并与常用的算法结果进行对比,包括多目标粒子群优化算法(MOPSO)[17]、快速非支配排序进化算法(NSGA-III)[18]、基于分解的多目标进化算法(MOEAD)[19]。对比结果如表1所示,IDG 值越小,HV 值越大,代表算法的性能越优良。
微生物制剂在我国水产养殖事业发展中发挥着巨大的推动作用,有着非常广阔的发展空间。微生物制剂不但能够促进养殖产品的快速生长、繁衍,还可以减小水产养殖成本、降低对环境的污染。微生物制剂作为一种绿色无污染的添加剂,在未来必然会获得人们的认同与大量应用。
(2)约束处理:某决策变量不满足约束条件时,将其适应度函数值取为接近于零的一个较小数值,确定输出的决策变量符合约束条件。
(3)初始化:基于混沌理论生成初始种群,随机选取D个[0,1]区间的内不同的初始值,构成初始序列,通过Logistic映射得到Np个轨迹不同的混沌序列;将混沌序列放大到各时段水库库容及供水流量的取值范围,得到Np个初始种群。
在应用过程中,水库运行往往只需要一组水库优化调度方案,基于2.2 求解得到的Pareto 调度方案集,采用AHP[20,21]与TOPSIS[22,23]的主客观组合赋权法,先通过AHP 计算发电量、供水满足度和生态满足度3 个指标的主观权重,通过一致性检验后,根据TOPSIS 计算每个非劣解到理想解的相对接近度S,优选得到组合赋权后各频率来水下的供水优先、发电优先、生态优先以及均衡方案。方法原理详见文献[23]。
2.炒锅置火上,放菜油烧至四成热,下干辣椒节炒几下,再下牛油炒热放豆瓣酱炒香,下姜片、蒜片,炸出香味,倒入鲜汤,用大火烧沸,下醪糟汁、精盐、冰糖,熬 10 min,下花椒熬出香味,舀入火锅中,打去浮沫,加入味精,即为汤汁。火锅点火,放入红枣、猪蹄块、蹄筋煮沸,便可随意烫食。
(5)随机排序:按照非劣等级对种群个体在各等级内随机排序,所有个体混合后划分N个子种群,每个子种群个体数为M,选择子种群中第M个个体为子种群最差解。
(6)局部搜索更新:基于自适应策略差分算法更新各子种群中的最差解,主要包括变异、交叉、选择3种操作。
(7)子种群混合:各子种群局部搜索完成后,将所有个体混合,重新组合成Np个个体的种群,转入步骤(4)。
(5)对照1组与对照2组采用新鲜土豆片外敷,马铃薯系薯类食物,属茄科植物,含有大量淀粉、各种盐类及龙葵素等。龙葵素有缓解痉挛、减少渗出的作用,局部外敷有消肿止痛作用。中医认为马铃薯具有清热解毒、消肿散瘀的作用,现代医学证明:马铃薯中的茄碱能够降低组织渗透性,抑制透明质酸酶活性和抗组胺作用而具有消炎及抗过敏作用。但临床效果观察及对比研究显示,采用中西药交替外敷对防治化疗性静脉炎效果更显著。
(8)判断是否达到预定的全局迭代次数G,若没有达到,转入步骤(4);否则,算法结束,输出EA中的Pareto最优解集。
2.2.3 数值计算分析
(1)参数设定:设置初始种群规模Np、子种群数N,每个子种群个体数量M,全局迭代次数G,子种群迭代次数K,变异率F0、交叉率CR,外部档案集NEA。
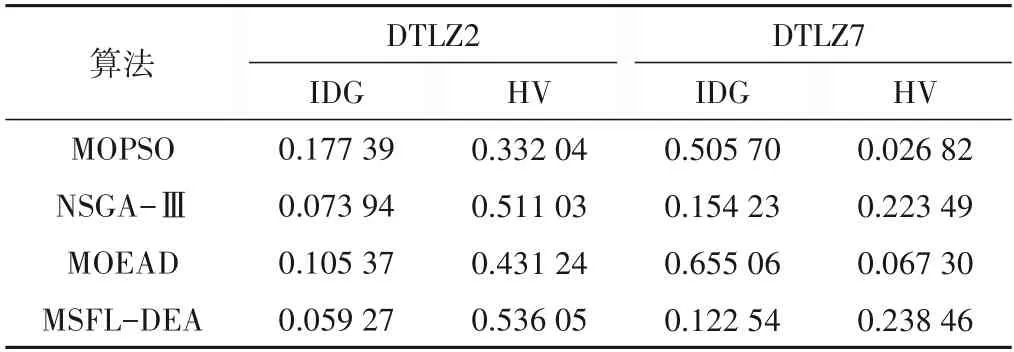
表1 各算法测试结果对比Tab.1 The test results comparison of each algorithm
由表1可见,MSFL-DEA 算法的IDG指标均小于其余算法,HV 指标均大于其他算法,表明MSFL-DEA 算法的种群多样性强,可以更好地避免陷入局部最优,算法的寻优性能也更高,具有较好的收敛性。
春天的田野是美丽的:蔚蓝的天空中,慢悠悠地飘过一朵朵洁白无瑕的云,它们没有线条,就像只用白色颜料泼出来一般,随意而自由。山路两旁有成片的野酸枣树、桃树、山楂、野荆,这个时节有些果木正好开花,成群的蜜蜂嗡嗡地在花丛间飞来飞去,一刻不闲地忙碌着。纵横交错的河支细干在小山村中纵情蜿蜒,河水清澈甘冽,调皮的鱼儿在纤柔的水草间来回穿行,时不时吐出一串串晶莹的水泡。这真是一幅美丽的春景图。
2.3 基于AHP与TOPSIS组合赋权的方案优选
(4)目标函数计算:计算每个个体的各个目标函数值,进行非支配排序,依据动态更新机制更新外部归档集(EA),随机选择全局最优解Gbest。
3 结果分析
3.1 多目标关系分析
(2)水库库容约束。

图3 不同来水频率下发电、供水目标二维投影Fig.3 Two-dimensional projection of power generation and water supply targets under different inflow frequencies
图3 反映随着生态满足度的变化,不同频率来水条件下供水目标和发电目标之间的关系。当生态满足度较低时,发电量随供水满足度的增加呈现明显的减小趋势,生态满足度较高时,发电量和供水满足度关系变化不明显;当生态满足度增大时,供水目标和发电目标之间的点据呈现下移趋势,表现为供水效益随着生态效益的增大而减小。
图4 反映随着供水满足度的变化,不同频率来水条件下生态目标和发电目标之间的关系。当供水满足度为定值时,发电量会随生态满足度的增加而减小,即供水效益会随发电效益的提高而减小;当供水满足度增大时,生态目标和发电目标之间的点据呈现下移趋势,表现为生态效益随着供水效益的增大而减小。

图4 不同来水频率下发电、生态目标二维投影Fig.4 Two-dimensional projection of power generation and ecological targets under different influent frequencies
图5 反映随着发电量的变化,不同频率来水条件下生态目标和供水目标之间的关系。当发电量为定值时,供水满足度会随生态满足度的增加而减小,即供水效益会随生态效益的提高而减小;当发电量增大时,生态目标和发电目标之间的点据呈现下移趋势,表现为生态效益随着发电量的增大而减小。

图5 不同来水频率下供水、生态目标二维投影Fig.5 Two-dimensional projections of water supply and ecological objectives under different inflow frequencies
根据图3~5,随着水库上游来水的减少,流域供水满足度从0.75~0.92(P=50%)减小至0.55~0.75(P=95%),下降程度约为22.6%;水库水电站发电量从3.62~4.07 亿kWh(P=50%)减少至2.03~2.30 亿kWh(P=95%),下降程度约为43.7%;而皂市水库下游河道的生态满足度从 0.54~0.90(P=50%)减少至0.39~0.68(P=95%),下降程度约为26.1%。水库的供水、发电和生态目标满足度均随着来水量的减少而得到不同程度的降低,发电效益降低程度最为显著。总体而言,皂市水库生态、发电和供水目标之间呈现竞争关系,其中,生态目标与发电目标、供水目标与生态目标的竞争关系相对更为明显,而发电目标和供水目标间的竞争关系相对较弱。考虑水库发电用水下泄后还可以被用水区域利用,因此发电和供水两个目标之间的竞争性相对较弱。
3.2 优选方案分析
根据2.3 计算得到各来水频率下的供水优先、发电优先、生态优先以及均衡方案,不同方案在非劣解集中的位置如图6所示。
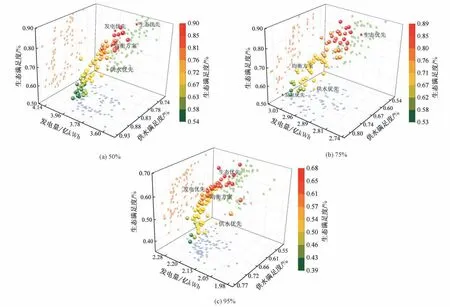
图6 不同频率来水非劣解集分布结果Fig.6 Distribution results of non-inferior solutions under different inflow frequencies
统计各方案目标值,如表2所示。不同来水下,均衡方案到理想解的相对接近度S均最高。供水优先方案除供水目标最优,发电量和生态满足度都较低;发电优先方案的发电目标最优,在P=50%和P=95%频率来水情况下,生态满足度略高于均衡方案,但供水满足度较低,P=75%时情况相反;生态优先方案的生态满足度最高,但供水满足度明显较小,P=75%和P=95%时发电量也较低,P=50%时则略高于均衡方案;在P=50%、75%、95%三种频率来水情况下,均衡方案比单一优先方案的最高指标值降低约4.29%、12.08 和5.15%,但比指标最低值增加8.56%、18.14%和9.73%,对发电、供水和生态3个目标的改善程度更高。随着来水量的减少,三种目标值均有所降低,在各频率来水情况下,单一目标优先的方案均以牺牲其他目标为代价,而均衡方案偏向折中,更为协调。
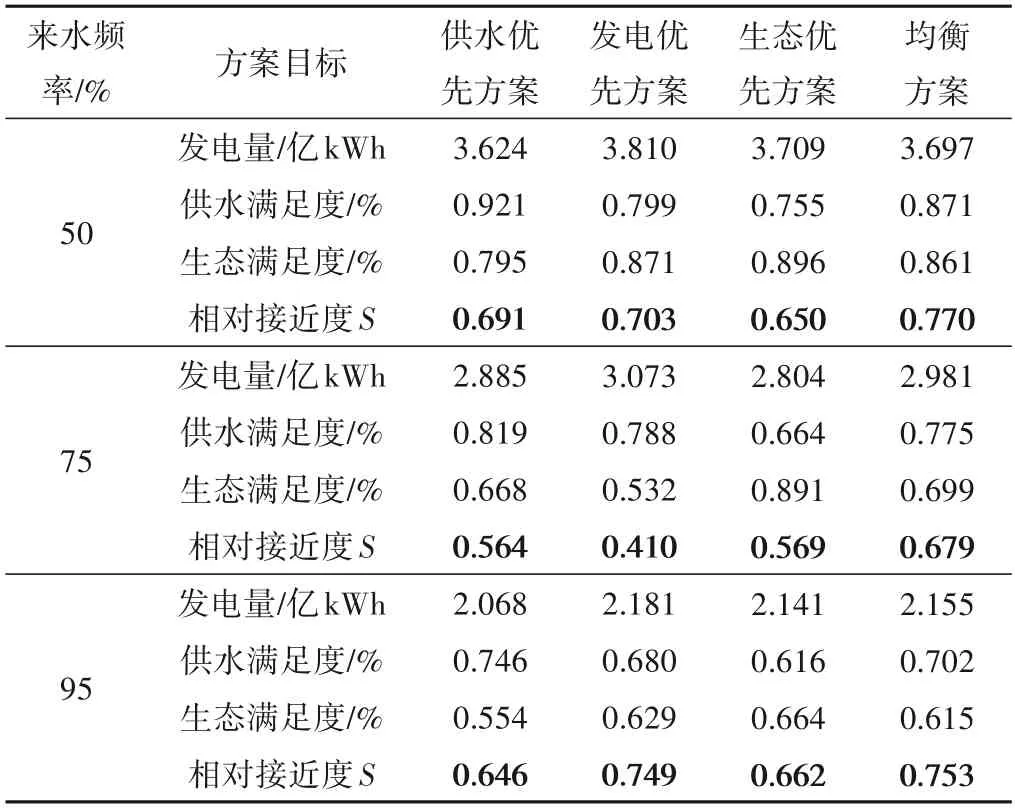
表2 各频率来水下不同调度方案目标值Tab.2 The target value of different underwater scheduling schemes under different frequencies
3.3 典型方案调度过程分析
选取供水优先、发电优先、生态优先和均衡方案这4个典型方案,以75%频率来水条件为例,分别绘制各方案的皂市水库水位过程、下泄流量、水库发电量及供水满足度图,如图7所示。

图7 75%频率来水各方案调度过程Fig.7 Different scheduling processes under 75% frequency influent condition
根据图7(a),汛期4-7月份供水优先方案水位较低,非汛期8月-次年3月生态优先方案水位较低,6月起发电优先方案的水位逐渐高于其他方案。整体而言,水库水位过程增长和消落趋势基本同步,但是水位差异明显。供水优先方案的水位过程相对较低;发电优先方案的水库消落度相对较大,更有利于发电;生态优先方案的水库水位过程相对平缓,消落度小;均衡方案的水位过程介于其他方案之间。
根据图7(b),各方案4-10月份用水区域的缺水程度较大,11月-次年3月的供水量都能满足研究区的需水要求,主要原因在于4-10月的农业需水占比高。供水优先和均衡方案各月的供水满足度整体较高,但是9月份供水优先方案的下泄流量极低,生态破坏程度严重;生态优先和发电优先方案的供水满足度起伏较大,其中4月份生态优先方案的供水满足度最低,仅为8.36%,远低于其他方案,但下泄流量处于适宜生态流量区间范围内;7月份各方案的供水满足度处在13%~20%之间,这是因为7月份为下游区县需水最大的月份,农业需水占全年的28.5%,同时该月生态下流流量也相对较低。
根据图7(c),生态优先方案各月的下泄流量均高于最小生态流量,且大多处于适宜生态流量区间范围内;供水优先方案的下泄流量大多月份低于均衡方案,但除9月份外,都高于最小生态流量;发电优先方案和均衡方案的下泄流量起伏较大,5月、7月和8月均低于最小生态流量,但发电优先方案的下泄流量更低,生态破坏程度更大。
根据图7(d),发电优先方案6月和10月的发电量峰值高,年发电总量大,但下泄流量较大,超出适宜生态流量上限,且5月、7月、8月、12月的发电量处于较低水平;均衡方案发电量在6月和9月较高,下泄流量处于适宜生态流量区间范围内,但1月、2月的发电量较低;年总发电量仅次于发电优先方案;供水优先方案和生态优先方案的发电量年内起伏较小,其中生态优先方案的发电量在9-11月处于较低水平,而供水优先方案的各月发电量介于其他方案之间,差异较小,年总发电量低于发电优先方案及均衡方案。
(4)将第4行对角元以右的1个元素赋值给对角元以下的1个元素;再对第4行的1个元素规格化;继而对第4列元素消元,仅计算虚线框中的1个元素,见图5下图。
4 结论
研究以水库发电量最大、下游生态流量满足度最大以及石门县等下游区县供水满足度最大为优化目标,在P=50%、75%和95%三种不同频率来水条件下,构建了面向供水、发电和生态的皂市水库多目标供水调度模型,采用多目标混合蛙跳差分进化算法进行求解,并基于AHP 和TOPSIS 组合赋权法进行方案优选,得到结论如下。
(1)依据多目标关系分析,在不同频率来水条件下,随着水库上游来水的减少,供水、发电和生态效益呈现不同程度的降低,其中发电效益下降最为显著,其次为生态效益和供水效益;在相同频率来水条件下,生态目标与发电目标、供水目标与生态目标的竞争关系相对更为明显,而发电目标和供水目标间的竞争关系相对较弱。
鞋子华丽、高贵,这在以前,李若定然是发狂地欢喜,这是她梦寐以求的事。可是当她真的站在琳琅满目的橱窗前,心却是灰的。
(2)依据组合赋权法得到各频率来水下的供水优先、发电优先、生态优先以及均衡方案,可根据决策者的偏好进行方案选择,其中均衡方案在满足年发电量、年供水满足度和年生态满足度均相对较高的同时,对其他方案最低值的改善程度高于对最高值的削减程度,且年内各月的供水、生态及发电过程也相对协调(以P=75%为例)。均衡方案的优化调度结果为:P=50%时,年发电量为3.697 亿kWh,供水满足度为0.871,生态满足度为0.861;P=75%时,年发电量为2.981 亿kWh,供水满足度为0.775,生态满足度为0.699;P=95%时,年发电量为2.155 亿kWh,供水满足度为0.702,生态满足度为0.615。

