兼顾满意与稳定的应急救援服务供需匹配决策

张 笛，张 娜，闫书丽

1.南京信息工程大学 商学院，南京210044

2.南京信息工程大学 江北新区发展研究院，南京210044

3.南京信息工程大学 管理工程学院，南京210044

突发事件是指突然发生，造成或者可能造成严重社会危害，需要采取应急处置措施予以应对的自然灾害、事故灾难、公共卫生事件和社会安全事件等[1]。21世纪以来，突发事件在全球各国时有发生，如2003 年的“非典型肺炎”疫情、2004 年的印尼海啸灾害、2005 年的飓风“卡特里娜”灾害、2008年的汶川“5·12”地震和南方特大雪灾害、2011年的日本福岛核电站泄漏事件、2012年的“7·21”北京特大暴雨灾害、2013年的超强台风“海燕”灾害、2019 年因高温干旱引发的澳大利亚丛林大火事件、2020 年的“新型冠状病毒感染”疫情以及2021 年的河南特大暴雨灾害。突发事件不仅严重威胁着人民群众的生命与财产安全，且对社会运行体系产生严重冲击，其所特有的紧迫性与不确定性给社会发展带来了极大的挑战。开展突发事件应急救援，提高应急处置能力，对降低突发事件造成的人员伤亡和财产损失具有重要的现实意义和实践价值。

民间救援组织已成为中国特色应急救援力量的重要组成部分之一，并逐渐成为突发事件应急救援的一支重要力量。近年来，学者们从不同的视角出发，采用不同的理论与方法研究突发事件应急救援人员分配问题[2-15]，概括起来现有研究文献大体可以分为三类：一是基于多准则决策理论，着重从群决策的视角优化应急救援方案的决策过程[2-4]。马齐飞扬等[2]针对列车突发事件的应急救援问题，构建了多Agent 的应急救援组织结构，建立基于改进TOPSIS 的应急救援决策方法。李海涛等[3]考虑突发事件应急救援决策中专家面临多元不确定信息问题，提出一种基于多元不确定信息的灰色局势群体应急决策模型。宋英华等[4]研究了地震灾害应急救援决策中专家偏好的冲突问题，建立基于D-S证据理论的应急救援群决策方法。基于群决策视角的应急救援决策方法的本质是救援方案的排序问题，难以优化有限应急资源的利用效率，在实际应用中具有一定的局限性。二是基于“效率”优化的视角，建立应急救援人员指派模型[5-12]。张雷等[5-6]考虑突发事件应急救援的效率、时间以及救援物资约束等因素，建立突发事件应急救援人员的多目标指派模型。袁媛等[7]、李铭洋等[8]以及Li等[9]针对多救援点的突发事件应急救援派遣问题，通过集结救援人员关于救援点的胜任度和救援时间的满意度，建立基于综合匹配度的应急救援人员指派模型。Wex等[10]、Zhang等[11]以及Rauchecker等[12]从调度的视角，研究突发事件应急救援的响应问题，根据突发事件的严重程度，以完成应急救援时间最小为目标，建立应急救援决策支持模型。应急救援人员指派方法是通过建立数学优化模型来提高有限应急资源的利用效率，其本质是传统的单向指派模型，忽视了应急救援服务供需双方的偏好表达[13-15]。三是双向考虑应急救援服务供需双方的偏好信息，基于双边匹配的视角，构建应急救援服务供需双边匹配模型[13-15]。陈圣群等[13]针对经典突发事件应急救援人员单向指派模型的不足，建立考虑同群效应的突发事件应急救援双边匹配模型。杨琴等[14]考虑应急救援人员的心理行为因素，提出一种基于前景理论的突发事件应急救援人员双边匹配方法。Chen 等[15]研究了突发事件应急救援中的信息不确定问题，建立基于证据推理和前景理论的应急救援人员双边匹配模型。

上述研究文献丰富、发展和完善了突发事件应急救援人员分配理论与方法，需要指出的是现有突发事件应急救援人员分配问题是一个典型的双边匹配问题[13-15]。目前，从双边匹配的视角，研究应急救援人员分配问题的文献极少，虽可以看到相关研究成果[13-15]，但现有研究大多是基于匹配的满意性视角，构建的应急救援服务供需双边匹配模型，极少关注应急救援服务供需双边匹配的稳定性。在双边匹配中，匹配的稳定性是不可忽视的重要因素，匹配的稳定性不仅是衡量双边方案优劣的重要依据，且与双边匹配结果的满意程度密切相关[16-19]。稳定匹配起源于Gale和Shapley[16]关于学生入学和婚姻匹配问题的研究，Gale 和Shapley 提出了稳定匹配的定义，证明了稳定匹配的存在性，提出了稳定匹配的延迟接受“G-S”算法，开启了双边匹配理论研究的先河。Roth等[17]通过引入线性规划理论，构建了基于优化模型的一对一稳定双边匹配模型。袁铎宁等[18]考虑了存在岗位占有情形下的人岗双边匹配问题，建立一种岗位存在占有申请者条件下的双边匹配模型。张笛等[19]考虑了具有模糊语言偏好信息的双边匹配问题，提出一种满意公平稳定双边匹配方法。突发事件应急救援服务供需匹配的稳定性具有重要的意义和作用，若单纯考虑匹配的满意性，而忽视双边匹配的稳定性，则可能导致双边匹配方案失效，进而降低突发事件应急救援的效率。鉴于此，本文综合考虑突发事件应急救援服务供需匹配的满意性和稳定性，提出一种兼顾满意与稳定的突发事件应急救援服务供需双边匹配方法。

1 应急救援服务供需匹配问题描述

为了便于描述与分析，下面给出突发事件应急救援服务供需双边匹配问题的基本设置。

X={X1,X2,…,Xm} ：是突发事件紧急救援任务构成的集合，其中Xi表示X中的第i个紧急救援任务，i∈M={1,2,…,m},m≥2 且为正整数。紧急救援任务是突发事件应急救援服务的需求方，紧急救援任务的数量一般由突发事件应急救援协调中心确定。

Y={Y1,Y2,…,Yn} ：是中国民间公益性专业救援组织中救援服务队构成的集合，其中Yj表示Y中的第j个救援服务队，j∈N={1,2,…,n},n≥2 且为正整数。救援服务队是突发事件应急救援服务的提供方，是中国民间专业的纯公益紧急救援机构。救援服务队员以志愿服务为原则，以提供免费紧急救援服务为宗旨。

Pi=(pi1,pi2,…,pin)(i∈M)：是应急救援服务需求主体Xi给出的关于应急救援服务提供方Y的完全严格偏好向量，其中pij(pij∈N,i∈M,j∈N)表示紧急救援任务（紧急救援任务负责人）Xi对救援服务队Yj的偏好序信息，满足对∀j,j′∈N,当j≠j′时，有pij≠pij′，且pij越小，表明Xi越偏好Yj。

Qj=(q1j,q2j,…,qmj)(j∈N)：是应急救援服务提供主体Yj给出的关于应急救援服务需求方X的完全严格偏好向量，其中qij(qij∈M,i∈M,j∈N)表示救援服务队Yj对紧急救援任务Xi的偏好序信息，满足对∀i,i′∈M,当i≠i′时，有qij≠qi′j,且qij越小，表明Yj越偏好Xi。

突发事件应急救援服务供需双边匹配问题如图1所示。突发事件应急救援协调中心（简称救援协调中心）是以现代信息技术为基础，集通信、调度和指挥于一体的突发事件应急系统，其根据突发事件的实际情况，启动不同级别的应急救援响应[20]。

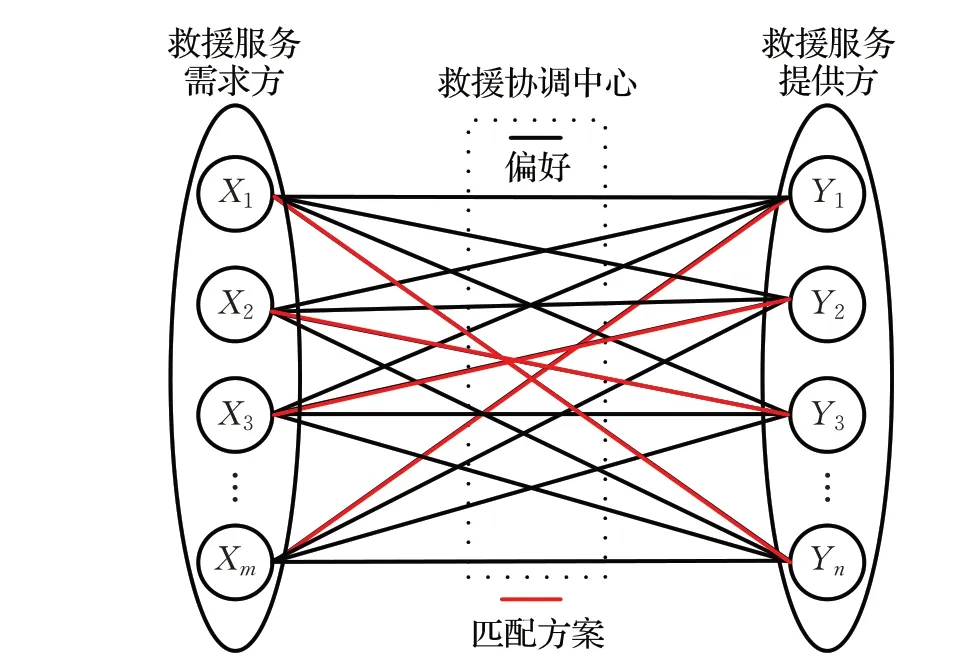
图1 救援服务供需匹配Fig.1 Matching of rescue service supply and demand

本文需要解决的问题是：在应急救援服务需求方的偏好向量Pi=(pi1,pi2,…,pin)(i∈M)以及应急救援服务提供方的偏好向量Qj=(q1j,q2j,…,qmj)(j∈N)的基础上，如何获得一种兼顾满意与稳定的突发事件应急救援服务供需双边匹配方案。

2 救援服务供需匹配模型

PROMETHEE Ⅱ[21]是一种基于方案两两优势比较的决策分析方法，具有操作简单、经典有效以及稳定性强的特点。为了解决突发事件应急救援服务供需双边匹配问题，本文借鉴PROMETHEE Ⅱ两两比较的思想，突发事件应急救援服务供需双方中的一方主体通过将另一方主体进行两两优势比较，获得每个匹配主体的总优先指数，构建基于总优先指数的匹配满意度，建立兼顾满意与稳定的突发事件应急救援服务供需双边匹配模型。

2.1 匹配满意度

突发事件应急救援服务供需双边主体通过将另一方主体进行两两优势比较，获得关于另一方主体的总优先指数，构建关于总优先指数的匹配满意度函数。

设x1和x2是两个任意的正整数，则x1和x2之间的差异测度为：

根据PROMETHEE Ⅱ，构建一般形式的偏好函数。突发事件应急救援服务需求方X中的主体Xi将应急救援服务提供方Y中的主体Yj与主体Yk(k≠j)进行两两优势比较，则主体Yj相对于主体Yk的优先指数为：

其中，d(pij,pik)是偏好序pij和pik之间的差异测度；fi(Yj,Yk)表示主体Yj优于主体Yk的程度，当fi(Yj,Yk)≤0时，表示主体Yj和主体Yk之间无差异，当fi(Yj,Yk)=1时，表示主体Yj严格优于主体Yk。

设应急救援服务提供主体Yj相对于Y方中所有主体的总优先指数为，则其计算公式如下：

设αij是应急救援服务需求主体Xi关于应急救援服务提供主体Yj的匹配满意度，则其计算公式为：

其中，αij(0 ≤αij≤1) 是关于的单调递增函数，即越大则主体Xi关于主体Yj的匹配满意度越大；αij越大表明主体Xi与主体Yj相匹配的可能性就越大。

同理，突发事件应急救援服务提供方Y中的主体Yj将应急救援服务需求方X中的主体Xi与主体Xl(l≠i)进行两两优势比较，则主体Xi相对于主体Xl的优先指数为：

其中，d(qij,qlj)是偏好序qij和qlj之间的差异测度；gj(Xi,Xl)表示主体Xi优于主体Xl的程度，当gj(Xi,Xl)≤0时，表示主体Xi和主体Xl之间无差异，当gj(Xi,Xl)=1时，表示主体Xi严格优于主体Xl。

设应急救援服务需求主体Xi相对于X方中所有主体的总优先指数为，则其计算公式如下：

设βij是应急救援服务提供主体Yj关于应急救援服务需求主体Xi的匹配满意度，则其计算公式为：

2.2 满意稳定匹配

设A={μ1,μ2,…,μt} (t≥2) 是由有限个突发事件应急救援服务供需双边匹配方案构成的方案集合。xij∈{0,1}，当xij=1 时，表示紧急救援任务Xi与应急救援队Yj匹配，当xij=0 时，表示紧急救援任务Xi与应急救援队Yj不匹配。下面分别介绍满意匹配[22-24]和稳定匹配的概念[16-19，25]。

若μk是方案集A的匹配方案，是μk对应的双边匹配满意度，若满足v(μk)=max{v(μi)|μi∈A},则称μk是一个满意匹配方案。

满意匹配的含义是在匹配方案集中，使得双边主体匹配满意度之和最大的方案。

设μ是一匹配方案，Xi∈X,Yj∈Y,pij,pik∈Pi,qij,qlj∈Qj，若μ满足下列条件之一，则称Xi和Yj是阻碍稳定对：

（1）∃Xl∈X,Yk∈Y,使 得μ(Xi)=Yk,μ(Yj)=Xl,且pij ＜pik,qij ＜qlj；

（2）∃Yk∈Y,使得μ(Xi)=Yk,μ(Yj)=Yj,且pij ＜pik；

（3）∃Xl∈X,使得μ(Xi)=Xi,μ(Yj)=Xl,且qij ＜qlj。

若μ中不存在阻碍稳定对，则称μ是稳定匹配方案。

若μ既是满意匹配又是稳定匹配，则称μ是满意稳定匹配方案。

2.3 满意稳定匹配模型

在突发事件应急救援服务供需双边匹配问题中，综合考虑双边匹配的满意性和稳定性，即以最大化应急救援服务供需双方的匹配满意度为目标函数，结合稳定匹配约束条件，建立突发事件应急救援服务供需双边匹配模型（8）～（13）。

式（8）的含义是最大化应急救援服务需求方X的匹配满意度；式（9）的含义是最大化应急救援服务提供方Y的匹配满意度；式（10）的含义是每个应急救援服务需求方至多与应急救援服务提供方中的一个主体相匹配；式（11）的含义是每个应急救援服务提供方至多与应急救援服务需求方中的一个主体相匹配；式（12）表示稳定匹配约束条件；式（13）的含义是应急救援服务供给与需求双边匹配的数量约束。式（10）和式（11）是为了提升突发事件应急响应能力以及最大化地提高有限救援服务资源的利用效率而设置的一对一双边匹配约束条件。

定理1若双边匹配μ满足约束条件式（12），则双边匹配μ是稳定匹配。

证明考虑定理1 的逆否命题与原命题的同真性，下面证明定理1 的逆否命题是真命题，即若双边匹配μ是不稳定的，则μ不满足约束条件式（12）。

在突发事件应急救援服务供需双边匹配模型（8）～（13）中，目标函数的量纲量级相同，因此可以使用线性加权和法将其转化为单目标线性规划模型（14）～（18）。

在模型（14）～（18）中，因xij∈{0,1},i∈M,j∈N，故单目标规划模型（14）～（18）是可行域有界的整数规划模型。又易知是模型（14）～（18）的一个可行解，故模型（14）～（18）的可行域非空。依据线性规划理论，模型（14）～（18）存在唯一的最优解，且模型（14）～（18）的最优解是多目标优化模型（8）～（13）的一个有效解。

3 算例分析

考虑突发暴雨灾害应急救援服务供需匹配问题。2021 年7 月DM 市某区因突发暴雨引发洪水和山体滑坡灾害，居民区受灾严重，道路严重损毁，数名群众滞留被困，情况十分危急，急需救援。灾害发生后，居民区的4 个受灾点{X1,X2,X3,X4} 需紧急救援（救援服务需求方，即紧急救援任务），当地及邻区的6支民间专业救援队{Y1,Y2,Y3,Y4,Y5,Y6} 申请参与一线救援服务（救援服务提供方）。应急救援协调中心依据救援队拟到达时间、一线搜救经验和所拥有的救援设备等信息对应急救援服务提供方进行偏好评价，给出6支救援队的偏好序信息如表1 所示。应急救援服务提供方根据受灾点位置、被困群众数量以及降雨地质等信息对应急救援需求方进行偏好评价，给出4个紧急救援任务的偏好序信息如表2 所示。应急救援协调中心依据双方的偏好进行匹配决策。

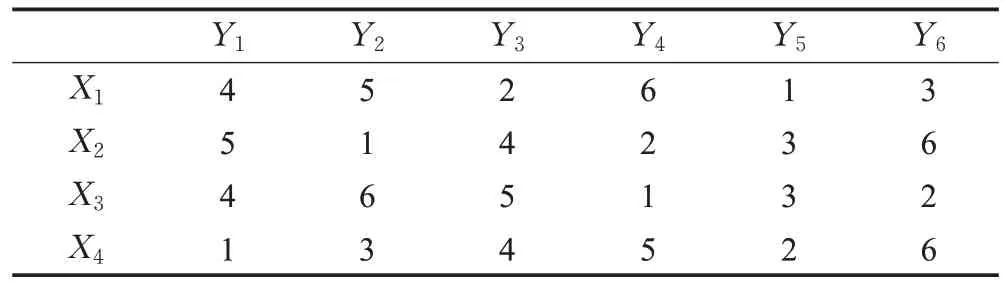
表1 救援协调中心给出的偏好信息Table 1 Preference informations given by rescue coordination center

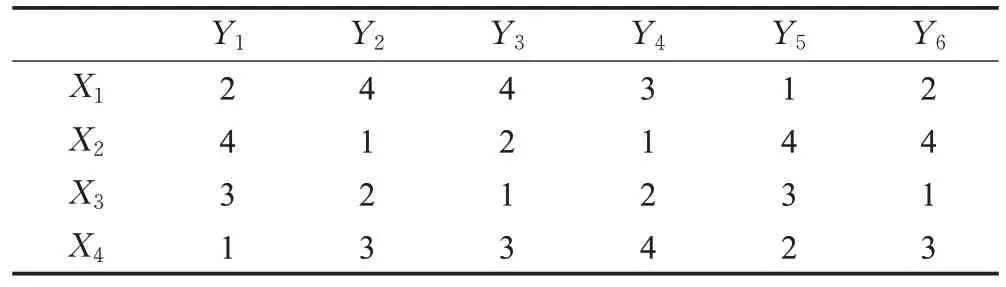
表2 救援服务提供方给出的偏好信息Table 2 Preference informations given by rescue service providers

3.1 计算过程

为了解决突发暴雨灾害应急救援服务供需匹配问题，采用前文提出的双边匹配方法，下面给出计算过程和结果。

然后，利用式（4）计算应急救援服务需求主体Xi关于应急救援服务提供主体Yj的匹配满意度αij，构建应急救援服务需求方X的匹配满意度矩阵。同理利用式（7）可得应急救援服务提供方Y的匹配满意度矩阵，具体如下所示：

最后，以最大化应急救援服务供需双方的匹配满意度为目标函数，结合稳定匹配约束，建立应急救援服务供需双边匹配模型（8）～（13）。根据权重系数ωX=0.60,ωY=0.40，采用线性加权和法将多目标优化模型（8）～（13）转化为单目标规划模型（14）～（17），具体如下所示：

使用Lingo11.0 软件求解上述模型，获得如下的计算结果：

3.2 结果分析

根据前文的计算结果，获得应急救援服务供需匹配方案：紧急救援任务X1与救援队Y5匹配（救援队Y5负责完成救援任务X1），紧急救援任务X2与救援队Y2匹配（救援队Y2负责完成救援任务X2），紧急救援任务X3与救援队Y4匹配（救援队Y4负责完成救援任务X3），紧急救援任务X4与救援队Y1匹配（救援队Y1负责完成救援任务X4），救援队Y3和Y6未匹配。应急救援服务需求方X的总体匹配满意度为2.40，应急救援服务提供方Y的总体匹配满意度为1.47，双边匹配满意度为3.87。

为了进一步说明本文方法的合理性和有效性，在突发事件应急救援服务供需双边匹配模型（8）～（13）中，不考虑匹配的稳定性，仅单纯考虑匹配的满意性，即在模型（8）～（13）中不考虑稳定匹配约束式（12），目标函数及其他约束条件保持不变（该模型是仅考虑匹配满意性的突发事件应急救援服务供需双边匹配模型）。为了增加可比性，仍采用线性加权和法求解模型，获得如下的计算结果：

即紧急救援任务X1与救援队Y5匹配，紧急救援任务X2与救援队Y2匹配，紧急救援任务X3与救援队Y6匹配，紧急救援任务X4与救援队Y1匹配，救援队Y3和Y4未匹配。应急救援服务需求方X的总体匹配满意度为2.28，应急救援服务提供方Y的总体匹配满意度为1.60，双边匹配满意度为3.88。表3 给出了两种不同应急救援服务供需匹配模型对应的匹配结果。

表3 不同匹配模型的匹配结果Table 3 Matching results of different matching models

从表3中可以看出，同时考虑满意与稳定的应急救援服务供需匹配模型的结果与仅考虑满意的应急救援服务供需匹配模型的结果不同，主要表现在以下几方面。

（1）应急救援服务供需匹配方案存在差异。在前者的匹配方案中X3与Y4匹配，Y3和Y6未匹配；在后者的匹配方案中X3与Y6匹配，Y3和Y4未匹配。

（2）应急救援服务供需匹配方案的稳定性不同。在前者的匹配方案中不存在阻碍稳定对，该方案是稳定双边匹配。在后者的匹配方案中，X3与Y6匹配，Y4未匹配，根据表1 可知p36＞p34，即相对于当前的匹配主体Y6,X3更偏好于Y4,且Y4未匹配，此时X3和Y4是阻碍稳定对，则该匹配方案是不稳定的，因阻碍稳定对各有更好的偏好选择，进而会放弃现有的匹配对象，导致现有的双边方案失效，因此极大地降低了突发事件应急救援供需匹配的效率（相对于稳定满意的匹配方案来说，不稳定的匹配方案是无效的匹配决策，不仅会增加匹配的成本，还会降低供需匹配的效率）。

（3）应急救援服务供需匹配方案的满意度存在微小差异。根据表3可以看出，两种模型对应的匹配满意度存在微小差异，前者的匹配满意度为3.87，略低于后者的3.88，在满意度方面二者的差异可以忽略不计。但相对于后者，前者是兼顾满意与稳定的匹配方案，不仅考虑了匹配的满意性，且保证了匹配的稳定性，因此能有效地提高突发事件应急救援的效率，减少无效的匹配决策以及降低匹配的成本。

4 结论

为了解决在突发事件应急救援服务供需匹配问题中，如何获得既“满意”又“稳定”匹配方案的难题，本文将PROMETHEE Ⅱ引入突发事件应急救援服务供需双边匹配，通过一方主体将另一方主体进行两两优势比较，获得每个匹配主体的总优先指数，构建基于总优先指数的匹配满意度函数。综合考虑突发事件应急救援服务供需匹配的满意性和稳定性，即以最大化应急救援服务供需双方的匹配满意度为目标，结合稳定匹配约束，建立兼顾满意与稳定的突发事件应急救援服务供需双边匹配模型，采用线性加权和法将多目标优化模型转化为单目标规划模型进行求解，获得一种兼顾满意与稳定的应急救援服务供需匹配方案。本文提出的突发事件应急救援服务供需匹配方法是从众多稳定的匹配方案中筛选出的使得双边主体匹配满意度最大的匹配方案，是一种兼顾满意与稳定的匹配方法，可避免因单纯考虑匹配的满意性，而忽视匹配的稳定性，导致匹配方案失效的现象。本文方法能有效提升突发事件应急救援服务的效率，减少无效的匹配决策，提高有限应急服务资源的利用效率，在实际应用中具有更强的适用性和可操作性。