面向二维近邻架构的启发式量子线路映射算法

徐怡然，仝梦楠，王菲，王海燕，沈洋，朱鹏程

（宿迁学院信息工程学院，江苏宿迁 223800)

0 引言

近年来，量子计算技术发展迅猛，IBM[1]、Google[2]以及中国科学技术大学[3-4]等多个科研机构相继发布了多种量子计算原型设备。这些设备由于量子比特资源有限以及量子操作易受噪声影响，通常也被称为中等规模带噪声量子设备[5]，简称为NISQ(Noisy Intermediate-Scale Quantum)设备。

在这些NISQ 设备上，每个物理量子比特仅允许和在设备拓扑结构中与其位置相邻的比特进行交互，这种约束被称为最近邻交互约束。最近邻交互约束要求量子线路中的双比特量子门仅允许作用在一对相邻的物理量子比特上，但是量子线路在设计时并未考虑物理设备上的最近邻约束，导致量子线路通常无法直接在NISQ设备上运行。

为了在NISQ 设备上运行量子线路，需要通过插入辅助量子门（如SWAP 门）的方式使得量子线路中双比特量子门均满足最近邻交互约束，将这种适配物理设备近邻交互约束所需的量子线路变换称为量子线路映射。量子线路映射对量子计算的实现代价和成功率有着重要影响，其是量子计算基础核心软件中必不可缺的组件。

1 相关工作

早期的量子线路映射研究主要面向此类一维的线性最近邻架构[6-11]，但随着量子计算技术的发展，目前基于超导电路以及离子阱等技术的量子计算设备通常采用二维最近邻架构，即量子比特分布在二维的平面架构图中。二维最近邻架构更复杂的连通性使得此前面向线性最近邻架构的量子线路映射方法通常不能直接适用于二维近邻架构。二维近邻架构上的量子线路映射已被证明是一种具有NP完全复杂性的计算难题[12]，目前关于面向二维架构的量子线路映射仍处于探索阶段，已有的研究存在较多有待完善之处。文献[12-13]将量子线路映射问题转换为PBO(pseudo Boolean optimization)问题，并通过SAT(Boolean satisfiability, SAT)/SMT(satisfiability modulo theories)求解器进行求解；文献[14-15]将映射问题形式化为CP(Constrained Planning)问题，并通过相应的TP/CP算法进行求解。以上方法由于指数级的时间复杂度，通常仅适用于求解规模极小的量子线路映射问题。IBM 的量子计算软件包Qiskit[16]提供了几种适用于大规模量子线路的启发式映射算法，其中性能最好的一种映射算法（简称SABRE)源于文献[17]，该方法基于对量子线路的正反向遍历技术对量子比特初始分配作全局优化，并构建了一种具有前瞻能力的加权代价函数和启发式映射规则。文献[12]的研究表明，现有的启发式方法由于其在搜索策略方面的局限性，仍存在很大的优化空间，特别是在较大型量子计算设备上，所得结果和最优结果之间的差距达5～45倍。

量子线路映射所需的辅助量子门数对量子线路的执行时间开销和成功率有着重要影响，为了在现有研究基础上进一步减少量子门数，本文对量子比特的初始分配策略和量子比特的动态路由策略进行了研究，并提出了基于量子比特权重优先级的初始映射算法和基于双重展望窗口的量子比特路由算法，实验结果表明，该方法可以有效降低映射插入的SWAP门数。

2 量子线路映射问题

量子线路映射通常包含两个关键工艺：量子比特初始映射和量子比特路由。其中初始映射用于将量子线路中的逻辑量子比特映射到设备上的物理量子比特上。在目前的NISQ 设备上，双比特量子门仅允许作用在位置相邻的一对物理比特上。初始映射对于最终量子线路的执行代价有着巨大影响，在不同初始映射下，执行线路中的双比特量子门所需的辅助量子门数存在巨大差异。由于量子线路中通常包含着多个双比特量子门，这些双比特量子门可能作用在不同的量子比特上，以及可能出现在线路中任意一个位置，所以多数情况下很难找到一个初始映射使得量子线路中所有双比特量子门均符合最近邻约束，在此情况下要通过插入SWAP门[16]在物理设备上移动逻辑量子比特，从而使得每个双比特量子门符合最近邻约束，将该过程称为量子比特路由。

将如图1 所示，量子线路映射到如图1(a)所示的二维网格型量子计算架构上，其中，图1(a)给出了量子比特初始映射，即{q0 →Q0, q1 →Q1, q2 →Q2,q3 →Q3, q4 →Q4, q5 →Q5, q6 →Q6, q7 →Q7,q8 →Q8}；图1(b)给出了量子比特路由过程，为执行该量子线路中的双比特量子门，共插入了4个SWAP门。

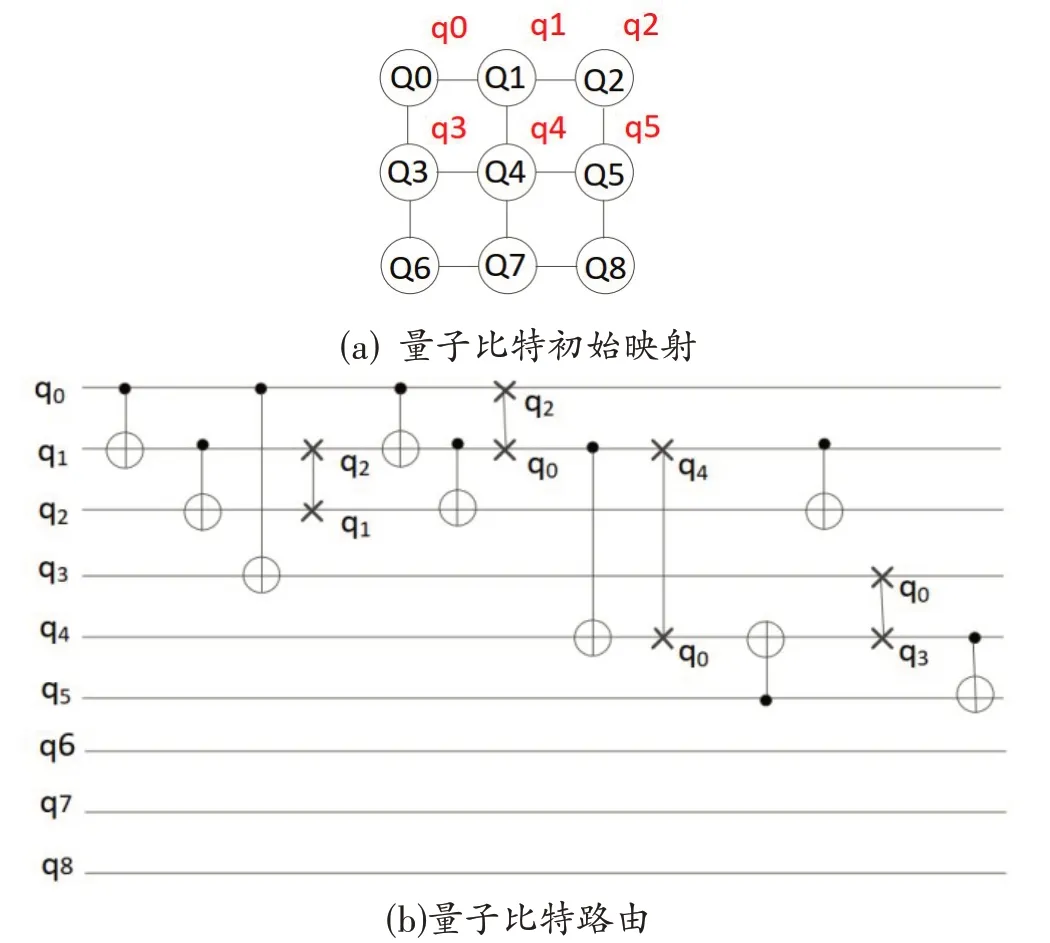
图1 量子线路映射过程

3 量子比特初始映射算法

量子比特初始映射用于为量子线路中的逻辑量子比特唯一且互斥的分配NISQ设备上的物理量子比特，本节将重点介绍用于生成量子比特初始映射的算法。

3.1 量子比特权重系数

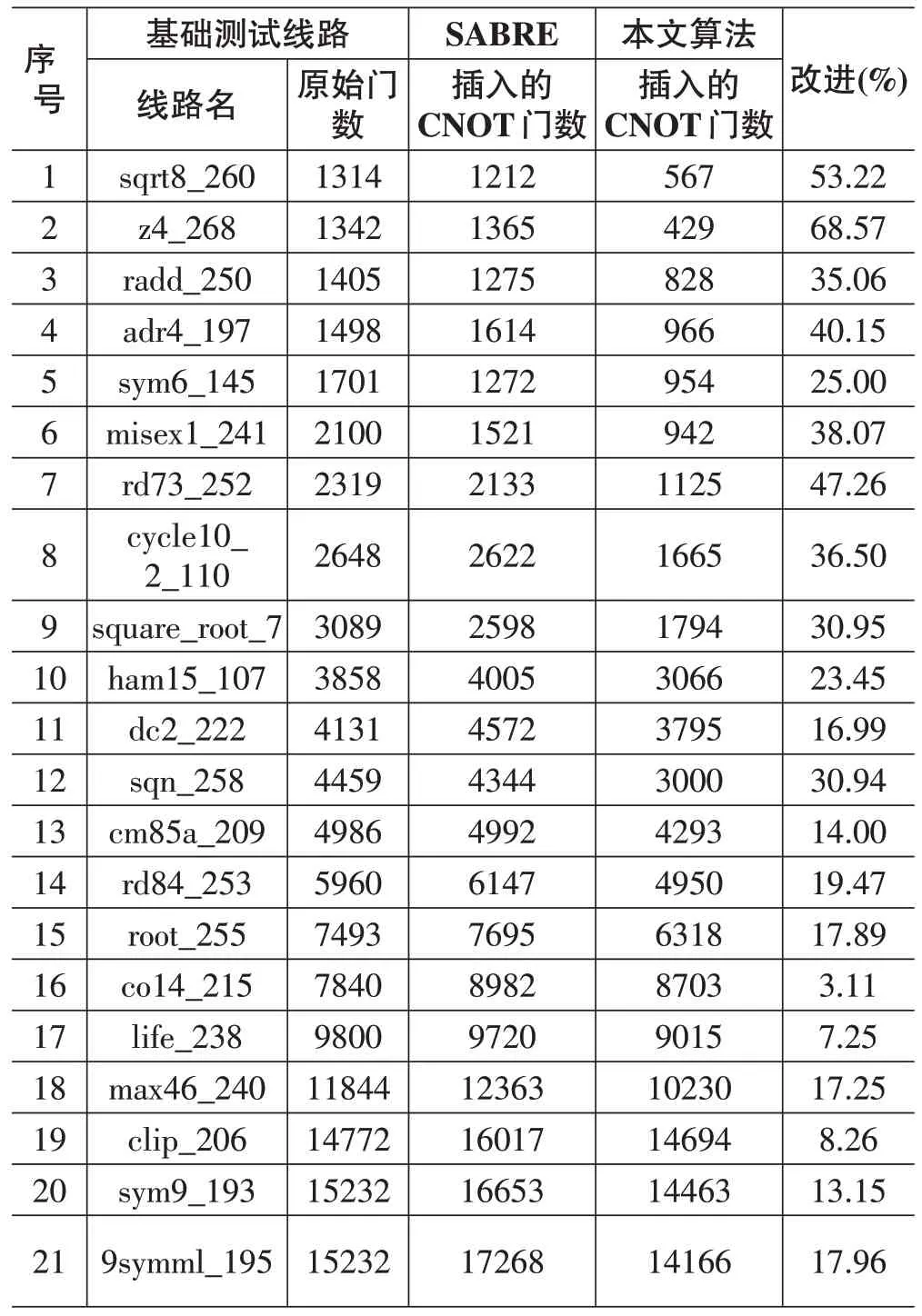
在量子线路中，每个量子比特可能和多个双比特量子门相关，在生成初始映射时，优先考虑关联量子门数较多的量子比特有助于降低映射代价，因此，可以使用所关联的双比特量子门数作为确定逻辑量子比特优先级权重的重要因素。另外，量子门的执行有严格的时序约束，量子比特权重系数同样也要考虑量子门的时序信息。基于以上因素，对于一个包含M个量子比特和N个量子门的量子线路，假设其第j个量子比特和第i个量子门相关联，其中，i(1<=i<=N)表示量子门的时序信息，j(0<=j

对于每个量子比特而言，与其关联的量子门赋予其的权重之和便是该量子比特的权重系数，如公式(2)所示。

量子比特权重系数决定了其在初始映射中的优先级，权重系数越大的量子比特对于降低量子线路映射代价具有更重要的作用，因此在初始映射时，将对线路中的逻辑量子比特按照其权重系数作降序排列，然后从前到后依次为序列中的各量子比特分配物理位置。

3.2 初始映射算法

在确定逻辑量子比特的权重优先顺序后，便可依次为每个逻辑量子比特分配设备上的物理量子比特。在分配逻辑量子比特qi时，在耦合上可能存在多个候选物理量子比特。为降低量子线路映射开销，应尽量将交互的逻辑比特分配至设备上的近邻位置。假定所有已分配的逻辑量子比特qx构成一个集合P，其中，逻辑量子比特qx对应的物理量子比特为Qloc(qx)，在将逻辑量子比特qi分配到物理量子比特Qj时所需的映射开销如公式(3)所示。

其中，d(Qi,Qj)表示物理量子比特Qi和Qj在设备架构图上的最短距离。x(i,j)表示量子比特qi和qj是否存在交互，即是否作为同一个双比特量子门的输入，若存在，则取值为1，否则取值为0。显然，公式(3)所示的代价函数越小，所需映射的映射开销也越少。

基于逻辑量子比特的权重序列以及公式(3)所示的映射代价函数，提出量子比特初始映射算法，如算法1所示。该算法的基本思想如下：为量子线路中的每个逻辑量子比特计算权重系数（公式(2))，并将逻辑量子比特按照权重系数降序排列；按照权重排序，每次选择一个逻辑量子比特，此时设备架构上所有空闲的物理量子比特均可作为该逻辑量子比特的目标位置，为选择最佳位置，为每个空闲物理量子比特计算映射代价函数（公式(3))，并将逻辑量子比特分配至映射代价最小的物理位置。

算法1 量子比特初始映射算法

输入：逻辑量子线路qc，量子设备架构图G

输出：量子比特的初始映射

1.根据公式(2)，为量子线路qc中的量子比特生成优先排序序列qu

2.FOR 序列qu中的每个逻辑量子qDO

3.FOR 架构图G中每个空闲物理量子比特QDO

4.根据公式(3)，计算将q分配Q的映射代价

5.记录映射代价最小的Qmin

6.END

7.将q分配至映射代价最小的Qmin

8.END

9.输出逻辑量子比特到物理量子比特的初始映射

4 量子比特路由算法

在给定的初始映射下，量子线路中可能仍然存在不满足近邻交互约束的双比特量子门，此时需要通过量子比特路由插入SWAP门，使得每个量子门均满足近邻约束。本节重点介绍量子比特路由相关的代价函数、规则以及算法。

4.1 启发式代价函数

给定量子比特初始映射π，一个量子门g 的映射代价如公式(4)所示。

其中，q1和q2表示量子门g 相关的两个逻辑量子比特；π(q)表示在初始映射π下逻辑比特q对应的物理比特；d()函数的含义和公式(3)相同，即表示两个物理量子比特在设备架构图上的最短距离。代价函数C(g)越小，则使该量子门满足近邻约束插入的SWAP门数越小。

在量子线路映射过程中，插入的SWAP门将交换所在物理量子比特上的逻辑量子比特，从而实现移动逻辑量子比特的效果。SWAP门对逻辑量子比特的移动将对后续量子门的映射代价产生连锁影响，因此为准确评价SWAP门的作用效果，需要考虑该门对其后所有量子门的影响，但对大规模量子线路而言这种做法的时间开销太高。因此，为在时间和代价之间取得平衡，通常仅考虑后续固定数目的量子门。为此引入展望窗口的概念，只有在展望窗口中包含的量子门才在计算映射代价时考虑。将应用SWAP门后，在展望窗口中所有量子门的映射代价（如公式(4))之和作为衡量一个SWAP门作用效果的代价函数。另外，量子线路中量子门的执行有着严格的时序关系，SWAP 门的作用代价函数应该更优先考虑执行时序靠前的量子门。基于该考虑，将展望窗口分为两级：第一级展望窗口F1包含量子线路中的前两层子线路；而第二级展望窗口F2包含量子线路中的第3～5 层子线路。从而得到如公式(5)所示的SWAP门代价函数。

其中，|F1|和|F2|分别是表示展望窗口F1和F2中包含的双比特量子门数；C(g)如公式(4)所示，表示双比特量子门的映射代价；ω 是一个权重因子，在实验时设置为0.8，表示代价函数优先考虑第一级展望窗口中的量子门。

4.2 启发式量子比特路由算法

量子比特路由算法按照量子门的依赖关系从左向右依次遍历量子线路中各量子门，若当前量子门满足近邻交互约束，则该量子门可立即执行，即将其从量子线路中删除；否则，需在多个可用SWAP 门中选择一个SWAP门用于移动逻辑量子比特，从而使得线路中某些待执行量子门逐步向着可执行状态转变。

算法2 启发式量子比特路由算法

输入：逻辑量子线路qc，量子设备架构图G，初始映射π

输出：满足近邻约束的物理量子线路

1.为量子线路qc生成量子门依赖关系图dag

2.WHILE 量子线路qc不为空DO

3.从依赖关系图dag中选择度为零的量子门，构成待执行量子门集合E

4.FOR 待执行量子门集合E中的每个量子门gDO

5.IF量子门g满足近邻约束THEN

6.从量子线路qc中删除量子门g，并跳转至第2行

7.END

8.根据待执行量子门集合E中的量子门生成可用SWAP门集合S

9.FOR 集合S中的每个SWAP门swDO

10.根据公式(5)，计算将SWAP门sw的代价函数

11.记录代价函数值最小的swmin

12.END

13.插入swmin，并更新初始映射π

14.END

本文提出的启发式量子比特路由算法如算法2所示，其中第3～7行用于执行在当前初始映射下满足近邻约束和量子门依赖关系的所有量子门；第8行中可选SWAP门集合S由设备所支持且至少和一个待执行量子门相关的SWAP 门组成；第9～13 行根据如公式(5)所示的代价函数在可用SWAP 门集合中选择一个代价函数值最小的SWAP门，将其插入量子线路并同时更新初始映射。当量子线路中的所有量子门均执行完成后，算法2终止运行。

5 实验与比较

本文所提全部算法均使用Python语言实现，运行环境为：Windows 10 操作系统、英特尔酷睿i5 处理器和8GB 内存。为检验本文映射算法的性能，将其和Qiskit 中集成的映射算法[16-17]作比较，即SABRE 算法。另外，所有实验中均采用了文献[16]相同的基准测试线路以及量子计算架构(IMB Q20)。由于在量子计算设备上SWAP 门需被分解成3 个CNOT 门，因此以CNOT门数实验评价标准。

SABRE 算法通过输入电路的迭代双向遍历对映射结果作优化，该方法具有很大的随机性，因此需要多次运行才能获得较好结果。为保证比较的公平性，实验中运行SABRE算法10次并取最优结果。具体实验结果如表1所示，本文所提方法和SABRE算法相比，在多数基准线路上实现了门数的减少，平均优化率可达到26.88%。另外，实验中两种方法运行的时间均非常短（几秒以内），但本文算法运行时间还是普遍少于SABRE。由于空间限制，未在表1给出运行时间。

表1 映射算法比较结果

6 结束语

为降低量子线路映射过程插入的辅助量子门数，本文提出了一种基于量子比特权重系数的初始映射算法，并提出了一种基于双层展望窗口的启发式动态路由算法。实验结果验证了该方法可以快速生成量子线路映射结果，且较已有方法可以有效减少映射所需的辅助量子门数。