矿用带式输送机用永磁同步电机控制器研究

吴 康,杨京东,李大伟

(山西大同大学 煤炭工程学院, 山西 大同 037003)

近年来,我国能源呈现多元化的发展趋势,但煤炭仍占据主要地位,2022年全年能源消费总量中,煤炭消费量占56.2%,煤炭的生产效率不得不大幅度提高[1]. 矿用带式输送机因其远距离、持续性的优良特点,被广泛应用于采矿、冶金等大规模散装物料的采集运输中。作为原煤运输系统的生命线,其设备工作的稳定性和高效性尤其重要,在运行过程中一旦发生故障,不仅造成经济损失,甚至导致人员伤亡等事故。为此,有一套高效率、低能耗、持续性的驱动装置对于矿用带式输送机的稳定运行至关重要[2].

传统的异步电机依赖电网提供无功电流来建立旋转磁场,导致设备运行中系统的损耗相对较高,工作效率因数低[3].同时,后期设备机械装置维护困难且维修费用高。相较于传统的驱动装置,永磁同步电机采用内置永磁体励磁,不仅机身体积小、能量密度大,而且能在高负载率的情况下,不断提供较高的传动效率,同时功率因数也得到了极大地改善[4].起初,在永磁同步电机驱动系统中依靠机械式传感器对其转速、转子位置进行观测。但在煤矿井下恶劣的运行环境中,运用机械式传感器不能灵敏地进行观测,缩短了电机的使用寿命。为了尽可能地解决机械式位置传感器的缺点,理论推导发现在电机运行过程中,通过分析电压和电流参数便可推断出转子的位置和转速信息[5].

针对机械式传感器的弊端,基于脉振高频注入法,分析了信号激励下的PMSM数学模型,并设计了合理的转子位置信息提取方法,最后对传统的Luenberger状态观测器增加积分项以提高系统稳定性,最后在MATLAB仿真软件中进行了验证。

1 永磁同步电机的数学模型

三相PMSM是一个复杂的非线性系统,为了简化电机数学模型的建立过程,作出以下假设:电机铁芯的磁饱和不被考虑;不考虑电机的涡流损耗;不考虑电机的磁损耗并且没有阻尼绕组。在Ld=Lq的情况下开展研究。

同步旋转坐标系下,矿用永磁同步电机的数学模型:

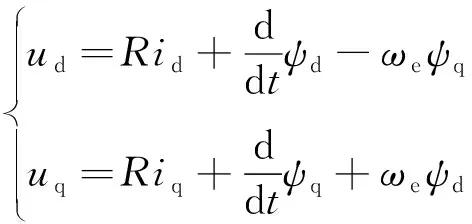
(1)

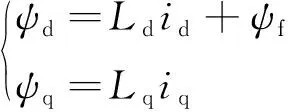
(2)

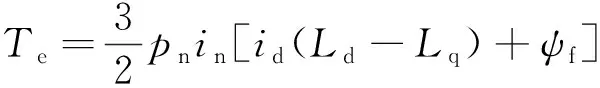
(3)

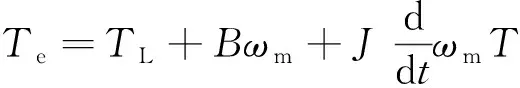
(4)

式中:ud、uq、id、iq为d-q轴电压和电流分量;R、Ld、Lq、Ψf为定子绕组电阻、d-q轴电感和永磁体磁链;Ψd、Ψq为d-q轴电磁分量;Te为电磁转矩;TL为负载转矩;ωe、ωm为定子角速度和机械角速度。

2 脉振高频注入法

目前,对于PMSM的全速域无速度传感器,尚无一种统一的方法实现全速范围的控制,多是划分为低速和中高速两种工况。目前,对中高速工况的研究较为成熟,通常采用滑膜观测器、MRAS(模型参考自适应)等,电机的运行信息可以从基波信号中获取。但在低速工况下,以上方法可利用的电压和电流信号较小,计算量较大且易发生误差,不容易获得转子位置和转速信息。针对此类问题,利用脉振高频信号注入法对带式输送机PMSM进行转子信息的提取,达到速度高性能控制的目的。

脉振高频注入法在电机零低速时具有较强的鲁棒性,注入的信号可以是旋转的,也可以是脉振的,但其原理均是把某一高频电流或电压信号,施加到基波模型的信号中,最后一同输入到电机的三相绕组里。本文主要利用脉振高频注入法对带式永磁同步电机实现高性能的控制。

2.1 PMSM在高频信号下的数学模型

由于注入的电压频率非常高,在高频激励的情况下,可将高频注入下的PMSM视为R-L负载。

(5)

(6)

则在转子同步旋转坐标系中,高频电流和电压之间关系为:

(7)

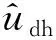
将(7)式用平均电感和电感差值的一半表示,则可写为:

(8)

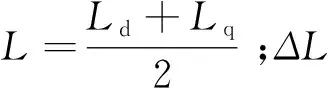
当高频余弦信号Umhcos(ωht)从输入端注入到d轴中时,便得到了同步旋转坐标系下的高频电压和电流方程:

(9)

由于电压方程组的电阻远小于电抗,因此在计算过程中可以将定子电阻忽略不计,最后联立上式可得到在旋转坐标系下的高频电流:

(10)

通过上式可以看出,如果d轴和q轴电感不同时,高频电流分量都与转子估计误差角Δθ有关;假设Δθ为零时,q轴的电流分流为零。所以脉振高频注入法通常是从PMSM输出端的q轴提取转子的位置和转速信息。因此需要算得q轴的电流响应分量:

(11)

2.2 转子位置估计

转子信息提取的实现过程见图1,通常是通过带通滤波器(BPF),提取所需要的固定频段内的电流信号;利用乘法器对此电流信号解调制,即通过数学运算处理输出的信号;通过低频滤波器(LPF)提取位置估算器所需的输入信号;经过位置估算器输出位置和速度信息。即:

图1 脉振高频电压注入法转子信息提取的实现过程图

(12)

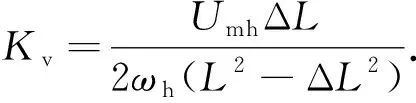
2.3 改进的龙贝格状态观测器设计

对于传统的Luenberger状态观测器,因其使用方便,选用常数作为反馈系数,使得转速改变时,观测器极易受到电机转速的影响,系统的性能显著降低。在不断的实验过程中,发现当在观测器系统中加入一个积分项时,转速输出的波形会更加平稳,震荡也比较少,系统性能有明显提高。改进的Luenberger状态观测器结构框图见图2,其中Ki是为了提高系统稳定性而增加的。

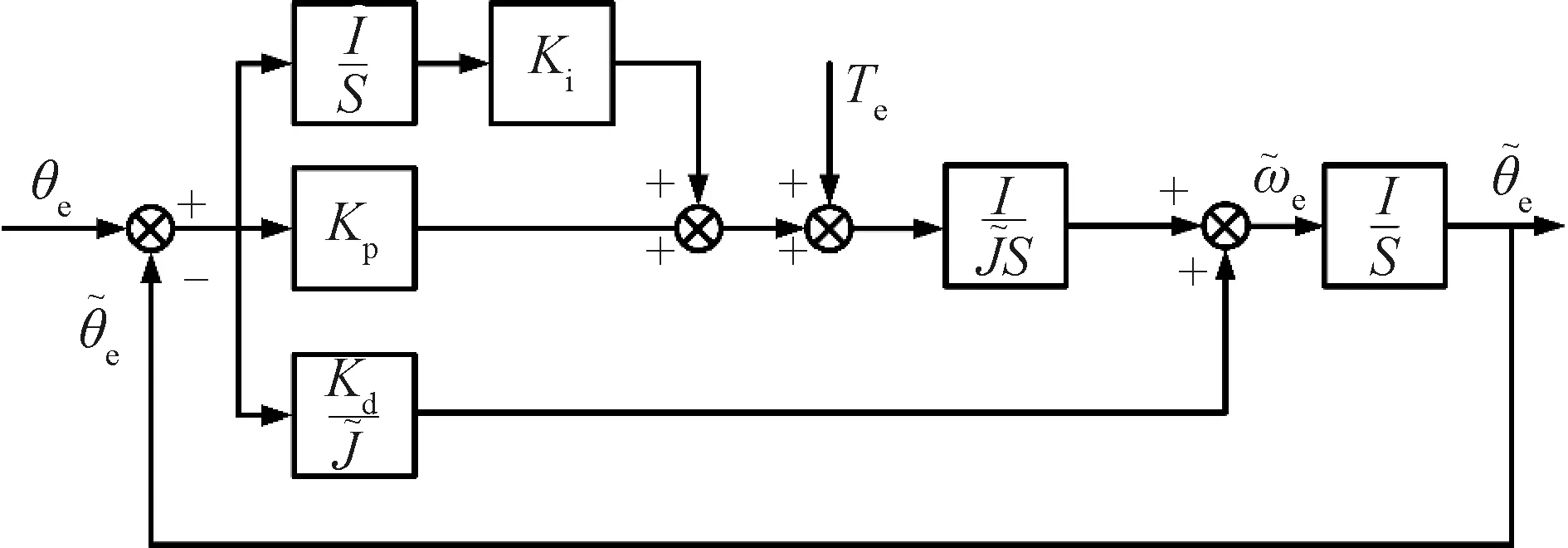
图2 改进的Luenberger状态观测器结构图

由图2可得出新的Luenberger状态观测器的估计精度表达式:

(13)

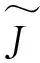
3 仿真与实验

3.1 实验模型与数据

为了分析以上理论过程,对矿用带式输送机在零低速阶段的现场运行工况进行模拟,并设计出矢量控制系统原理图,见图3. 电机参数见表1,且电机的仿真参数与实验参数相同。

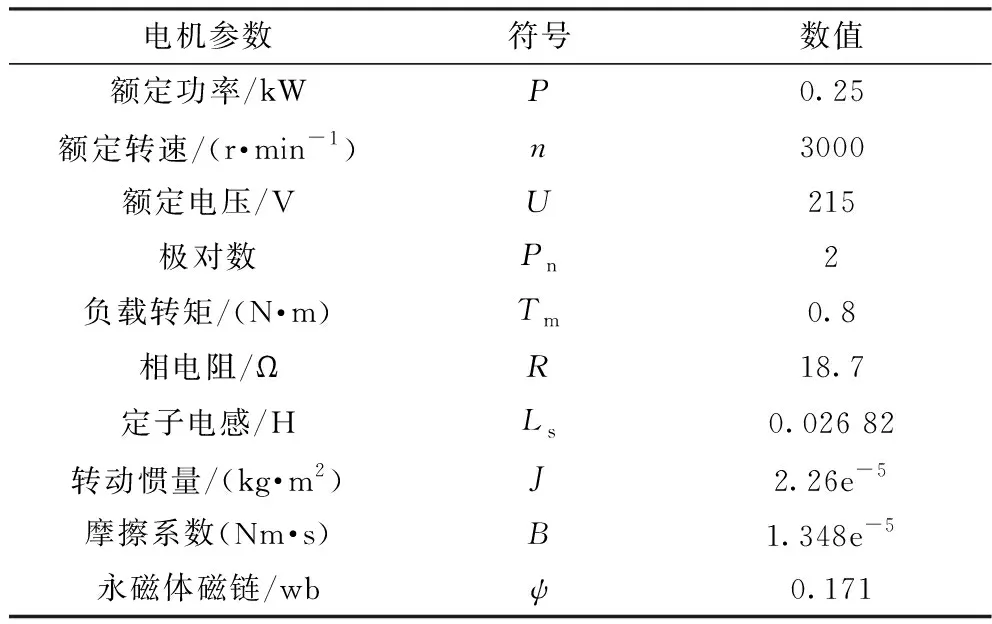
表1 电机参数表

图3 高频注入法矢量控制系统图

3.2 仿真分析

工况一:实际预设转速值100 r/min,时间设置为2 s,经过系统模拟运行,结果见图4.

图4 工况条件一下的仿真波形图

带式输送机在启动0.05 s后达到转速峰值(4(a));带式输送机转速的实际转速与估计转速基本重合(图4(b));电机初始启动时,电流突然增加到15 A,但在0.05 s后,电流趋于平稳的状态(4(c));初始时刻,d轴电流和q轴电流增大,在0.1 s后一直趋于稳定(图4(d)).

工况二:实际预设转速值100 r/min,时间设置为2 s,但在启动1 s后将转速突变为200 r/min,经过系统模拟运行,结果见图5.

由图5(a)可以看出,带式输送机初始启动0.05 s后达到峰值107 r/min,随后快速下降到预设值,并在1 s时,转速突变为200 r/min;由图5(b)可知实际转速和估计转速的曲线基本重合;图5(c)所示,电机在初始启动时,电流突增到峰值14 A,经过0.05 s,电流恢复正常;由于1 s时,转速突变为200 r/min电流发生剧烈波动,但立即趋于平稳。图5(d)所示为带式输送机PMSM的d轴电流和q轴电流波形,当转速突变为200 r/min时,q轴电流产生14 A的波动,而d轴电流无波动。

通过仿真实验可以看出,当带式输送机的转速突然发生变化时,实际转速和估计转速基本重合,在1 s初会有超调但最后可以稳定下来;说明输出电流和输出转矩能够很快响应负载转矩的变化。

4 结 语

为了满足带式输送机PMSM高性能的要求,在矢量控制的基础上,基于脉振高频注入法,设计了新的PMSM数学模型,并搭建了新的Luenberger状态观测器。最后在MATLAB中建立带式输送机脉振高频注入法的整体仿真,结果表明该方法能够减小信号的误差,具有良好的鲁棒性和稳态特性。