FY-3E微波湿度计发射前定标的非线性系数在星上定标中的适用性分析

王振占，肖雨伟，2，张升伟，何杰颖，谷松岩

1.中国科学院国家空间科学中心 中国科学院微波遥感技术重点实验室,北京 100190;

2.中国科学院大学,北京 100049;

3.国家卫星气象中心(国家空间天气监测预警中心) 中国气象局,北京 100081;

4.中国遥感卫星辐射测量和定标重点开放实验室 中国气象局,北京 100081;

5.许健民气象卫星创新中心,北京 100081;

1 引言

星载微波湿度计是用来测量地球表面和大气微波辐射的高灵敏度接收机，在系统设计上通常使其工作在系统响应的线性区域，可以通过两点定标来获取这个线性方程，进而实现对地观测数据的定标。然而在实际的微波湿度计系统中，微波器件的响应特性不可能做到理想的线性，必然会存在实际测量值偏离线性方程对应的理论值，这个偏移量通常称为系统的非线性误差，通常把在观测范围内最大偏离的亮温或者辐亮度称为湿度计的非线性误差。非线性误差是系统响应特性决定的，只有在准确获得系统的响应特性之后，才能确定系统的非线性误差。由于微波湿度计的观测物理量是辐亮度，或者亮温，因此通常非线性系数的单位也是辐亮度或者亮温，用亮温表示的系统非线性误差定义为（Wang等，2011）：

式中，TB0为目标（热真空实验中通常是指用于地物表面辐射模拟的变温定标源）的真实亮温，TBM为微波湿度计实际测量的亮温。当不考虑微波湿度计天线方向图影响的时候（实际情况天线方向图的影响需要考虑，这个过程称为天线方向图校正或者定标，这里目的是为了获得非线性系数，而在发射前定标中由于定标源紧邻天线，而且定标源后面足够大，所以天线方向图的影响可以忽略），星载微波湿度计测量的亮温TBM等于基于两点定标方法得到的天线温度TA（Weng等，2013）：

式中，a1、b1为定标方程的系数，VA为湿度计观测目标的输出电压。定标系数分别表示为

式中，VH、VC分别为热源电压和冷源电压，单位为伏特或计数值；TH、TC分别是热源和冷源的温度，单位为K。研究表明，两点定标得到的TBM并不能表征完整的星载微波湿度计系统，因为该系统还存在非线性成分，而这个非线性成分可以用二次项足够表示出来。微波湿度计的非线性误差与系统的工作状态（如仪器温度、接收机增益）、观测目标的动态范围有关，可以表示为如下形式：

u为湿度计系统的非线性系数，此外，

微波湿度计在轨运行过程中，虽然可以实时获得测量数据，但是TB0无法已知，因此在轨过程中的u是未知的，一般基于发射前定标的数据计算u。

星载微波湿度计发射前定标通常是指热真空定标，即在真空罐中利用液氮致冷的定标源作为冷源，工作在300 K 附近的常温源作为定标的热源，在95—335 K 变温的定标源，来计算微波湿度计在不同工作温度下的非线性系数（Saunders 等，1995；Mo，1996，2007；Kim 等，2014；He 等，2015；Wang 等，2019），确定星载微波湿度计在不同的工作环境下非线性系数u的变化。而在轨运行时星上定标所需非线性系数无法实时计算，是根据湿度计实际工作温度，对发射前热真空定标的非线性系数进行温度插值得到。

发射前定标和在轨星上定标的最大不同是冷源的使用：发射前定标的冷源通常控制在80—100 K（微波湿度计通常为95 K，后面以这个为例），而在轨星上定标的冷源是宇宙冷空背景温度2.7 K。从式（5）可知，非线性系数u的计算除了与输出电压相关，还与冷热源亮温值有关，所以采用热真空定标中的冷热源和变温源计算的非线性系数不一定适合在轨星上定标非线性修正。所以本文通过分析式（1）并在FY-3E 微波湿度计（MWHTSFY-3E）热真空试验过程中加入独立第3 个定标基准，来分析冷空条件下非线性系数的适用性。

2 研究方法或原理

虽然微波湿度计系统是一个线性系统，但是对于在较大亮温范围内还是存在较大的非线性，非线性的大小取决于湿度计系统的具体技术指标，由式（5）可知系统非线性误差ΔTB是关于VA的二次项，根据MWHTS 仪器性能和定标特点，因此我们可以假设湿度计系统响应是一个二次曲线，定标方程可以表示为（https：//trs.jpl.nasa.gov/handle/2014/14259［2021-07-08］）：

式中，a、b、c为定标系数。这种表达方式有助于直接确定输出电压与入射的天线温度之间的关系。从式（8）可以看出，微波湿度计的准确定标需3个有效观测点：(VC，TC)、(VM，TM)、(VH，TH)分别代表定标的低温、中间温度和高温点的电压和天线温度。利用这3个点，可以得到二次项系数为

b、c通过将3 个有效观测点代入式（8）解方程即可得到，这里不再列出。另外，结合两点定标公式（式（2））和微波湿度计非线性系数定义式（5）可得：

因此系数a还可以表示为

可以证明：对于湿度计定标测量数据的误差

精度要求来说，上述两个定义在二次曲线单侧（对称轴的一侧）相同的范围内的表达结果是相同的。结合式（10）和（11），可以得到：

式（14）表示当寻找到输出的电压位于冷源和热源电压的中间值时，非线性系数与冷热源输出电压无关，只与冷热源温度和中间电压对应的定标源的温度有关。式（14）的另外含义表明系统的非线性系数与冷热源的温度有关，发射前定标和发射后在轨定标的非线性系数是不同的。在冷空背景下，TC的值很小，对u的结果值作用几乎为零，当忽略TC的贡献，式（14）可变为

这个公式是非线性系数的一个近似表达式，可以用来估算在轨非线性系数的大小量级。非线性的大小取决于2TM和TH的相对大小，进而决定u的符号。当2TM=TH的时候，系统的非线性系数u近似为0。

另外式（12）直接提供了一种非线性系数的计算方法，通过3个定标点就可以计算对应范围的非线性系数。由于发射前热真空环境和在轨条件的差异，通常的发射前真空定标无法直接获取冷空定标的非线性系数。但是当增加一个中间亮温基准的时，就可以通过式（8）实时计算冷空背景TBC所对应的湿度计输出电压VBC，进而通过式（12）计算出在轨利用冷空作为定标低端的非线性系数。这种方法有望减小发射前热真空定标获得非线性的复杂度和成本。

3 发射前确定系统非线性系数的实验方案及其数据分析方法

3.1 实验方案

试验设计的方案如图1所示，真空罐内的热沉温度保持在100 K 左右（王振占 等，2013）。除了微波湿度计系统自带的热源（位于微波湿度计的环境温度）以外，试验还包括3 个定标源：变温源、冷源和验证源。变温源温度在95—335 K 范围变化，在试验中步进温度为15 K，用来模拟地球表面亮度温度变化；冷源的温度稳定在95 K 附近，使用液氮系统冷却；验证源不进行温控，只是采取被动包扎的方式，利用铂电阻实测其辐射体温度，最终的温度恒定在某个平衡温度。图1给出微波湿度计及定标源装配示意图，以天底位置（49，50 像元之间）为0 度参考，各定标源所在角度和观测位置如表1所示。

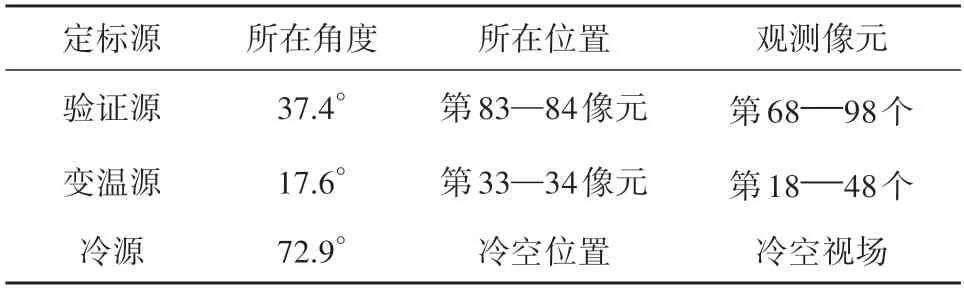
表1 各定标源所在角度和观测位置Table 1 The angle and observation position of each calibration source

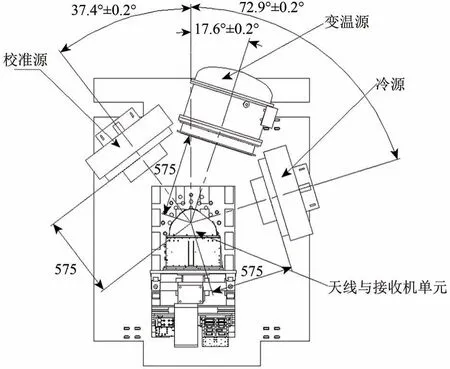
图1 热真空定标微波湿度计及定标源装配示意图Fig.1 Installing structure of MWHTS and three targets onboard the fixed test platform during T/V test

试验过程中，仪器温度的变化通过温控系统调整微波湿度计的底板温度在0 ℃—30 ℃变化范围来实现，工作温度设定为5 ℃、12 ℃、18 ℃、25 ℃。通过分析计算可以获取湿度计非线性系数及其误差、辐射灵敏度、线性度、辐射测量精度等主要技术指标，同时验证源可以独立验证非线性系数的定标结果。

3.2 冷空不变性及虚拟冷空观测的概念

MWHTS-FY-3E 采用宇宙背景温度作为低温参考点，结合卫星上微波湿度计自带的定标黑体，在每个扫描周期2.667 s内产生实时两点定标方程，对这个扫描周期内98 个对地观测数据进行定标，获得其对应的天线温度，进而经过天线方向图校正，获得场景亮温（Wang 等，2019）。对于MWHTS-FY-3E 的15 个通道，冷空的理论亮温见表2。这个亮温只与频率相关，与观测时间是无关的。因此对于一个系统指标确定的微波湿度计而言，其冷空亮温是不变的，我们称为冷空不变性。冷空不变性定标原理就是利用冷空的理论亮温是不随时间的变化而变化，在发射前利用这个亮温来模拟系统在轨输出电压，进而确定在轨定标所需要的非线性系数。冷空背景亮温可以表示为（Kramm和Mölders，2009）：

表2 MWHTS冷空理论亮温值Table 2 Cold space Theoretical brightness temperature of MWHTS

表3 通道1发射前和发射后非线性系数对于定标源亮温的敏感性比较Table 3 The comparison of sensitivity of nonlinear coefficients to the brightness temperature of the calibration source before and after launch in ch1

式中，Planck 常数h=6.626 × 10-34J · S；玻尔兹曼常数k=1.381×10-23J/K；光速c=2.9979×1010cm/s；波数υ为单位为cm-1；频率f单位Hz；Tcos=2.7 K。FY-3E 的MWHS 的4 个中心频率的冷空亮温如表1所示。

根据第2节的原理，在一个扫描周期内，利用3 个不同亮温点的观测数据就可以得到一条二次定标曲线，这个曲线就是当前周期内系统的真实响应曲线。利用这个曲线，可以外推得到湿度计在当前观测周期（由于辐射计系统增益和接收机噪声温度的变化，只能在一个定标周期内的外推才能有效）和动态范围内的任意一个亮温对应的观测电压，这个过程称为虚拟观测。基于这个虚拟观测概念，可以很容易产生当前扫描周期内冷空的虚拟观测电压。在虚拟过程中，冷空是实际在轨的冷空，是不变的，而其电压是虚拟的，是通过实测三点定标的方程实时外推的结果。实时三点定标曲线代表了当前扫描周期内稳定的响应特性，在其动态范围内都是成立的，因此利用这个曲线获得的当前扫描周期的冷空亮温和电压（TBC、VBC）也是成立的。用这对冷空亮温和电压，结合其他的定标源亮温及电压就可以计算在轨时的非线性系数以及其他性能参数。作为例子，图2给出1和10通道（89 GHz）在5 ℃时变温源从95—330 K变化（步长15 K）时观测4个定标源并外推冷空的电压比较。

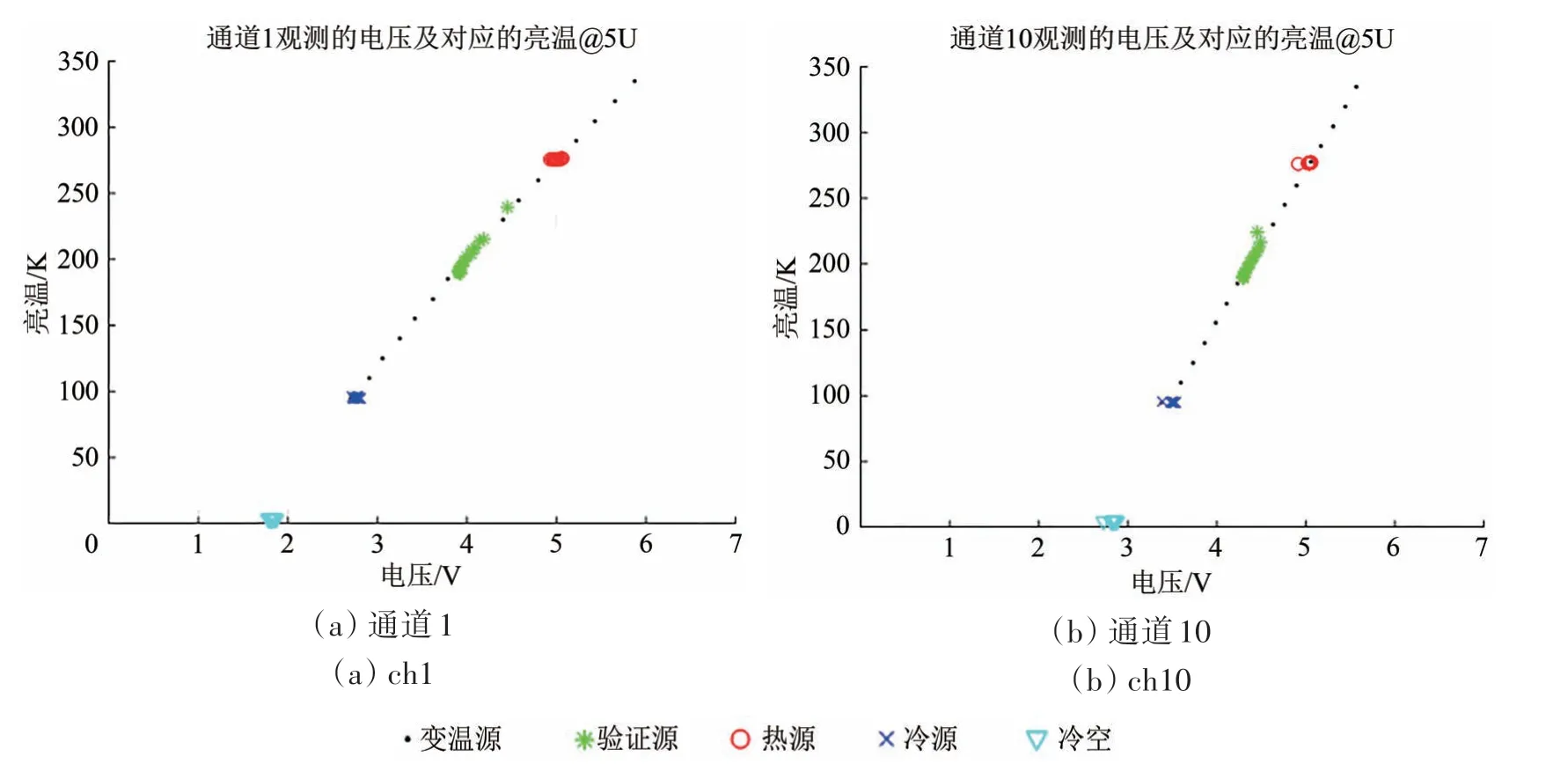
图2 通道1和10在5 ℃时观测4个定标源和外推冷空电压及其亮温的分布比较Fig.2 The voltage and brightness temperature distributions of four calibration sources observed and cold space extrapolated of ch1，10 at 5 ℃

在图2 中，每一个点都是200 包的平均值，代表了一个变温源温度点全部的有效观测。可以看出对于一个定标曲线，可以实时产生冷空的观测值。通道1输出的冷空电压值较为一致，而通道10的输出冷空电压在变温源95 K 时与其他温度点不一致，这个点是整个定标试验的第一个点，系统还没有完全处于稳定状态。图2中外推得到的冷空虚拟观测电压也是200包数据的平均值，它的准确度只受热源、验证源和冷源亮温准确度的影响。由于虚拟冷空电压是通过外推产生的，因此必须在一个扫描周期内的二次曲线外推得到的冷空电压才是有效的。从这个意义上说，发射前定标源起到基准传递的作用，获取准确的非线性系数的关键是各个定标源的准确度。

4 系统非线性系数的确定结果及分析

4.1 系统非线性系数的确定方法及其适用性分析

在获得冷空观测电压VBC后，结合宇宙背景亮温TBC和其他几个定标源的亮温及其电压，将定标源的偏差去除，就可以利用式（12）计算系统的非线性系数，进而分析不同冷源对于系统非线性系数的影响。为了直观，本文以亮温（单位K）作为辐射量的单位，非线性系数u的单位是“1/K”。

根据前面的分析，这里非线性系数的确定方法包括两种：

一种是常规定标方法确定的非线性系数，是指通过消除定标源偏差以后，计算变温源亮温和两点定标的亮温差，然后利用式（5）确定的非线性系数（Wang等，2019），包含了冷源、热源和变温源的亮温及其输出电压；另一种是利用式（15）的特殊点确定非线性系数的方法，包含冷源和热源，以及特殊点。本试验的特殊点可以来自验证源，或者变温源。详见下述分析。由于验证源的温度不进行控制，其输出电压刚好位于冷热源电压之间，因此特殊点不一定总是存在。参见图3通道1 的定标结果，图3（a）是电压，图3（b）是对应的亮度。在上图中，红色点线是冷热源中值的电压，其不但与变温源电压有交点，还与验证源电压有交点；蓝色点线是虚拟冷空和热源中值电压，其只与变温源有交点。因此验证源只能确定冷热源条件下的特殊点方法的非线性系数，而不能产生虚拟冷空的非线性系数。

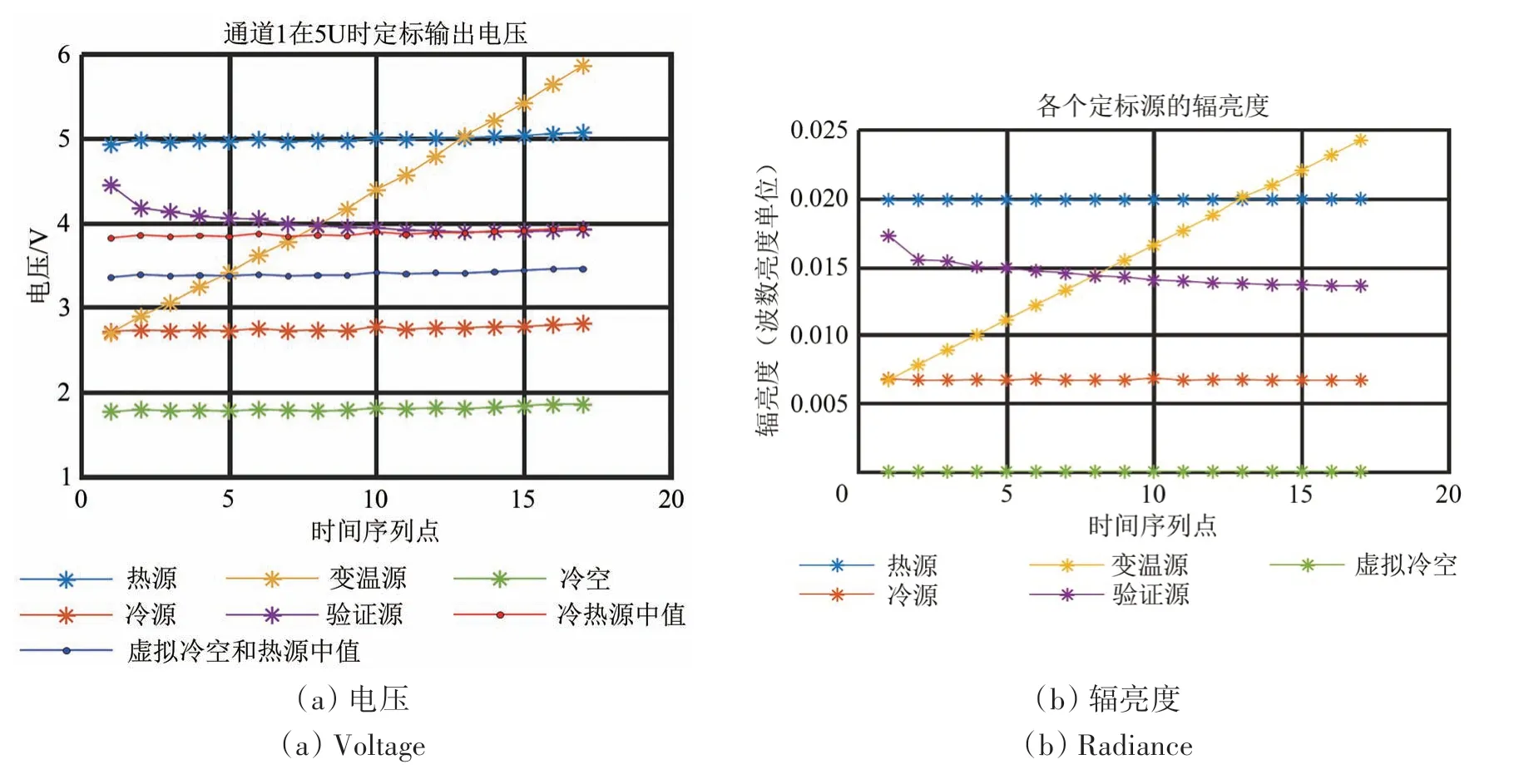
图3 在5 ℃升温循环（5U）通道1的各个定标源实测电压、辐亮度及虚拟冷空电压及其辐亮度在17个温度点（横轴为17个温度点对应的时间序列）的比较Fig.3 Comparison of the measured voltage，radiance of each calibration target，virtual cold space voltage and its radiance at 17 temperature points（Horizontal axis is the corresponding time series of 17 temperature points）of ch1 at 5U

为了比较使用冷端定标基准对非线性系数的影响，我们把使用冷源得到的非线性系数称为实测非线性系数，把使用虚拟冷空产生的非线性系数称为虚拟非线性系数。因此上述两系数的差异在于计算过程中使用的冷端定标源的不同。前者使用95 K 的定标黑体，后者使用虚拟冷空观测值及其亮温。

图4 给出通道1 在95 K 冷源定标和2.7 K 冷空定标时，采用常规定标和变温源特殊点定标4种情况下计算的实测非线性系数（对应图中冷源95 K）和虚拟非线性系数（对应图中虚拟冷空）的比较。对比图中四条折线可以看出：在实测的非线性系数和虚拟的非线性系数存在一定的差异，也就是说发射前采用95 K 冷源定标获得的非线性系数与在轨采用冷空的非线性系数是不同的。由于验证源在虚拟冷空条件下没有中间温度点存在，因此图中省略了特殊点方法获得的非线性系数的比较。其它各个通道的结果总体上类似，但差异的大小略有不同，由于篇幅关系，这里不再赘述。

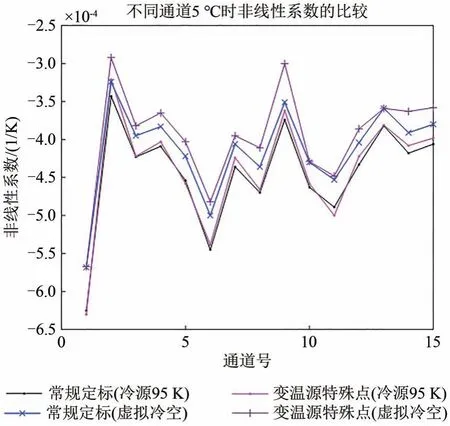
图4 通道1在95 K冷源定标和2.7 K冷空定标时，采用两种定标方法的非线性系数的比较（常规定标和变温源特殊点定标得到的实测非线性系数对应图中冷源95 K，虚拟非线性系数对应图中虚拟冷空）Fig.4 Comparison of nonlinear coefficients of the two calibration methods in 95 K cold target calibration and 2.7 K cold space calibration of ch1（The measured nonlinear coefficient obtained from the conventional calibration and the special point calibration of the earth target corresponds to the cold target 95 K and the virtual nonlinear coefficient corresponds to the virtual cold space in the figure）

下面以通道1为例，分析在不同非线性系数下不同方法定标误差之间的差异。图5（a）给出两种方法的实测非线性系数误差；图5（b）给出虚拟非线性系数的误差；图5（c）给出将常规定标方法得到的非线性系数用于在轨条件下的定标误差。从图5可以明显看出，传统的实测非线性定标对于发射前测量数据来讲误差很小，基本可以忽略（＜0.1 K）。如果冷源采用虚拟冷空，其定标误差就会略微增大，总体位于0.1—0.2 K。但是把传统的实测非线性系数代入虚拟冷空情况下的观测数据，其误差明显增大，整体达到±1 K，同时结果中仍然存在非线性成分，而且出现单调增加的趋势，这说明这个非线性系数不适用于在轨情况下非线性误差的校正。这是试验使用验证源验证传统方法的非线性系数适用性的目的。

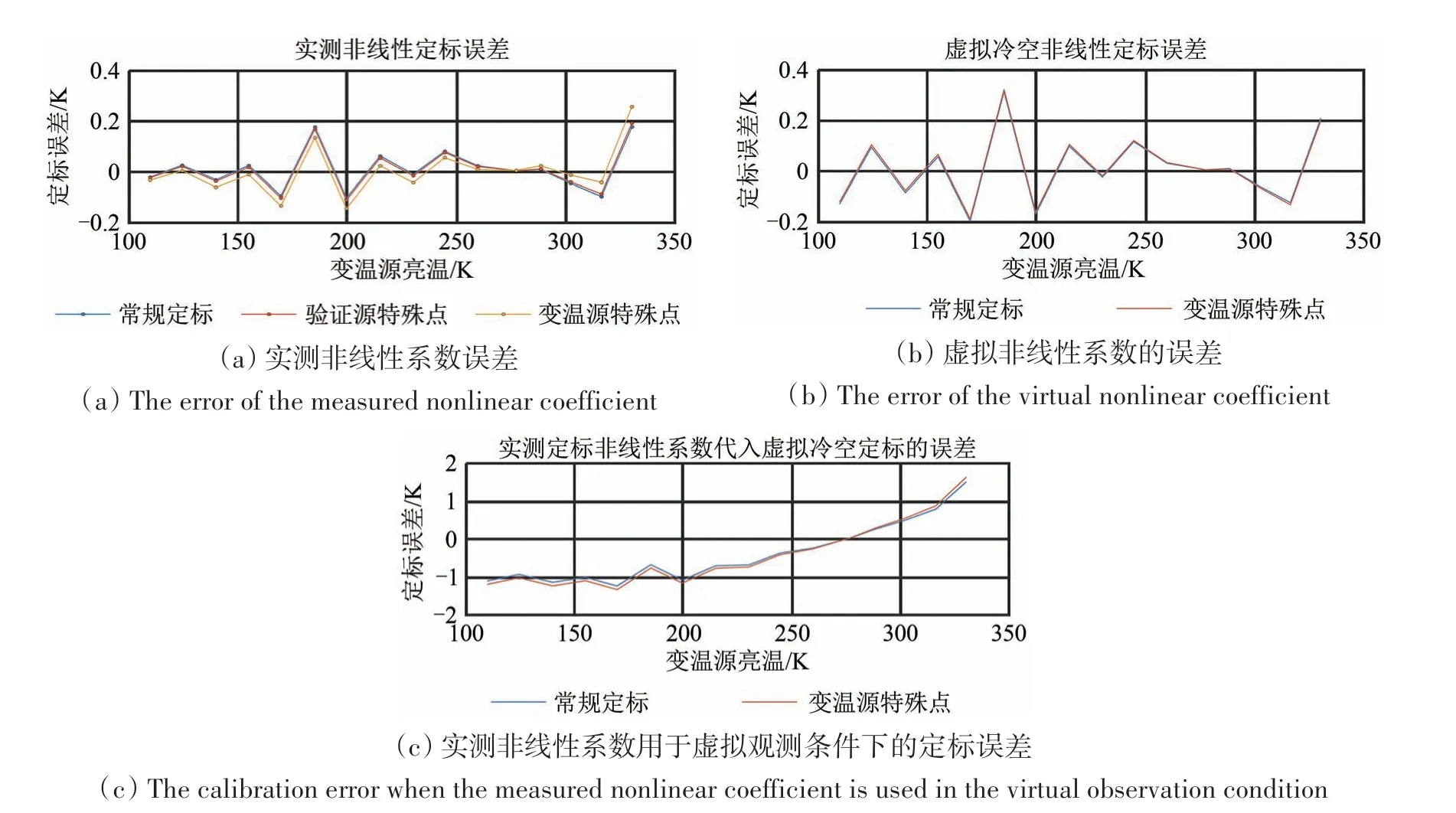
图5 不同非线性系数下不同方法定标误差之间差异的比较Fig.5 Comparison of calibration errors of different methods under different nonlinear coefficients

在图4中，每个通道的非线性系数是变温源在110—330 K 范围内16 个点非线性系数的平均值（去掉了第一个观测点，此时定标环境温度尚未稳定）。为了分析非线性系数变化产生的定标误差，图6给出两种情况下利用变温源的实测值和虚拟观测值获得的非线性系数均值及其标准差引起的定标误差随着变温源温度的变化。从图中可以看出，非线性系数波动导致的定标误差基本上在0.2 K 以内，发射前实测数据的定标误差略小于在轨的误差，除了330 K 情况下的误差较大，这与定标过程中的温度稳定性相关，这里不再深入分析。

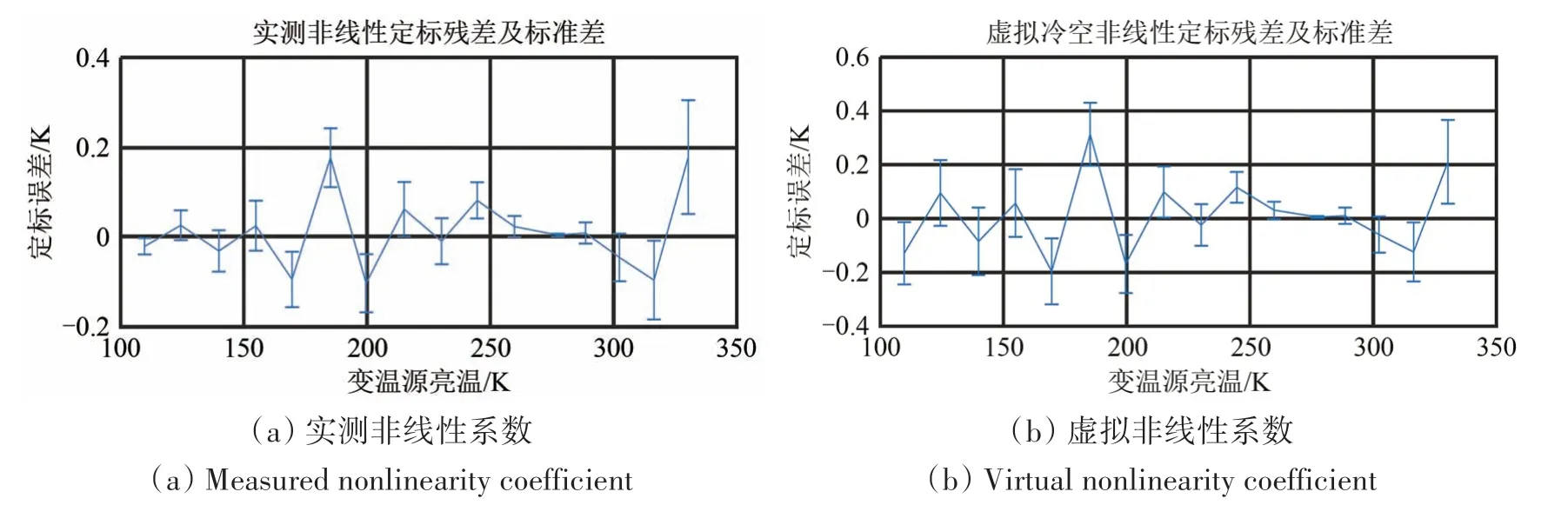
图6 在5 ℃升温循环（5U）通道1的非线性系数波动引起的定标误差随着变温源温度的变化Fig.6 The calibration error caused by nonlinearity coefficient fluctuation varies with the temperature of earth targets of ch1 at 5U

4.2 系统非线性系数的确定方法及其适用性分析

无论是以前利用冷热源和变温源获得的非线性系数，还是现在直接三点定标得到的非线性系数，定标源的亮温的准确性是这种方法使用的关键和难点，也是获得的u是否有效的决定性因素。我们知道，定标源亮温的准确度无法直接测量，只能通过部分测试结合计算得到。而定标源的发射率、反射率、温度准确度、温度梯度等因素是制约准确度的关键参数。

验证源由于处于温度平衡状态没有温度梯度，因此其偏差假设为零。冷源和热源的温度梯度是存在的。热真空罐的温度约100 K，接近冷源温度95 K，二者温差较小，但是真空罐中存在湿度计和定标热源等高温热辐射体，所以可能会导致冷源表面的温度梯度较大。热源处于微波湿度计内部，直接受到外界温度辐射的影响和间接受到由变温源升降温带来的环境温度变化的影响不大，因此温度梯度也较小。变温源是处于不断加热和制冷控制的，其温度梯度受到自身温度和外界环境温度之差的影响而不断变化，所以温度梯度最大的是变温源。

传统的方法不修正变温源的亮温，而是修正冷热源相对于变温源的冷热偏差。如果变温源自身亮温不存在非线性，那么两种方法是等价的。如果变温源自身亮温存在非线性，使用传统的非线性计算方法就会把这个非线性传递给湿度计的非线性。为了避免引入变温源的非线性问题，本文首先基于三点绝对定标，对变温源的亮温进行修正。图7 和图8 给出利用三点定标方法湿度计实测的变温源亮温相对于原始亮温（利用物理温度和发射率计算的亮温。本文使用的4个定标源的发射率＞0.9992，因此发射率导致的误差可以忽略，主要来自温度梯度的误差）的差（后者减去前者）。实测数据包括4 条测量曲线3 组AGC 下全部17 个点的温度采集数据，图中每个温度点的数据有180 组，一组数据包括200 包有效观测数据，包含了每个点定标过程中低频两个通道和高频两个通道单独定标的温度数据。图中结果也证明了变温源温度存在误差，而且这些误差是稳定的，与频率的相关性较小。同时从图中可以看出变温源亮温确实存在非线性，因此必须事先去除，以得到准确的接收机非线性。

图7 原始变温源亮温减去真实变温源亮温差的实测结果Fig.7 The actual result of the difference between the original earth target and the real earth target

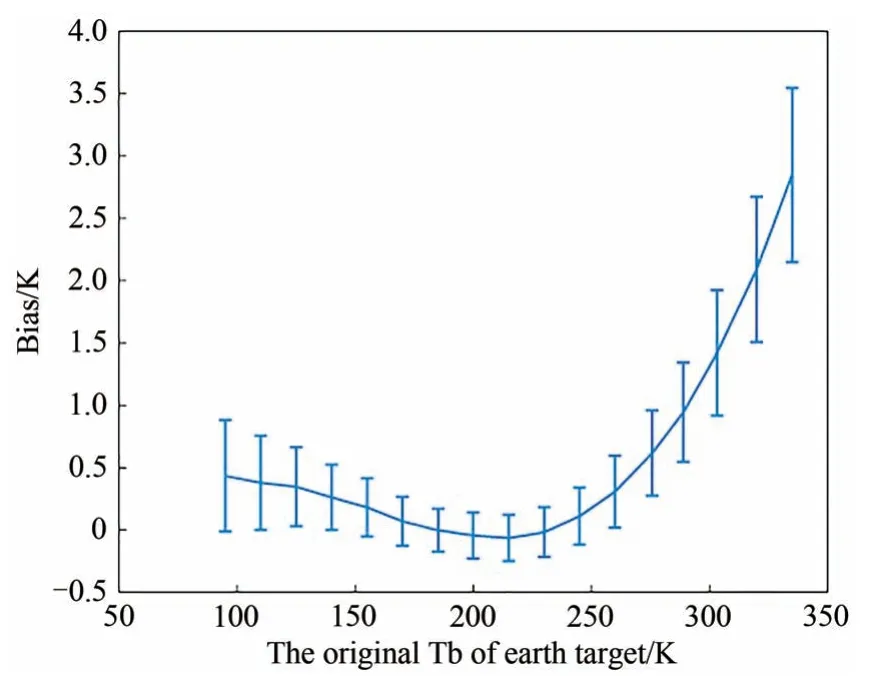
图8 原始变温源亮温减去真实变温源亮温差的统计结果Fig.8 The statistical result of the difference between the original earth target and the real earth target

下面简单分析非线性系数对于定标源的敏感性。根据式（14）可以得到：

从式（19）可以看出，非线性系数受到TM的影响只与TH和TC的范围有关，与观测的电压无关。表2 给出基于前文的观测数据得到的通道1 发射前和发射后非线性系数对于定标源亮温的敏感性。可见虚拟冷空情况下，对热源的敏感性增强，对冷空的敏感性减弱，对特殊点的敏感性变化较小。但是从数据的量级来看，特殊点的影响要远大于冷源和热源，因此在轨定标中，如果根据中间点的亮温来确定在轨非线性系数，则需要较高的亮温精度，否则可能对于非线性系数带来较大的误差。

5 结论

本文围绕微波湿度计系统非线性系数的确定方法及其适用性开展研究，通过首次在热真空定标中引入独立的验证源，基于微波湿度计在一个或多个定标周期内系统处于稳态响应的特性，提出了基于三点定标的方法来确定在轨非线性系数确定方法、虚拟冷空定标和虚拟观测的概念，同时提出了基于特殊点的非线性系数计算方法。在试验中，这个特殊点可以来自变温源，也可以来自验证源。文中的特殊点定标是三点定标的一个特例，其提供了一种计算非线性系数的特殊方法，其对于分析非线性系数的敏感性、简化定标过程，以及在轨定标中如何确定系统的非线性系数具有一定的理论和指导意义。

随后以FY-3E 的通道1 和10 为例，比较了各种方法的非线性系数结果，以及定标误差，并对传统发射前非线性系数的在轨应用误差进行了计算。

文章最后对于非线性系数对于定标源亮温的敏感性进行了计算，结果表明：在轨冷空的非线性系数敏感性相对发射前使用95 K 附近冷源的敏感性减弱，而在轨热源的敏感性相对增强。非线性系数对于特殊点（冷热源电压中值）亮温的敏感性要远大于冷源和热源，因此在轨定标中，如果根据中间点的亮温来确定在轨非线性系数，则这个中间点需要较高的亮温精度，否则可能对于非线性系数带来较大的误差。

志 谢感谢FY-3E 真空定标团队的辛苦工作并提供基础数据。