FY-3C微波湿度计-Ⅱ数据的再定标模型

王振占，肖雨伟，2，王可昕，2，张升伟

1.中国科学院国家空间科学中心 中国科学院微波遥感技术重点实验室,北京 100190;

2.中国科学院大学,北京 100049

1 引言

长期的、一致的微波探测仪观测数据集对全球气候监测、数值天气预报等具有重大的影响。自2008 年起，中国已经发射了风云三号（FY-3）A、B、C 和D 4 颗气象卫星，FY-3A 和FY-3B 上搭载的为微波湿度计MWHS（Microwave Humidity Sounder），FY-3C 和FY-3D 上搭载的为微波湿度计-II MWHTS（Microwave Humidity and Temperature Sounder），4 颗卫星的湿度计已积累了超过10 年的有效历史观测数据，利用这些数据，可以建立中国长期一致和稳定的大气湿度观测数据集（李娇阳 等，2019）。但是由于4 颗卫星上的4 台微波温度探测仪的系统响应特性和定标方法不尽相同，需要对这些有效历史观测数据进行一致性定标。

交叉定标法（常用星下点同步交叉定标法SNOs（Simultaneous Nadir Overpasses）、微波探测仪观测亮温减去基于辐射传输模型计算的模拟亮温OMB（Observation Minus Background brightness temperature statistics）、双差分法DD（Double Difference technique））等是建立长期一致观测数据集常用的方法。

目前，国内外已进行了一定的计算与研究。利用SNOs 对NOAA（National Oceanic Atmospheric Adminstration）系列卫星的MHS（Microwave Humidity Sounder）和AMSU-B（the Advanced Microwave Sounding Unit-B）进行一致性定标（John 等，2012）。利用Megha-Tropiques（Indo-French joint satellite）卫星上的Saphir（Sounder for Probing Vertical Profiles of Humidity）探测仪对NOAA-18、19 以及Metop-A（Meteorological Operational-A）上的湿度计进行交叉定标，并使用DD 方法对几台探测仪进行交叉定标（Jones 等，2013）。利用SEVIRI（Spinning Enhanced Visible and Infrared Imager）探测仪作为参考探测仪，对NOAA-18 和Metop-A 的MHS 进行长期一致的交叉定标（Buehler 等，2020）。利用OMB、DD 法对Metop-A、NOAA-19 上的MHS 进行交叉定标，使用NWP（Numerical Weather Prediction）模型进行亮温模拟（Saunders 等，2013）。利用自然目标（南极和热带海洋）、区域平均（60°S到60°N）、SNOs 3 种交叉定标方法对NOAA-15、16 的MHS 观测数据进行一致性定标（John 等，2013）。

SNOs 是直接建立定标辐射计观测亮温与参考辐射计亮温之间的函数关系，方法较为简单，但具有纬度局限性，而且本身容易受到参考辐射计亮温稳定性的影响，定标结果不容易区分两类辐射计数据各自的定标精度及其稳定性。OMB 和DD交叉定标法则是采用长时间序列数据的平均或者直方图进行分析，这种方法在一定程度上忽略了对辐射计系统的真实响应特性的分析，也没有考虑辐射传输模拟的正确性对于定标结果的影响。OMB 的方法是直接把背景场参数带入微波辐射传输模型，获得卫星同步观测的亮温，进而与卫星数据进行比较，从而校正定标偏差的过程，这种方法虽然受到背景场参数、辐射传输模型精度等影响，但它可以在全球尺度内进行大量匹配数据的比对，具有很好的统计稳定性，因此被广泛用于在轨数据的定标。

本文基于OMB 方法的累积，通过分析不同卫星的系统响应特性，结合辐射传输方程的计算，确定测量电压与亮温之间的系统响应特性，进一步分析系统响应的时空变化特征，从而利用模拟亮温随测量电压之间的函数关系建立湿度计定标模型。

2 研究方法或原理

2.1 微波辐射计特性基本原理

FY-3C 发射于2013 年9 月，运行轨道的高度为836 km（Gou 等，2015）。其上搭载的微波湿度计为第二代微波湿度计（MWHTS），包括15 个探测通道，均使用双边带接收机。

表1 给出了其15 个通道上下两个接收机的中心频点以及对应的极化方式，该极化方式随着扫描角θ的变化而变化。在θ为0°是极化是单一极化，其他角度都是混合极化。上下两个边带接收机接收辐射亮温的原理可表示为

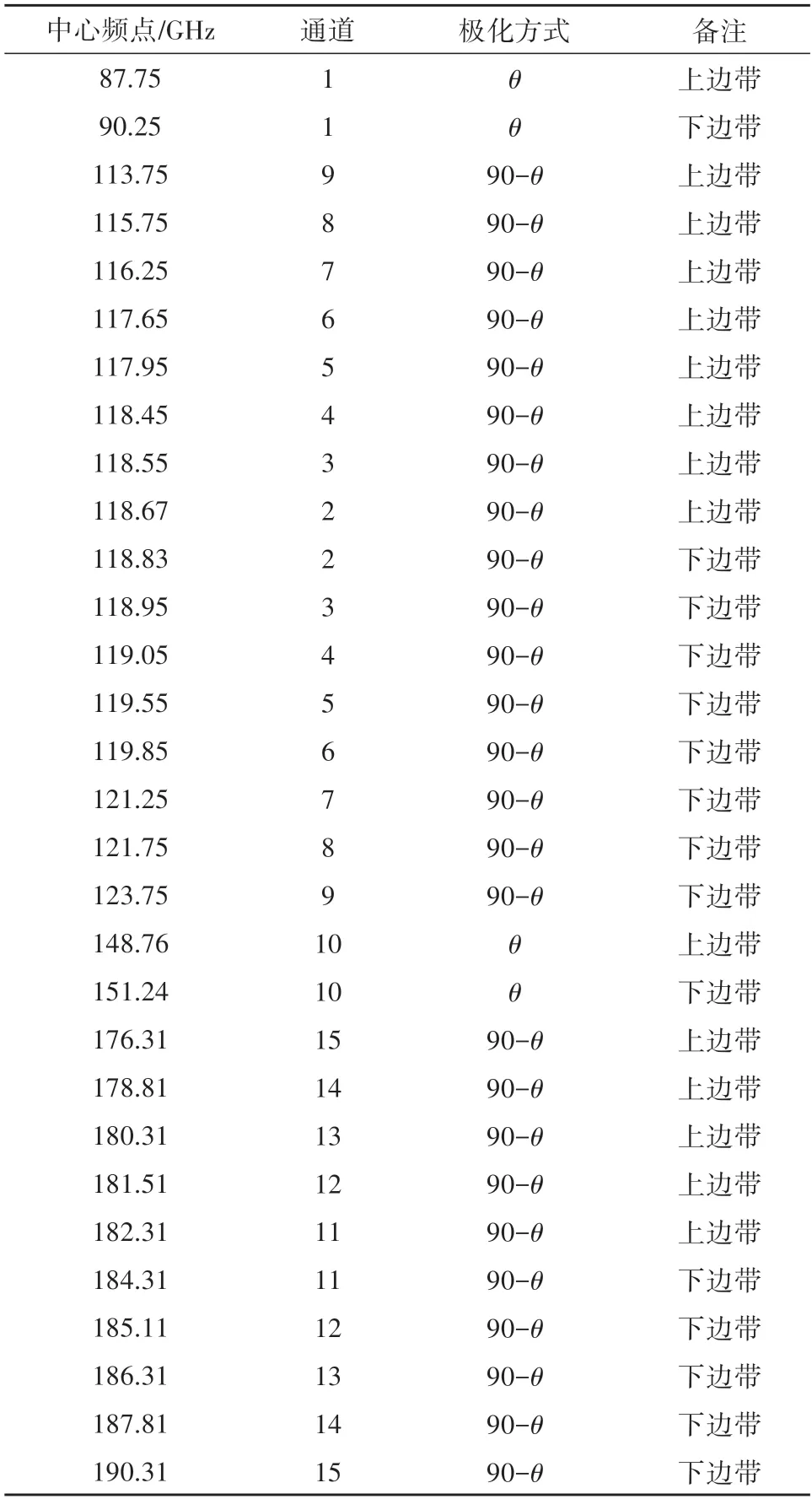
表1 MWHTS通道特点Table 1 Channel Characteristics of MWHTS

式中，fdown(v)和fup(v)为下边带和上边带的通道响应函数，vd1和vd2为下边带的频率边界，vu1和vu2为上边带的频率边界。P表示极化方式。

FY-3C 微波湿度计-II 采用两个反射面天线，在与卫星前进方向垂直的竖直面内进行交轨扫描，实现±53.35°扫描角的观测范围，其中，中心频率为89 GHz 的通道1 和中心频率为118.75 GHz 的通道2—9共用扫描天线，天线波束宽度约为2°；中心频率为150 GHz的通道10和中心频率为183.31 GHz的通道11—15共用扫描天线，天线波束宽度约为1.1°（Zhang 等，2014）。由于天线反射面在旋转，而馈源固定不动，因此微波湿度计接收的亮温是两个极化亮温的组合（Weng等，2003），即：

式中，θ是扫描角，当观测天底点时θ=0°。TBp和TBq表示两个正交极化的亮温。每个通道的亮温是这两个正交极化亮温的组合。因此，通道1 和10的亮温可表示为

其他通道的亮温为

2.2 微波湿度计的天线温度和亮温

微波湿度计计测量的天线温度TA可以表示为3种形式：

式中，VA、VH、VC分别为观测地球场景电压、热源电压和冷源电压，TH、TC分别是热源和冷源的温度，单位为K。u为非线性系数，单位为m2· Sr · cm-1· mW-1，通 常μ是接收 机温度的函数，在发射前通过热真空实验，测量不同仪器温度下的系统响应获得。在轨定标进行非线性修正时通过查表来获得实际工作温度下的μ值。当考虑天线方向图和天线辐射效率对于天线温度贡献的情况下，卫星接收的亮温TB,p可以简化为

式中，TA,p和TA,q表示表示同极化和交叉极化的天线温度，Tant表示天线的物理温度，a、b、c和d为系数。对于大气探测通道，通常只有一个极化方式，且这两种极化的天线温度非常接近，因此从实际数据处理的角度出发，上式可以进一步简化为

式（11）忽略了交叉极化贡献。把式（5）—（7）代入式（11）即可得到测量亮温的3种表达形式（为了简化篇幅这里从略），作为在轨定标偏差校正的基础。下文将以分析在轨数据特征及其与辐射传输计算偏差为基础，构建定标偏差校正模型—再定标模型。

2.3 FY-3C 微波湿度计-Ⅱ在轨数据及其OMB 结果分析

使用OMB 方法进行数据质量评价和定标误差分析主要是基于数据应用的考虑：一方面，由于微波辐射计的观测亮温至今没有绝对的参考基准，通过星上两点定标的结果可能存在一定的偏差。通过辐射传输模型和背景场计算的亮温具有统计稳定性，为卫星观测数据提供了可进行比较的参考基准，并且微波辐射传输模型计算的亮温作为参考基准可以实现不同载荷之间参考基准的一致性传递；另一方面，微波辐射计数据的应用是基于微波辐射传输模型的，利用OMB 方法得到的再定标数据和所使用的微波辐射传输模型之间是无偏的，可以直接用于基于同一模型的后续反演和同化应用，不需要再进行偏差修正。如果不使用当前微波辐射传输模型进行反演和同化，还是需要进行偏差校正的，这是因为不同微波辐射传输模型之间仍然存在偏差。总之，利用OMB 方法获得的再定标数据是稳定的，相对当前微波辐射传输模型来说是无偏的，相对其他微波辐射传输模型可能还存在稳定的偏差。

为了计算模拟背景亮温，这里使用MPM93（Liebe，1989；Liebe 等，1993）逐线计算大气吸收系数模型和FASTEM5（English和Hewison，1998；Liu 等，2011；Bormann 等，2012）的海面发射率模型。计算的输入背写数据来自ERA5的每小时的再分析数据集（Dee 等，2011）。在模拟两个正交极化不同扫描角亮温以后，根据式（2）—（4）计算对应通道的亮温。在积分过程中，通道响应函数设定为简单的矩形，上下边带的权重设定为0.5（王振占，2023）。后续计算将带入真实权重函数进行仿真。此处选取2013 年11 月到2016 年12 月卫星湿度计的L1级数据产品作为分析数据。

根据再定标前OMB 值随时间（扫描线）的变化结果，因为有些通道的变化具有共性，图1只展示了通道7、14的结果作为代表进行说明再定标前OMB 值随时间（扫描线）变化特征。从图1 可以看出，以通道14为代表的通道4、6、11、13、14，其再定标前OMB 值随时间变化趋势存在明显的波动，以通道7 为代表的其余通道总体OMB 值随时间呈现稳定的变化趋势。对于通道4、6、11、13、14 的OMB 值随时间变化波动的原因需要识别，并建立校正算法。

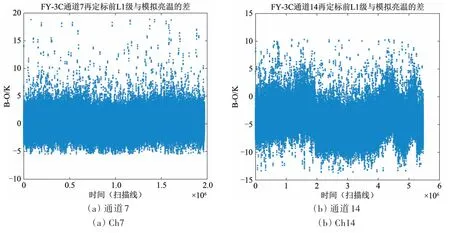
图1 通道7、14再定标前观测亮温与模拟亮温的差值Fig.1 Biases of observed and simulated brightness temperature before re-calibration in 7 and 14 channels

对这些数据进行进一步分析，发现引起偏差波动的主要原因是仪器温度的变化和接收机自动增益控制电压（AGC）的变化。图2展示了FY-3C微波湿度计在2013 年—2017 年期间接收机射频和中频温度的变化。可见在这个时间段，仪器温度有几个较为明显的跳变，为卫星系统操控的结果。部分通道（如13、14 通道）的偏差波动与仪器温度变化有一定的相关性。

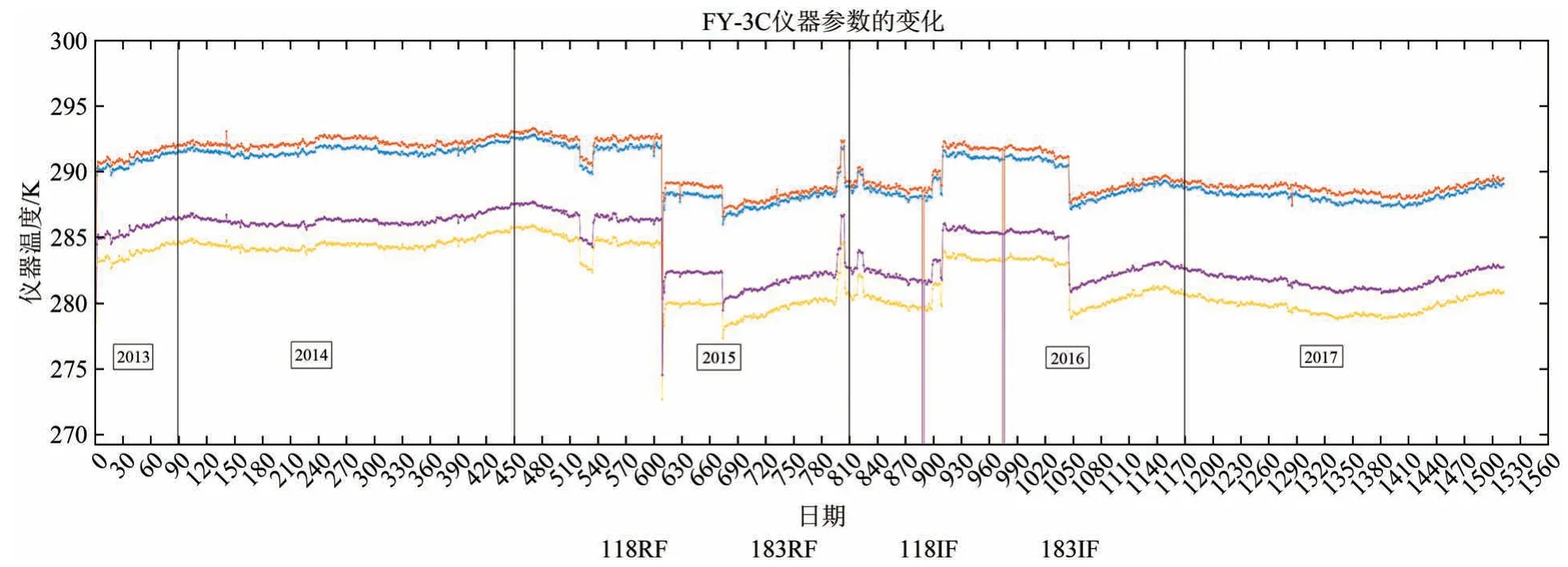
图2 2013年—2017年期间FY-3C微波湿度计仪器射频和中频温度的变化Fig.2 Time varying instrument RF and IF of FY-3C MWHTS during 2013—2017

15 个通道AGC 随着时间的变化如图3 所示。其中，通道6 的AGC 在2014 年—2015 年期间有一个大的跳变；对于其它通道，在发射初期（2013年9 月）和2015 年初期也都有一个较为明显的AGC变化；AGC 的变化与通道4 和5 偏差的跳变具有相关性。AGC 变化导致接收机非线性系数发生变化，而接收机的非线性系数又是仪器工作温度的函数，因此可以从仪器温度和定标源温度的变化分析定标偏差的变化原因，从而建立再定标算法。

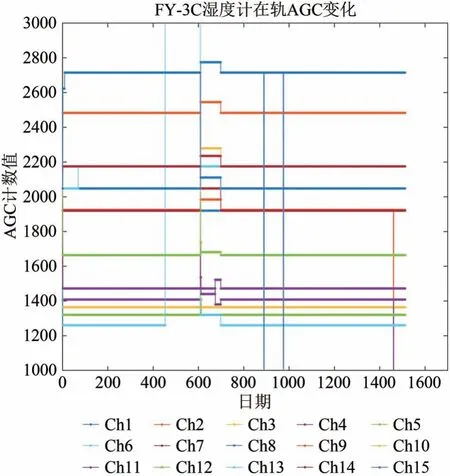
图3 2013年—2016年期间FY-3C微波湿度计在15个通道在轨AGC的变化Fig.3 Time varying AGC of MWHTS 15 channels during 2013-2017

3 再定标模型的建立及结果分析

3.1 再定标模型

结合式（10）和（11），定标偏差dTB为

式中，TBsim表示模拟亮温，TBobs表示观测亮温。当综合考虑冷热定标源误差、非线性误差以及天线温度的贡献时，可得到如下的表达形式：

式中，a，b，c，d，e，f，g，h为系数。如果忽略冷空亮温的变化，同时由于微波湿度计的天线和定标源处于相同的位置，其物理温度不是独立的，因此与热源温度合并考虑为一个影响因素，则式（13）可以简化为

式中，a，b，c为再定标方程的系数，用来解释由于热源温度、接收机温度变化产生的定标误差。

为了提高算法的稳定性和代表性，使用82 天的L1数据与ECMWF 的ERA5每小时的再分析数据集进行匹配。匹配标准：使用南北纬60°的晴空海面亮温，根据湿度计L1 产品中的地表类型为海洋进行筛选，晴空判断标准为积分液态水含量小于0.1，海面亮温大于275 K 以去除海冰的影响；时间上取观测轨道首尾时间上最为接近的EC 数据，时间匹配标准为小于±30 min，图4 为FY-3C 的L1级观测数据与ERA5每小时在分析数据集经过时间匹配后两者的时间差，由图4可以看出，经数据匹配后得到的数据级在时间差范围（±0.5 小时内）呈整体均匀分布，保证了卫星数据观测时间与ERA5 时间的无偏性；在全球经纬度的范围内，ERA5 数据是分辨率为0.25°×0.25°的网格形式，将L1 级数据的经纬度对应到此网格中，经纬度的匹配标准小于±0.125°。

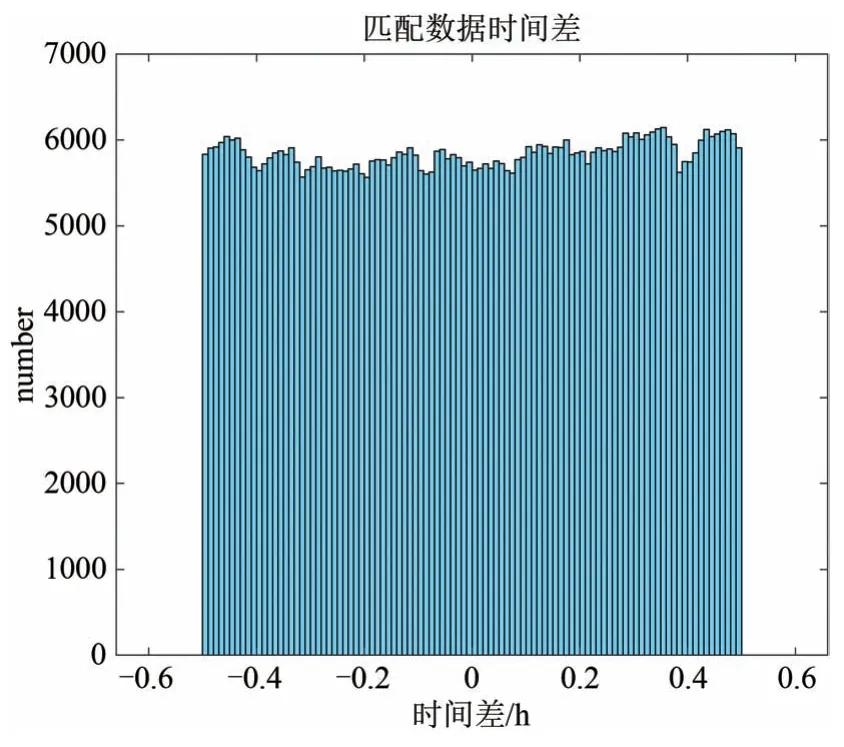
图4 FY-3C L1级观测数据与ERA5每小时再分析数据集进行时间匹配后两者的时间差Fig.4 The time difference between L1 level observed brightness temperature and ERA5 hourly reanalysis data set after time matching

3.2 再定标结果分析

对匹配好的数据进行分析，发现落在一个ERA 网格通常有1—4 次观测点，为计算数据的均匀性和有效性，选择了在一个网格内有3—4 次观测点作为基准观测数据，并要求这些观测数据之间的标准差小于0.3 K。利用这些匹配的网格点的ERAS 数据进行模拟亮温计算产生最终的再定标算法系数。经第2节分析，AGC的变化可能对再定标结果造成影响，同时也计算了输入数据在不同AGC下的定标系数。

图5 为再定标前后部分通道（通道7 和14）观测亮温和模拟亮温之间的定标偏差和标准差随热源温度和时间的变化示意图，其中图5（a）（b）中“产品”图标代表着再定标前OMB 值及其标准差，“区分”图标代表着在不同AGC 下计算的多组再定标系数得到的再定标偏差和标准差，“不区分”图标代表着所有数据计算的一组再定标系数得到的再定标偏差和标准差；图5（a）（b）分别为通道7和通道14 再定标前后OMB 值随热源温度的变化、再定标前后OMB 值随时间（天数）的变化及再定标前后OMB值的标准差随时间（天数）的变化。

图5 再定标前后通道7、14观测亮温和模拟亮温之间的定标偏差、标准差随热源温度和时间的变化Fig.5 The variation of calibration deviation and standard deviation of observed and simulated brightness temperature before and after re-calibration in ch7 and ch14

由图5（a）中间图可以看出，对于通道7，区分和不区分AGC 下再定标结果均较好，OMB 值的大小和波动都得到校正，但是区分AGC 的再定标结果优于不区分AGC 通道6、11、12 结果与通道7的结果相似，在区分AGC 的条件下，再定标后的偏差小于不区分AGC 的定标偏差，并且偏差的波动得到更好的改善，限于篇幅原因，结果图不再列出。因此，对于通道6、7、11、12，这些通道AGC 的变化对定标结果有一定的影响，在定标系数中需要考虑AGC的影响。

由图5（b）中图可以看出，对于通道14，区分和不区分AGC 下计算的定标结果均较好，再定标后的偏差大小和波动都得到改善，两种情况下计算的结果基本没有差别。通道1、13、14、15再定标结果与通道14 结果相似；通道2、3、8、9、10 在不区分AGC 下的再定标结果略好，限于篇幅原因，这些通道的结果图不再列出。因此，对于受AGC 的影响不明显的通道，选择不区分AGC 下的定标系数进行再定标。

对于通道4、5，再定标后的OMB 值大小得到校正，但是OMB 值仍然存在波动，图6 为再定标前后通道4观测亮温和模拟亮温之间的定标偏差和标准差随热源温度和时间的变化示意图。从图6中的中间时间变化图可以看出，无论区分和不区分AGC 的定标结果，在30—50 对应的时间范围，OMB 值仍然存在相对较大的波动。通过分析原因发现，这可能是在星上定标时使用的非线性系数不合适。L1 级观测亮温是L0 级原始观测数据经过星上定标得到的，在星上定标过程中需要进行非线性修正，而在波动处该通道的中频温度发生变化，非线性系数u对中频温度的变化不敏感，导致在该处进行星上定标时非线性修正量不准确，因此导致L1 级观测数据存在人为误差，进而造成的此处波动，后续会对非线性系数进行进一步讨论。通道5 的在第27—30 时间段OMB 同样值存在相对较大的波动，波动原因与通道4一致，此处不进行详细分析。

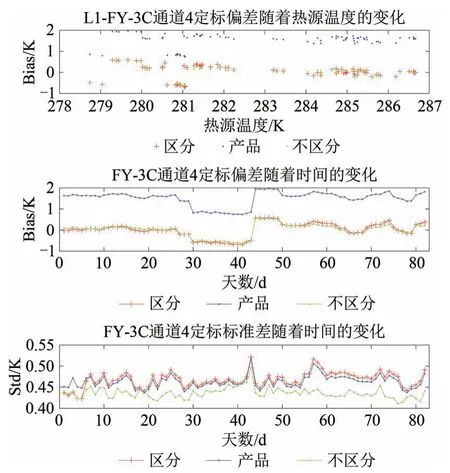
图6 再定标后通道4观测亮温和模拟亮温之间的定标偏差、标准差随热源温度和时间的变化Fig.6 The variation of calibration deviation and standard deviation of observed and simulated brightness temperature before and after re-calibration in ch4

虽然通道4、5 再定标结果不是很理想，但其余通道通过考虑定标源温度、仪器温度和AGC 的变化，可以实现OMB 偏差的大幅改善，实现了数据的稳定定标。为分析该定标模型的有效性，4、6、7、11、12 通道采用L1 数据区分AGC 的再定标系数；其他通道采用L1 数据不区分AGC 的系数。再定标系数见表2。

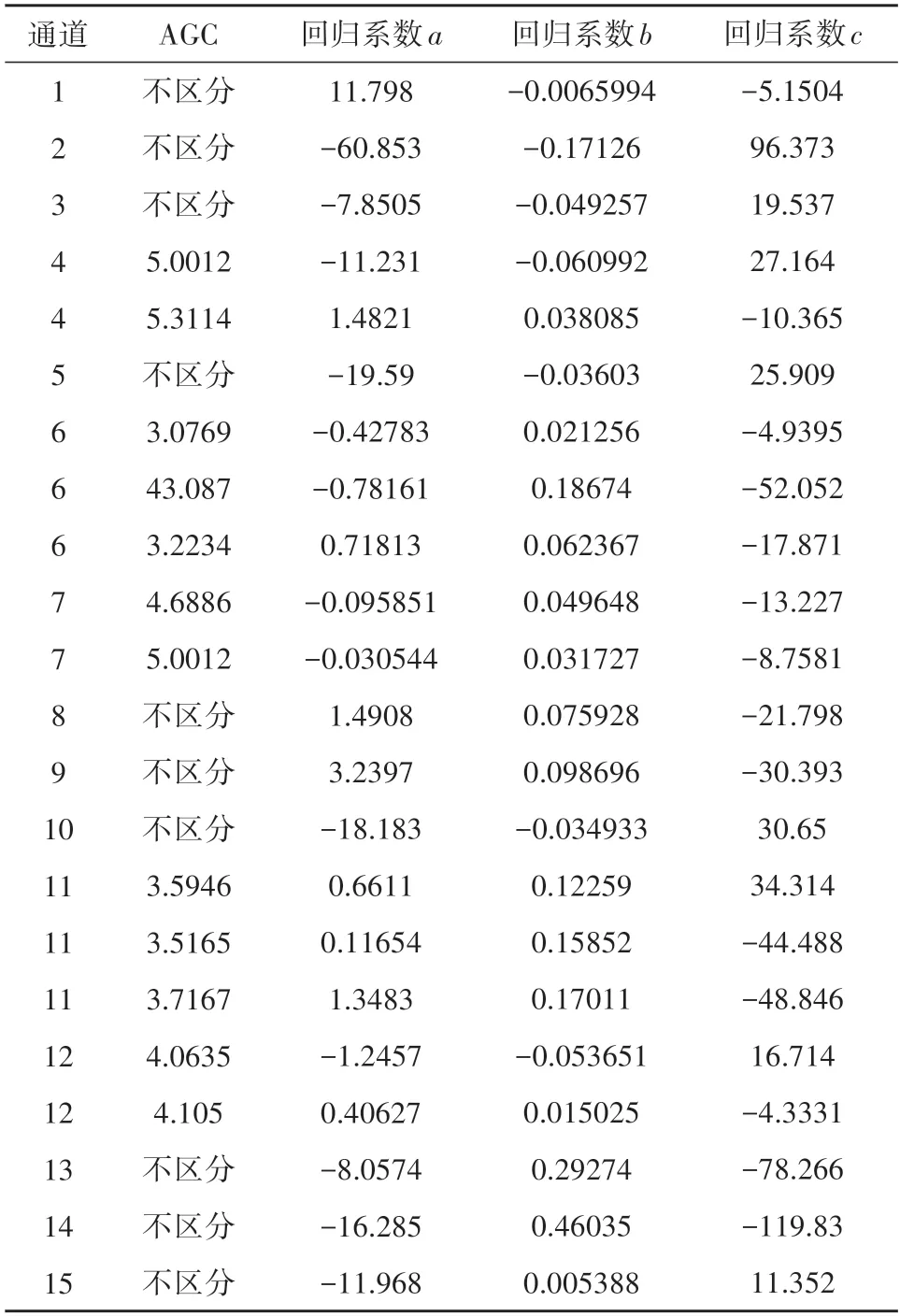
表2 FY-3C MWHTS各通道再定标模型系数Table 2 The parameters of re-calibration processing of FY-3C MWHTS

图7 为通道7、14 再定标后OMB 偏差随时间（扫描线）的变化。由图7（b）可以看出，通道14偏差波动得到改善。

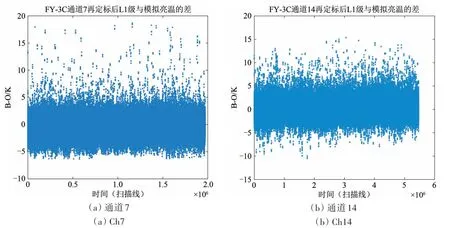
图7 通道7、14再定标后观测亮温与模拟亮温的结果比较Fig.7 Comparison of observed and simulated brightness temperature after recalibration in ch7 and ch14

为了定标结果的稳定性，我们下面主要分析算法的残差特性。图8 为通道7、14 再定标前后的OMB 偏差直方图，从图8 可以看出，定标前后的偏差直方图存在明显差异：如通道7虽然呈现一定的正态分布，但是它们明显存在两个分布特征，直方图的分布至少是两个状态的叠加，这对应于这些通道AGC 的变化；通道14 定标之前明显不是正态分布，存在两个峰值。而经过再定标以后，通道7、14 的OMB 值呈现理想的正态分布，证明了该方法的有效性。对于其他通道，OMB 值也都呈现理想的正态分布，这里不在一一列出。

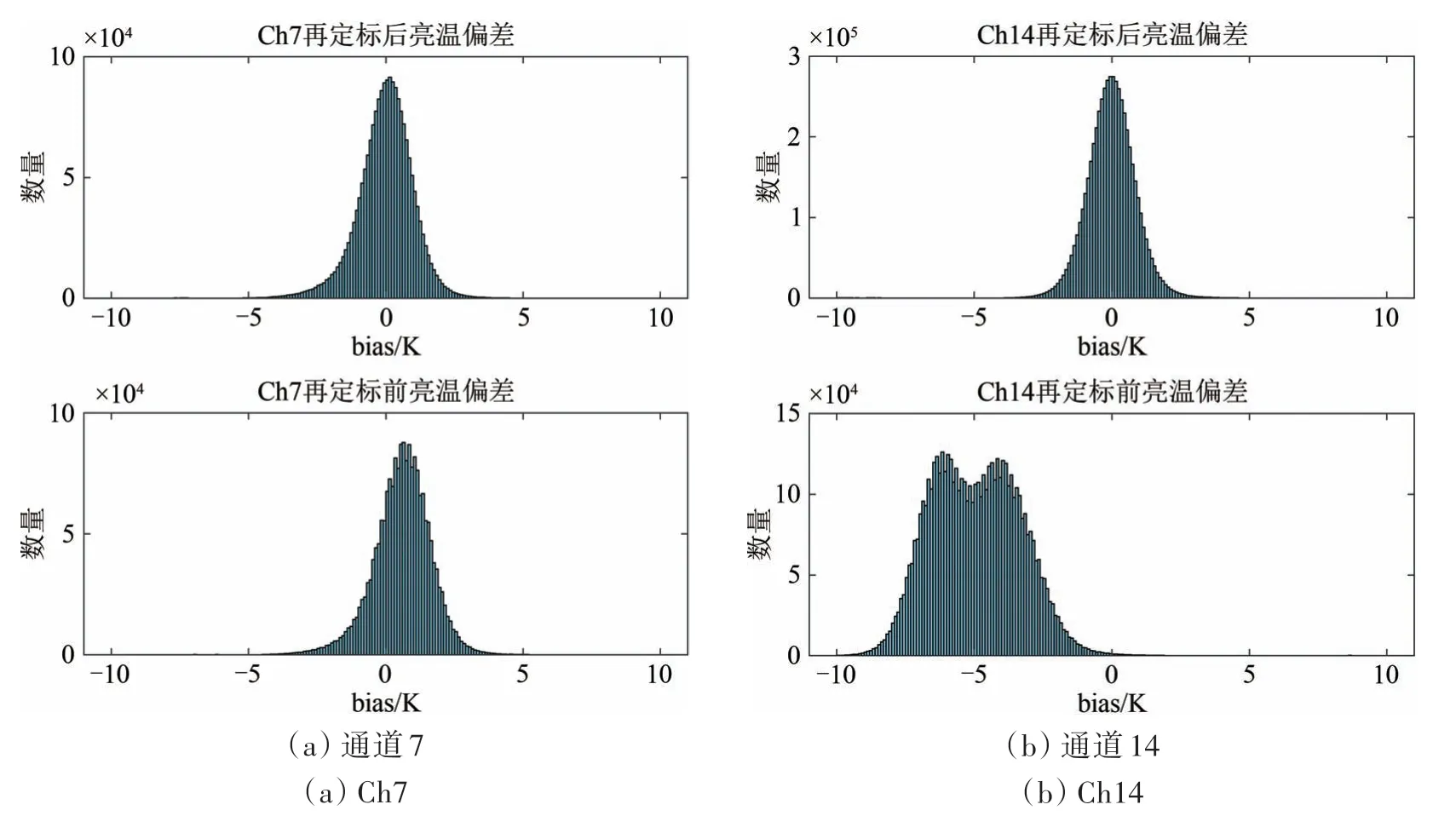
图8 匹配观测点为3—4次时，通道7、14再定标前后的OMB偏差直方图比较Fig.8 Comparison of the OMB bias histogram before and after re-calibration processing in ch7 and ch14

4 再定标结果验证及分析

4.1 利用同时间样本中的其他数据进行验证

下面利用同一网格内匹配点只有1—2 次的数据进行验证，以判断算法系数是否可以用于一般的匹配情况。一般情况中0.25°网格内的不同匹配数据可能包含位置差异、大气条件差异和计算误差等，而且数据之间的离散度越大，说明这些差异越大。因此，可以利用这些数据验证再定标算法系数是不是产生稳定的效果。由于匹配点1—2 个的情况下无法判读像元内数据的稳定性，不能有效判断降水等在像元内是否存在，所以这些数据的离散程度略微增大。图9 为当匹配观测点为1—2次时通道7、14再定标前后OMB 偏差直方图。由图9 可以看出虽然这两个通道的离散度略微增大，但是明显看出定标系数对于这些通道是完全适用的，很好地实现了定标偏差和异常数据的校正，对于其他通道特征与通道7、14相似。

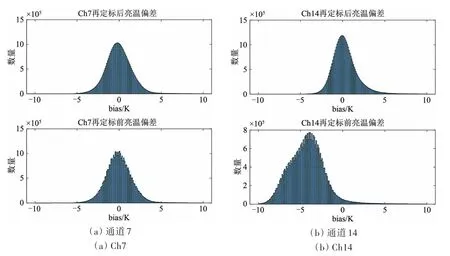
图9 匹配观测点为1—2次时通道7、14再定标前后OMB偏差直方图比较Fig.9 Comparison of the OMB bias histogram before and after re-calibration processing in ch7 and ch14

4.2 利用未覆盖时间段的数据进行验证

为了检验定标结果，进一步选择其他独立的数据进行验证。在此，选择2017 年—2019年期间60天的数据进行算法鲁棒性的验证。图10（a）为通道7再定标前后观测亮温与模拟亮温之间的偏差和标准差随天数的变化，通道7 再定标前OMB 值本身很小，再定标完之后OMB 值相对来说变化不大。图10（b）为通道14 再定标前后观测亮温与模拟亮温之间的偏差和标准差随天数的变化，可以看出利用再定标系数，OMB 值变小，波动也得到改善。对于其他通道的再定标模型也都很好地实现了定标偏差的校正，使得定标偏差稳定，在所分析的跨度3 年的60 天范围内，定标偏差的波动较小。图11部分通道经过再定标之后的直方图，这两个通道都呈现理想的正态分布，其他通道也是如此，再次证明了该方法的有效性。

图10 利用2017年—2019年期间60天数据进行再定标的验证结果Fig.10 Validated results of the re-calibration processing using sixty days’ data during 2017—2019

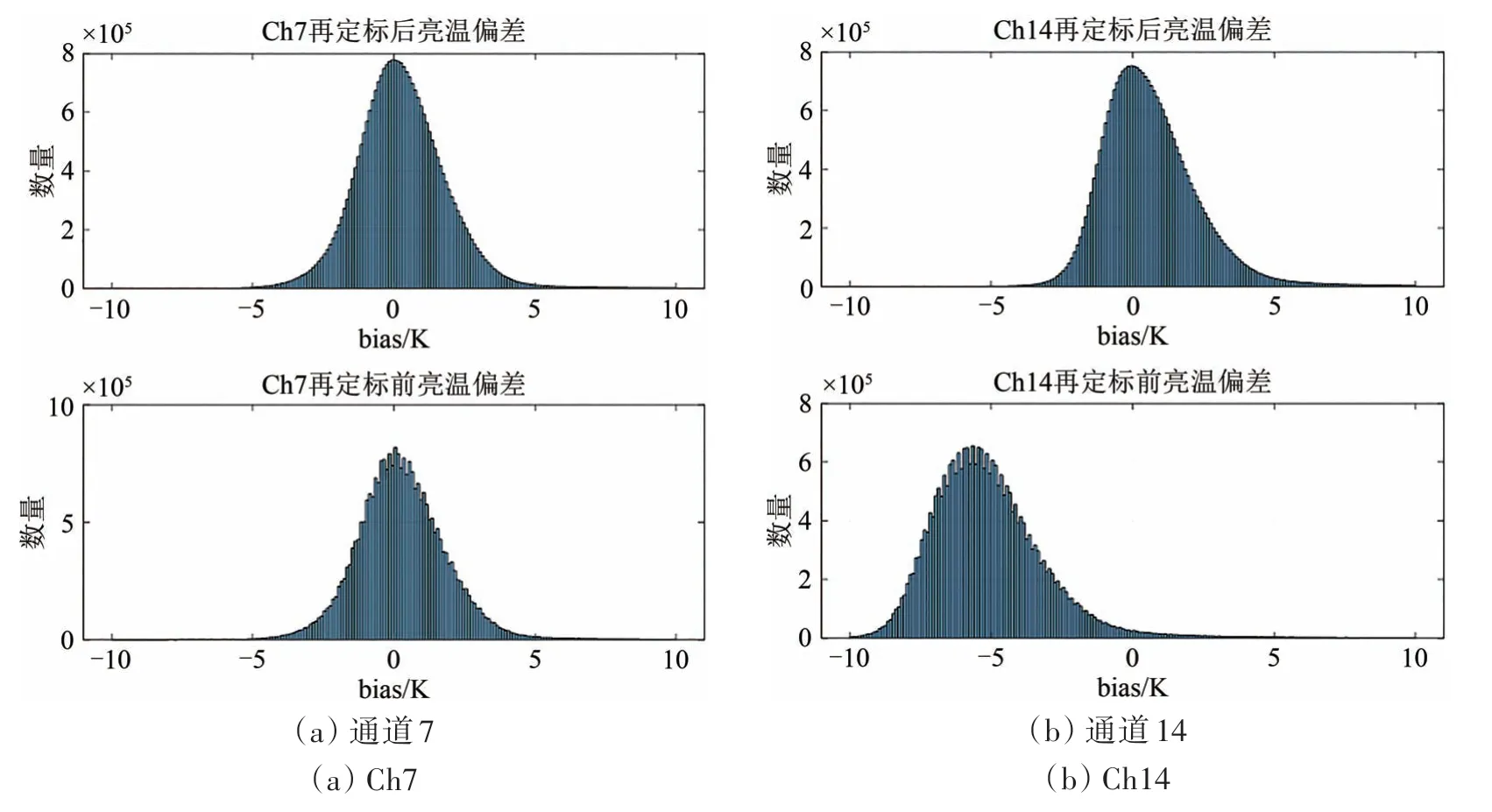
图11 利用2017年—2019年期间60天数据进行再定标前后OMB偏差直方图比较Fig.11 Comparison of the OMB bias histogram before and after recalibration processing using sixty days’ data during 2017—2019

4.3 定标残差的分布特性统计

由于微波湿度计采用交轨扫描的形式进行观测，因此在98 个观测位置上的偏差是否存在位置相关性一致都是大家关心的问题（Goldberg 等，2001；Tian 等，2018）。这里对于再定标前后观测亮温与模拟亮温之间的偏差和标准差的分布特性进行统计。图12 为FY-3C 的MWHTS 的所有通道再定标后观测亮温和模拟亮温之间的偏差随扫描点的变化趋势。在选取数据时，选取了3—4 次观测点进行了模型的建立，位于边缘扫描点的数据个数不满足条件，造成了边缘位置的匹配的统计数据缺失。由图12 可以看出，对于C 星微波湿度计的所有通道，第16—88 个扫描点的偏差得到了较好的修正，但再定标前后的偏差都随着扫描点的变化而变化，具体原因会在之后的工作中进行分析。图13 为15 个通道再定标前后观测亮温和模拟亮温之间的标准差随扫描点的变化趋势，再定标前后OMB的标准差变化很小，趋势也不变。

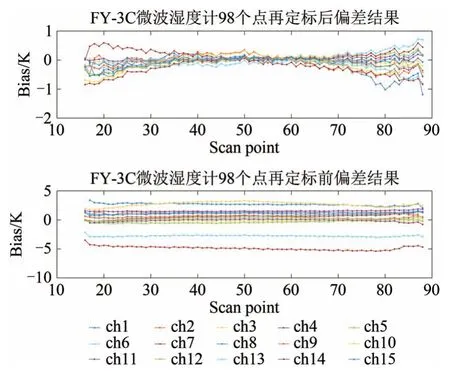
图12 匹配观测点为3—4次时，所有通道再定标前后OMB偏差随扫描点的变化Fig.12 Varying of OMB bias with scanning point before and after recalibration of all channels using 3—4 observed points

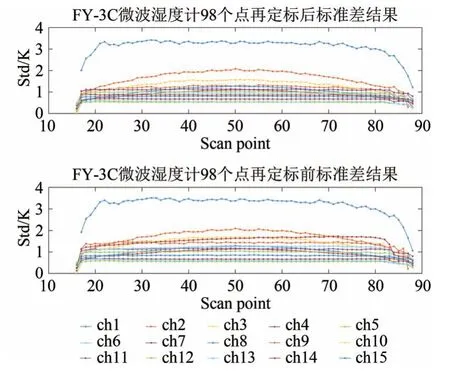
图13 匹配观测点为3—4次时，所有通道再定标前后OMB标准差随扫描点的变化Fig.13 Varying of OMB std with scanning point before and after recalibration of all channels using 3—4 observed points

5 结论

本文利用微波辐射计通道特性，对FY-3C 湿度计历史数据进行再定标分析。基于OMB 方法，直接利用辐射计系统响应特性，结合辐射传输方程来进行定标偏差分析，在考虑模拟和观测数据时空匹配的有效性时，不但依赖其统计特性的稳定性，而且在2.667 s 定标周期内的需要通过湿度计实时观测的电压数据来评判时空匹配的有效性。所以本文基于对不同卫星的非线性参数、热源温度和电压以及匹配点的数据电压特性的综合考虑，建立新型的历史数据再定标算法。再定标后的OMB 值明显减小，在统计特征上，OMB 的值基本符合正态分布特性。从2013 年—2017 年4 年期间选出代表性的82 天数据偏差变化来看，通道4 和13的最大偏差不超过1 K；其他通道再定标后的观测亮温和模拟亮温的最大偏差不超过0.5 K。除通道4、5 这两个通道的波动本身就很小外，其余通道偏差的波动得到改善。从2017 年—2019 年3 年期间抽取的代表性60 天验证数据来看，通道3、5、6、7、10、11、12、15 再定标后的观测亮温亮温和模拟亮温最大偏差不超过0.5 K，其余通道最大误差不超过1 K。对于再定标结果仍存在轻微波动的通道，后续会进一步分析非线性系数对再定标模型的影响。

志 谢感谢国家卫星气象中心提供的风云三号湿度计L1 和L0 数据，感谢ECMWF 提供的ERA5每小时再分析数据。