考虑级配影响的珊瑚砂最大动剪切模量试验研究

梁珂 岳冲 周正龙 杭天柱

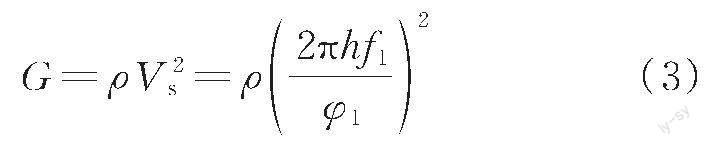
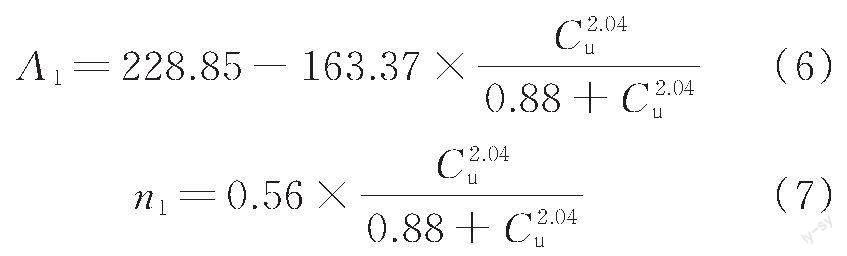
摘要：對不同级配的南沙岛礁珊瑚砂进行共振柱试验，测试不同孔隙比e 的珊瑚砂在20～300kPa 围压下的最大动剪切模量G0，分析不均匀系数Cu、平均粒径d50和细粒含量Fc对珊瑚砂G0的影响，并建立珊瑚砂的G0 经验模型。结果表明：珊瑚砂的孔隙比e 普遍大于陆源砂砾土；同一有效围压σ'0 下，珊瑚砂的G0-e 曲线随Cu的增大而降低，随d50的增大而升高，以Fc≈20% 为界，随Fc的增大先降低后缓慢升高；陆源砂砾土的G0经验模型将低估珊瑚砂的G0值；Fc对G0影响的本质是不同细粒含量的珊瑚砂具有不同的Cu和d50，Cu和d50对G0的影响隐含了Fc对G0的影响。基于Hardin 模型给出考虑Cu、d50 影响的珊瑚砂G0 预测模型，并引入修正系数A'，以考虑颗粒类型等复杂因素的综合影响，采用不同海洋珊瑚砂的试验数据对G0预测模型进行验证。

关键词：珊瑚砂；最大动剪切模量；共振柱试验；级配

中图分类号：TU441；TU411.8     文献标志码：A     文章编号：2096-6717（2023）06-0095-09

Small-strain shear modulus prediction model related to grain gradation of coral sand

LIANG Ke1， YUE Chong1， ZHOU Zhenglong2， HANG Tianzhu2

（1. Key Laboratory of Urban Security and Disaster Engineering of China Ministry of Education， Beijing University of Technology， Beijing 100124， P. R. China； 2.Institute of Geotechnical Engineering， Nanjing Tech University， Nanjing 210009， P. R. China）

Abstract： A series of resonant column tests were conducted on coral sand taken from the Nansha Islands， South China Sea with different grain gradations. The small-strain shear modulus G0 of the coral sands with various void ratio e with the confining stress of 20～300 kPa was obtained. The influence of coefficients of uniformity Cu， mean particle size d50， and fines content Fc on G0 of coral sand was investigated， and the G0 formulation for coral sand was established. For the constant effective confining pressure σ， the curve of G0-e moves downward as the increasing Cu， and moves upward as the increasing d50. The G0 firstly decreases and then increases as the increasing Fc， and the G0 reaches the minimum value for Fc of about 20%. The G0 prediction equations of terrigenous sandy and gravelly soils will obviously underestimate the G0 value of coral sand. The influence of Fc on G0 essentially results from the change of Cu and d50 for coral sand with various Fc. The G0 prediction equation of coral sand related to Cu and d50， which implies the influence of Fc on G0， was proposed， and the correction factor A' related to the morphology and mineralogy of the particle form of coral sands was incorporated in the proposed G0 prediction equation. The validity of the G0 prediction equation was verified by comparing the measured and predicted G0 values of coral sands from different seas.

Keywords： coral sand； small-strain shear modulus； resonant column test； grain gradation

土的动剪切模量G 是场地地震反应分析必需的参数之一，G 随剪应变幅值γa 的增大而衰减。当γa小于10-6时，土体可视为线弹性体，该状态的G 称为小应变（最大）动剪切模量G0。测试G0 的室内试验主要有共振柱试验和弯曲元试验。Yang 等[1]对比了弯曲元和共振柱试验测试的G0，弯曲元测得的G0略大于共振柱试验测得的G0，但两者误差不超过10%；顾晓强等[2]对比了弯曲元、共振柱和循环扭剪试验测得的干砂的G0，发现3 种试验测试的G0 结果具有很好的一致性。现有研究表明，砂土G0受孔隙比e 和有效围压σ'0 的影响较显著。G0随σ'0 的增加呈幂函数增长关系；同一σ'0 下，G0 随e 的增大而减小。Hardin 模型[3-4]是经典的砂土G0预测模型。

另一类常用的砂土G0预测模型修正了Hardin模型中的孔隙比项函数表达式。

式中：A、b、c、n为与材料有关的试验参数；Pa为大气压，100 kPa。

研究表明，级配曲线、颗粒形状、矿物成分等也是砂土G0 的重要影响因素。级配特征可以通过不均匀系数Cu、平均粒径d50 和细粒含量Fc （粒径小于0. 075 mm 颗粒的质量百分比）等参数来表征。Menq[5]通过共振柱试验发现，相同e 和σ'0 条件下，砂土的G0 随d50 的增加稍有增大，随Cu 的增加而减小。Wichtmann 等[6]试验发现，相同e 和σ'0 条件下，石英砂的G0 随Cu 的增大显著减小，而d50 对G0 的影响不明显。Yang 等[1]试验发现，G0 随d50 的增加略有减小。Liu 等[7]定义复合粒径差Γcom 为砂-细粒混合物中纯砂（clean sand）平均粒径与混合物平均粒径之差，建立了砂-细粒混合物G0 与相应的纯砂G0 的比值与Γcom 的经验模型。毕昇等[8]采用共振柱试验研究了Fc 对南通某海域滩涂砂土动剪切模量特性的影响，发现σ'0 和e 相同时，以Fc≈10% 为界，南通滩涂砂的G0 随Fc 的增大呈先减小后增大的趋势。Payan 等[9]评估了4 个陆源砂的G0 模型，发现已有模型的普适性较差，其原因是未考虑颗粒形状的影响，并给出了考虑颗粒形状影响的G0 预测模型。Senetakis 等[10]通过对比相同级配下石英砂和火山岩砂的G0试验结果，推断土体的矿物成分对G0也有一定影响。

珊瑚砂是珊瑚死亡后经过长期地质作用形成的特殊岩土介质，颗粒棱角度高、形状不规则、多孔隙、易破碎、易胶结。梁珂等[11]对南沙岛礁珊瑚砂进行了应变控制分级循环三轴试验，发现γa<1×10-4时珊瑚砂动剪切模量衰退特性与陆源砂砾土的差异显著。Ha Giang 等[12] 采用弯曲元测试了Abu Dhabi 珊瑚砂的G0，发现珊瑚砂的G0比石英砂的大；σ'0 和e 相同时， 珊瑚砂的G0 随Cu 的增大而减小。Morsy 等[13]对埃及的珊瑚砂进行了共振柱试验研究，发现珊瑚砂G0- σ'0 关系的幂指数n 比石英砂的大。

现有研究大多忽略了d50对G0的影响，Fc的影响研究通常独立于其他级配参数，且鲜有关于珊瑚砂G0特性的系统性研究。笔者针对中国南沙岛礁珊瑚砂进行了一系列共振柱试验，系统研究Cu、d50和Fc对珊瑚砂G0的影响， 并建立珊瑚砂G0经验模型。

1 试验材料与试验过程

1.1 试验珊瑚砂

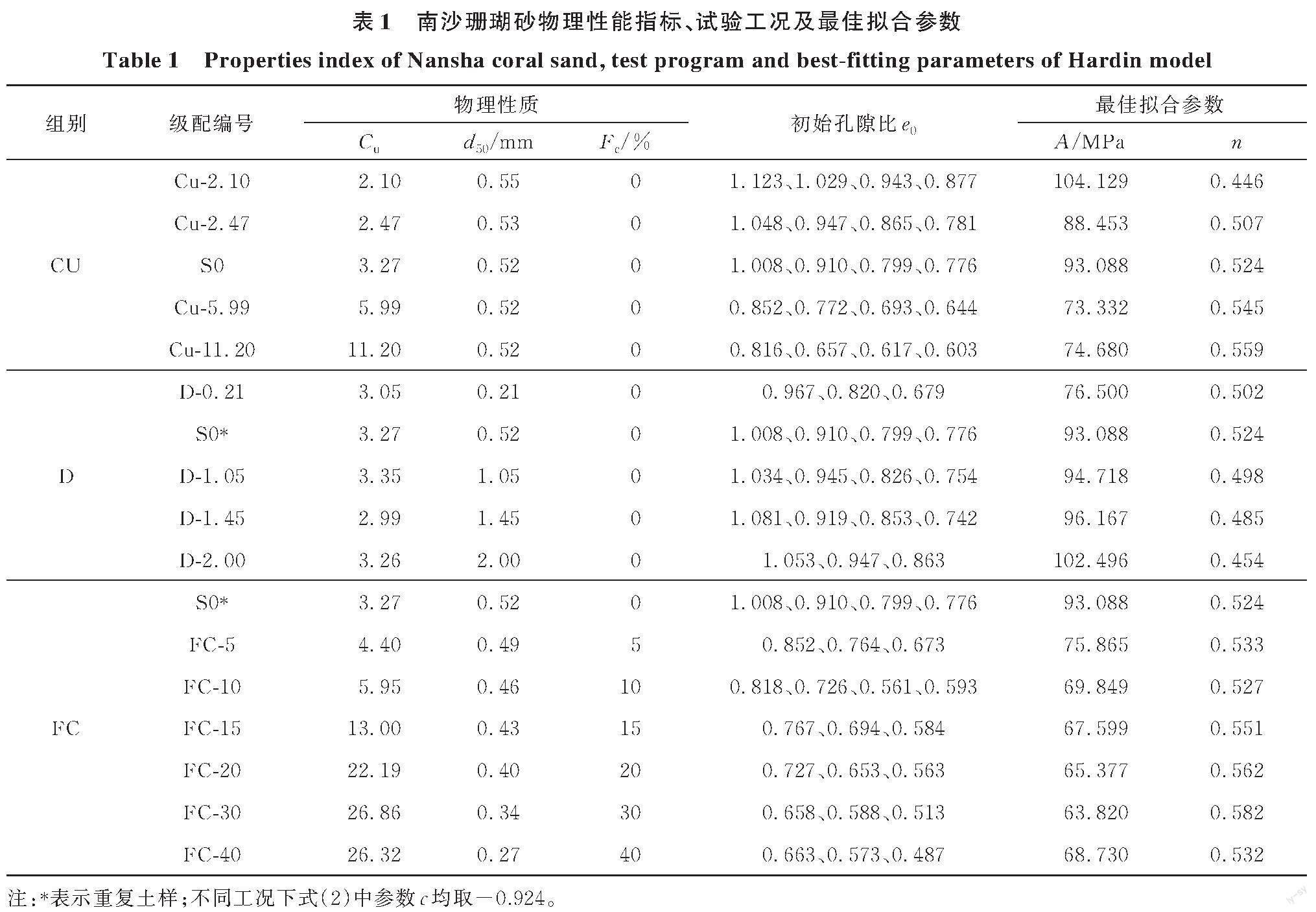
珊瑚砂取自南沙群岛某岛礁，颜色为白色，颗粒比重Gs=2.77。物相分析结果表明，南沙岛礁珊瑚砂的主要矿物成分为文石、高镁方解石和方解石，它们的质量百分比分别为55.5%、41.5%和3.0%。如图1所示，珊瑚砂颗粒形状不规则，棱角度高。为研究级配对珊瑚砂G0的影响，设计了15组级配（图2），按研究目的分成3组。CU组：珊瑚砂级配仅Cu不同（Cu=2.10～11.20），其他参数一致或接近（d50≈0.53 mm，Fc=0%），主要研究Cu对珊瑚砂G0的影响；D组：仅d50不同（d50=0.21～2.00 mm），Cu接近（Cu≈2.95），Fc一致（Fc=0%），主要研究d50对珊瑚砂G0的影响；FC组：主要为不同细粒含量的珊瑚砂-粉混合土，在级配编号为S0的纯砂中分别掺入Fc=0%～40%的细粒，以研究Fc对珊瑚砂G0的影响，并用于验证珊瑚砂G0模型。南沙珊瑚砂的具体物理性质见表1。由表1可知，随着Fc的增大，Cu先增大后缓慢减小，当Fc≈30%时，Cu最大；d50随Fc的增大而减小。

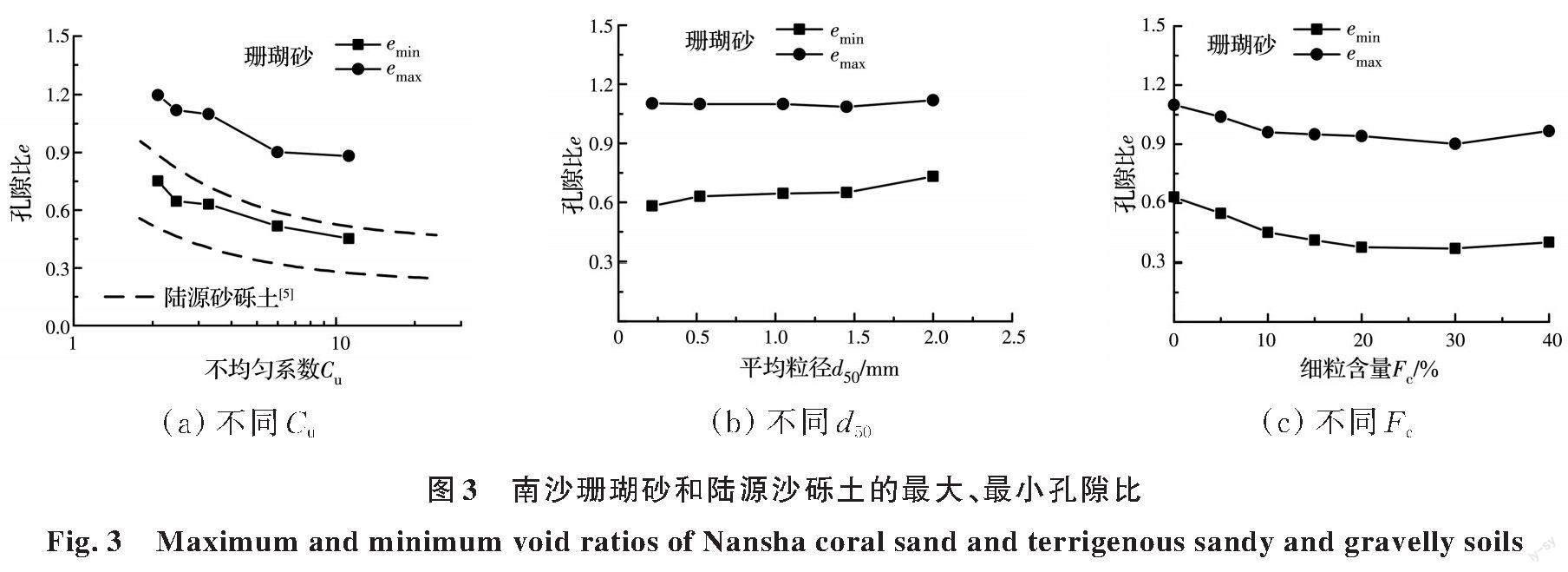
如图3所示，南沙珊瑚砂的最大孔隙比emax和最小孔隙比emin均随Cu的增大而减小；emax随d50变化不明显，emin随d50的增大而缓慢增大；以Fc=30%为界，emax和emin随Fc的增大先减小后增大。Menq[5]总结了陆源砂砾土的emax、emin平均曲线（图3（a）），珊瑚砂的孔隙比远大于陆源砂砾土，主要原因是：1）珊瑚砂颗粒形状不规则且棱角度高，导致珊瑚砂的孔隙比更大[14]；2）珊瑚砂含有大量内孔隙，部分内孔隙与外界连通，成为颗粒的表面孔隙，导致珊瑚砂的孔隙比比陆源砂砾土的大。

1.2 试验过程

试验采用美国GCTS公司研制的TSH-100“固定-自由”型共振柱仪，如图4所示，仪器性能指标详见文献[15]。固结压力通过气压伺服系统控制，试样底部固定，顶部采用全自动悬浮扭转马达进行激振，土样剪应变由顶部马达延长臂上加速度传感器测得。保持激振荷载不变，通过扫频激振方式确定试样剪应变幅值最大时的共振频率f1，动剪切模量G通过式（3）确定。

式中φ1根据式（4）计算。

φ1 tan （ φ1 ）= Iθ /It （4）

式中：ρ为试样密度；Vs为剪切波速；h为试样高度；Iθ为圆柱试样绕轴线的转动惯量；It为顶部所有参振部件的转动惯量。

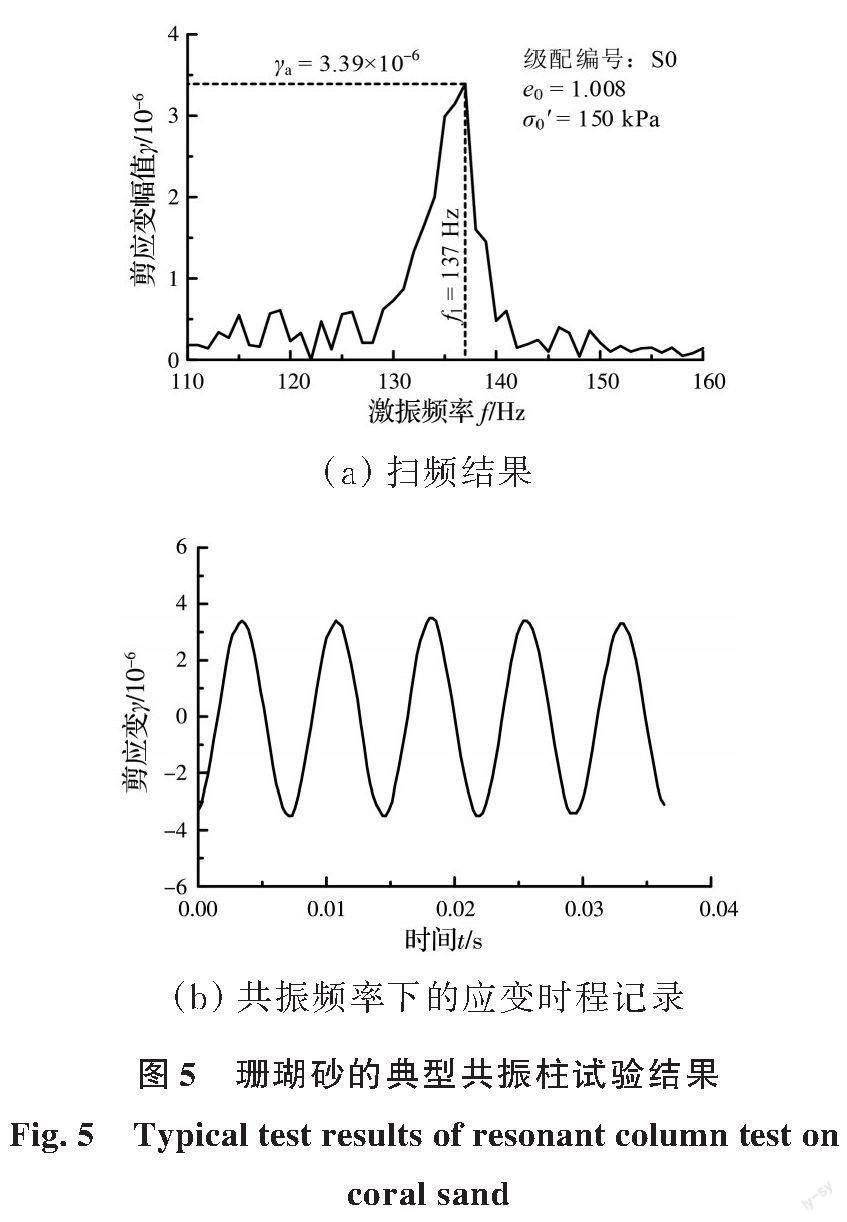
图5为典型的共振柱扫频激振试验结果，不同激振频率下试样的应变幅值如图5（a）所示，由此获得相应激振剪应变γa最大時的共振频率。共振频率下试样的应变时程如图5（b）所示。

试样直径50 mm、高度100 mm，制样方法参考文献[11]。每组级配按不同初始孔隙比e0配制3～4个试样（表1），联合采用通CO2、通循环无气水与施加反压（200 kPa）3种方法进行饱和，使B值大于0.95。

由于试验为无损测试，可对同一试样按σ'0=20、50、100、150、200、300 kPa 的次序进行等压固结和共振柱试验，每级固结时间不少于30 min，并记录试样的体应变εv，由此计算每级固结后试样的实际孔隙比e。每级固结完成后，均对试样进行激振，测试小应变幅值γa （10-6量级）下的G 即为最大动剪切模量G0。

2 试验结果及G0预测模型

2.1 试验结果

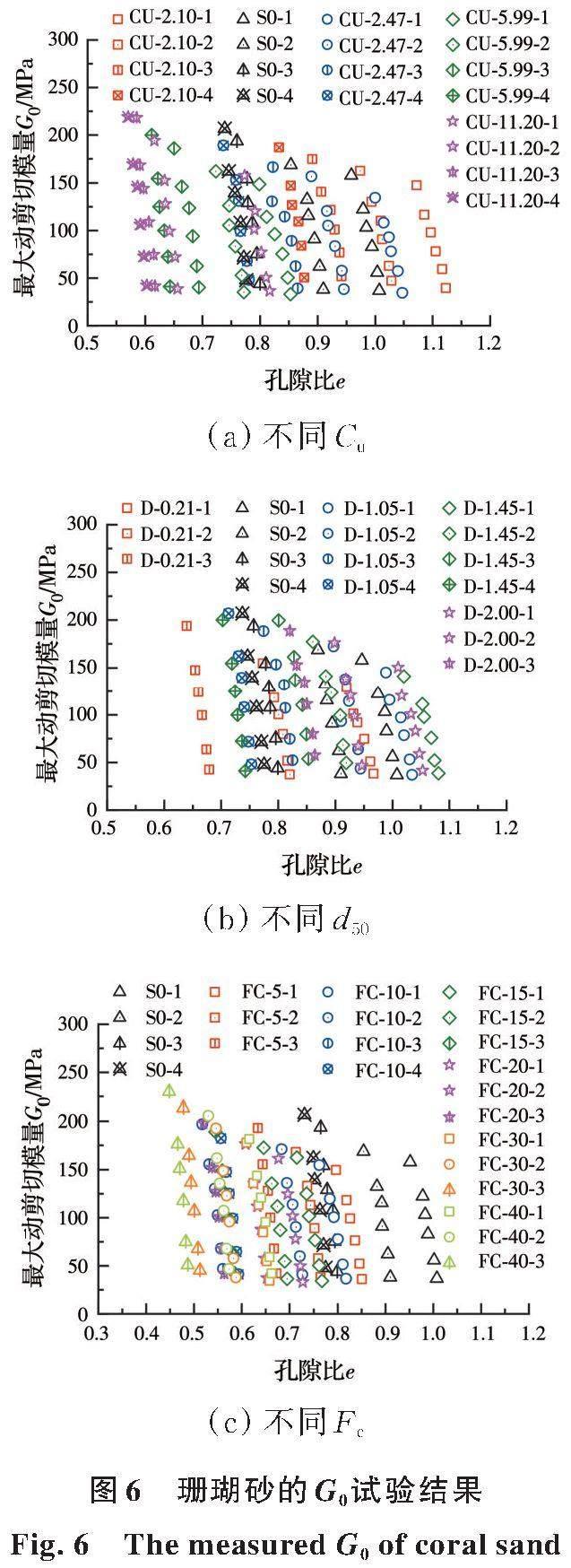
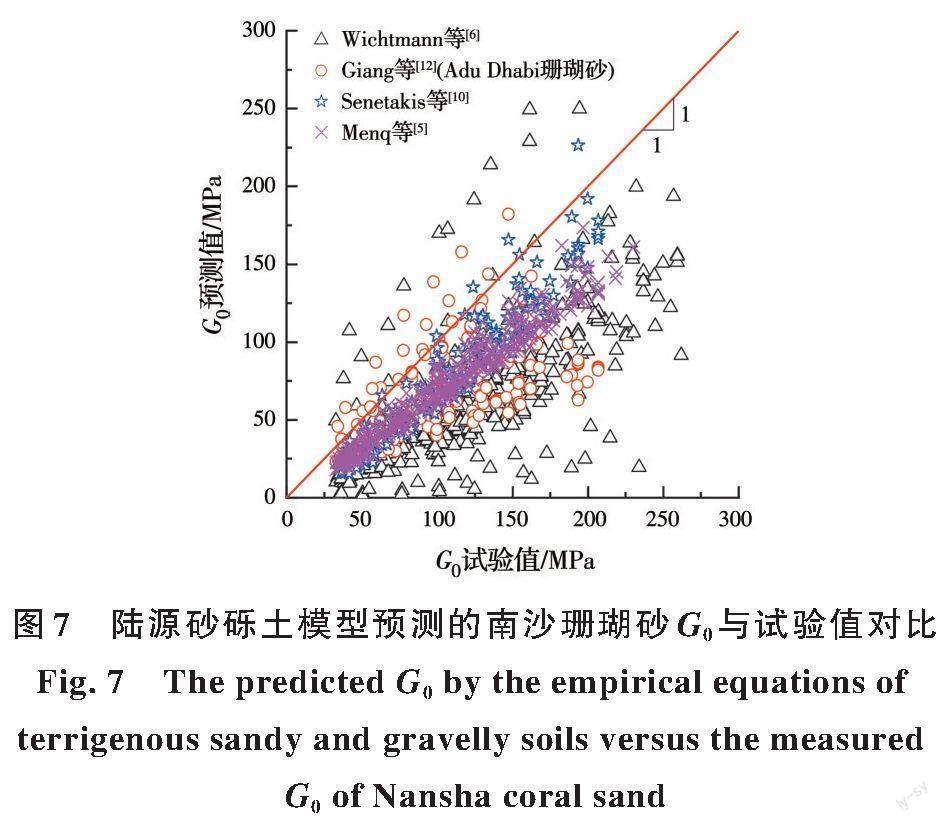
所有53个南沙岛礁珊瑚砂试样的G0测试结果如图6所示，图例中试样编号的末位数字为同一级配下e0从大到小次序的序号。表2总结了部分典型的G0经验模型[5-6，10，12]。采用现有G0模型对南沙珊瑚砂G0值进行预测，如图7所示。可以发现：式（2）形式的G0模型，尤其是Menq[5]模型和Senetakis等[10]模型预测结果的离散性较小；陆源砂砾土的G0模型低估了约40%的南沙珊瑚砂G0值。

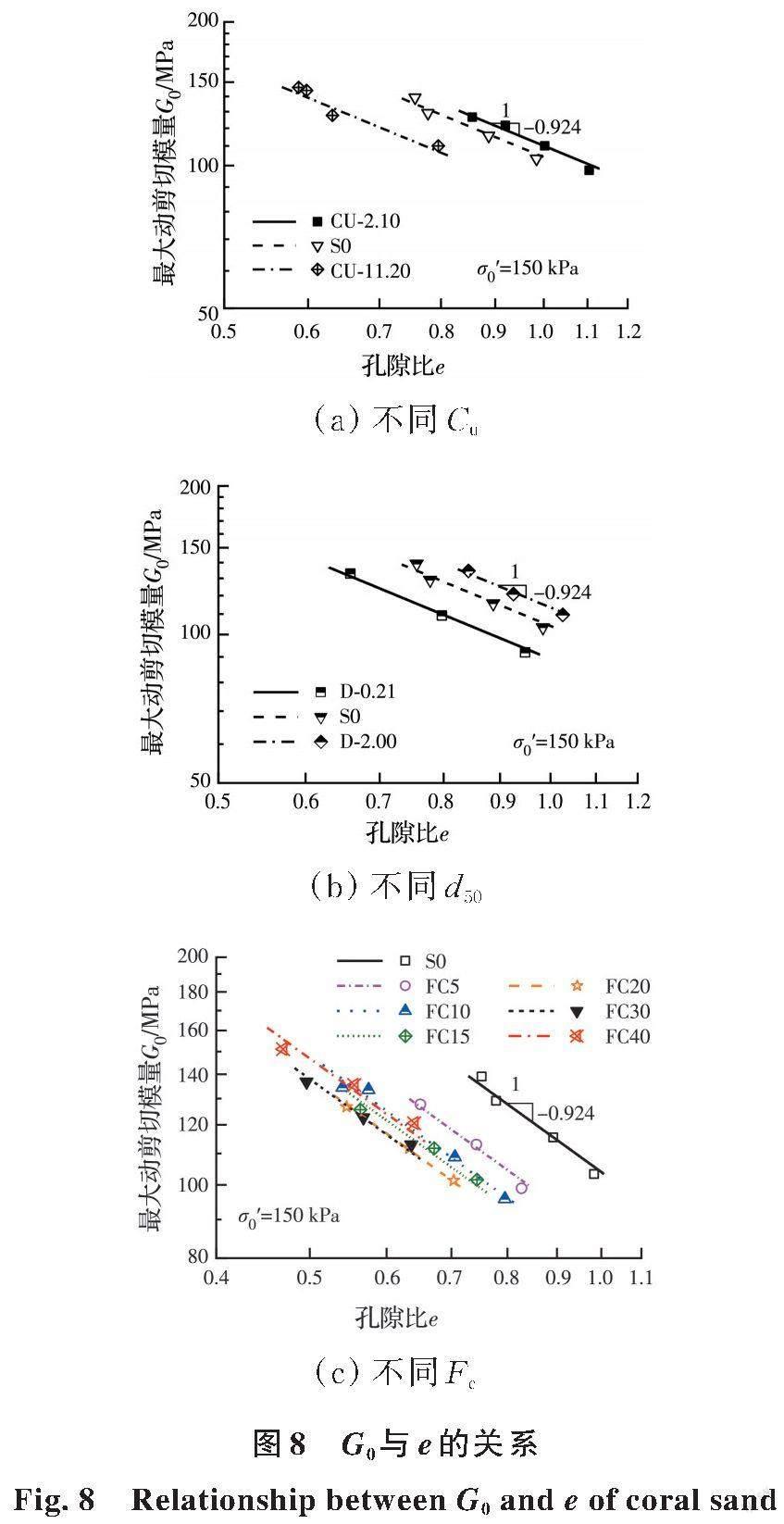
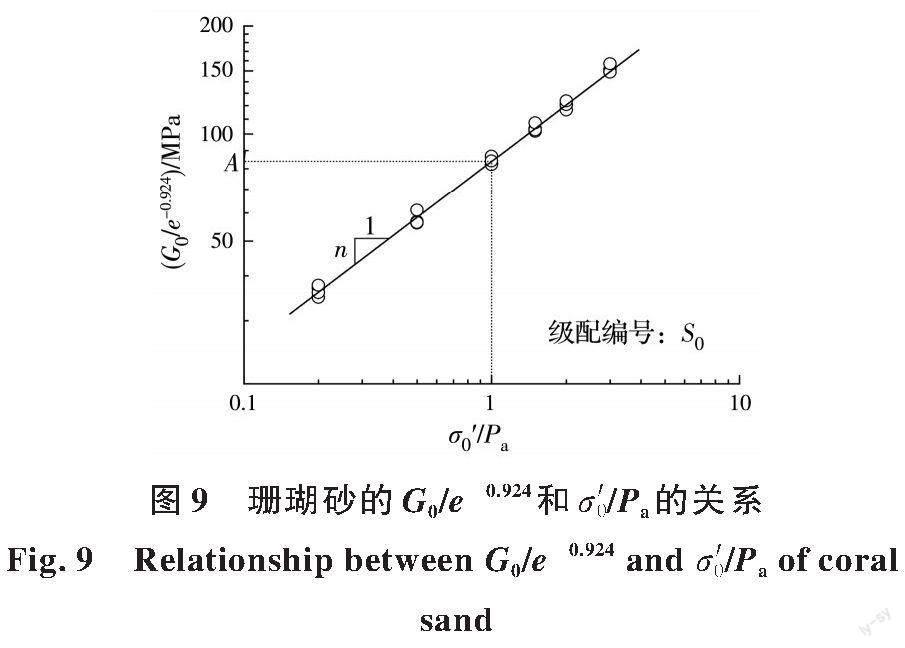
基于式（2）的形式建立珊瑚砂的G0 预测模型。图8 为相同σ'0（150 kPa）下珊瑚砂G0 与e 的关系，可以发现：1）双对数坐标中，同一σ'0 下的G0-e 呈直线关系，其斜率即为式（2）中的参数c；2）不同级配的lg G0-lg e 曲线互相平行，说明参数c 的取值（-0. 924）与级配无关，与Payan 等[9]的结论一致；3）同一σ'0 下，珊瑚砂的G0-e 曲线随Cu 的增大而降低（图8（a）），随d50 的增大而上移（图8（b）），以Fc≈20% 为界，随Fc 的增大先降低后稍微上移（图8（c））。将G0按G0/e-0. 924进行规准化，如图9 所示，在双对数坐标中，G0/e-0. 924-σ'0/Pa 同样呈直线关系，其斜率即为式（2）中的参数n，σ'0/Pa=1. 0 时对应的G0/e-0. 924 值即为式（2）中的参数A。不同工況下，采用式（2）拟合的参数A 和n 的最佳拟合结果见表1。

2.2 G0预测模型

通常假设Cu、d50和Fc对砂砾土G0的影响相互独立[9]，则式（2）可改写为

G0 = A1 （Cu ） A2 （d50 ） A3 （ Fc ） e-0.924 ⋅

（σ0'/Pa ） n1 （Cu ） n2 （d50 ） n3 （ Fc ） （5）

式中：A1、n1是与Cu有关的函数；A2、n2是与d50有关的函数；A3、n3是与Fc有关的函数。

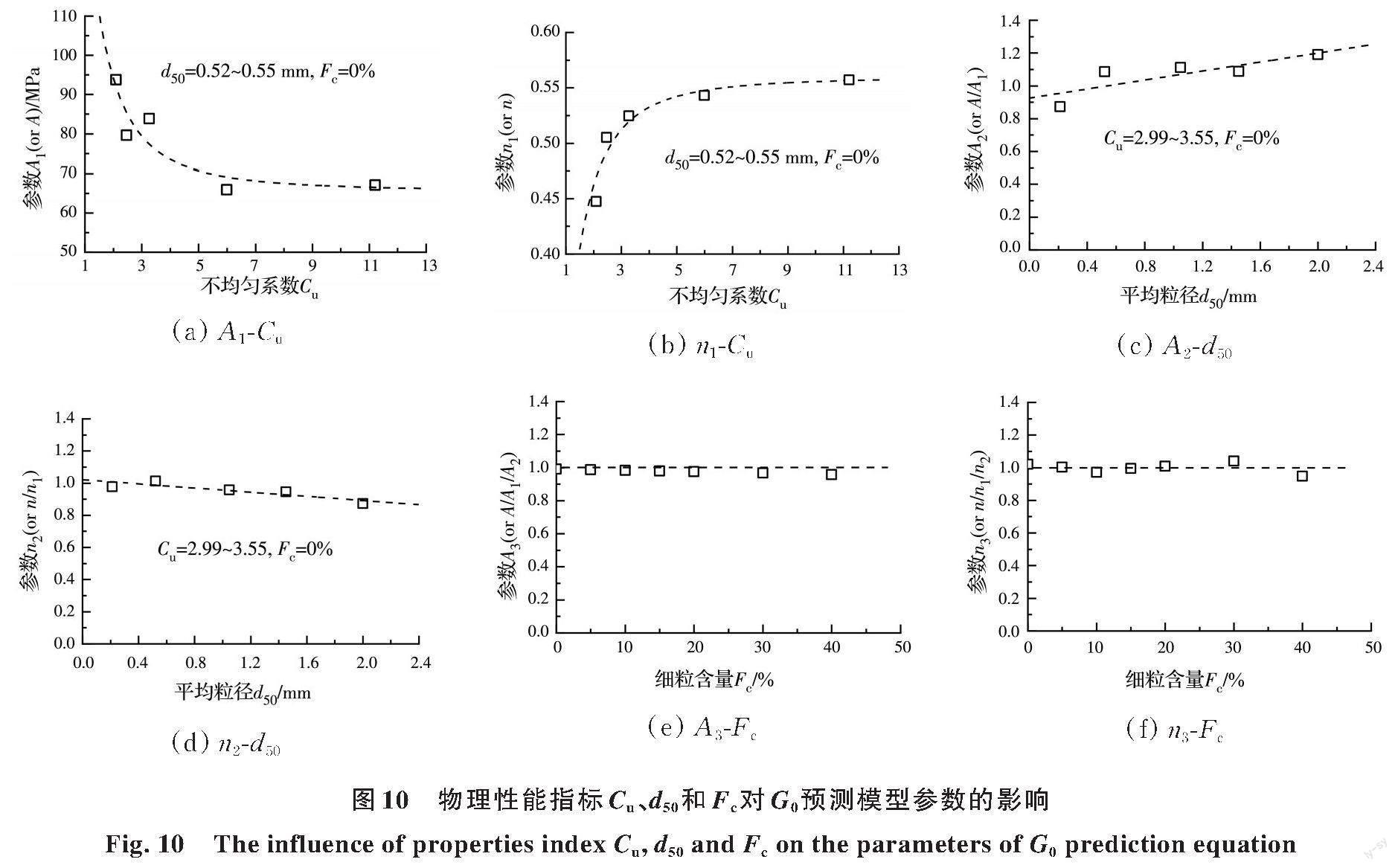
CU组试样的d50几近相同，Fc=0%，参数A和n的变化主要由Cu的变化引起，参数A随Cu的增大而减小，且减小的速率逐渐减慢（图10（a））；参数n随Cu的增大而增大，且增大速率逐渐减慢（图10（b））。参数A1和n1的最佳拟合表达式为

D组试样的Cu几近相同，Fc=0%，将D组试验结果拟合的A和n分别对A1和n1规准化，得到消除Cu影响的A2（A/A1）和n2（n/n1）。A2随d50的增大而线性增大（图10（c）），n2随d50的增大而线性减小（图10（d）），由此，参数A2、n2可表示为

A2 = 0.92 + 0.137d50 （8）

n2 = 1.02 - 0.065d50 （9）

FC组土样的Cu和d50均随Fc变化（表1）。同样，FC组试验结果拟合的A和n分别对A1×A2和n1×n2规准化，消除Cu和d50的影响，得到A3（A/A1/A2）和n3（n/n1/n2）随Fc的变化关系。A3随Fc的增大而略有减小（图10（e）），n3随Fc无明显变化规律（图10（f））。Fc从0%增加至40%，A3和n3的变化均不超过5%。因此，相比于Cu和d50对珊瑚砂G0的影响，Fc的影响可以忽略。Fc对珊瑚砂G0影响的根本原因是：Fc变化引起Cu和d50的改变，从而导致珊瑚砂的G0发生变化，也即，Cu和d50对G0的影响隐含了Fc对G0的影响。

现有研究表明：砂类土的G0和σ'0 的关系与颗粒类型（颗粒形状、矿物特性）有很强的相关性[10，12，16]。引入修正系数A'，以考虑颗粒类型等未涉及因素对珊瑚砂G0的综合影响，则珊瑚砂G0经验模型可采用式（10）表示。

G0= A'A1 （Cu ） A2 （d50 ） e-0.924 （σ0'/Pa ） n1 （Cu ） n2 （d50 ） （ 10）

3 G0预测模型验证

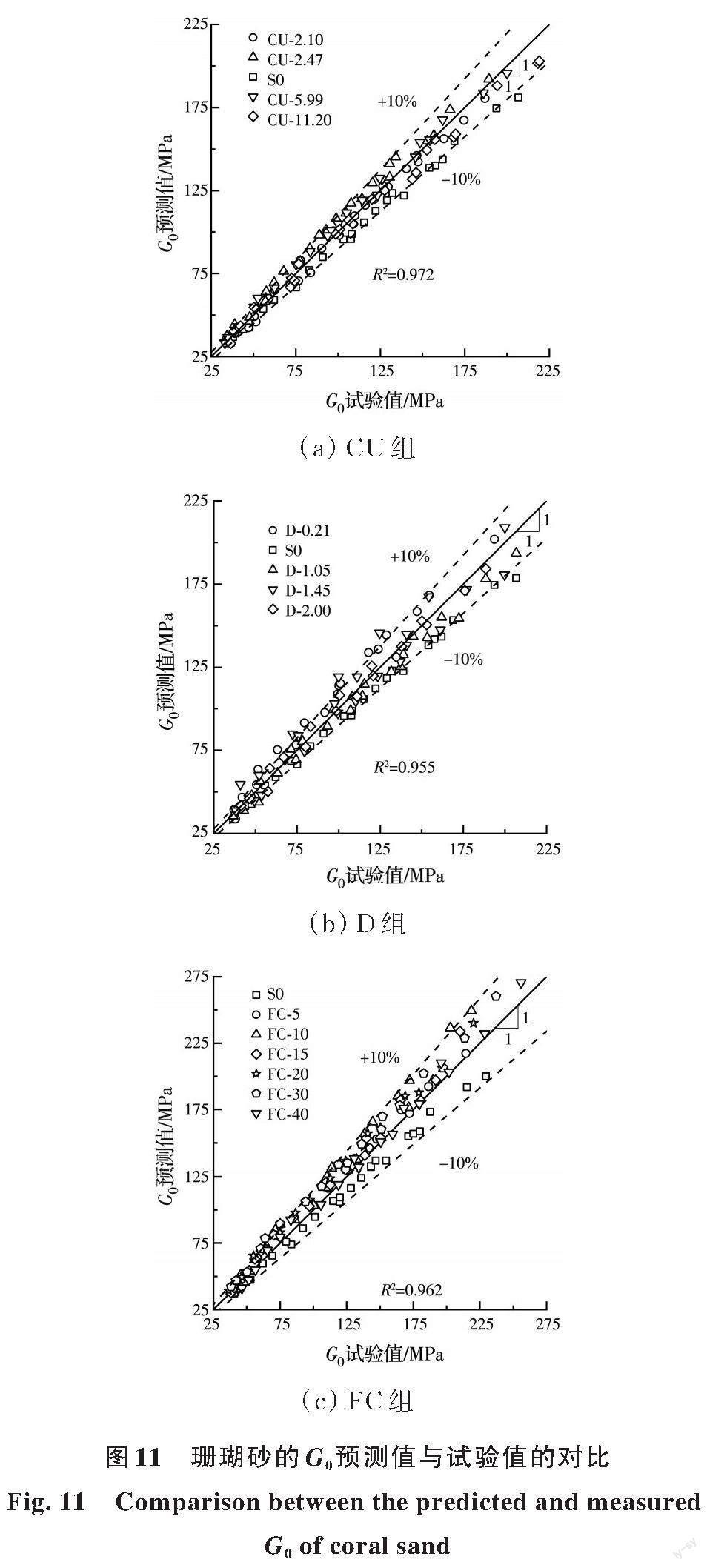
图11（a）、（b）对比了基于CU组和D组试验结果建立的G0预测模型的预测值和试验值。由图可见，预测值的相对误差基本都不超过10%，且散点均匀地分布在45°线两侧。

在G0预测模型式（10）中，Fc的影响是隐式的，FC组的G0预测值和试验值的对比结果如图11（c）所示，相对误差不超过10%，说明Fc对珊瑚砂G0的影响确实已隐含在Cu和d50对G0的影响中。

为验证G0预测模型式（10）对不同海洋珊瑚砂的适用性，对西沙岛礁珊瑚砂试样也进行了共振柱试验，并获取了文献中其他3个海洋珊瑚砂的G0试验值[12-13，17-18]，相应的物理性质指标见表3。不同海洋珊瑚砂的emax和emin具有显著差异，主要原因是不同海洋珊瑚砂的颗粒形状差异较大，且其矿物成分不完全相同，如南沙珊瑚砂主要为珊瑚碎屑，颗粒多为粒状和杆状；而西沙珊瑚砂含有较多的贝壳碎屑，多片状颗粒，颗粒的不规则性强于南沙珊瑚砂。如图12（a）所示，当不考虑珊瑚砂颗粒类型影响时（A'统一取1.0），对不同海洋的珊瑚砂，G0预测模型式式（10）预测值与试验值的散点不再均匀地分布在45°线两侧，在比例上存在一定差异，需向两侧旋转偏移一定角度，但同类珊瑚砂的G0预测值与试验值散点的离散程度比较小，说明式（10）可靠地揭示了级配特征对珊瑚砂G0的影响，只需对G0预测模型式（10）进行简单修正，即可适用于不同海洋珊瑚砂的G0预测。

根据图12（a），颗粒类型修正系数A'的取值列于表3。由图3可知，极限孔隙比emax和emin与颗粒级配、颗粒形状等特征具有显著相关性。Yilmaz等[19]、Chen等[20]采用极限孔隙比作为综合表征土体物理特征内在物理量，并用于评估饱和砂砾土的液化敏感性。笔者参考上述研究，同样采用极限孔隙比综合反映土体级配、形状、矿物类别等因素，评估G0模型的系数A'，并进一步发现A'随珊瑚砂emax和emin的增大而增大，可采用式（11）估算。

根据式（11）估算A'，式（10）计算的不同海洋珊瑚砂G0预测值与试验值的对比如图12（b）所示，除个别数据点外，G0预测模型式（10）对不同类型珊瑚砂G0的预测误差小于20%，且散点也均匀地分布在45°线两侧。对于G0的预测，这样的误差在工程实践中是可以接受的。这表明G0预测模型式（10）具有较好的普适性。

4 结论

通过15 组不同级配的南沙珊瑚砂的共振柱试验，研究了孔隙比e、平均有效围压σ'0、不均匀系数Cu、平均粒径d50 和细粒含量Fc 对最大動剪切模量G0的影响，主要结论如下：

1）陆源砂砾土的G0 经验模型低估了约40% 的珊瑚砂G0值。

2）同一σ'0 下，珊瑚砂的G0-e 曲线随Cu 的增大而降低，随d50 的增大而升高，以Fc≈20% 为界，随Fc的增大先减小后稍微增大。

3）Fc对G0影响的本质是不同Fc的珊瑚砂具有不同的Cu和d50，Cu和d50对G0的影响隐含Fc对珊瑚砂G0的影响。基于Hardin模型，提出了与Cu、d50相关的珊瑚砂G0预测模型。

4）引入与emax和emin有关的修正系数A'，以考虑G0预测模型建模过程中未涉及的颗粒类型等复杂因素的综合影响。采用南沙、西沙及文献中其他3类的珊瑚砂对模型进行验证，结果表明，G0预测模型适用于不同海洋的各类珊瑚砂。

参考文献

[1]  YANG J， GU X Q. Shear stiffness of granular material at small strains： Does it depend on grain size [J]. Géotechnique， 2013， 63（2）： 165-179.

[2]  顾晓强， 杨峻， 黄茂松， 等. 砂土剪切模量测定的弯曲元、共振柱和循环扭剪试验[J]. 岩土工程学报， 2016， 38（4）： 740-746.

GU X Q， YANG J， HUANG M S， et al. Combining bender element， resonant column and cyclic torsional shear tests to determine small strain shear modulus of sand [J]. Chinese Journal of Geotechnical Engineering， 2016， 38（4）： 740-746. （in Chinese）

[3]  HARDIN B O， DRNEVICH V P. Shear modulus and damping in soils： Design equations and curves [J]. Journal of the Soil Mechanics and Foundations Division， 1972， 98（7）： 667-692.

[4]  HARDIN B O， RICHART F E Jr. Elastic wave velocities in granular soils [J]. Journal of the Soil Mechanics and Foundations Division， 1963， 89（1）： 33-65.

[5]  MENQ F. Dynamic properties of sandy and gravelly soils [D]. Austin： The University of Texas， 2003.

[6]  WICHTMANN T， TRIANTAFYLLIDIS T. Influence of the grain-size distribution curve of quartz sand on the small strain shear modulus Gmax [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2009， 135（10）： 1404-1418.

[7]  LIU X， YANG J. Influence of size disparity on small-strain shear modulus of sand-fines mixtures [J]. Soil Dynamics and Earthquake Engineering， 2018， 115： 217-224.

[8]  毕昇， 陈国兴， 周正龙， 等. 细粒含量及固结应力对饱和砂土动剪切模量和阻尼比影响试验研究[J]. 岩土工程学报， 2017， 39（Sup1）： 48-52.

BI S， CHEN G X， ZHOU Z L， et al. Experimental study on influences of fines content and consolidation stress on shear modulus and damping ratio of saturated sand [J]. Chinese Journal of Geotechnical Engineering， 2017， 39（Sup1）： 48-52. （in Chinese）

[9]  PAYAN M， et al. Effect of particle shape and validity of Gmax models for sand： A critical review and a new expression [J]. Computers and Geotechnics， 2016， 72： 28-41.

[10]  SENETAKIS K， ANASTASIADIS A， PITILAKIS K. The small-strain shear modulus and damping ratio of quartz and volcanic sands [J]. Geotechnical Testing Journal， 2012， 35（6）： 20120073.

[11]  梁珂， 何楊， 陈国兴. 南沙珊瑚砂的动剪切模量和阻尼比特性试验研究[J]. 岩土力学， 2020， 41（1）： 23-31， 38.

LIANG K， HE Y， CHEN G X. Experimental study of dynamic shear modulus and damping ratio characteristics of coral sand from Nansha Islands [J]. Rock and Soil Mechanics， 2020， 41（1）： 23-31， 38. （in Chinese）

[12]  HA GIANG P H， VAN IMPE P O， VAN IMPE W F， et al. Small-strain shear modulus of calcareous sand and its dependence on particle characteristics and gradation [J]. Soil Dynamics and Earthquake Engineering， 2017， 100： 371-379.

[13]  MORSY A M， SALEM M A， ELMAMLOUK H H. Evaluation of dynamic properties of calcareous sands in Egypt at small and medium shear strain ranges [J]. Soil Dynamics and Earthquake Engineering， 2019， 116： 692-708.

[14]  CHO G C， DODDS J， SANTAMARINA J C. Particle shape effects on packing density， stiffness， and strength： natural and crushed sands [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2006， 132（5）： 591-602.

[15]  CHEN G X， ZHAO D F， CHEN W Y， et al. Excess pore-water pressure generation in cyclic undrained testing [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2019， 145（7）： 04019022.

[16]  SENETAKIS K， ANASTASIADIS A， PITILAKIS K. Normalized shear modulus reduction and damping ratio curves of quartz sand and rhyolitic crushed rock [J]. Soils and Foundations， 2013， 53（6）： 879-893.

[17]  CATANO J， PANDO M A. Static and dynamic properties of a calcareous sand from southwest Puerto Rico [C]//GeoFlorida 2010. February 20-24， 2010， Orlando， Florida， USA. Reston， VA， USA： American Society of Civil Engineers， 2010： 842-851.

[18]  WANG Y. Dynamic properties of fine liquefiable sand and calcareous sand from resonant column testing [D]. Austin： The University of Texas， 2003.

[19]  YILMAZ Y， MOLLAMAHMUTOGLU M. Characterization of liquefaction susceptibility of sands by means of extreme void ratios and/or void ratio range [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2009， 135（12）： 1986-1990.

[20]  CHEN G X， WU Q， SUN T， et al. Cyclic behaviors of saturated sand-gravel mixtures under undrained cyclic triaxial loading [J]. Journal of Earthquake Engineering， 2021， 25（4）： 756-789.