Kalman滤波算法在海洋钻机中控制信号的优化
刘浩,魏立鑫,尤立春
(1.天水电气传动研究所集团有限公司,甘肃 天水 741000;2.大型电气传动系统与装备技术国家重点实验室,甘肃 天水 741000)
海洋钻机控制系统是大型复杂化的集成设备,对电气传动性能要求严格。以海洋钻机直流控制系统为例,系统5 台柴油发电机组并网运行搭载AC 600 V,3 PH,60 Hz 公共直流母线排形成多机传动结构,并利用西门子6RA80 全数字直流调速技术的7 台可控硅直流调速柜(silicon controlled rectifier,SCR)驱动15 台直流电机,为绞车、泥浆泵、锚机等重要设备提供动力[1-3]。整个控制系统以西门子S7-1500 为核心的双PLC 冷备冗余控制方案,通过现场总线将机具设备组成PROFINET 三级网络,实现设备运行参数的双向传递,所有断路器具体电流依靠跳闸复位(tripping,TRIP)模块进行调节,应急发电机的联络开关不低于3 PH/480 V/500 kW 容量。海洋钻机直流电控系统单线示意图如图1所示,主要由Easy-Gen 3 200全数字发电柜、应急发电柜、SCR 柜、锚机切换柜、综合柜、开关柜、监控综合管理系统(view management system,VMS)等部分组成。由于其应用场景的特殊性,控制信号输出受到干扰因素较多,包括环境、元器件、电磁波等各类外部扰动信号,因此,海洋钻机电控系统并联运行时负荷分配有功/无功功率均≤±5%,且频率波动率约为0.5%,电压稳态调整率为±2.5%。同时,在正常钻井中,谐波畸变含量往往超过35%,需要信号滤波控制策略来保证机械设备的位置、速度、钻压等参数的准确性,进而提升钻井作业的效率。
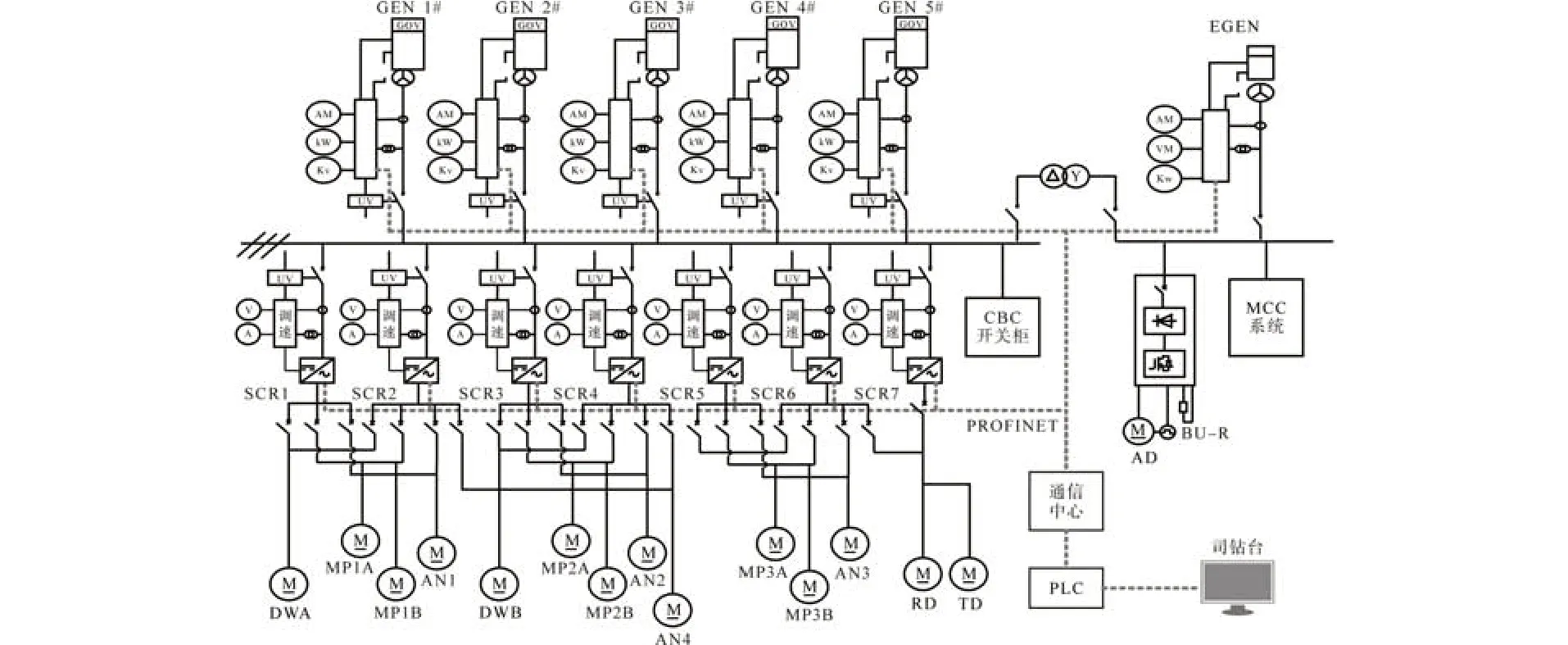
图1 控制系统单线示意图Fig.1 Single line diagram of control system
传统海洋钻机电控系统抑制噪声常用有源电力滤波(active power filter,APF)柜体实现谐波过滤,通过互感器采集负载电流信号,送入以数字滤波器(digital signal processing,DSP)+可编程阵列(field programmable gate array,FPGA)为核心控制的有源滤波控制板,并分解负载电流,计算谐波分量和无功分量,根据计算量的大小反馈补偿信号,实现谐波消除、补偿无功的目的。但是利用APF 进行信号过滤往往带有针对性,而且纯硬件滤波需要复杂的电路控制系统,可靠性、灵活性不能得到完全保证,一般采用硬件+软件数字滤波方式。常用的软件数字滤波方法有一阶滤波算法、算术平均滤波算法、中值滤波算法等,相比于Butterworth,Chebyshev,Bessel等算法[4-7]应用在有噪声的周期性信号中滤波效果难以保证,Kalman滤波算法解决线性滤波问题只需要当前周期测量值和一周期预测值进行状态估计,计算量小,不需要很大的存储空间,简单高效,具备对复杂海洋钻机电控系统各类信号滤波的条件。因此,为了解决多样信号的噪声过大的问题,提出一种基于Kalman滤波算法的PID 控制方式模拟海洋钻机信号优化过程。
1 自整定PID数学模型
PID 控制算法是一个闭环控制算法,且适用于线性、动态特性不随时间变化的系统,主要由比例控制单元、积分控制单元和微分控制单元组成[8],图2为PID控制系统原理图。
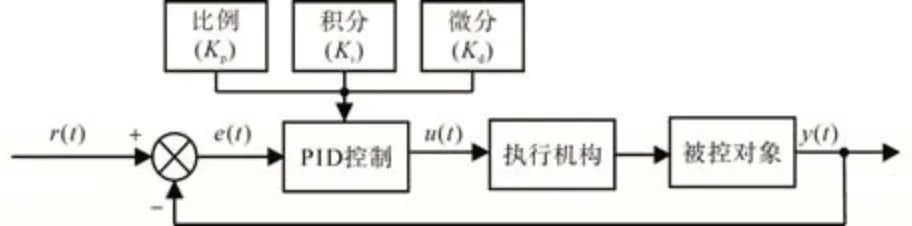
图2 PID控制系统原理图Fig.2 PID control system schematic
简单来说,比例控制单元就是控制当前值,该控制单元仅在系统输出和误差成比例时建立,反映系统当前偏差e(t),系数偏大可加快调节减少误差,但是比例过大会造成系统的不稳定;积分控制单元就是控制过去值,通过之前数据的平均误差来搜索输出结果与设定值平均误差,反映系统累计偏差,调节积分控制单元能消除系统稳态误差,提高无差度;微分控制单元就是控制未来值,反映系统偏差信号变化率,对偏差具有超前预见趋势,可动态调整系统的性能,但是微分控制单元对噪声具有放大作用,因此积分和微分得配合使用,以便控制整体系统的稳定[9]。
根据输入r(t)与输出值y(t)差值构成偏差量e(t),则PID控制公式如下:
其中
e(t)=r(t)-y(t)
式中:e(t)为偏差量;de(t)/dt为系统误差变化率。
根据拉氏域表达式,传递函数如下式所示:
其中
F(s)=f[e(t)]
由于式(1)的时域是通过式(2)拉普拉斯逆变换得到的,因此采用差分方程对式(1)进行离散化处理。
假设采样时间T,在第k时刻可表示偏差为
积分形式采用加和的形式表示为
微分形式用斜率表示为
从而PID的离散数学模型表示为
则PID控制的增量式算法的差分方程表示为
在增量式PID 算法中只对输出做限幅处理,通过对离散化后的比例项、积分项、微分项做参数整定,在一定程度上保证系统控制精度的提升,但是在钻机领域中,PID 的参数整定往往需要人为参与设定调节,和现场调试人员的经验有很大关系,此外人为操作也是造成信号干扰的一种因素。因此,采用临界比例度法整定Kp,Ki,Kd参数值便于后续Kalman滤波算法信号的输入。
临界比例度法首先根据先验知识获取临界度∂k,在闭环控制系统中先将控制器设置为纯比例作用,设置积分时间常数Ti=∞,在干扰的作用下从小到大地逐渐改变控制器的比例度,直到系统产生临界震荡。设临界增益为Ku,临界周期为Tu,则Kp= 0.6Ku,Ki= 0.5Tu,Kd= 0.125Tu,该方法适合在二阶或高阶控制系统。
2 Kalman滤波算法
Kalman滤波算法是一种线性离散维度有限的算法,外部变量的自回归移动可用有理传递函数转换成状态空间表示系统,传统的滤波算法只有在噪声和信号频度不同时才能实现,而Kalman滤波算法在线性状态空间表示的基础上对观测信号和噪声输出进行处理,求取真实信号[10-13]。总的来说,Kalman滤波算法是根据每个变量中所定义的协方差来决定包含的不确定信息,用正态融合模型来预测模型输出和实际测量值,整个过程可以分为预测和观测两部分。预测方程推算当前时刻状态变量和误差协方差估计值,为下一时刻状态构造先验估计,为更新方程结合先验估计和新测量变量改进后验估计[14-17],并且使均方估计误差最小。
离散随机马尔可夫过程状态如下式:
式中:xn为tn时刻的系统状态;fn-1为确定性转移矩阵;un为外部输入;ηn为白噪声;vn为测量误差矢量。
若xn为不可观测状态下的矢量,则其估计值就是试验观测矢量y1:n≡{y1,y2,y3,…}的集合,假设tn时刻的观测矢量与状态矢量之间的关系解析已知,则关系式如下式所示:
式中:yn为观测矢量;hn为确定性观测函数;μn为白噪声,可通过转移函数变化;wn为激励矢量。
根据Chapman-Kolmogorov 方程与式(8)得到状态矢量预测方程如下式:
如果fn-1(xn-1,un)与vn-1不相关,则密度加权预测方差变为如下式所示:
一阶和二阶预测估计是前一时刻观测外的所有观测值,具体而言,假设一阶更新估计值时依赖于当前观测值,即设定线性方程为
式中:A'为未知系数;b为未知截距。
为了使得随机变量xn获得最优线性估计,因此满足每个估计误差值都为0,根据上述要求得到无偏估计如下式:
由于误差估计与观测值满足正交性,如下式所示:
式中:A″为Kalman增益系数,A″=Kn。
因此,最小均方误差(minimum mean square error,MMSE)具体表示如下式所示:
由于Kalman滤波算法适用于任何密度分布的信号形式,因此该算法的预测过程可以先验密度和后验密度直接求解,当系统动态预测过程与观测过程均为线性高斯过程时,Kalman滤波算法是Bayes估计的闭解。
3 Kalman滤波算法的PID控制方式
海洋钻机电控系统大量信号采用基于瞬时无功理论的方法来反映在动态响应时间、超调量等参数上,通常噪声计算速度相对较慢,补偿率低于60%,尤其对于不平衡负载下的零序谐波不能输出滤波指标参数,但Kalman滤波算法能预测当前时刻的状态量,为下一时刻提供先验知识,从而求解下一时刻的状态量,而且对PID 控制来说微分控制的斜率会对偏差进行累加,即使噪声幅度足够小,但是只要达到一定的频率,偏差变化率一样会很大,产生的噪声也就更多,从而对系统造成影响,因此在控制反馈回路中,尽量减少高频噪声进入PID 控制器,因此有必要在微分部分加入Kalman滤波算法以提升信号传输质量,结构如图3所示。

图3 Kalman滤波算法的PID控制Fig.3 PID control of Kalman filtering algorithm
为了验证Kalman 滤波函数在石油钻机电控系统中的滤波有效性,分析传递函数G(x),将正弦信号离散化,通过不断获取系统测量值,递归计算协方差值,从而计算最优估计,整体滤波效果反映于动态响应时间。初始设定干扰信号和测量噪声的协方差因子,定义初始状态空间,采用正弦信号作为标准信号,增加干扰经过滤波获取滤波后的信号以及误差信号。利用Kalman 滤波信号,当增益值越小,表示预测结果越可信,最优值接近于预测值,反之,增益越大,说明最优值越趋近于测量值。
4 实验仿真
实验仿真环境在Windows10 专业版中,仿真硬件设备:CPU 处理器为Intel(R)Core(TM)i7 2.3 GHz;RAM 内存16 G;硬盘内存为1 TB+512GSSD;软件平台为Matlab 2012a/Simulink。
目前,海洋钻机电控系统仍以直流电控和交流电控为主,钻井深度在4 000~9 000 m 范围内,直流控制系统为主流,3 000~12 000 m 范围内,交流控制系统为主流。由于交流变频系统无极调速的优越性能且海洋深井居多,目前市场普遍采用交流变频控制系统逐渐替代直流控制系统。在钻机钻井过程中,PID 参与钻压、速度等重要参数控制,为了更加真实模拟信号数据,外部参数按照电机800 kW 及1 200 kW 制动电阻,钻压按照实际钻压的0.8~1.2倍作为钻压,模拟现场变频器配置框架,如图4所示。
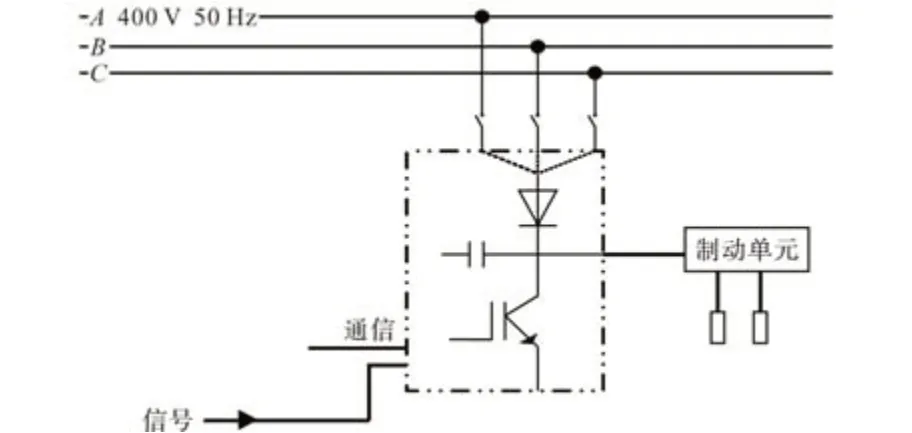
图4 模拟变频器配置Fig.4 Analog converter configuration
首先针对现场电流信号,利用标准正弦波函数替代电流信号,为了更加接近现场数据,在控制干扰信号和测量噪声信号中分别添加幅值均为0.02 的白噪声,输入信号频率约为1.5 Hz 且幅值为1.0,设定控制干扰信号的协方差因子Q为1且测量噪声协方差因子R也为1,仿真时间为5 s,采样周期为1 ms,结果如图5所示。

图5 带有噪声的原始信号Fig.5 Raw signal with noise
从图5 可以看出,随机噪声分布在正弦波形周围,伴随着整个仿真周期,明显该信号不能用于现场控制系统中。经过Kalman滤波器后,得到滤波后的信号波形图如图6所示,从图中可以看出滤波后的信号和理想波形几乎一致,而且根据误差信号协方差变化率可得,整个噪声波形在参与滤波过程中误差很快收敛,证明Kalman滤波算法的有效性。
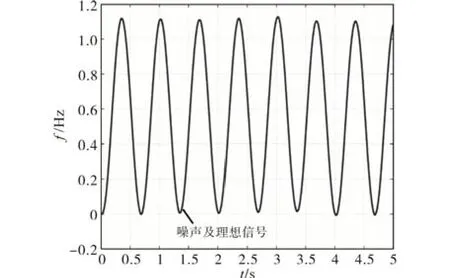
图6 经过Kalman滤波后的信号波形Fig.6 Signal waveform after Kalman filtering
为了进一步观察Kalman滤波算法的性能,设计西门子S120 及CU320 控制单元为核心的变频柜,额定功率1 000 kW、额定电压DC 810 V、频率50 Hz,采取带有Modbus-RTU 通讯协议的温度采集模块,通过8 路薄膜电阻温度传感器获取变频器温度信号,往往现场的温度信号存在一定的伪信号,而且周围温度对实际情况产生的影响较大,利用Kalman 滤波进行温度跟踪,可在一定程度程度上逼近目标值。
图7 为带噪声的温度信号图。根据图7 可知,变频器温度一般稳定在一个固定值,只要温度变化不超过阈值,可以接受当前变频器温度。温度预期值约为24~26 ℃(可调整范围),利用温度传感器采集温度数据添加噪声,可以看出温度变化差距很大,最大温度差距达到接近9 ℃。经过Kalman 滤波后,将信号再平滑处理,消除尖峰信号,结果如图8所示,处理后的信号值明显更加稳定且平滑,信号质量有显著提升。由于PID控制对信号具有很好的控制作用,能使信号快速收敛,采用Kalman滤波算法对PID 控制优化,采样时间为1 s,加入幅值为0.02 的白噪声,输入信号为一阶阶跃输入信号,在PID控制系统仿真中,Kp=8.0,Ki=0.8,Kd=0.2,图9 表示无滤波时的阶跃信号,图10为滤波后的PID阶跃信号。
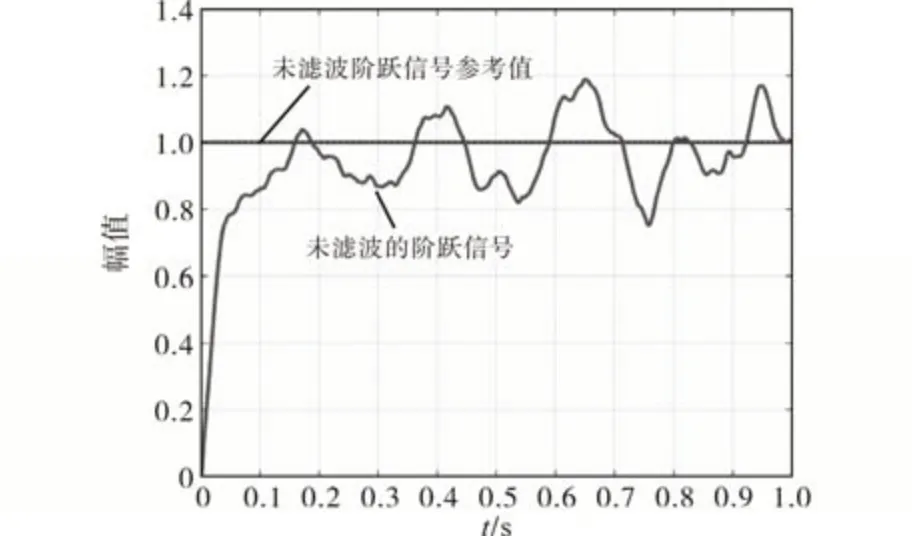
图9 无滤波的PID阶跃信号Fig.9 Non filtered PID step signal
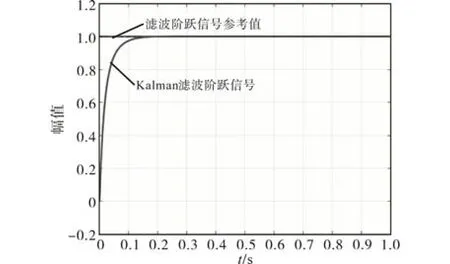
图10 滤波后的PID阶跃信号Fig.10 Filtered PID step signal
从图9、图10 比较可以看出,通过Kalman 滤波后的PID 阶跃响应能很好地收敛稳态,且动态响应时间更短,超调量更小,很好地验证了算法的有效性,后续利用该设计思想,结合实际其他信号做进一步验证。
5 结论
海洋石油钻机PID调节信号传输过程中噪声难以避免,通过对现场常见信号的模拟,利用Kalman滤波算法作为PID 控制信号的滤波过程,去除信号噪声,使得控制方式更加精确且稳定。文章对温度信号、PID 阶跃响应信号做了算法有效性、优越性的验证,在实际工控领域中,可将其应用于石油钻机行业自动化钻机系统中,为设备故障诊断数据分析提供理论依据,验证算法的应用性。因此,该方法在钻机作业领域有着广泛的应用前景。

