基于动力学和声学仿真的损伤伸缩缝跳车噪声特征

孟利波,刘怀林,马东鹏,席尚宾,吴泽康,刘逸平*

(1.重庆物康科技有限公司,重庆 400000; 2.浙江清华柔性电子技术研究院,嘉兴 314000;3.华南理工大学土木与交通学院,广州 516000)

伸缩缝是连接两段公路桥面的装置,在大型车辆通过、温度变化作用下公路桥面会发生变形,而伸缩缝可以调节公路桥面的自由变形,因此伸缩缝在公路桥梁中十分重要。然而,严苛的服役环境和重车作用会使伸缩缝发生损伤,具体体现为接缝处的混凝土破损、钢筋外露、伸缩缝顶起等[1-2]。伸缩缝的病害十分普遍。例如,金丽温高速公路在其通车起的8 a时间内,共有24条伸缩缝发生了不同类型的病害[2];丽泽桥的各桥段病害都与伸缩缝病害密切相关[3]。迄今,国内已发生多起因伸缩缝病害导致的严重事故。2020年11月11日,在广澳高速广州往珠海方向,一辆白色小货车碰撞路面桥梁伸缩缝后失控,造成严重的交通事故。因此,对伸缩缝的健康状态进行实时监测,尽早发现损伤伸缩缝并排除隐患,对保障公路桥梁正常运营至关重要。

中外桥梁伸缩缝的损伤监测主要通过定期人工排查的方法来开展,费时费力同时影响通行。其他监测手段(如安装位移传感器)虽然可以方便地获取与桥梁伸缩缝服役状况相关的数据,但工程上这些采集到的数据不能直接反映伸缩缝的损伤情况,同时诸如挠度、应变等物理量受温度影响较大,往往需要进行被测量与温度的相关性校正[4-6]。因此,这类伸缩缝损伤探测技术与伸缩缝健康监测的工程需求仍存在巨大差距。

声波分析是结构损伤检测的重要方法,其原理是利用声波在有损和无损的材料中传播规律的差异来判定结构物内部是否有损伤。其中,声波CT通过人工激励发射超声信号,在结构物的另一侧接收信号并根据声速构造体图像[7]。但是该技术难以满足高探测精度和长探测距离的要求,克服该缺点的方法是使用超磁致伸缩材料作为发射源,然而该材料价格极其昂贵,不能满足工程上的大规模使用。实际上,由于接缝处的不平整,车辆行驶过模数式伸缩缝时会出现不同程度的跳车现象,跳车荷载产生的噪声本身就是一种良好的激励。充分利用跳车噪声来获取有效信息是桥梁相关科学研究和工程应用的发展趋势。Algohi等[8]在路段两端的伸缩缝处各放置一个麦克风和采集装置以记录车辆通过伸缩缝时的跳车噪声信号,通过数据处理获取特征峰点来计算车辆通过该路段的车速。目前已有学者指出,通过声波分析,跳车噪声信号可以反映出伸缩缝的健康状态;Nishikawa等[9]在汽车上加装噪声采集设备,记录该车通过伸缩缝时的噪声信号,发现通过有损的伸缩缝时声波在200～500 Hz或500～800 Hz有特征频带;Guerreiro等[10]通过对跳车声波信号的傅里叶变换,得到了以金属混响为特征的伸缩缝螺栓松动损伤形式的识别方法,提出了应用程序原型。然而,由于缺乏理论或仿真结果的支撑,将这些研究的成果推广到实际工程使用前仍需经过大量的试验检验其适用性。

利用动力学和声学仿真,可以模拟物体碰撞过程产生的噪声,从而开展噪声特征的研究、方案制定和结构优化等。这种仿真方法已被运用于交通相关领域,例如,李中哲等[11]基于多体动力学的变速器噪声预测方法,准确地预测变速器辐射噪声,为进一步研究变速器噪声优化设计提供参考;李文平等[12]建立了车窗系统的动力学仿真模型和声学仿真模型,实现了轿车车窗上升过程振动响应及噪声仿真;王鹏斌等[13]从噪声对环境舒适性影响的角度,通过动力学和声学仿真研究了轮胎噪声声源。因此,利用动力学和声学仿真模拟车辆车胎与无损/有损伸缩缝的碰撞产生的噪声特征,优化麦克风的布局,技术上可行。

现建立无损和以路面破损导致伸缩缝钢筋外露为典型损伤特征的伸缩缝路段模型,采用动力学仿真获取车胎与伸缩缝碰撞过程的加速度场,并在声学仿真中将其表征为声压,模拟跳车过程中的环境声场,分析声场特征并研究跳车高度对声场的影响,确定用于伸缩缝健康监测的麦克风布局。为基于噪声分析的伸缩缝健康监测提供方案指导。

1 跳车过程动力学-声学仿真

轮胎-伸缩缝的动力学仿真模型如图1所示,其中图1(a)为无损伸缩缝,伸缩缝的C型钢表面与混凝土表面齐平;图1(b)为损伤伸缩缝,混凝土破损后伸缩缝的钢筋部分外露。考虑到计算成本,所有模型几何尺寸按实际尺寸的1/4进行缩放,模型中路面大小为1.5 m×1.5 m×0.25 m,轮胎直径0.35 m,宽度0.08 m,水平速度5 m/s,竖直方向初速度为0,伸缩缝的几何模型参考GQF-C型伸缩缝。对于无损和损伤的伸缩缝,分别选取轮胎和伸缩缝间距0.01、0.03、0.06 m作为跳车高度。考虑到车辆的载重,模型中在轮胎中心点处施加2 450 N、方向竖直向下的集中力。轮胎与伸缩缝间采用罚函数的接触方式设置了接触对,计算不同跳车高度下伸缩缝的动力学响应。动力学计算在商业有限元软件COMSOL中完成。

模型中轮胎为橡胶,伸缩缝为结构钢,路面为混凝土,主要的材料参数如表1所示。其中,由于伸缩缝和路面相较于轮胎刚度较大,在跳车过程中伸缩缝和路面的变形量小,所以在定义本模型中结构钢和混凝土时只需要考虑其线弹性范围的力学属性即可。但是,轮胎在跳车过程中会发生较大变形,因此需要表征橡胶材料的超弹性模型。本文研究采用的是经典的Mooney-Rivlin模型。Mooney-Rivlin模型采用弹性应变能来表征力学性能,考虑到计算成本和计算精度要求,使用Mooney-Rivlin模型2参数形式的本构,表达式为

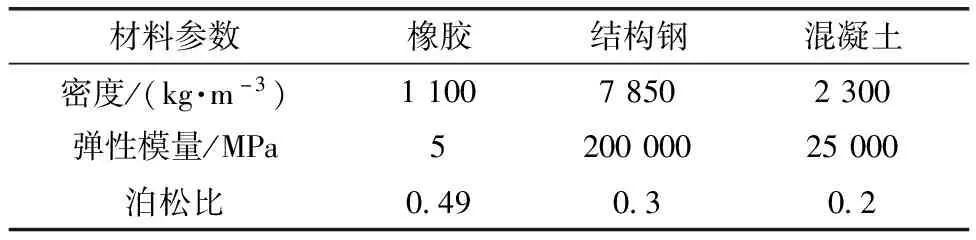
表1 模型材料参数

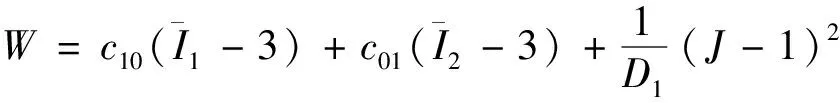
(1)

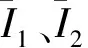
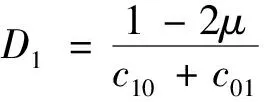
(2)

多体动力学在时域求解,而声学在频域求解。由于声学计算在频域声学范畴下开展,其控制方程采用赫姆霍兹方程,即

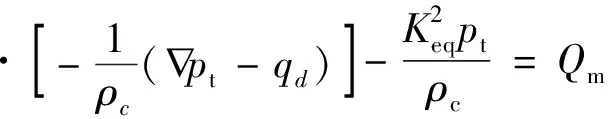
(3)

式(3)中:∇为梯度算子;ρc为材料密度;pt为总声压;qd、Qm分别为单、偶极子源项;Keq为角频率与材料声速的比值。

声学仿真中硬声场边界条件为

(4)

式(4)中:n为表面法向方向。

具体地,在计算中将轮胎与伸缩缝接触区域的法向加速度转换为频域,并用作噪声源,然后执行声学分析,以计算图1(a)中麦克风测点1、2和3的声压级。

2 动力学仿真结果

动力学仿真可以得到跳车过程的应力云图。图2为无损和有损状态下轮胎与损伤伸缩缝接触过程出现最大应力时的应力云图。图3为不同跳车高度下伸缩缝无损和有损状态下的最大应力曲线。可以发现,轮胎与无损伸缩缝接触的最大应力远小于相同跳车高度时损伤伸缩缝的最大应力。无损状态下,最大应力出现在轮胎与伸缩缝接触时的混凝土位置,跳车高度0.06 m时最大应力为2.5 MPa;损伤状态下,最大应力出现在轮胎与伸缩缝接触时的钢筋位置,跳车高度0.06 m时最大应力达到27.1 MPa。

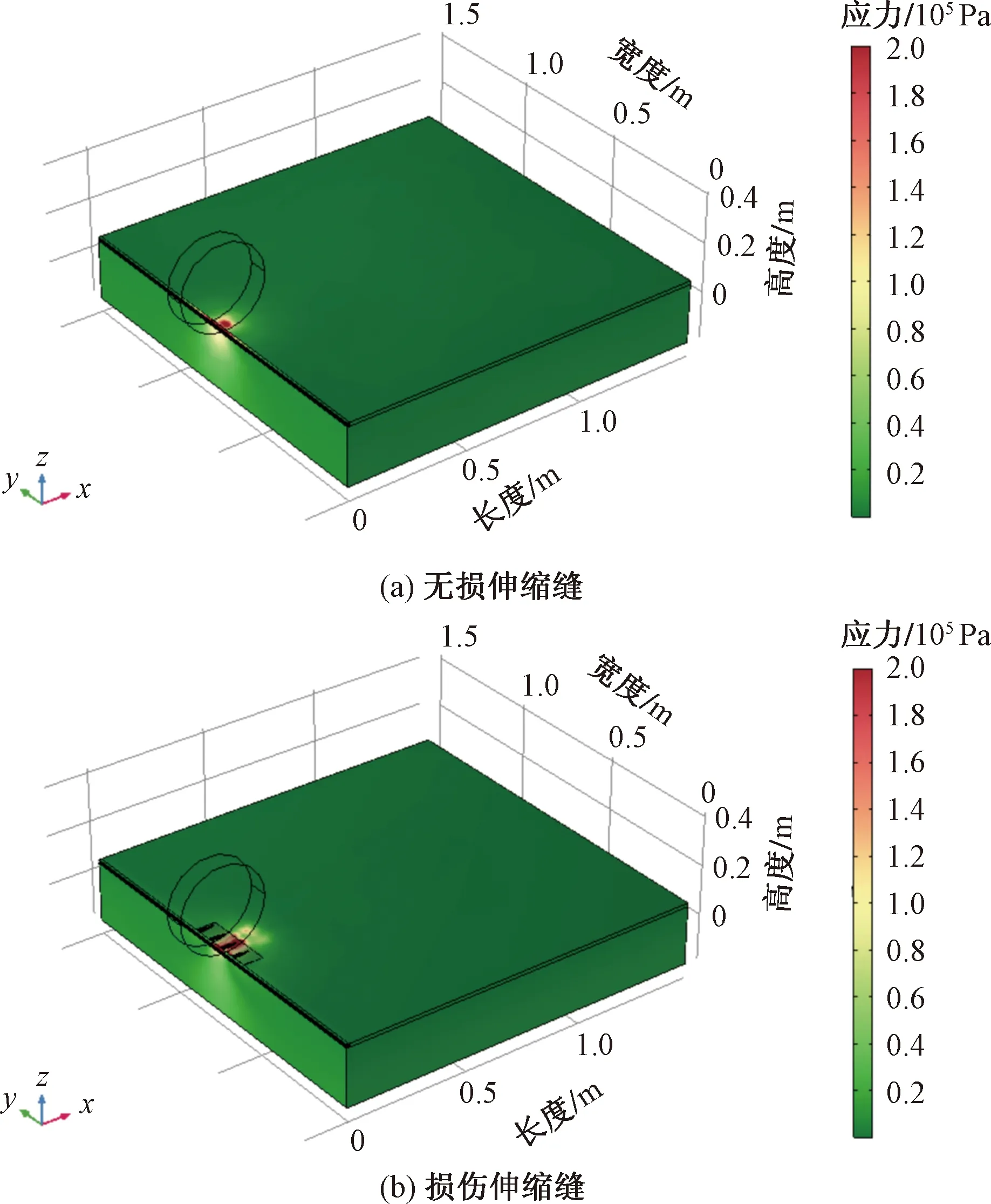
图2 跳车过程伸缩缝应力云图

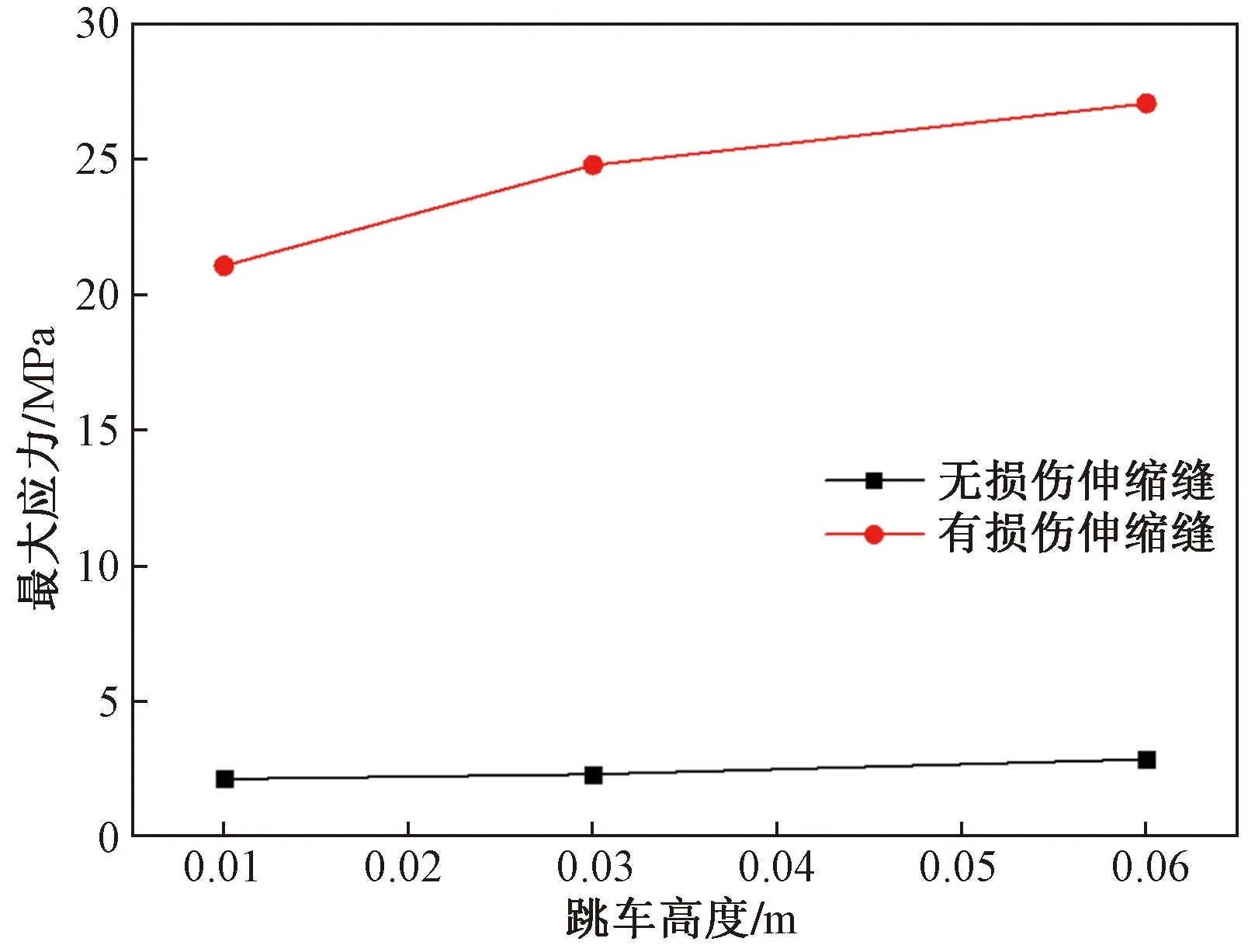
图3 跳车高度-最大应力曲线

图4为不同跳车高度下无损和有损伸缩缝系统的最大加速度曲线。系统的加速度是噪声辐射的量度,在后续的声学仿真中需将其作为声学的声压源,因此对声学仿真十分重要。可以发现,随着跳车高度的增加,系统的最大加速度随之增大,同时在相同跳车高度下有损伸缩缝的最大加速度也显著大于无损的工况。

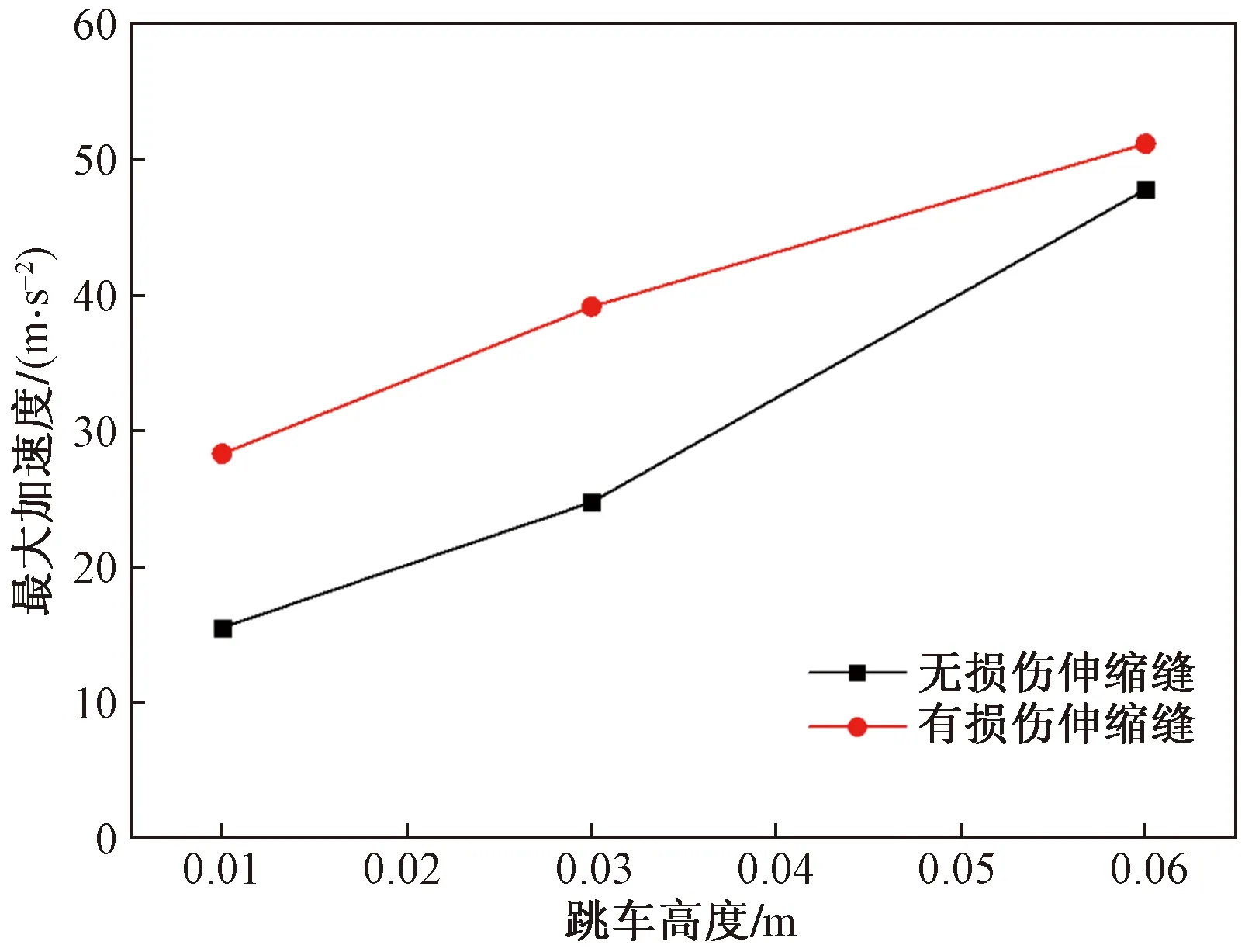
图4 跳车高度-最大加速度曲线

3 声学仿真结果

图5为跳车高度为0.06 m时麦克风测点2处记录到的声压-时间曲线。从图5可以明显看出,相较于损伤伸缩缝下记录到的声波信号,无损状态下的声压幅值更小,同时波形也略微滞后于损伤下的波形。因此,通过麦克风记录到的声压-时间曲线,可以对伸缩缝进行损伤探测。

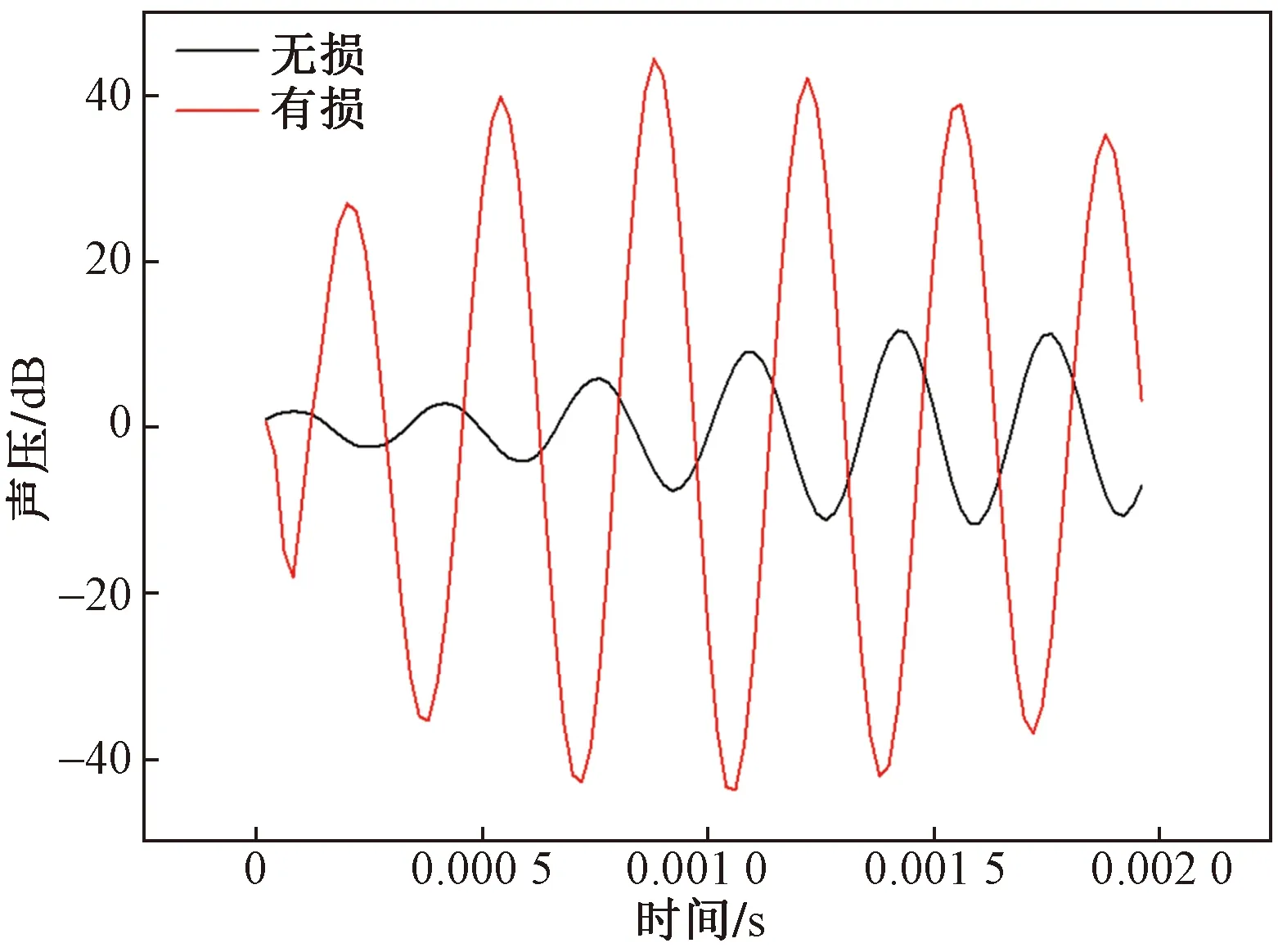
图5 无损和有损伸缩缝下跳车噪声声压-时间曲线

为研究不同麦克风测点的噪声信号差异,以跳车高度0.06 m的损伤伸缩缝为例,调取麦克风1、2和3记录到的声压-时间曲线(图6)。可以发现,随着麦克风远离轮胎与伸缩缝的接触点,声压的幅值会逐渐下降且波形规律基本保持不变,但声压幅值仍明显高于无损状态下的声压幅值。因此,在工程实际中,可以根据实际测量条件在伸缩缝附近布置测点而不影响伸缩缝的健康监测。

图7为声学仿真得到的损伤状态下不同跳车高度的声压级云图。从图7可以发现,对应于图1的麦克风各测点,测点1处的声压大于测点2和3的声压,同时跳车高度对系统声压的影响显著。

图8为麦克风测点1、2和3记录到的声压-时间曲线。从曲线中可以看出,跳车高度对噪声声波频率几乎没有影响,不用跳车高度下声波的波峰和波谷的位置基本保持一致。但是,跳车高度对噪声声压幅值有一定影响。提取图8中的不同跳车产生声波波峰波谷的绝对值,绘制于图9。可以看出跳车噪声的幅值呈现先增后减的趋势,同时跳车高度越大,幅值上升的速度也越大。波峰波谷的最大幅值也呈现跳车高度越大幅值越大的规律,可以看出,跳车高度0.06 m时的最大声压幅值约为0.01 m时的1.3倍,约为0.03 m时的1.1倍。

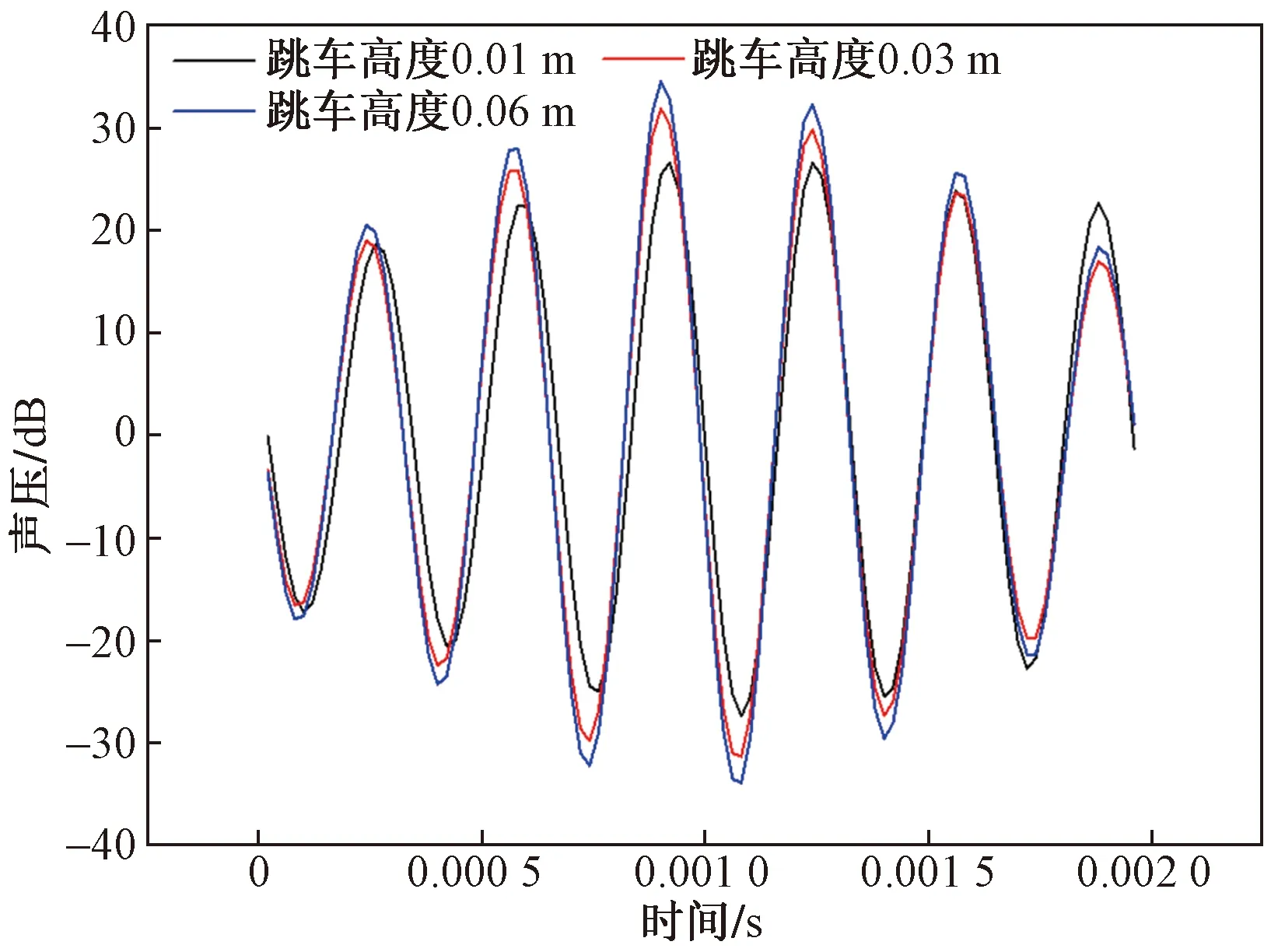
图8 不同跳车高度的损伤伸缩缝麦克风测点3的声压-时间曲线

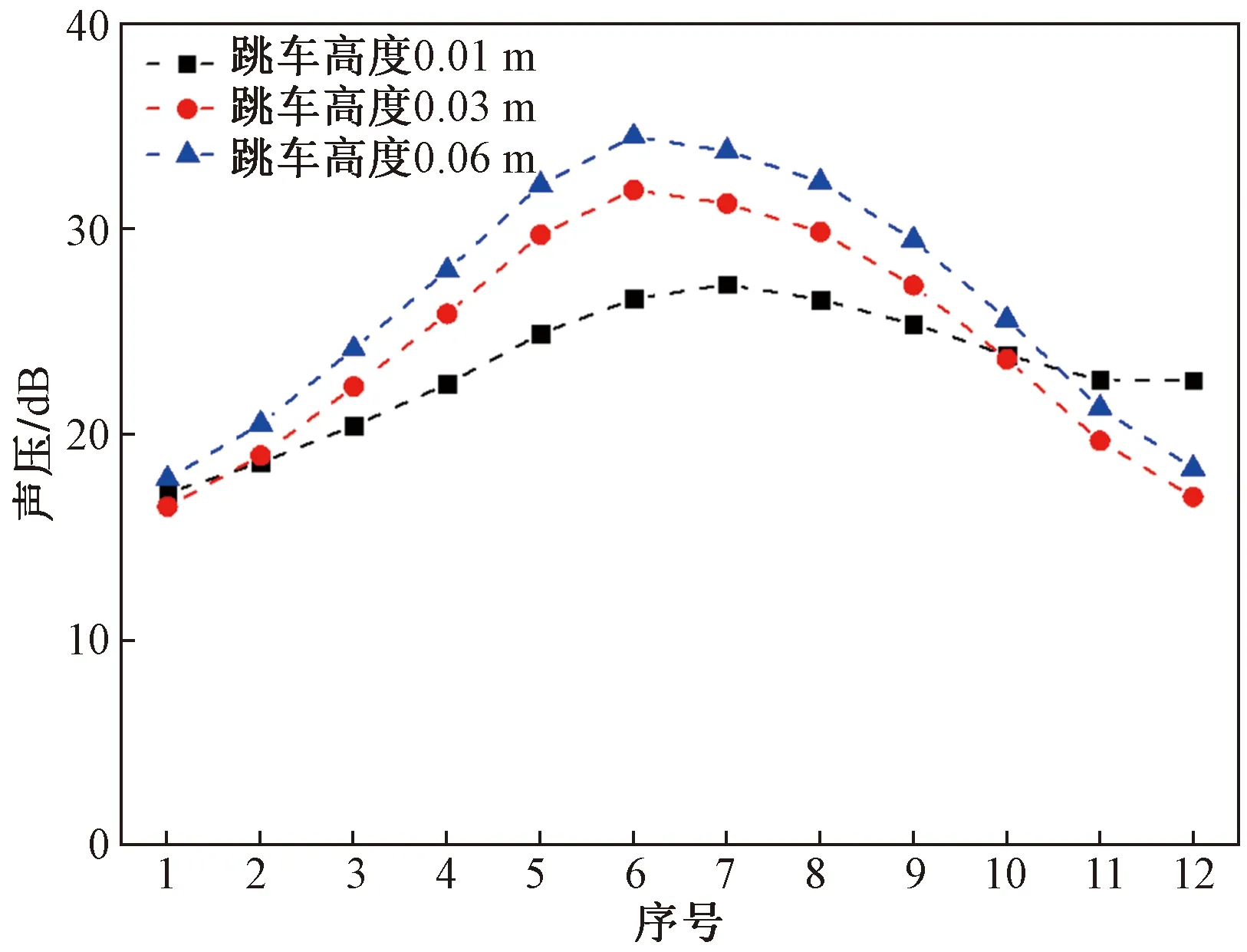
图9 不同跳车高度的声压各波峰波谷绝对值

4 结论

采用动力学仿真得到跳车过程轮胎与伸缩缝接触过程的动力学响应,在此基础上通过声学仿真得到跳车过程产生的噪声声场,分析损伤伸缩缝的噪声特征,研究跳车高度对噪声特征的影响,确定用于伸缩缝健康监测的麦克风布置方案。得到以下结论。

(1) 伸缩缝的健康状态对轮胎与伸缩缝碰撞过程的动力学响应有显著的影响,损伤伸缩缝在跳车过程中的最大应力与最大加速度都大于无损伸缩缝。此外,最大应力与最大加速度都随着跳车高度增加而增大。

(2) 无损与损伤伸缩缝跳车噪声的主要区别是无损伸缩缝的噪声声压远小于损伤伸缩缝,同时无损伸缩缝的声压波形滞后于有损系统。可以利用该特征来识别伸缩缝的健康状态。

(3) 跳车高度会影响系统的声压。跳车高度越高,冲击能量越大,声压越大。麦克风离跳车位置越近,麦克风记录到的声压越大。但是,跳车高度和麦克风位置基本不影响除声压幅值外的声波特征。