考虑劳动力流动限制的供应链网络均衡模型

陈兆波，王 鑫，田春英

(太原科技大学 1.装备制造业创新发展研究中心；2.经济与管理学院，山西 太原 030024)

2020 年3 月11 日，世界卫生组织宣布新冠疫情在全世界范围内开始流行。为了控制疫情扩散，许多国家开始执行疫情期间的隔离政策，以控制新冠肺炎病毒的传播，这严重冲击了劳动力市场的平衡性。例如，疫情发生后我国的劳动力市场发生了巨大的变化[1]，根据人力资源与社会保障部门2020年一季度数据[2]，劳动力市场总体存在需求大于供给的态势，并且劳动力资源在行业间呈现分布不均的情况，其中劳动力市场对各技术等级的用人需求均有所减少，对无技术等级要求的劳动力需求增长了19.2%[3]。新冠疫情造成的劳动力资源短缺以及分布不均等问题[4]，对供应链的生产、运输、储存和分销等活动产生了严重的负面影响。因此，众多企业采取了“共享员工”的措施来缓解劳动力不足的问题，如2020 年3 月，包括餐饮、文娱、零售等行业40 多家企业超3 000 名“共享员工”加入盒马生鲜；美的通过“共享员工”模式派出部分员工支援核心供应商企业，帮助其早日实现复工复产；安徽省合肥市也通过发布《到复工企业就业的倡议书》，鼓励通过“共享员工” 支持企业复工。企业之间相互签订的“共享员工”协议，可以使得劳动力能在同一地区的企业之间自由流动，一方面解决了劳动力匮乏的企业无法生产的问题[5]；另一方面劳动力借出方也可以通过“共享员工”来分担劳动力成本。因此，“共享员工”是疫情防控背景下供应链提升运营效率的有效策略。然而，在供应链竞争背景下，供应链之间的运营策略相互交互，从而使得“共享员工”对供应链的影响还有待探讨。

1 文献综述

在之前的研究中总是假设供应链制造商具有无限产能，然而，现实生活中产能约束在供应链中普遍存在。企业产能受到设备产能不足、原材料短缺等因素的影响。因此，很多学者对产能约束的企业决策进行了深入的研究。例如，Shen 等[6]针对在新产品销售过程中由于产品订单过多造成的产能约束问题，分析动态调整价格措施对产品生产和销售联合决策的影响。张凯等[7]综合考虑网络外部性与价格歧视政策的影响，研究产能约束下寡头垄断产业链中的企业决策问题。Schwarz 等[8]基于确定性周期模型，研究产能不足的企业如何确定单一生产滚动策略与双重销售滚动策略相结合条件的问题。上述文献对供应链参与者的生产能力进行研究，但这些研究对象均集中于单个企业或单条供应链，供应链的结构也主要以一个制造商和一个零售商构成的二级供应链为主。与这些研究不同，本文将在多条异构供应链竞争的背景下，分析“共享员工”对供应链之间的竞争结果的影响。

近年来，国内外众多学者利用变分不等式和均衡理论分析多决策主体构成的供应链系统。例如，Nagurney 等[9]首次提出供应链网络均衡的概念，利用变分不等式确定网络的均衡条件。滕春贤等[10]考虑产品的随机需求性，构建具有随机需求的多商品流供应链网络均衡模型。Zhou 等[11]研究电商双渠道供应链网络，刻画供应链内企业的最优行为与均衡条件。李永华等[12]将保理融资引入供应链网络模型中，分析中小微供应商如何根据电商平台的延期付款期确定保理融资策略。Li 等[13]建立一个供应商和制造商具有产能约束的综合考虑消费者福利和支付意愿以及成本税的多阶段、多层次供应链网络模型，用以评估供应链网络结构对经济、社会和环境可持续性的影响。上述工作的特点是多层多决策者的竞争模型，利用Cournot-Nash 博弈模型和变分不等式求均衡解，但是此类模型一般是由多个制造商、多个分销商和多个零售商构成供应链网络，供应链的结构较为对称。现实中，不同的供应链结构存在极大的差异。因此，研究多条异构供应链构成的供应链系统更具一般性。Chen 等[14]将市场链引入供应链网络，研究在异构供应链网络中供应链管理者在生产水平和资源配置方面的最优决策，并进一步研究在面对需求扰动时供应链网络的最优决策。Feng 等[15]针对贸易政策影响全球供应链网络问题，研究产品市场链在Cournot-Nash 模式下的链间竞争，并进一步分析不同阶段实施的不同贸易政策对供应链网络均衡结果的影响。上述文献研究资源配置、贸易政策等因素对异构供应链的影响，但没有考虑劳动力不足对供应链竞争结果的影响。

经济学概念里劳动力和资本都是生产函数的重要组成部分。在新冠疫情期间，许多企业因缺乏劳动力遭受重大损失，这让一些学者开始关注劳动力对供应链的重要性。Nagurney[16]利用变分不等式，对COVID-19 流行期间美国劳动力资源不足导致生产易腐食品或医疗用品的寡头企业内部供应链网络出现产能约束的问题进行研究，并假设3 种不同的场景来描述劳动力在供应链网络内部的流动模式。研究表明，劳动力的突然中断会降低供应链网络的整体利润，企业应重视供应链网络中的关键链路并保证其有充足的产能。在疫情期间中国实行严格的交通管制措施，为实现复工复产许多企业通过签订“共享员工”协议实现产能互补，由此可见“共享员工”能有效促进劳动力资源整合再分配和提高供应链市场竞争力。

综上所述，本文将针对疫情防控措施导致的不同劳动力流动场景下，分析劳动力资源对供应链网络均衡决策的影响，进一步分析“共享员工”措施在应对劳动力短缺问题中的有效性。特别地，本文将研究置于多条相互竞争的异构供应链的背景下，在不同劳动力流动限制场景下利用变分不等式的方法构建供应链之间相互竞争的均衡模型，通过模型的均衡条件研究“共享员工”策略对供应链运营效率的影响。

2 劳动力约束的供应链网络博弈模型

2.1 模型描述

在针对由M条相互竞争的异构供应链构成的网络模型，供应链m(m=1,···,M)由链内企业和链外企业构成并通过生产、组装、运输、分销、零售等环节将产品销售到终端消费市场n(n=1,···,N) 。假设由不同供应链生产的同质产品在市场上被认为是相同的。对于供应链m而言，与其相关的所有节点企业用集合Am表示，表示供应链m所有内部企业构成的集合，表示供应链m所有外部企业构成的集合，因此Am=。所有企业在空间上分布于J个区域，j=1,···,J，位于地区j的所有企业构成的集合用Aj表示。

本文以一个由两条供应链组成的供应链网络模型作说明，在该模型中包含供应链1 和2 并分别由实线矩形框表示，如图1 所示。

图1 供应链竞争模型Figure 1 A model of inter-supply chain competition

图中的圆圈表示企业节点，供应链1 所有企业构成的集合A1={1,2, 3,4,5,6,7,8,9,10,15,16} ，其中，AI1={6,7,8,9} 为供应链1 的内部企业集合，AO1={1,2,3,4,5,10,15,16}为供应链1 的外部企业集合；供应链2 的所有企业构成的集合A2={1,2,3,4,5,10,11,12,13,14,15,16} ，其中，AI2={11,12,13,14} 为供应链2 的内部企业集合，={1,2,3,4,5,10,15,16} 为供应链2的外部企业集合。用虚线矩形框表示4 个不同的地区节点。位于地区1 的企业构成的集合Aj=1{1,2,3,6} ，位于地区2 的企业构成的集合Aj=2={4,5,11} ，位于地区3 的企业构成的集合Aj=3={7,8,10,12} ，位于地区4 的企业构成的集合Aj=4={9,13,14,15,16} 。企业{10} 为将产品p=6 加工 为 产品p=7 的 第三方企业，企业 { 15,16} 为需求市场。供应链1、2 只产生一种同质最终产品p=9 。

本文借鉴Chen 等[14]提出的市场链的概念，即市场链是为将最终产品送达消费者所从事的特定产品的相关原料获取、生产、组装、配送、销售等内部活动和外部活动所构成的网络，市场链是供应链的一部分。图1 中，企业集合{1,2,3,4,5,6,7,8,9,15}以 及 { 1,2,3,4,5,6,8,9,10,15} 构 成 的 网 络 是 供 应 链1 的两条不同市场链：企业 { 1,2,3,4,5} 负责提供原料p=1,···,5； 企业 { 6} 负责将原料p=1,···,4 组装加工为产品p=6 并运输到下一生产环节；再由企业{7,8}或 { 8,10} 加工组装得到p=7 和p=8 ； 最终在企业{9}加工得到最终商品p=9 ，并运往市 场 { 15} 销售。模型的基本符号如表1 所示，假设所有向量都是列向量，均衡解表示为“*”。

表1 主要参数说明Table 1 Descriptions of main parameters

其中， δaSkm表示企业a是否参加市场链Smk的0-1 变量；是产品生产比例，即市场链上单位流量需要企业a生产的产品数量，以汽车工业为例，若企业a负责生产汽车的车轮，则

假设在每个企业的劳动力投入量都是产品产出的线性函数，因此企业a生产过程中所需劳动力资源量la与产品产出量xa之间的关系为

供应链m的内部企业a的产品流量xa与劳动力成本ha的关系为

外部企业a可以同时参与多个市场链的运营，如企业1、2 等，供应链m从外部企业a(a∈AOm) 处购买材料或者进行产品加工活动。则企业a的利润即为供应链m的生产成本，所以在此引入成本分担机制，将企业a的利润πaSkm(xa) 转嫁到其参与的市场链Skm上，存在

2.2 场景1：受疫情影响劳动力资源无法流动

在场景1 中，由于处于疫情爆发初期，供应链中劳动力出现短缺和分配不均的情况，并且劳动力无法在供应链中流动。在劳动力约束的情况下，供应链m通过决定各市场链流量采取来确保其利润最大，利润函数为Um。

式 (6) 中，第1 项是供应链m的收入；第2 项是供应链m的内部企业运营成本；第3 项是供应链m的材料购入与产品加工生产成本；第4 项是供应链m的总劳动力成本。对 于利 润函 数Um，本 文 假 设 市 场 价 格 函 数 ρSkm单 调递减且连续可微，所有成本函数为凸且连续可微。

式 (7) 由式 (6) 对决策变量X和拉格朗日乘子、分别求偏导再相加得到，变分不等式 (7) 的解则为场景1 下供应链的均衡决策。

2.3 场景2：供应链内部的“共享员工”措施

在场景2 中，假设供应链内部各企业之间短缺的都是对技术等级无要求的普通劳动力，假设是为了让劳动力在供应链内部流动不受岗位因素限制，也符合人力部相关文件要求。供应链管理者对处于同一地区节点j的内部企业的可用劳动力进行统一的协调管理，劳动力资源在同一地区节点的供应链内部企业之间可以任意流动。如图1 所示，供应链1 中处于地区3 的内部企业 { 7, 8} ，供应链2 中处于地区4 的内部企业 { 13, 14} 各自之间可以将劳动力资源统一调动，而其余企业如企业 { 6} 、企业 { 11} 所在地区节点内没有其他属于同一供应链的内部企业，因此无法将劳动力与其他内部企业统一规划使用。

在场景2 中，内部企业的劳动力可用性上限不会超过所在地区节点中所有内部企业的劳动力总数，即

此时供应链优化问题可以表示为

由于可行集 Ω 是紧的且利润函数连续可微，在本文假定的条件下，可以保证变分不等式的解的存在性。

此时式 (10) 的解即为场景2 的均衡解。

2.4 场景3：供应链之间签订“共享员工”协议以应对劳动力约束

在场景3 下，由于疫情防控得力，此时允许同一地区节点的企业之间实行“共享员工”，劳动力能在地区节点j中自由流动，在现实中“美的”在疫情期间就与处于同一地区的上游供应商签订“共享员工”协议助力其恢复生产。企业的利润函数和可行集不仅依赖于其自身的策略也依赖于其他企业的策略。当劳动力资源成为 “共享的”，劳动力约束条件即为“共享约束”。

因此，在场景3 中，供应链网络各企业之间不再是Nash 均衡，而是广义Nash 均衡。同时，考虑到“共享员工”能分担劳动力成本，但也会影响供应链在市场中的竞争力，如何确定“共享员工”在应对劳动力不足问题上的有效性成为需要考虑的问题。

在场景3 中企业a的劳动力可用性上限不会超过所在地区节点j中所有企业的劳动力总数，即对于每个地区节点j，都有

此时供应链的优化问题为

引入关于“共享约束” (11) 的拉格朗日乘子 γj，用 列 向 量 γ 表示所有 γj，存在 γ ∈R+J，定 义 可 行 集。本文利用改进的广义纳什均衡，利用变分均衡定义实现变分不等式的建立。

因为存在“共享约束”，该模型为广义纳什均衡模型，因此变分不等式 (13) 的解即为场景3 的均衡解。

2.5 场景4：后疫情时代供应链是否依然采取“共享员工”

场景4 旨在研究，当疫情被有效控制住后，劳动力可以在不同地区节点间任意流动，在不引入新的劳动力资源情况下，企业是否继续采取“共享员工”策略来保证自身的利润最大。这也是目前劳动力市场面临的实际问题——“共享员工”是否能在后疫情时代继续延续？

同场景3 类似，场景4 各供应链之间存在共同劳动力总数约束，故也是广义纳什均衡。在场景4 中企业a的劳动力可用上限不会超过系统中所有企业的劳动力总数，即

引入关于“共享约束” (14) 的拉格朗日乘子 τm，用列向量 τ 表示所有 τm，存在 τ ∈R+M，定义可行集，此时供应链的优化问题为

同场景3 建立变分不等式：

类似场景3，变分不等式 (16) 的解即为场景4 的均衡解。

3 算法模型

参照文献[12]，给出求解问题 (7) 的方法，式(10) 、式 (13) 、式 (16) 解法同式 (7)。令

则变分不等式问题 (7) 可转化为标准形式，寻找 Φ*∈Θ ，使得其满足

本文运用Matlab2019b 软件对上述例子进行求解，下面给出Eluer 算法的具体步骤。

4 数值算例

在本节中，将给出几个数值例子来说明这个模型，为计算方便算例不考虑量纲。

表2 为企业a生产比例，若企业a参与市场链，则有一特定值；否则，该值将毫无意义，用 “—”表示。表3 给出企业a劳动力产出率ga，即生产单位产品所需人工和企业a在疫情初期受到影响时所拥有的劳动力数量。

表2 产品生产比例Table 2 Proportions of production

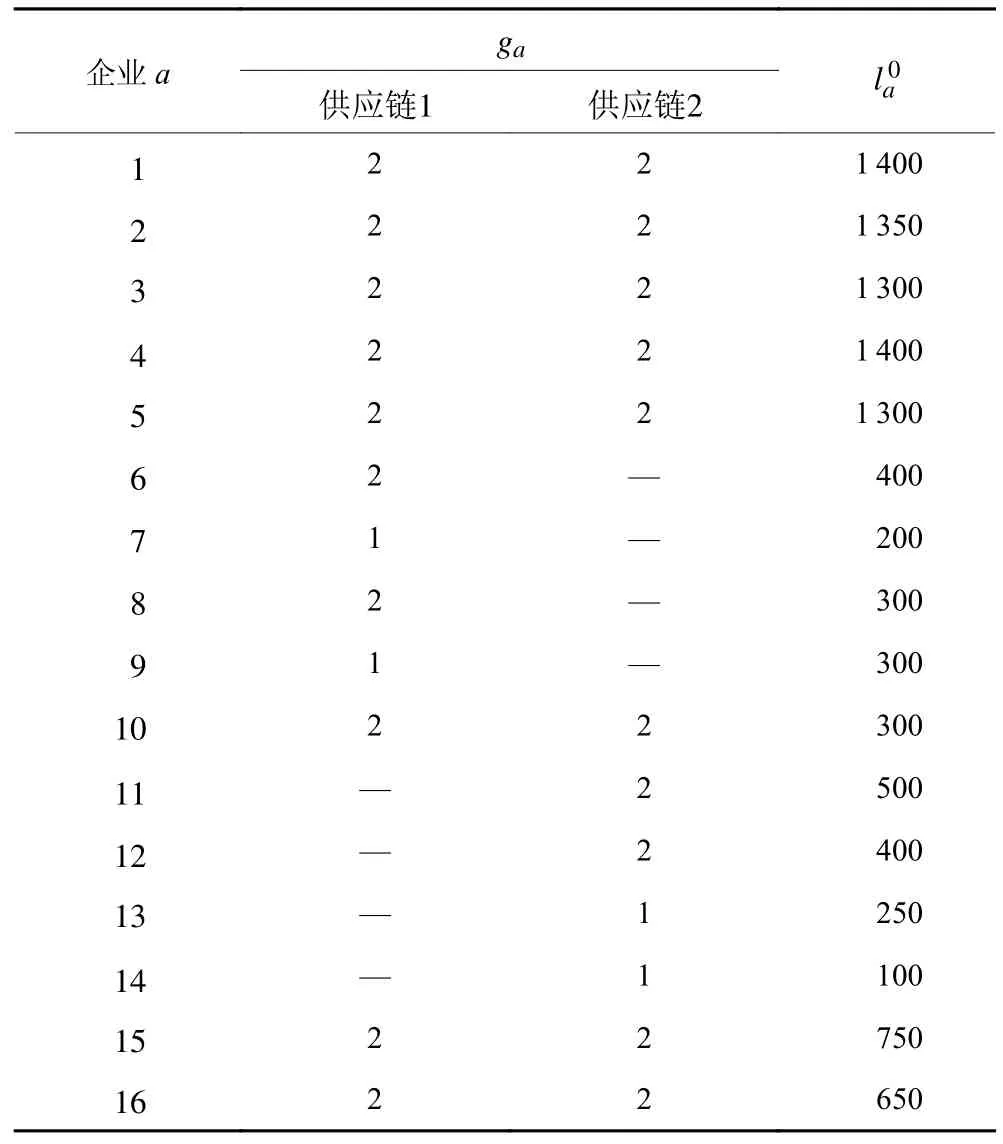
表3 劳动力产出率及劳动力数量Table 3 Labor output ratios and the number of labors

如图1 所示，有两条竞争的供应链，都生产同一 种 产 品p=9 。外 部 企 业 { 1,2,3,4,5} 是 这 两 条 供 应链的原材料供应商，第三方企业{10}负责将投入产品p= 6 转化为产出产品p= 7，企业 { 15,16} 为需求市场。

假设这些外部企业的运营成本函数为

内部企业的运营成本函数为

为方便分析，设定企业a支付给员工的计件报酬均为=5 ，基本报酬均为c2la=1 ，a∈Am。

S11、S21、S13、S41是属于供应链1 的市场链，它们分别由以下几组企业组成：

需求市场上产品p=9 的价格函数为

4.1 劳动力资源对供应链网络均衡结果的影响

本节从劳动力资源角度出发，选择在每个场景中都参与了流动的企业 {8} 作为研究对象，并设定企业 { 8} 拥有不同数量的劳动力资源。

4.1.1 劳动力数量对供应链网络的影响

设定企业 {8} 拥有不同数量的劳动力资源，劳动力数量变化以100 为步长，劳动力数量范围为 [100,1 700]。

1) 观察图2 可知，随着企业 { 8} 劳动力资源数量增加，供应链1、2 总体产量增加。由于供应链生产流程衔接紧密，单个环节产量受其他生产环节影响。在场景1、2 中，当企业 { 10} 在l10=300 处达到产能上限时，供应链1 产量在l80=400 处达到峰值，此时供应链网络总产量会在l80=400 处停滞不前。同理在场景3 中，当地区节点Aj=2处劳动力达到上限，供应链总产量在l80= 1 500 处最高。若此时继续增加企业 {8} 劳动力数量，一方面会导致供应链网络产量升高、产品市场价格下降，如图2、图3 所示；另一方面企业 {8} 持有劳动力的成本上升，使得“共享员工”策略失效。因此，采取“共享员工”措施缓解产能约束不能只局限于单一环节，应从整体出发综合考虑。

图2 劳动力数量变化对供应链产量影响Figure 2 The impact of supply chain outputs on labor variation

图3 企业8 劳动力数量变化对市场价格的影响Figure 3 The impact of labor variations in firm 8 on market prices

2) 结合图2、图4 可知，在场景2 中，当供应链内部采用“共享员工”后，对于供应链1，企业{7,8}将劳动力资源统一规划使用后缓解了产能不足问题，增加供应链1 市场竞争力。对于供应链2，产能约束在整合企业 { 12,13} 劳动力资源后仍存在，原因是无法生产核心部件p=7 ，只能依赖于外部企业 { 10} 。供 应 链1 竞 争 加 强和企业 { 10} 产能不足导致供应链2 产量降低、市场竞争力下降。因此采用“共享员工”需要综合考虑企业产能结构，当该生产环节没有劳动力约束时，贸然采用“共享员工”是无效的。

图4 企业8 劳动力数量变化对供应链利润的影响Figure 4 The impact of labor variations in firm 8 on supply chain profits

3) 在场景4 中疫情防控得当，劳动力流动限制程度最低。从图2、图4 可以看出，此场景中供应链1、2 的产量、利润均高于其他场景，这是因为企业通过“共享员工”策略可以很好地根据自身产业结构调整劳动力资源配置优化劳动力成本。

4.1.2 劳动力流动模式对供应链网络的影响

故本节在4.1.1 节基础上，研究不同劳动力流动模式下核心企业 { 10} 产能不足对供应链决策的影响。

1) 结合图2、图4 和图5 可知，在供应链整体处于产能分布不均的场景1、2 中，由于供应链2 不具备生产核心部件p= 7 的能力，劳动力流动限制条件对供应链2 的影响较供应链1 更大，此时供应链2 采用“共享员工”措施对缓解生产压力无效；当劳动力流动程度上升，由于场景3 允许劳动力在同一地区节点内流动，供应链中企业{12}会倾向于向产能不足的企业{10}“共享”劳动力，可以看出作为合作方的供应链内外部企业之间，在对方面临产能不足时，为了不影响自身经营状况，会采取“共享员工”的举措，帮助合作伙伴度过困境，实现共赢。

图5 企业 10 劳动力数量变化Figure 5 Labor variations in firm 10

2) 由图5 可知，在劳动力流动限制最低的场景4 中，“共享员工”措施让企业 { 10} 劳动力充足，由于供应链2 生产成本较供应链1 更低，因此能在产量低于供应链1 的情况下获得更高利润；但对于供应链1，“共享员工”使得其劳动力资源被共享给整个供应链系统，随着企业 {8} 劳动力增加导致市场价格降低，在l08= 1 500 之后，场景4 中供应链1 的收益低于在场景3 中的收益，此时“共享员工”降低了供应链1 的运营效率。

4.2 “共享员工”对供应链系统运营的有效性

本节将分析“共享员工”策略对供应链系统运营效率的影响。假定供应链1 企业 {8} 拥有充足的、不同 数 量 的 劳 动 力 资 源，在 [400,1 000] 区 间 内 以100 为步长变化；同时供应链2 内部企业 { 12} 发生劳动力中断=0 ，其余参数同4.1 节。本节算例将针对供应链1 在场景1 和场景3 中的运营情况，研究“共享员工”对供应链系统运营的有效性。根据第2 节算法，计算得供应链的均衡产量、市场价格及利润见图6 ～ 8。

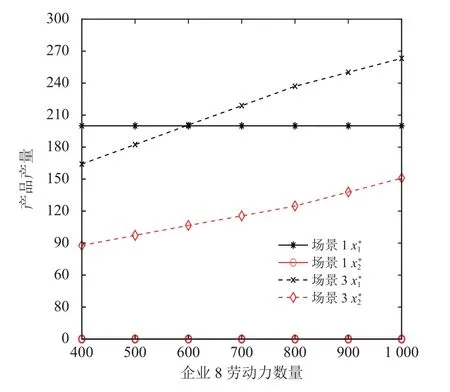
图6 供应链产量变化Figure 6 Variations of supply chain output

图7 市场价格变化Figure 7 Variations of market prices

由图6 ～ 8 均衡结果，得到下列结论。

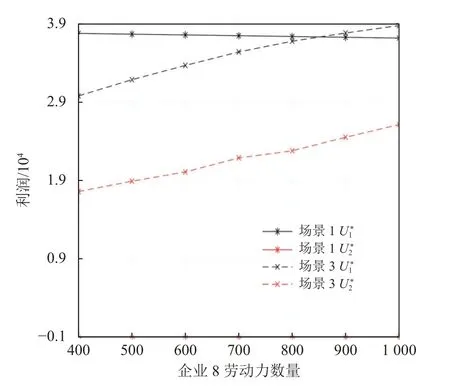
图8 利润变化Figure 8 Variations of profits

2) 结合图6 ～ 8 均衡结果可知，在场景3 允许劳动力在同一地区节点间自由流动的情况下，供应链1 与供应链2、链外企业分别签订“共享员工”协议。供应链1 采取“共享员工”后，企业 { 8} 劳动力流向企业 { 10、12} ， 在 区间 [400,600] 内，供应链1 产量低于场景1 不采取“共享员工”时，并且由于供应链2 的产品输出量增加，从而导致产品市场价格下降，因此供应商 1 的产品输出量和利润降低；在区间[600,800] 内，随着企业 { 8} 劳动力增加，场景3 中供应链1 产量上升并高于场景1 中产量，但由于供应链2 的产品输出量增加，从而导致产品市场价格下降，此时供应商 1 的利润低于场景1。可以看出，在供应链竞争背景下，上述情况中“共享员工”损害了供应链1 的利润。

5 结束语

本文将劳动力引入供应链网络，利用变分不等式的方法构建考虑劳动力流动限制的供应链网络均衡模型，分析了劳动力资源及流动模式对供应链网络均衡决策的影响，进一步分析“共享员工”策略对供应链运营效率的影响，并用欧拉算法做了一些数值算例。结果表明: 1) 对于劳动密集型企业而言，劳动力资源不足会降低供应链的产量及利润，且由于供应链生产流程前后衔接紧密，故单个环节产能不足会降低供应链总产量；2) “共享员工”可以帮助供应链根据自身产业结构及需求更好地分配有限的劳动力；3) 作为合作方的供应链内外部企业之间，在对方面临产能不足时，为了不影响自身的经营状况，会采取“共享员工”的举措； 4) “共享员工”在某些情况下会损害供应链的利益。

本文主要考虑劳动力流动限制带来的供应链产能约束问题，未来可以将研究扩展到通过智能制造方面，具体是通过投入生产效率更高的自动化设备提高减少人工以应对劳动力不足情况。