多尺度点-线目标拓扑关系不一致性探测方法
温伯威,李少梅,姚诚勤
1. 信息工程大学 地理空间信息学院,郑州 450001;
2. 61175 部队,南京 210049
1 引 言
拓扑关系在人类依据地图认知客观地理环境的过程中发挥着重要作用,依据拓扑关系认知地理空间环境是人类的本能。拓扑关系不一致性是同一地理实体集之间的拓扑关系在地理空间数据表达中存在矛盾和冲突。依据表现形式的不同,拓扑关系不一致性可以分为三类,分别是单一尺度数据集中同类要素之间的拓扑关系不一致性、同一数据集中不同要素类目标之间的拓扑关系不一致性、不同尺度数据集中同名目标之间的拓扑关系不一致性。拓扑关系不一致不仅违背了客观世界中地物之间的真实空间关系,而且会造成查询与分析结果的错误(杜世宏等,2015)。现有生产作业环节中主要依靠作业员采用人工方式发现并处理点-线目标之间的拓扑关系不一致性,不仅效率低,而且依赖作业员的经验。因此,不一致性探测对提高多尺度点-线目标拓扑关系一致性处理的科学性和效率具有十分重要的意义。
鉴于拓扑关系在空间分析与地理空间环境认知中的重要地位和作用,大量研究围绕系列比例尺地图生产与更新(张新长等,2021;李靖涵等,2017;周明辉和翟仁健,2017)、多源地理空间数据集成与融合(孙群等,2022;马京振等,2022;唐忠成等,2021)、地理空间数据质量控制中的拓扑关系不一致性(李文德,2021;郑衡和周晓光,2020;陈楠和张标,2020;Zhang 等,2021)等展开。已有研究主要集中在单一尺度数据集中同类要素之间的拓扑关系不一致性检测与处理、同一数据集中不同要素类目标之间的拓扑关系不一致性检测和处理方面。
单一尺度数据集中同类要素之间的拓扑关系不一致性,又称为拓扑错误,是数据表达违背完整性约束造成的空间目标与客观现实的矛盾问题,如面目标不闭合、悬挂点、目标重复、相邻多边形共享边界不重合等。利用拓扑关系约束规则检测单一尺度数据集中同类要素之间的不一致性是已有研究通常采用的方法(Liu 等,2005;Brisaboa 等,2014;周凯等,2018)。
同一数据集中不同要素类目标之间的拓扑关系不一致性,又称为拓扑语义冲突,是数据表达违背语义约束造成的空间目标之间拓扑关系的不合理问题,如居民地落水、河流走向偏离山谷线(河曲矛盾)、高程点与相邻两等高线的高程值矛盾(高曲矛盾)、同一等高线与河流在小范围内多次相交等。现实世界中地理实体之间的关系遵循一定的地学规律,将现实世界中地理实体之间的约束关系映射成空间数据库中合理的空间关系,依据这些合理的空间关系制定空间冲突判断规则,利用规则识别不同地理实体之间的空间冲突,是拓扑语义冲突检测研究最常用的方法(张旗升等,2019;康顺等,2019;杨敏等,2020)。同一尺度数据集中不同要素类之间的拓扑关系不一致性研究成果主要包括河流与等高线(刘万增等,2008;李国辉等,2014;李振豪等,2018)、居民地与道路(郑春燕和胡华科,2012;Liu 等,2014)、居民地与河流(郭庆胜等,2018;李靖涵,2015)之间拓扑关系不一致性的探测和处理方法。
不同尺度数据集中同名目标之间的拓扑关系不一致性,是同名地理实体之间的拓扑关系在不同尺度数据集表达中存在着矛盾和冲突。例如,在大比例尺地图数据中河流与居民地之间的拓扑关系是相离,在小比例尺地图数据中两者之间的拓扑关系被表达成相交关系,显然,同名目标之间的拓扑关系在不同尺度数据表达中存在着矛盾。从河流与居民地两者之间的拓扑关系的语义约束来看,相离、相交、相切都是合理的,因此,在单一尺度数据质量检测中河流与居民地在现实世界中的相离关系,表达成数据库中相交关系可能被误认为是合理的。因此,检测这类拓扑关系不一致性需要参照相邻大比例尺数据中地理实体之间的拓扑关系。
道路和居民地作为基础地理空间数据中两类最重要的地图要素,两类要素之间拓扑关系表达的准确性直接影响着用户能否通过地图获得对现实世界正确的空间认知。受制图综合、符号尺寸、比例尺等因素的影响,不同尺度地理空间数据中同名点状居民地与线状道路之间的拓扑关系不一致性问题十分突出。本文以同名点状居民地与线状道路为例,研究了多尺度点-线目标的拓扑关系不一致性问题,提出了基于拓扑距离的多尺度点-线目标拓扑关系不一致性探测方法。
2 多尺度点-线目标拓扑关系不一致性探测方法
科学、合理的拓扑关系形式化描述方法,是进行多尺度点-线目标拓扑关系不一致性探测的基础和前提。九交模型作为一种拓扑关系形式化表达模型,能够有效区分点-线目标之间的三种拓扑关系(汤鑫,2021)。拓扑距离是度量九交模型值差异的常用方法。拓扑距离越大,同名点-线目标之间的拓扑关系差异越大;当拓扑距离为零时,同名点-线目标之间的拓扑关系在不同尺度数据中相同。研究以点状居民地与线状道路为例,利用拓扑距离描述不同尺度数据中同名点状居民地与线状道路之间的拓扑关系差异。
多尺度点-线目标拓扑关系不一致性探测的技术路线,如图1 所示。第一,将两种不同尺度的地图数据进行叠置;第二,通过多尺度同名实体匹配,分别建立不同尺度数据中点状居民地与点状居民地、线状道路与线状道路之间的匹配关系,为拓扑关系不一致性探测提供研究对象;第三,依次计算同名点状居民地与同一线状道路的拓扑关系,采用九交矩阵记录点状居民地与线状道路之间的拓扑关系;第四,计算同名点状居民地与同一线状道路之间的拓扑距离,通过判断拓扑距离是否为零,进而确定不同尺度数据中同名点状居民地与同一线状道路之间的拓扑关系是否一致,直至所有对象探测完毕。
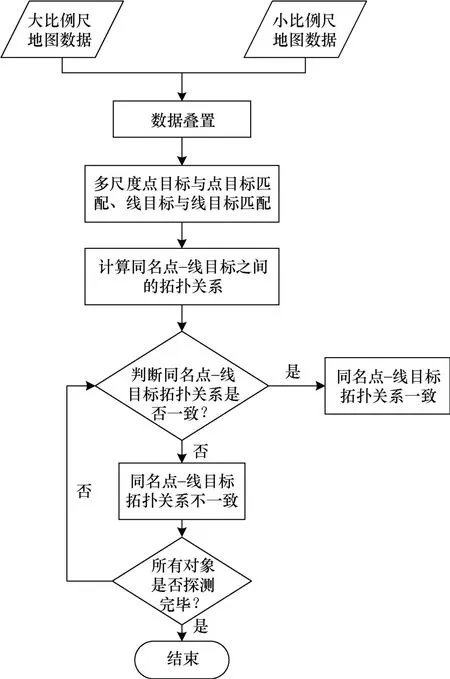
图1 多尺度点-线目标拓扑关系不一致性探测技术路线Fig.1 Multi-scale point-line object topological inconsistency technology roadmap
2.1 多尺度点-点目标及线-线目标匹配关系的建立
由于现实世界中的居民地通常沿主要道路分布,所以在多尺度地图数据表达中同名点状居民地通常位于同一线状道路的邻域范围内。同一线状道路邻域范围内可能会有多对同名点状居民地,位于同一线状道路邻域范围内的同名点状居民地与该线状道路之间拓扑关系在不同尺度地图数据表达中可能存在不一致,不在同一线状道路邻域范围内的同名点状居民地与该线状道路之间拓扑关系都是相离,不存在拓扑关系不一致。由此可以看出,在多尺度点-线目标拓扑关系不一致性探测过程中,考察的对象是不同尺度数据中的同一线状道路和位于同一线状道路邻域范围内的同名点状居民地。因此,研究采取如下策略建立不同尺度数据中线状道路与线状道路、点状居民地与点状居民地的匹配关系。
首先,利用结点相似度与弧段方向相似度计算参考线状道路和待匹配线状道路之间的相似性,当两者之间的相似度大于阈值时即可判定为同名线状道路。
其次,以同名线状道路为基础,计算其邻域范围内的同名点状居民地,并建立同名线状道路与其邻域内同名点状居民地之间的联系。
设iL为小比例尺数据中的线状道路,iL′为大比例尺数据中iL的同名线状道路。同名线状道路iL与iL′邻域范围内同名点状居民地的判定步骤如下:
(1)以Li为中心、δbuffer为半径构建缓冲区Rbuffer,以Rbuffer作为Li的邻域;
(2)依次搜索小比例尺数据中位于缓冲区Rbuffer中的点状居民地hi,将hi加入集合H={h1,h2, …,hi};
(3)在大比例尺数据中依次提取hi的同名点状居民地hi′,将hi′加入集合H′ = {h1′ ,h2′ , …,hi′}。
2.2 拓扑距离的计算
矢量空间中,点目标与线目标之间的拓扑关系包括三种,分别是相离(点不在线上)、相接(点在线边界上)、包含(点在线内部)。相离、相接、包含分别对应着具有不同元素值的九交矩阵,它们之间的差异可以通过拓扑距离计算。设P、P′为点目标,L、L′为线目标,P与L之间的拓扑关系为R1,P′与L′之间的拓扑关系为R2,R1与R2对应的九交矩阵分别为M1与M2,R1与R2之间的差异可以通过拓扑距离度量,拓扑距离的定义如下:
式中,DR1R2为R1与R2之间的拓扑距离;i、j分别为矩阵M1与M2的行号和列号。
采用式(1)分别计算相离、相接、包含三种关系两两之间的拓扑距离,如表1 所示。两种相同拓扑关系之间的拓扑距离为零,相离与相接、相离与包含、相接与包含之间的拓扑距离都为4。
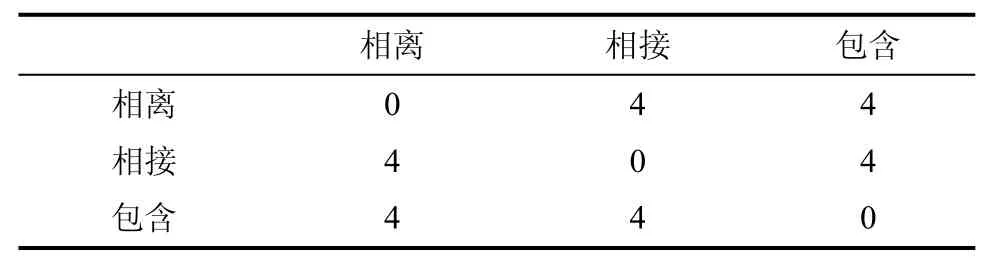
表1 相离、相接、包含两两之间的拓扑距离Tab.1 Topological distances between disjoint, adjacent,and containing pairs
2.3 点-线拓扑关系的判断方法
地图空间中,设h为点状居民地,Oh为h的中心点,R h为点状居民地符号的半径,L为线状道路,l为L的中心线,Lwidth为线状道路符号的宽度。其中,l由一系列首尾相连接的直线段si组成,即l= {s1,s2,… ,si},Pstart、Pend分别为l的起始点和终点,D(Pstart,Oh)、D(Pend,Oh)分别为Pstart、Pend与Oh之间的距离,MhL为Oh与l之间九交矩阵的值,研究采用九位二进制数字记录九交矩阵中的各个元素值。
点状居民地与线状道路之间的拓扑关系可以通过计算hO与l之间的距离d判断。由于数字地图生产与作业规范中要素最小线宽为0.1 mm,所以取0.1 mm 作为判断点状居民地与线状道路相切、相交、包含的阈值。由于矢量空间中的相离关系与地图空间中的相离和相切都等价,因此,必须依据点状居民地符号边缘与线状居民地符号边缘之间的距离1d对矢量空间中的相离进行区分:
地图空间中,为了区分点状居民地与线状道路之间的拓扑关系,定义如下判断规则:
规则1:若10.2d> ,则在地图空间中的点状居民地与线状道路相离,在矢量空间中MhL=001001111,标记为第I 类相离;
规则2:若 0 ≤d1≤ 0.2,则在地图空间中的点状居民地与线状道路相切,在矢量空间中MhL=001001111,标记为第II 类相离;
规则3:若0 ≤d<0.1,D(Pstart,Oh) -Rh>0.1且D(Pend,Oh) -Rh> 0.1,则在地图空间中的点状居民地在线状道路内部,在矢量空间中,MhL=111001001;
规 则 4 : 若0 ≤d<0.1, 0 <D(Pstart,Oh)-Rh< 0.1或0 <D(Pend,Oh)-Rh< 0.1,则在地图空间中的点状居民地在线状道路边界上,在矢量空间中,MhL=111001001。
在判断点状居民地与线状道路拓扑关系的过程中,计算Oh与l之间的距离d是关键。O h与l之间距离的实质是点到折线之间的距离,其定义如下:点到折线的组成线段之间距离的最小值,d为以Oh(x0,y0)为圆心且与线段si相切圆的半径,如图2 所示。
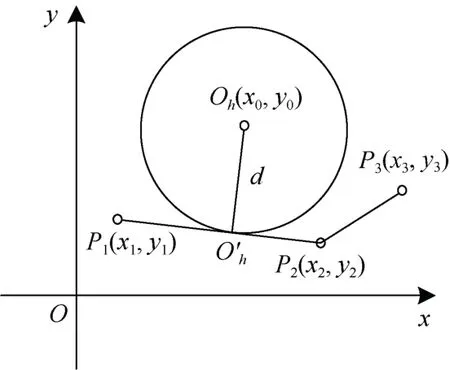
图2 点到折线之间距离的定义Fig.2 Definition of distance between points and polyline
根据Oh沿线段si方向的投影点是否在si上,计算Oh到线段si之间的距离分为三种情况。判断Oh沿线段si方向的投影点是否在si上的方法为,设Oh′为Oh在si上的投影点,u为点P1到点Oh的向量,记u=,v为点P1到点P2的向量,记v=,m为点P1到点Oh′的向量,记m=,根据解析几何原理:
2.4 多尺度点-线目标拓扑关系不一致性探测算法
多尺度地图数据中,同名点状居民地与同一线状道路之间拓扑关系不一致性的探测算法如下所述。
(1)以小比例尺数据中的线状道路Li作为参考数据,在大比例尺数据中搜索Li的同名线状道路Li′,构建不同尺度数据中同名线状道路集合M={(L1,L1′),(L2,L2′), …, (Li,Li′)}。
(2)以同名线状道路Li、Li′为基础,构建其邻域范围内同名点状居民地集合Ni={(h1,h1′),(h2,h2′), …, (hk,hk′)}。
(3)依次判断hk与Li、hk′与Li′之间的拓扑关系Ri、Ri′,分别得到hk与Li、hk′与Li′之间九交矩阵为Mi、Mi′,当为相离关系时,依据规则1 和规则2 记录相离的类型。
(4)采用式(1)计算Ri与Ri′之间的拓扑距离。判断Ri与Ri′是否一致:若= 0,Mi≠001001111且≠001001111,则Ri与一致;若=0,Mi= 001001111且Mi′= 001001111,且相离类型相同,则Ri与Ri′一致,反之,Ri与Ri′不一致。
3 实验验证与分析
采用同一地区不同尺度(1∶25 万、1∶50 万)的国道、省道、点状居民地数据作为实验数据,验证多尺度点-线目标拓扑关系不一致性探测方法的正确性和适用性。1∶25 万数据包含的线状道路(国道与省道)、点状居民地的个数分别为45、1906,1∶50 万数据包含的线状道路(国道与省道)、点状居民地的个数分别为44、526,拓扑关系存在不一致性的同名点状居民地与同名线状道路共有9 对。部分同名省道与邻域内同名点状居民地之间拓扑关系不一致性探测结果,如表2 所示。
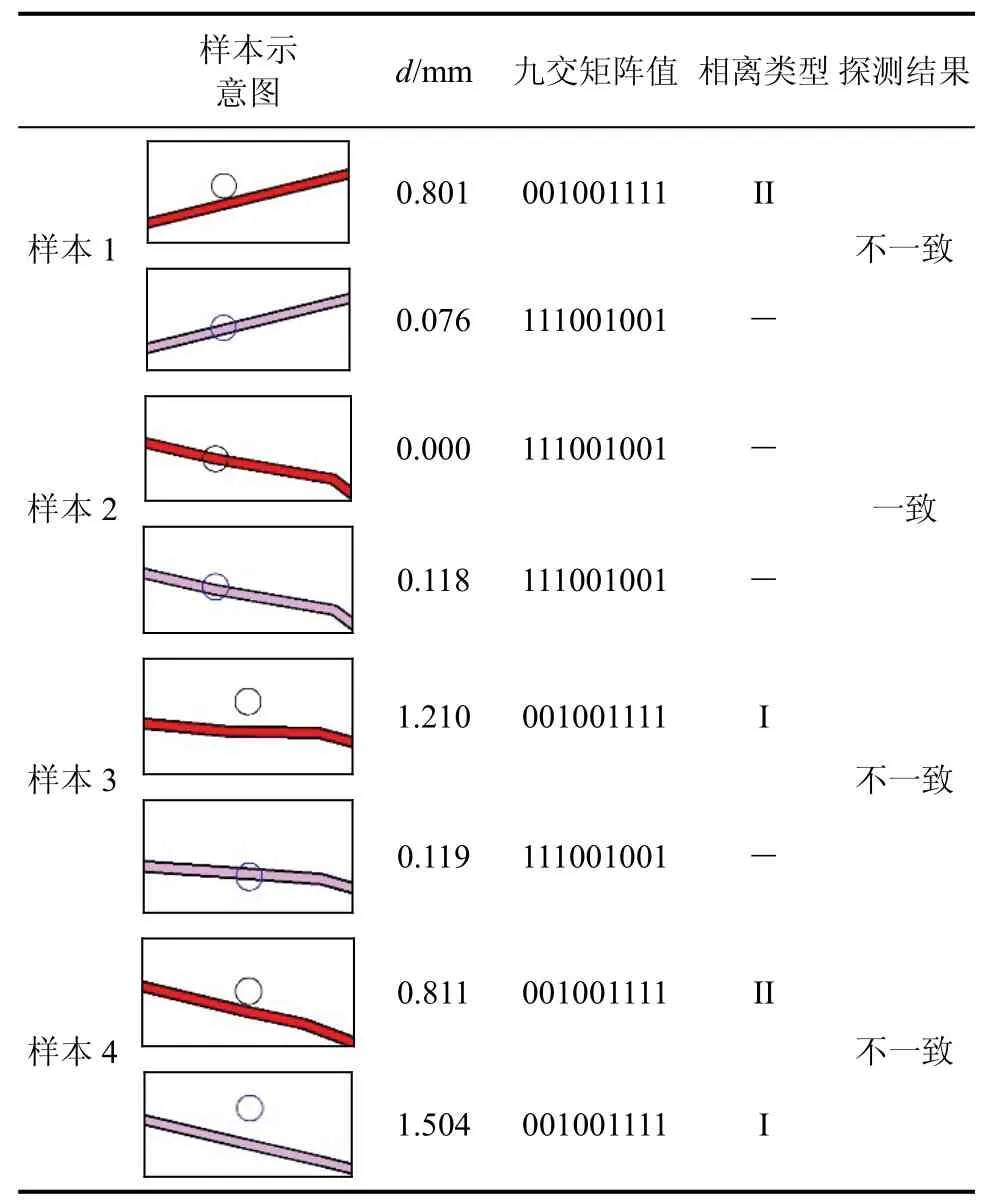
表2 拓扑关系不一致性探测结果(部分)Tab.2 Topology inconsistency detection results (part)
根据1∶25 万地图规范和图式,点状居民地符号的半径为0.55 mm,省道符号的宽度为0.5 mm。因此,当点状居民地符号定位点与省道符号定位线之间的图上距离 1mmd> 时,点状居民地与省道之间的拓扑关系为相离;0.8 1d≤ ≤ 时,点状居民地与省道之间的拓扑关系为相切;0 0.8d<≤ 时,点状居民地与省道之间的拓扑关系为相交。由表2中,同名省道与邻域内同名点状居民地之间拓扑关系不一致性探测结果,可以得到:①由于不同尺度数据中点状居民地符号与线状道路符号的尺寸保持不变,大比例尺数据中点状居民地与道路之间的拓扑关系随着比例尺变小发生变化,如样本1 中两者之间的拓扑关系由相切变成相交,样本3 是由相离变成相交;②基于九交模型探测不同尺度数据中点-线目标拓扑关系不一致性的结果与人工判断结果一致。
4 结 论
“互联网+”和大数据时代的到来,爆炸式增长的海量多源多尺度地理空间数据之间的拓扑关系不一致性问题,给地理空间数据协同应用带来了新挑战。本文以同名点状居民地和线状道路之间的拓扑关系不一致性为例,提出了利用拓扑距离的多尺度点-线目标拓扑关系不一致性探测方法,并进行了实验分析。研究表明,探测结果可以作为不同尺度地理空间数据中点-线目标拓扑关系一致性处理的依据。

